大倾角煤层时深转换精度分析及改进方法

王惠风，符 超,3，李 果，陈同俊

(1.国能神东煤炭集团有限责任公司，陕西 神木 719315；2.中国矿业大学 煤层气资源与成藏过程教育部重点实验室，江苏 徐州 221008；3.中国矿业大学 资源与地球科学学院，江苏 徐州 221116)

由于国家政策要求和企业发展需要，智能化开采是煤炭安全高效开采的发展方向和必然趋势[1]。中华人民共和国国家发展和改革委员会于2020 年下发的《关于加快煤矿智能化发展的指导意见》指出，大型煤矿和灾害严重煤矿2025 年前要基本实现开采智能化，各类煤矿2035 年前要基本实现开采智能化[2]。有效地质保障是智能化开采基础，高精度预测煤层底板高程是实现透明工作面和智能化开采的关键之一。现有资料表明，在勘探阶段，煤层底板高程解释误差较大，很难满足智能化开采的高要求[2-4]。

地震勘探是煤田勘探的主要技术手段之一，在煤田构造解释中发挥着重要作用。特别是三维地震技术在煤田大范围应用后，极大地提高了煤田构造解释的精度和可靠性[5]。近年来，高密度三维、五维插值、炮检距向量片、叠前偏移等技术的相继推广，使复杂采区的构造解释精度得到了进一步的提高[6-10]。相对于测井来说，地震勘探虽然纵向分辨率不足，但空间采样率高、横向连续性好。将两者有机结合，可以获得更好的勘探效果[11]。

对于未开展深度偏移的地震勘探资料来说，为时间域成果，不能直接和煤层底板高程相对应。在利用地震勘探成果时，如何实现其高精度的时深转换，精准预测煤层底板起伏与倾角变化，对矿井智能化开采尤为关键[2]。当探区钻孔较少、构造较简单时，基于多项式或幂函数拟合的常速时深转换方法效果较优[12-14]。当探区钻孔较多、构造较简单时，基于反距离加权或克里金法的空间插值法最为常用[15]。当探区地质构造较复杂时，地质构造和叠加速度场控制的变速成图效果较优[16-18]。对于煤矿采区来说，利用巷道揭露的见煤点数据，动态解释煤层底板高程，精度更高[19]。

虽然业界已对地震资料时深转换开展了较深入的研究，但对于插值方法优选和插值参数影响的研究还不够深入。本次分析大倾角单斜煤层模型和实际三维采区数据，分析多种插值方法对平均速度插值精度的影响，对提高煤田地震资料时深转换精度具有明显的理论意义和应用价值。

1 理论方法

1.1 平均速度法

平均速度法是煤田地震勘探时深转换的最主要方法，在二维地震勘探和三维地震勘探中获得了大量应用[4,16]。对于钻孔揭露的控制点，第i个地层，其厚度为Hi，双程旅行时为ti，则第N层的平均速度vN可表示为[20]：

依据控制点处平均速度，插值生成所有共中心点的平均速度，即可实现煤层层位时间的时深转换。

1.2 插值方法

由于插值生成的平均速度精度决定了时深转换精度，插值方法的选择至关重要。本次以多项式、克里金和回归型支持向量机等方法为例，分析平均速度插值精度及改进方法。

1)多项式插值

多项式拟合是最常用的插值方法，点x处的平均速度v(x)[21]可表示为：

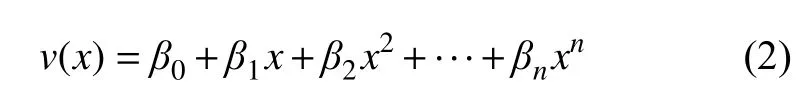
式中：β0,β1,···,βn为系数；n为多项式的项数。

以已知点为控制点，通过最小二乘法，拟合所有系数，即可获得平均速度的数学表达式。

2)克里金插值

克里金(Kriging)插值方法，是时深转换中应用最广泛的方法之一[16,22]。在空间相关范围分析的基础上，用相关范围内的采样点属性值估计待插值点属性值[22-23]。对待估计点x处的速度值v*(x)，可表示为：

式中：λi为空间距离相关系数；v(xi)为相关范围内的采样点速度值；xi为插值点位置。

3)回归型支持向量机

回归型支持向量机(Regression Support Vector Machine，RSVM)是一种常用的机器学习回归预测模型，由于具有解全局最优的特性，被广泛应用于工程数据回归分析中[24]。其通过变换将训练集{(Xi,yi),i=1,2,···,l}映射到高维特征空间，并构造线性回归函数求解，可表示为[24-25]：

式中：W为可调的权值向量；φ(X)为非线性映射函数；b为常数。

2 速度模型建立

现有研究表明，当地层较平坦、横向速度变化较平缓时，平均速度法的精度较高[4,16]。但当地层倾角较大、横向速度变化较快时，平均速度法的精度明显受限。为了研究平均速度法的时深转换精度及改进方法，参照大倾角采区煤层分布特征，建立横向速度快速变化的层速度模型，如图1a 所示。其中，浅部是厚度为100 m 的第四系低速层，其下是大倾角单斜地层。煤层厚度为5 m，层速度为2.2 km/s，位于3.6 km/s 高速基岩层之上，是本次研究的目标地层。

以原始速度模型和平滑处理后的层速度分布(图1b)为输入，分别计算其平均速度分布，如图1c和图1 d 所示。总体来说，模型平滑处理前后的平均速度分布形态相似，呈凹槽形，与所建立模型的速度分布特征一致。求取平滑处理前后模型的平均速度差，如图2 所示。其中，速度差异显著，最大差异达0.3 km/s，满足研究时的差异性要求。

图1 模型平滑前后的层速度和平均速度Fig.1 Interval and average velocities before and after smooth operation

图2 模型平滑前后平均速度之差Fig.2 Velocity difference before and after smooth operation

3 控制点直接插值效果对比

在煤田地震勘探中，工区内通常有一定数量的钻孔和巷道揭露的见煤点。其中，钻孔网格密度最高可达0.5 km×0.5 km，而见煤点的密度更高。以实际揭露的煤层底板高程为控制点，插值生成目标煤层平均速度，进而实现地震资料的时深转换是最常用方法。本次结合多项式插值和克里金插值等算法，深入研究平均速度插值效果。

为了检验多项式法和克里金法的内插、外推效果，沿模型水平方向，在0～1.5 km 范围内等间距设置21 个控制点，提取煤层的平均速度，如图3a 所示。用四次多项式法和克里金法，分别插值生成相应的平均速度。在内插段，2 种方法生成的平均速度和真实平均速度高度一致。在外推段(1.5～2.0 km)，四次多项式法的值基本沿着真实速度趋势，但离控制点越远差异越大；克里金法的值迅速远离真实速度趋势，离控制点越远差异越大。

图3 控制点直接插值的平均速度和误差分布Fig.3 Average velocity and error distribution for direct interpolation of control points

计算2 种方法的相对误差，如图3b 所示。在内插段，多项式拟合的平均误差为0.21%，克里金插值的平均误差为0.02%，克里金插值的效果明显占优。在外推段，2 种插值方法的效果都不理想，随着远离控制点，误差迅速增大，其中，四次多项式的平均误差为8.56%，克里金法的平均误差为36.76%。

总之，克里金法和四次多项式法的内插效果理想，外推效果较差，无法达到误差小于±1.5%的《煤矿采区三维地震勘探规范》要求。

4 参考叠加速度的插值效果对比

在煤田地震勘探中，除钻孔和见煤点揭露的平均速度外，地震资料处理获得的叠加速也是重要的速度信息。由DIX 公式可计算获得层速度，进而可计算获得平均速度。虽然叠加速度计算的平均速度精度较低，但其趋势和实际平均速度一致[12]。本次，以叠加速度计算的平均速度为参考，利用回归型支持向量机、多项式拟合和克里金等方法进行插值，对比分析各方法的插值精度。

4.1 基于支持向量机的插值

沿煤层提取平滑后速度模型的平均速度，代表由叠加速度计算的平均速度，如图4a 中虚线所示。和真实平均速度相比，平滑模型的平均速度明显偏高，不同位置差异也有所区别，但两者趋势基本一致。

如3 节所示，在1.0～1.5 km 范围内等间距提取21 个控制点平均速度组成训练集，训练支持向量机的预测模型。输入所有点的位置和平滑模型平均速度，计算所有点的平均速度，如图4a 所示。对比计算值和真实值，发现两者不仅在内插段高度一致，在外推段一致性也较高。计算其相对误差，并和直接插值的误差相对比，如图4b 所示。在内插段，3 种方法的误差都较小，差异不明显。在外推段，基于支持向量机的插值误差虽然大于内插段，但远小于直接插值法，平均值为2.8%。

图4 支持向量机法插值的平均速度和误差分布Fig.4 Average velocity and error distribution for RSVM interpolation

4.2 基于速度差的插值

由第3 节可知，克里金法和多项式法直接外推插值的效果不佳。为了参考叠加速度计算的平均速度，在1～1.5 km 范围内等间距提取21 个控制点平均速度，求取控制点平均速度和平滑模型平均速度之差，并分别利用多项式和克里金插值相应的速度差分布。最后，在平滑模型速度中减去速度差，即可获得基于速度差的煤层平均速度，如图5a 所示。对比多项式插值平均速度和真实平均速度，发现两者不仅在内插段高度一致，在外推段一致性也较高。仅在远离控制点的1.9～2.0 km 段，多项式插值结果开始偏离真实值。对于基于速度差的克里金插值，其结果和多项式插值结果类似，如图5a 所示。

图5 基于速度差插值的平均速度和误差分布Fig.5 Average velocity and error distribution for velocity-difference based interpolation

计算基于速度差的多项式和克里金法插值误差，并将其与基于支持向量机的误差相对比，如图5b 所示。在内插段和大部分外推段，基于速度差的多项式法和克里金法的插值误差小；在远离控制点的外推段，基于支持向量机法的插值误差小。在靠近控制点的外推段，基于速度差的多项式法平均误差仅为0.4%，仅略高于内插段，小于±1.5%的行业标准要求。但在远离控制点的外推段，多项式法和克里金法的插值误差迅速增大，最高达15%。究其成因，除平均速度横向变化较快外；距离较远时，控制点控制能力变弱，也是原因之一。

5 应用实例

为了验证上述二维结论是否适用于实际三维采区，以阳泉矿区某采区的15 号煤层为例进行研究。采区共有钻孔和见煤点131 个，其平均速度平面分布如图6a 所示。在采区东部中间，样点密集处为巷道揭露的见煤点，其他样点为钻孔。除少数受局部构造影响的样点，采区平均速度总体单向递减，东南高、西北低。随机选取其中7 个为验证点(“+”图标)，剩余124 个为控制点。对于所有验证点来说，其分布较均匀，代表性较强。平面上，采区中部和各边界处皆有分布；平均速度上，高、中、低齐全。

分别利用基于速度差的克里金法和回归型支持向量机法，训练预测模型，并预测验证点的平均速度，结果如图6b 所示。对于基于速度差的克里金法来说，当选择球状模型进行变异函数建模，变程设定为1.6 km时效果最好[24]。对于支持向量机法来说，当核函数选取为高斯函数时效果最佳[22-23]。

图6 某采区控制点平面分布和平均速度插值效果交会图Fig.6 Plan distribution of control points and cross plot of true and interpolated average velocities

图6b 中，所有验证点都沿交会图对角线分布，平均速度的真实值和预测值基本一致。计算各验证点的相对误差，发现2 种方法的预测精度都较高，平均误差远小于行业标准±1.5%的要求。其中，克里金插值法的最小、最大误差分别为0.06%、1.46%，平均误差为0.44%；回归型支持向量机法的最小、最大误差分别为0.16%、1.50%，平均误差为0.66%。总体来说，基于速度差的克里金法插值精度略高于回归型支持向量机法。

6 结论

a.正演模型计算结果表明，利用克里金法和多项式法直接插值时，插值精度受插值点位置影响巨大。当插值点位于内插段时，插值效果理想；当插值点位于外推段时，插值效果迅速恶化。

b.参考叠加速度的平均速度插值效果明显优于平均速度直接插值，当插值点位于外推段时，这一现象尤为明显。

c.参考叠加速度插值时，在外推段的不同位置，回归型支持向量机法、多项式法和克里金法的插值效果有所不同。在靠近控制点的外推段，基于速度差的克里金法效果最佳；在远离控制点的外推段，基于支持向量机的插值精度最高。

d.本次提出的基于速度差的克里金法和回归型支持向量机法在三维地震实例中应用效果好，平均速度插值误差远小于行业标准要求，适合大范围推广应用。

e.煤炭智能开采需要高精度的煤层底板高程，虽然本次研究取得了明显成效，但距煤炭智能化开采的实际需求还有差距，还需持续深入研究。