顾及降雨影响的动态优化时滞时序GM(1,2)模型在滑坡位移预测中的应用

高雅萍，陈 曦，涂 锐

1. 长安大学地质工程与测绘学院，陕西 西安 710054； 2. 成都理工大学地球科学学院，四川 成都 610059； 3. 中国科学院国家授时中心，陕西 西安 710600

滑坡位移的数值预测有助于滑坡变化机理的研究和滑坡灾害的预警，滑坡的实际形变受到诸多因素的影响，其中降雨对滑坡位移的影响较为明显。基于滑坡监测数据，通过研究环境影响因素的作用原理，分析滑坡位移的变化趋势，建立预测预报模型，对滑坡的防灾减灾具有重要意义[1-4]。

目前，国内外学者对滑坡预测的研究主要集中于滑坡诱发因子和位移变化的作用关系，并以此为滑坡灾害变化机理建立数值预测预报模型，对滑坡位移进行预测研究和分析，主要的预测模型有灰色模型[5]、统计机器学习模型[6]及线性回归模型[7]等。对于受环境影响的滑坡变形预测，通常采用时间序列加法分解滑坡位移，分离出滑坡累计位移中的趋势位移和周期位移并分别预测，最后再叠加复原[8]。目前常用的分解方法有移动平均法[9]、指数平滑法[10]及模态分解法[11]等，本文采用适用于非线性非平稳数据分析处理的经验模态分解法[12]，基于相近模态组合实现时间序列分解。

滑坡体变化系统在实际演化中存在随机性和影响结构模糊性，具有灰色特性，因此可以通过灰色模型来描述滑坡系统内部连续发展变化的数值机理。已经有许多学者应用灰色预测模型或改进模型研究地质形变位移预测[13-15]。文献[16]利用残差修正的GM(1,1)模型对滑坡位移进行预测；文献[17]利用改进的中心逼近式灰色GM(1,1)模型预测滑坡位移；这些灰色模型都没有引入影响因子数据，只是对滑坡位移本身进行趋势预测。文献[18]利用动态多变量灰色模型进行危岩变形预测，可以看到灰色预测模型在滑坡位移预测研究中广泛应用，但这些灰色预测模型的应用还没有将影响因子与滑坡形变变化机理深度融合起来。研究表明滑坡体受环境因素的作用是需要一定时间来完成的[19-21]，一般情况下，滑坡位移不会随着环境因素的变化而立刻变化，存在时间上的滞后性，所以需要对环境变量和滑坡位移时间错位准确评价分析。文献[22]利用动态GM(1,N)模型并考虑时滞影响对受降雨和库水位影响的滑坡速率进行了预测，同时对预测模型本身也需要进行改进以提高预测精度。文献[23]将新陈代谢灰色模型GM(1,1)应用于滑坡位移预测中，提高了位移的预测精度。文献[24]针对传统灰色模型在背景值取值方面存在的缺陷,将基于背景值优化的灰色模型引入滑坡变形预测中。本文在时间序列分解的基础上，应用GM(1,2)模型预测滑坡周期位移。GM(1,2)模型引入了降雨量影响因子对位移变化的预测进行控制，但GM(1,2)模型受到本身数据构造误差的影响预测精度不高。因此，本文提出一种改进的时滞GM(1,2)预测模型。将背景值优化与动态新陈代谢灰色模型结合，将两种改进方法引入考虑时滞影响的GM(1,2)预测模型中，构建基于背景值优化的动态时滞GM(1,2)模型，对受降雨量变化影响的滑坡位移的周期序列进行预测。对于较易预测的趋势序列，建立门限自回归模型进行预测，门限自回归模型是在自回归(AR)模型的基础上增加了门限区间约束条件[25-26]，以自适应分段提高预测精度。

针对受降雨量变化影响的滑坡，对于降雨量变化对滑坡位移数值的滞后影响问题，本文以福宁高速公路八尺门滑坡和秭归县八字门滑坡监测数据为算例，研究利用顾及降雨的动态优化时滞时序GM(1,2)组合预测模型准确预测滑坡位移变化，数据分别来源于国家地球系统科学数据中心(http:∥www.geodata.cn)和国家冰川冻土沙漠科学数据中心(http:∥www.ncdc.ac.cn)。首先，将滑坡位移序列经EMD分解和时序重构为滑坡周期位移序列和趋势位移序列；然后，分析评价在不同时滞时间上的周期位移序列与降雨量的相关程度，确定时滞系数，建立顾及降雨影响的基于背景值优化的动态时滞GM(1,2)预测模型，通过与GM(1,1)模型、未考虑时滞影响的GM(1,2)模型和未优化的时滞GM(1,2)模型对比预测精度评价指标，验证模型的精度，并与预测趋势项的门限自回归模型组合，为滑坡位移预测提供一种顾及影响因子时滞和相关性的可行方法。

1 方 法

1.1 基于EMD位移分解

经验模态分解(empirical mode decomposition,EMD)能将数据序列根据自身变化特征分解为不同模态的序列分量[27-28]。

EMD分解步骤[29]为：① 将原位移变化曲线中所有的极大值点和极小值点通过三次样条曲线分别拟合形成原位移曲线的上包络线和下包络线；② 计算上下包络线均值得到第1个位移分量IMF1，将原位移序列减去该IMF，得到一个新的位移序列；③ 若新位移序列中还存在负的局部极大值和正的局部极小值，说明这还不是一个本征模函数位移序列，需要继续分解。将经过步骤②后的新序列再通过步骤①—步骤③计算，可以得到IMF2、IMF3、IMFn…，以此类推，直至符合条件完成EMD分解。

1.2 基于时间序列的位移分解

滑坡位移的产生是由滑坡体内在因素和外部环境变化因素共同作用的，本文研究的滑坡位移诱发因素主要有两方面，一方面是滑坡体自身重力、岩土性质等引起的滑坡自然位移趋势变化；另一方面是降雨引起的周期性位移变化。因此，本文将滑坡总位移序列分解为趋势位移序列和周期位移序列进行研究

wy(t)=qs(t)+zq(t)

(1)

式中，wy(t)、qs(t)、zq(t)、t分别表示滑坡总位移序列、趋势位移序列、周期位移序列和观测期数。

1.3 基于背景值优化的动态时滞GM(1,2)模型

为了建立正确的GM(1,2)模型，保证模型的预测效果，需要在建模前对滑坡位移序列进行级比验证和数据处理[30-31]。原始序列为x0=(x0(1),x0(2),…,x0(n))，n为位移期数，计算位移序列级比

δ(i)=x0(i-1)/x0(i)i=2,3,…,n

(2)

当所有δ(i)都处于区间(e-2/(n+1),e2/(n+1))内时，数据可用于建立正确的灰色预测模型。如果不符合级比验证，则需要进行数据平移，计算数据平移后的新位移序列再进行级比验证y0(n)=x0(n)+S，S为数据平移常数。

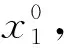
各原始序列为

(3)

(4)

分别一次累加序列为

(5)

(6)

式中

(7)

(8)

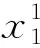
(9)

对两个序列建立时滞GM(1,2)微分方程

(10)

微分方程离散化为

(11)

为解微分方程，构建参数矩阵B、常数向量Y

(12)

(13)

式中，B为系数矩阵；Y为常数向量。

根据最小二乘法求解微分方程系数向量

(14)

代入系数向量和时滞系数后微分方程时间响应式为

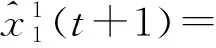
(15)

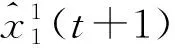
(16)

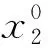
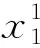
t=2,3,…,n

(17)

式中，w为计算优化背景值的序列紧邻值权重，通过在w∈[0,1]中搜索最优权重，构造最优背景值序列，提高模型预测精度。

(3) 模型动态预测。传统的灰色模型是利用全部样本位移数据拟合建模，模型描述位移整体变化趋势较好，但在反映周期位移变化时，受位移波动性影响较大，预测效果较差。因此，本文为提高时滞GM(1,2)模型的预测效果，建立动态时滞GM(1,2)预测模型，采用对拟合预测数据新陈代谢动态更新的思想[34]，优化时滞GM(1,2)模型的预测效果。

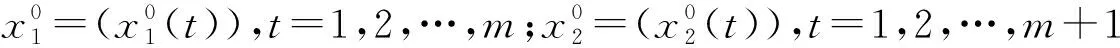
(5) 基于背景值优化的动态时滞GM(1,2)模型：① 选择动态预测的建模样本期数，以不同期数建模对比模型拟合精度，获取最优样本期数。② 以最优样本期数为滑动窗口区间动态建立时滞GM(1,2)模型，即在窗口滑动过程中每滑动更新一次则建立一次时滞GM(1,2)模型，同时在每次建模过程中以均方差最小搜索最优背景值权重，每次建模完成后输入最新降雨数据预测最新位移，实现动态优化时滞GM(1,2)模型。

由此建立了对滑坡周期位移序列进行建模预测的基于背景值优化的动态时滞GM(1,2)预测模型。

1.4 门限自回归模型

本文利用门限自回归(threshold auto regressive,TAR)模型[35-36]对滑坡趋势位移序列进行预测。该模型利用门限分割的方法对数据序列分段建模，能详细描述趋势序列的变化情况。

TAR模型是分段的自回归模型(AR模型)，在观测序列xi的值域范围内设置n-1个门限值ri(i=1,2,…,n-1)，整个序列被分成k个门限区间，可用r0、rn分别表示上界和下界，并设置延迟步数d将xi按xi-d值的大小分配到不同的门限区间内，再对区间内的xi采用不同阶数的AR模型，从而形成序列的分段动态详细描述模型，其模型形式为

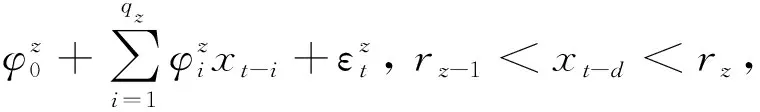
z=1,2,…,n

(18)

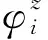
(19)

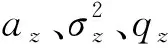
本文所建立的组合预测方法流程如图1所示。

图1 预测方法流程Fig.1 Forecast method flowchart

2 试验分析

本文以福宁八尺门滑坡和秭归县八字门滑坡为研究对象，共两例模型验证试验分析。

试验例1以福宁八尺门滑坡作为研究对象，福宁八尺门滑坡位于福建省宁德市福鼎白岩村，海拔0～290 m。地层分布为上覆坡积碎石土及残积亚黏土，含水层降水补给来源为大气降雨垂直渗透，下伏石帽山群下段下组英安质晶屑凝灰岩,局部为凝灰岩。选择3ZK08监测点48期监测数据，时间为2001年7月15日—2003年6月29日，滑坡位移采样间隔为15 d，作为以15 d为一个观测期的等时间间隔序列进行数据处理，降雨序列为每15 d为周期的总降雨值。试验例2以三峡库区秭归县八字门滑坡GPS地表位移监测数据为例，八字门滑坡位于三峡库区湖北省秭归县归州镇的长江北岸支流香溪河右岸河口处，下距三峡大坝31 km。滑坡体位于香溪河右岸，岸坡呈南北走向，滑坡体呈撮箕状展布于岸坡坡脚，根据数据完整性和有效性选择滑坡体中上部监测点ZG111的2007年1月—2012年4月监测数据进行数据处理和分析，滑坡位移采样间隔为1个月，作为以1个月为一个观测期的等时间间隔序列进行数据处理，降雨序列为每1月为周期的总降雨值。

以两例滑坡位移监测点数据和滑坡区降雨量采集数据为基础，研究降雨量变化对滑坡体周期位移序列的影响并建立顾及降雨的动态优化时滞时序GM(1,2)组合滑坡位移预测模型对滑坡实例数据进行预测和精度验证分析。

2.1 试验1

2.1.1 基于EMD分解及位移时序重构

首先利用EMD方法将滑坡位移序列分解为不同模态分量，对比不同EMD迭代次数可知，迭代次数设置为50～90时分解得到的趋势序列符合滑坡累计位移的自然变化，时序重构得到的周期序列能较好反映滑坡累计位移的波动情况，本文试验迭代次数设置为70进行分解，如图2所示，滑坡位移序列分解后有4个不同频率分量。根据时间序列位移分解方法，其中IMF4位移序列分量为单调递增趋势，所以将IMF4位移序列分量作为滑坡的趋势位移序列。IMF1—IMF3为变化频率各不相同的3个位移序列分量，将3个分量叠加得到滑坡的周期位移序列。重构后的时间序列位移如图3所示。

图2 EMD分解结果Fig.2 EMD decomposition results

图3 时间序列方法位移重构结果Fig.3 Displacement reconstruction results of time series method

2.1.2 周期位移序列与降雨量相关性分析

在滑坡受自身重力滑动过程中，降雨从滑坡体地表向下渗透，对滑坡位移会有一定的加速作用，降雨会使滑坡体含水量增加，使土体孔隙压力增大而滑坡体抗滑阻力降低，含水量的增加也会使滑坡体重量增加而增大滑坡下滑力。另外，本文研究对象福宁八尺门滑坡地质存在黏土层，由于黏土有机质含量多土壤胀缩性较大，降雨会使土壤吸水膨胀，降雨减少使土壤脱水干燥，这也会影响滑坡监测位移的周期性变化。同时降雨对滑坡位移的影响并不是实时作用，在降雨从滑坡体地表向下渗透到影响位移变化过程中会有一个时间滞后。本文综合考虑降雨对滑坡的周期位移序列的时滞作用和位移值变化影响。

基于EMD分解和时间序列的分解结果研究降雨量与周期位移序列的相关性和时滞性。滑坡区降雨量与滑坡监测点周期位移序列关系如图4所示。

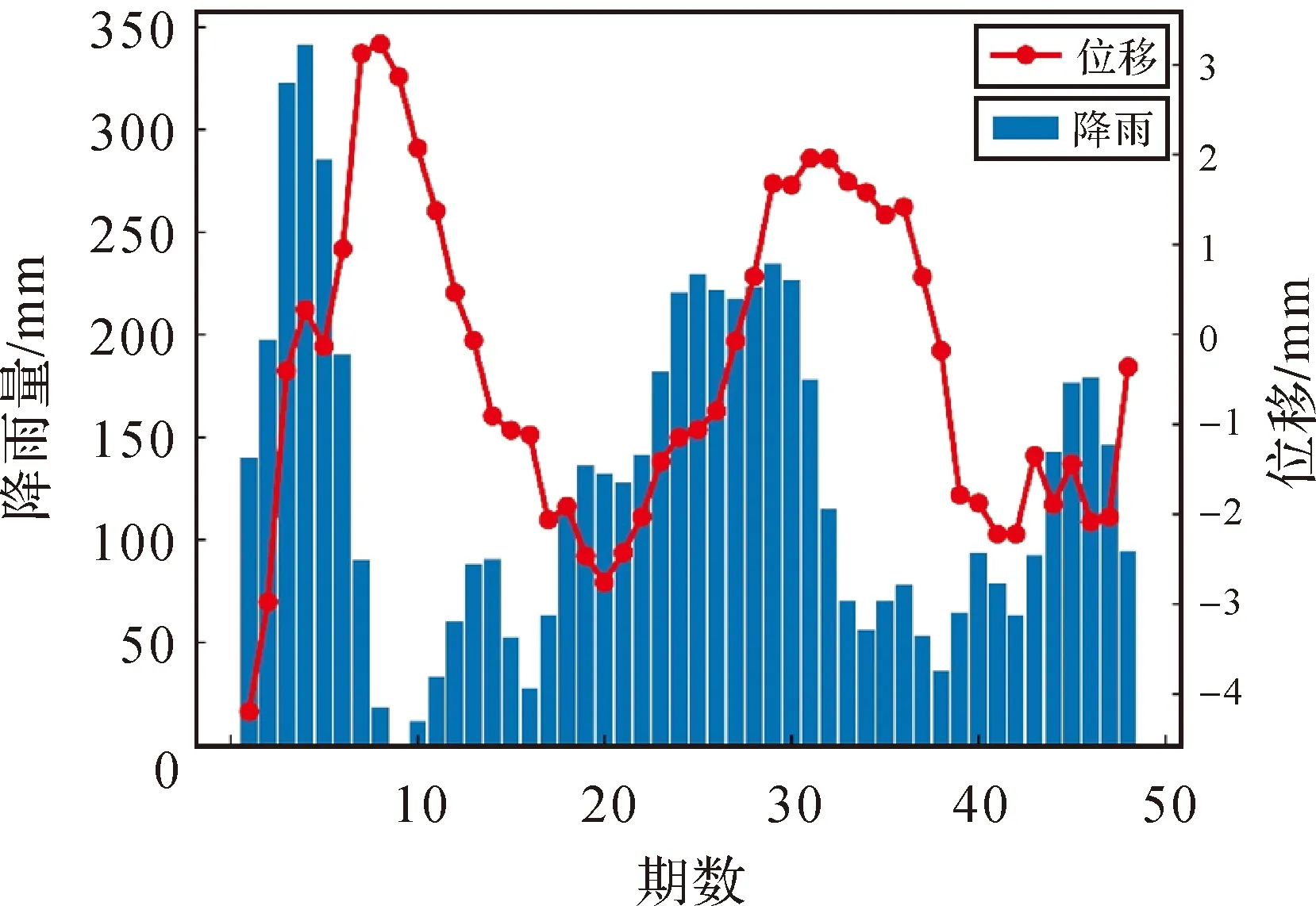
图4 降雨-滑坡周期位移序列关系Fig.4 Periodic displacement sequence diagram of rainfall and landslide

根据图4分析整体降雨量和位移变化趋势，随着降雨量的波动变化，滑坡的周期位移序列也存在一个波动变化，并且两者变化值的波形规律近似一致，但是周期位移序列数值变化相对于降雨量数值变化存在时间上的滞后性。

对降雨量变化序列和滑坡周期位移变化序列进行相关性分析，降雨量序列和滑坡周期位移序列都是以观测期为单位的等时间间隔序列，利用Pearson相关系数模型(式(20))，设置不同时滞时间，即位移序列相对于降雨序列同期数据的滞后期数，将位移序列首部的滞后期数数据和降雨序列尾部的滞后期数数据分割构建时滞降雨-位移变化序列组，通过比较不同时滞降雨-位移变化序列组的相关性程度，确定时滞GM(1,2)模型的时滞时间系数d，即分析周期位移变化相对于降雨的滞后程度。

Pearson相关系数r计算式为[37]

(20)

从0～9个时滞观测期依次进行时滞相关性分析，其结果如图5所示，其中相关性最大的是时滞为第5个观测期，d=5时，P≤0.01、r=0.82，属于高度相关，即滞后5个观测期后，降雨量与周期位移序列相关性最大，此时降雨量变化和周期位移序列变化最相关。

图5 降雨-滑坡周期位移序列时滞Pearson相关分析Fig.5 Time delay Pearson correlation analysis diagram of rainfall-landslide periodic displacement series

2.1.3 基于背景值优化的动态时滞时序GM(1,2)组合模型预测分析

本文建立顾及降雨影响的背景值优化动态时滞GM(1,2)预测模型，预测周期位移序列是将预测期数的降雨量数据输入所建立的动态优化时滞GM(1,2)模型，由模型计算得到降雨量滞后影响下的周期位移值。数据序列为以观测期为单位的等间隔采样值，经过相关性分析得到的时滞时间为5个观测期(d=5)，因此选取第1～33期降雨量序列和第6～38期周期位移序列作为样本数据集进行模型拟合建模，将位移序列进行级比验证，将降雨量数据序列进行平滑，两者建立模型计算位移预测时间响应式参数，将第34～43期降雨量数据输入建立的动态预测模型，预测第39～48期周期位移序列数据。优化背景值权重区间为[0,1]，在动态预测过程中不断更新权重，将最优背景值权重引入动态建模过程进行预测。经试验测试，动态预测样本区间大小选择为10～33，对拟合预测结果平均绝对误差、均方差、平均相对误差定权，综合比较确定精度最高的样本区间，选择动态建模样本区间为12期。

为分析验证顾及时滞因素预测模型的动态预测精度和优化效果，确定引入影响因子和时滞条件下动态优化时滞GM(1,2)预测模型的有效性。本文同时建立了GM(1,2)滑坡位移预测模型、GM(1,1)滑坡位移预测模型和时滞GM(1,2)滑坡位移预测模型，对比分析模型对周期位移序列的预测效果，如图6所示。

图6 各模型预测结果曲线Fig.6 Prediction result curve of each model

图6中，结合原始值可知动态优化时滞GM(1,2)模型预测的效果相比传统模型大幅提高；GM(1,2)模型预测效果较差，主要是因为未顾及降雨的时滞影响导致降雨影响因子成为预测误差源，使GM(1,2)模型预测误差较大；GM(1,1)模型存在指数性预测趋势，对于周期位移序列的波动性预测效果较差。

为准确评价动态优化时滞GM(1,2)模型的预测精度，本文选取均方根误差(RMSE)、平均相对误差(MRE)作为评价指标，通过与GM(1,1)、GM(1,2)模型和时滞GM(1,2)模型进行比较，验证动态优化时滞GM(1,2)模型的预测效果

(21)

(22)

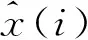
动态优化时滞GM(1,2)模型预测精度最高，预测均方根误差为0.542 7 mm/期(表1)。在预测均方根误差方面，动态优化时滞GM(1,2)模型比时滞GM(1,2)模型提高了21.7%，比GM(1,1)模型提高了74.7%，比GM(1,2)模型提高了79.8%；在预测平均相对误差方面，动态时滞GM(1,2)模型比时滞GM(1,2)模型提高了35.1%，比GM(1,1)模型提高了81.1%，比GM(1,2)模型提高了81.3%。动态优化时滞GM(1,2)模型对于滑坡位移周期项的预测精度完全优于传统模型，并且经过优化，预测精度较未优化时滞GM(1,2)模型更高。结合图6和表1，发现GM(1,2)模型比GM(1,1)模型预测精度更低，说明了考虑影响因子与变量之间时滞影响的重要性。

表1 模型精度评价

在建立动态优化时滞GM(1,2)预测模型的同时，对滑坡趋势位移序列进行建模预测。本文以门限自回归模型对趋势位移序列建模拟合预测，为与周期位移序列预测结果组合，选取第6～38期趋势位移序列作为建模数据，建立门限自回归预测模型，门限区间个数取2，最大门限延迟量设置为5，自回归最大阶数为5，默认最小AIC值为1×1010，在样本的30%～70%分位区间以1%进度搜索最优门限值。预测步长为一步，预测后数据更新，再进行下一步预测，实现模型的动态更新和预测。经过动态预测得到第39～48期预测趋势位移序列数据，预测结果值见表2，预测残差逐渐增大，其预测误差随预测期数增加逐渐变大，预测平均绝对误差为0.004 mm，拟合优度达到0.999 9，预测精度高，能有效预测滑坡趋势位移序列变化情况。

表2 趋势序列预测结果

将滑坡周期位移预测序列和趋势位移预测序列叠加，实现最终滑坡真实位移序列的预测，本文建立了顾及降雨影响的动态优化时滞时序GM(1,2)组合滑坡位移预测模型，同时建立EMD-LSTM-TAR、EMD-BPNN-TAR组合模型与本文方法进行对比，对比模型的建立方法同样采用时序分解预测再组合的方法，LSTM和BPNN模型分别作为各自组合模型的周期序列预测方法，各模型预测结果曲线如图7所示。由图7可知，本文方法预测效果较好，预测结果更符合观测值变化情况，预测结果均方差为0.288 1 mm2，拟合优度可达0.906 0。

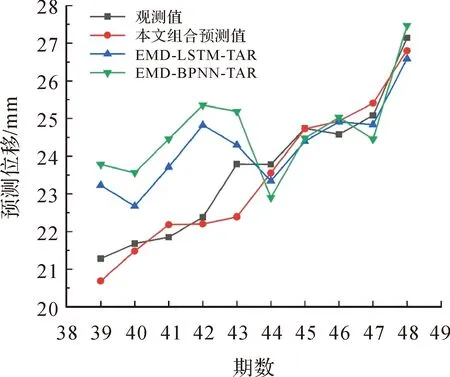
图7 滑坡位移预测结果Fig.7 Prediction result of landslide displacement

2.2 试验2

2.2.1 基于EMD分解及位移时序重构

首先利用EMD方法将滑坡位移序列分解为不同模态分量，迭代次数设置为70时分解得到的趋势序列符合滑坡累计位移的自然变化，分解后分量如图8所示，其中IMF4位移序列分量为单调递增趋势，所以将IMF4作为滑坡的趋势位移序列。IMF1—IMF3为变化频率各不相同，因此叠加得到滑坡的周期位移序列。重构后的时间序列位移如图9所示。

图8 EMD分解结果Fig.8 EMD decomposition results

图9 时间序列方法位移重构结果Fig.9 Displacement reconstruction results of time series method

2.2.2 周期位移序列与降雨量相关性分析

基于EMD分解和时间序列的分解结果研究降雨量与周期位移序列的相关性和时滞性。滑坡区降雨量与滑坡监测点周期位移序列关系如图10所示。由图10可知，周期位移变化相对于降雨量变化存在一定的滞后。

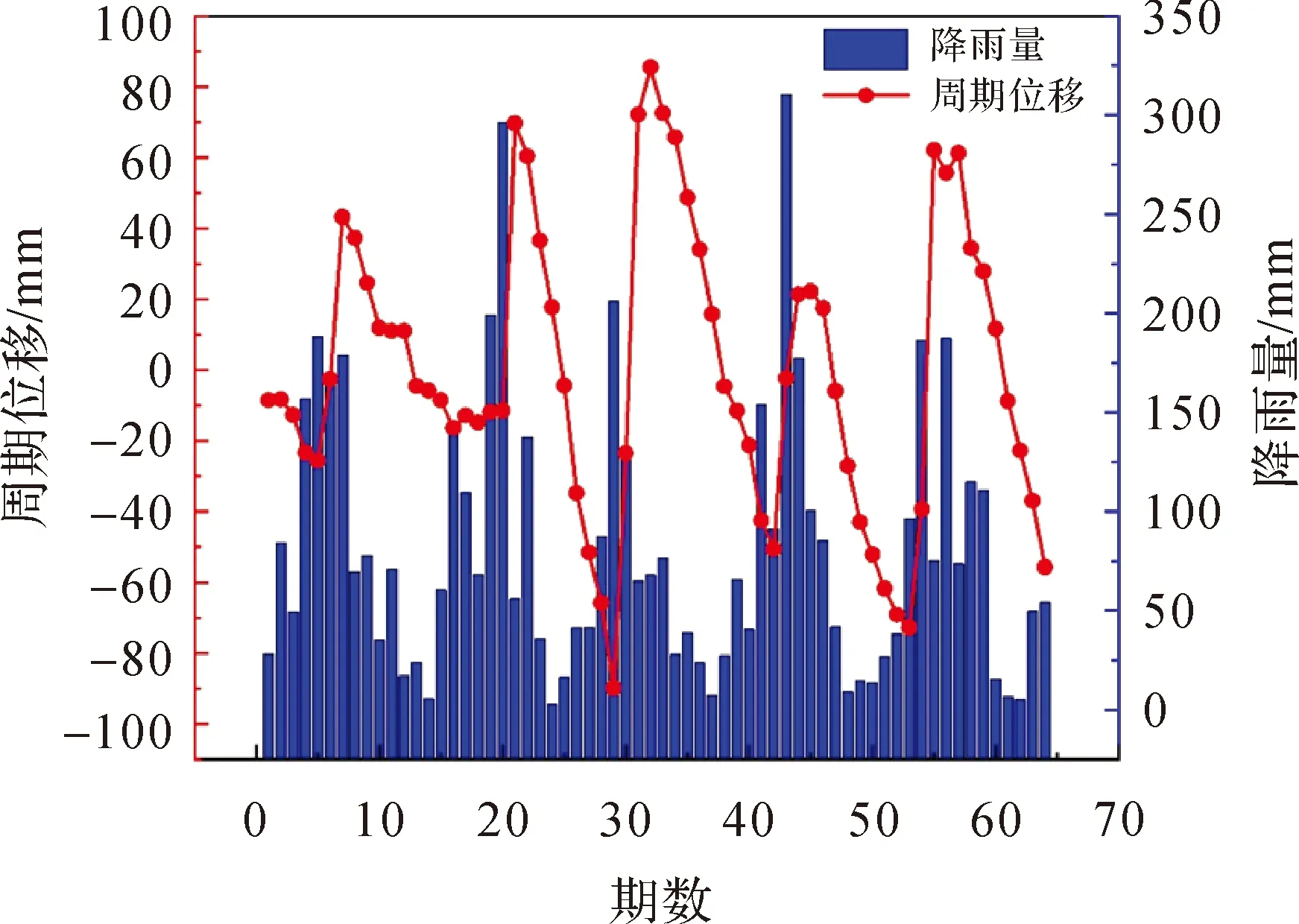
图10 降雨-滑坡周期位移序列关系Fig.10 Periodic displacement sequence diagram of rainfall and landslide

对降雨量变化序列和滑坡周期位移序列变化序列进行相关性分析，利用Pearson相关系数模型，设置不同时滞时间，比较不同时滞降雨-位移变化序列组的相关性程度，从0～5个时滞观测期依次进行时滞相关性分析，其结果如图11所示，其中相关性最大的是时滞为第2个观测期，d=2时，P≤0.01、r=0.59，属于中等程度相关，即滞后2个观测期后，降雨量与周期位移序列相关性最大，因此本实例时滞系数为2期。

图11 降雨-滑坡周期位移序列时滞Pearson相关分析Fig.11 Time delay Pearson correlation analysis diagram of rainfall-landslide periodic displacement series

2.2.3 基于背景值优化的动态时滞时序GM(1,2)组合模型预测分析

建立顾及降雨影响的背景值优化动态时滞GM(1,2)预测模型，预测周期位移序列，经过相关性分析得到的时滞时间为2个观测期(d=2)，因此选取第1～38期降雨量序列和第3～40期周期位移序列作为样本数据集进行模型拟合建模，将位移序列进行级比验证，将降雨量数据序列进行平滑，将第39～62期降雨量数据输入建立的动态预测模型，预测第41～64期周期位移序列数据。优化背景值权重区间为[0,1]，在动态预测过程中不断更新权重，将最优背景值权重引入动态建模过程进行预测。经试验测试，动态预测样本区间大小选择为10～38，对拟合预测结果平均绝对误差、均方差、平均相对误差定权，综合比较确定精度最高的样本区间，选择动态建模样本区间为30期。本文同时建立了GM(1,2)滑坡位移预测模型、GM(1,1)滑坡位移预测模型和时滞GM(1,2)滑坡位移预测模型，对比分析模型对周期位移序列的预测效果，如图12所示，各模型的预测精度评价指标见表3所示。

表3 模型精度评价

图12 各模型预测结果曲线Fig.12 Prediction result curve of each model

由图12结合表3可知，动态优化时滞GM(1,2)模型预测的精度相比传统模型大幅提高，与时滞GM(1,2)模型对比，模型改进的优化效果得到体现；GM(1,2)模型存在超前预测，主要是因为真实位移与因降雨预测得到的位移相比有一定滞后，使GM(1,2)模型预测出现误差；GM(1,1)模型存在指数性预测趋势，对于周期位移序列的波动性预测效果较差。

建立门限自回归模型对趋势位移序列建模拟合预测，为与周期位移序列预测结果组合，选取第3～40期趋势位移序列作为建模数据，建立门限自回归预测模型，门限区间个数取2，最大门限延迟量设置为5，自回归最大阶数为5，默认最小AIC值为1×1010，在样本的20%～70%分位区间以3%进度搜索最优门限值。经过动态预测得到第41～64期预测趋势位移序列数据，预测结果值见表4，预测残差逐渐增大，其预测误差随预测期数增加逐渐变大，预测平均绝对误差为0.168 5 mm，拟合优度达到0.999 9，能有效预测滑坡趋势位移序列变化情况。

表4 趋势序列预测结果

将滑坡周期位移预测序列和趋势位移预测序列叠加，实现最终滑坡真实位移序列的预测，本文建立了顾及降雨影响的动态优化时滞时序GM(1,2)组合滑坡位移预测模型，同时建立EMD-LSTM-TAR、EMD-BPNN-TAR组合模型与本文方法对比，对比模型的建立方法同样采用时序分解预测再组合的方法，LSTM和BPNN模型分别作为各自组合模型的周期序列预测方法，各模型预测结果曲线如图13所示。由图13对比各模型滑坡位移预测结果，本文方法预测效果最好，预测结果均方差为27.535 9 mm2，拟合优度可达0.960 1。

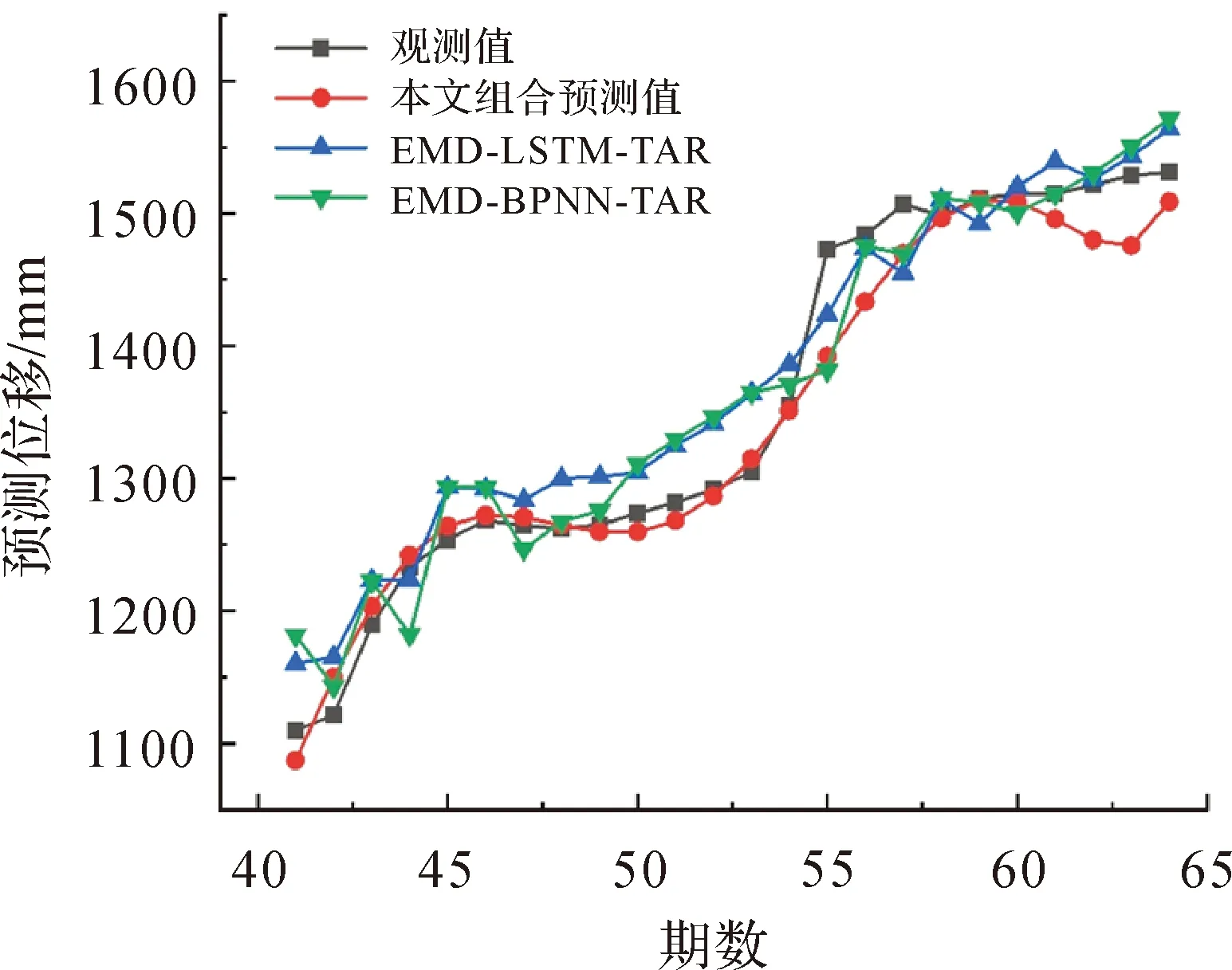
图13 滑坡位移预测结果Fig.13 Prediction results of landslide displacement

3 结 论

针对降雨对滑坡位移的影响问题，结合福宁八尺门滑坡和秭归县八字门滑坡监测数据，利用EMD和时序位移重构的方法将滑坡位移序列分解为趋势位移序列和周期位移序列，分析了降雨量变化对滑坡周期位移序列的时滞相关作用，建立了结合背景值优化的动态时滞GM(1,2)预测模型，将降雨量序列输入模型得到周期预测位移，同时建立了门限自回归模型预测趋势位移。经对比预测结果，表明动态优化时滞GM(1,2)预测模型在降雨因子影响下的预测效果明显优于GM(1,2)、GM(1,1)和时滞GM(1,2)模型。基于降雨量数据预测滑坡周期位移序列，通过灰色系统来描述滑坡位移的波动变化，反映了时期降雨量在观测期间对滑坡体的作用。基于本文建立的顾及降雨影响的动态优化时滞时序GM(1,2)组合滑坡位移预测模型，以滑坡监测实例位移数据为例，分别对周期位移序列和趋势位移序列进行预测，最后叠加得到的预测结果，通过与建立的EMD-LSTM-TAR、EMD-BPNN-TAR组合模型对比得到本文预测方法精度较高，这些高精度的位移预测结果对滑坡灾害的监测预测预警具有一定的应用价值。

随着滑坡监测技术的发展，将能获取更高采样率和更多变量因子的监测数据，在对滑坡变化的整体数值分析中，融入时滞影响对滑坡位移的变化将能够提前预知，同时建立学习能力更强的数值预测模型，提高影响因子数据集映射到位移变化的精度，实现更准确的滑坡位移变化预测预报，这对滑坡灾害的监测预测预警具有重要意义。