大跨度钢管翼缘组合梁桥车桥耦合振动性能分析

王秀丽， 朱武军， 张雨

(兰州理工大学土木工程学院， 兰州 730050)

相较于传统的钢-混组合梁，管翼缘组合梁是用内填混凝土的钢管代替工字钢上翼缘的一种新型组合结构梁。钢管的高度降低组合梁腹板的高度，避免了组合梁腹板长细比过大的问题，内部混凝土由于方钢管的套箍作用，从而提高其承载力，并且防止了钢管因受压而发生的局部屈曲破坏。在荷载的作用下，钢管混凝土受压，钢梁下部受拉，充分发挥混凝土和钢材的材料性能，在施工过程中采用钢管作为混凝土浇筑模板，既节约了成本又方便了施工[1]。

目前，中外学者已对管翼缘组合桥梁的屈曲性能、疲劳性能、抗扭性能及抗弯性能等力学性能进行了研究，并取得了一定的研究成果[2-5]。Wang等[6]通过对比了平腹板与波纹腹板的钢管翼缘组合梁在集中静力荷载下的作用，得到了其弯曲极限承载力和力学行为，并总结了钢管翼缘组合梁的弯曲破坏机理。陈克珊[7]对单、双轴对称的钢管混凝土翼缘工字形组合梁的扭转与弯扭屈曲问题进行理论研究。付烨[8]对3种不同截面类型的矩形上翼缘钢管混凝土组合梁进行了抗弯试验研究，推导出3种组合梁截面的弹塑性抗弯承载力。以上大多以管翼缘组合梁静力分析为主，但对其动力性能研究较少，尤其在车桥耦合方面。

早期的车桥耦合振动研究主要是以现场测试为主，直到20世纪90年代，一些学者提出具有代表性的车桥耦合模型后，才开始研究比较符合实际情况的车桥耦合作用。郁乐乐[9]以某座简支钢-混组合梁桥为算例，利用已开发的车桥耦合振动响应分析程序，分析了不同的车速、车辆载重、桥面不平整度等级和剪力键刚度对车桥耦合动力响应的影响。Wang[10]分析了车辆装载条件、车速和路面条件等参数因素对桥梁的动力冲击系数、可感知振动水平和乘坐舒适性等指标的影响。魏志刚等[11]建立了以待定系数表达的振动方程，计算了钢-混凝土简支梁的动力特性。桂水荣等[12]利用梁壳组合法和铰接板梁法分别建立三维车桥耦合振动模型分析了空心板桥在不同车速，不同车道以及不同路面平整度下动力性能。安里鹏等[13]利用弹性系统总势能不变值原理和对号入座法则建立了磁浮列车-桥梁耦合系统动力响应方程，分析了行车速度、列车载重、车道数及轨道不平顺等参数对车桥耦合系统的响应。虽然众多学者已经做了不少关于车桥耦合振动的理论研究、数值模拟和实验分析，但很多研究是比较简单和理想化，不能同时考虑车辆惯性、平整度等重要因素，或者计算方法存在缺陷，这些问题会影响桥梁设计的安全性、经济性以及实用性。

针对上述提到的问题，以实际工程为依托，通过有限元软件ABAQUS建立车辆模型和桥梁模型对大跨度管翼缘组合梁桥的车桥耦合振动进行参数响应分析，采用控制变量法，分别考虑车辆的载重、车辆的速度、桥梁管翼缘的含钢率、管翼缘内部混凝土强度等级、桥梁路面不平整度等5类参数对管翼缘组合桥梁动力特性的影响。并与抗弯刚度相同的等效工字钢梁和等效混凝土梁的动力性能进行对比分析，以期为此种类型的桥梁研究和推广提供技术参考。

1 工程结构概况

依托的工程位于兰州市G109线跨连霍高速处的一段高架桥，主桥由三跨管翼缘组合梁(51 m+61 m+51 m)组成，下部结构采用的是钢箱门式框架，柱墩盖梁的跨径为30 m，过渡墩盖梁的跨径为30 m，由于施工现场条件限制，主梁和盖梁采用的斜交方式，其交角为63°，组合梁的管翼缘内填C40自密实混凝土，桥梁断面和组合梁截面形式如图1、图2 所示。

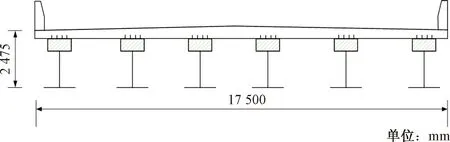
图1 钢混组合桥的断面图Fig.1 Sectional view of steel-concrete composite bridge

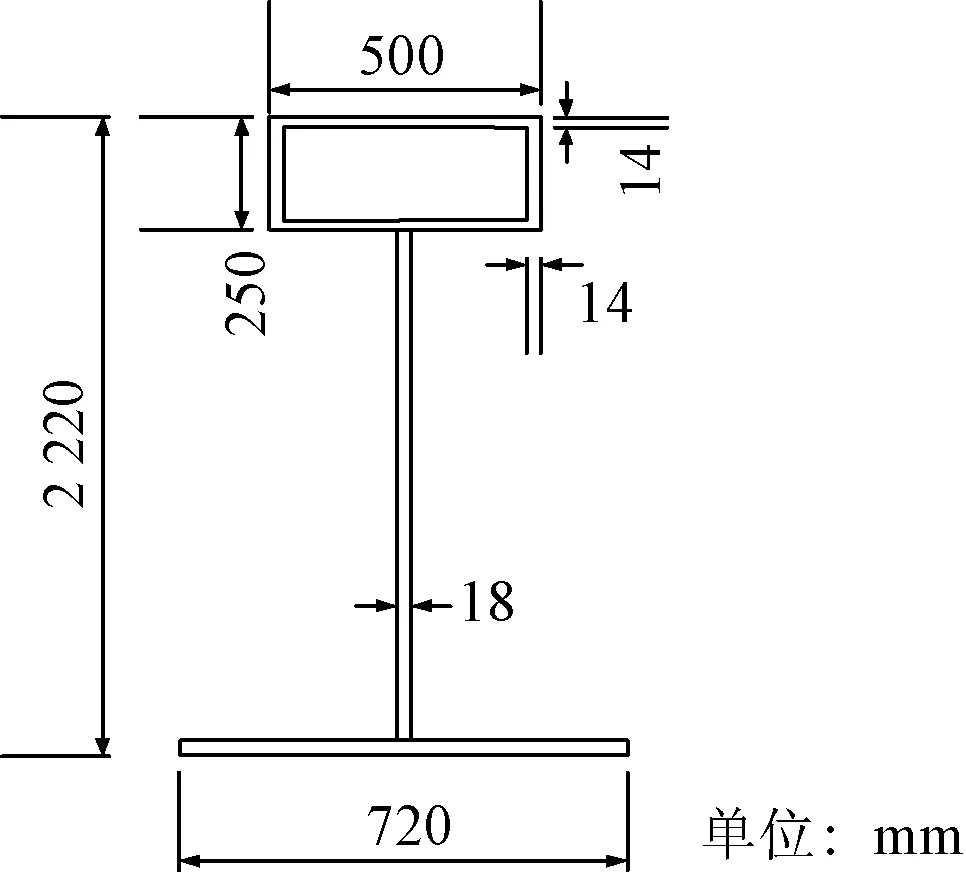
图2 管翼缘组合梁断面图Fig.2 Sectional view of steel-concrete composite beams with upper flange of concrete filled steel tube

2 桥梁和车辆计算模型

2.1 标准车辆模型的建立

车辆的类型、重量、轴距、速度对桥梁结构会产生不同的影响，选用文献[14-15]中常见的三轴车，车辆参数如表1所示，其简化模型如图3所示。

2.2 桥面平整度模拟

桥面平整度作为重要的激励源，在车桥耦合分析中不可忽略。常采用三角级数生成满足功率谱密度函数的路面不平整度曲线来描述。采用《机械振动道路路面谱测量数据报告》(GB/T 7031—2005)[16]中的路面功率谱函数，其表达式为

表1 车辆特征参数

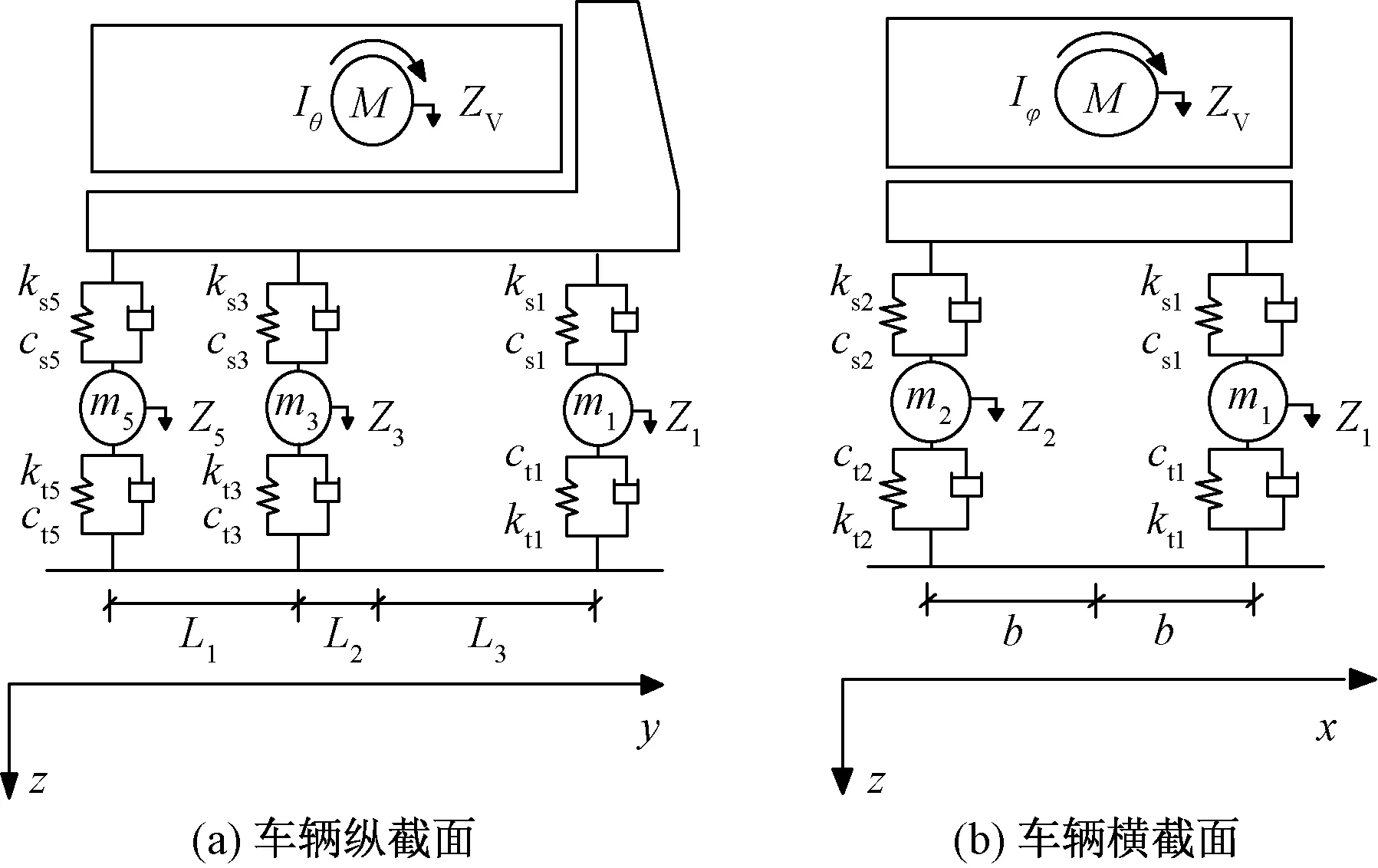
图3 车辆模型简化图Fig.3 Simplified vehicle diagram

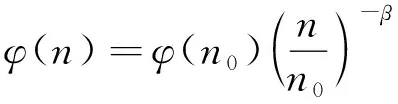
(1)

式(1)中：n为空间频率，m-1；n0为参考空间频率，通常取n0=0.1 m-1；β为频率指数，一般情况下取β=2；φ(n0)为路面不平整度系数，10-6m2/m-1，其值如表2所示；φ(n)为位移功率谱密度，10-6m2/m-1。

在给定路面不平度功率谱后，利用三角级数叠加法模拟路面不平顺样本，其表达式为

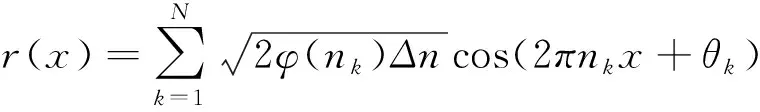
(2)

式(2)中：x为沿着桥纵向的坐标；nk、Δn、N分别为空间频率采集点、采样间距及采样数；θk为在区间(0,2π)上的随机相位角。

利用路面不平顺样本的三角级数叠加法在MATLAB软件中分别模拟出了A级、B级、C级、D级路面[17]曲线，如图 4所示。

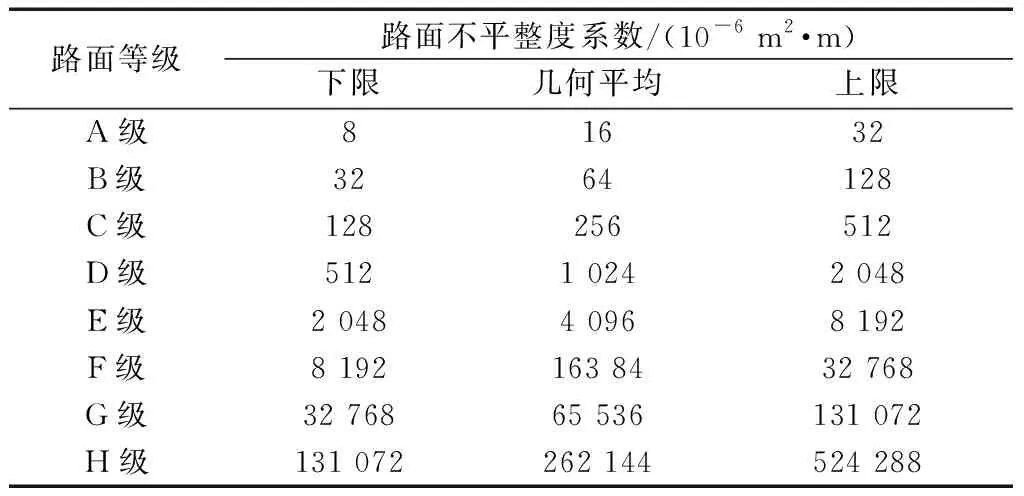
表2 路面不平整度系数

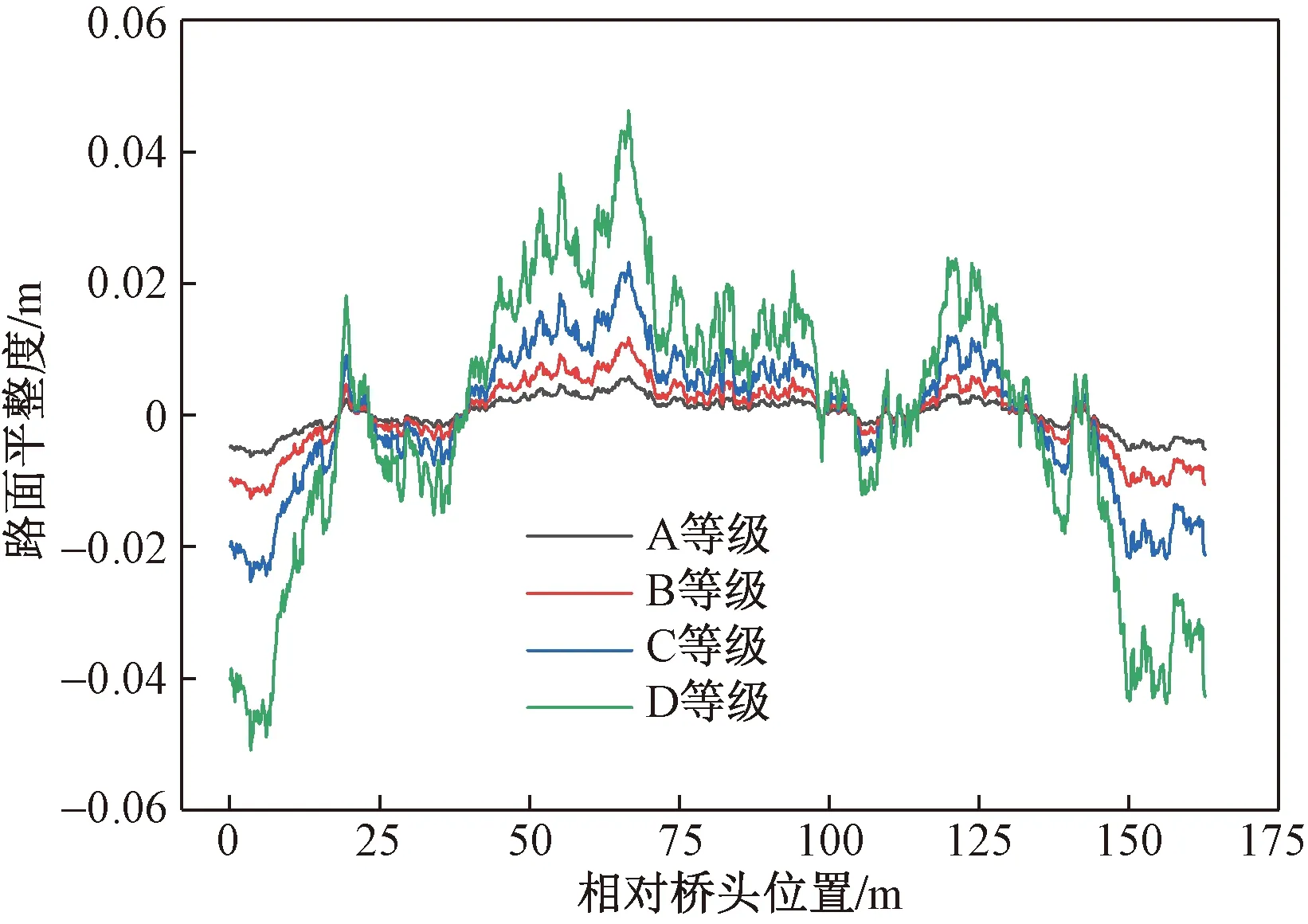
图4 路面平整度曲线Fig.4 Road smoothness curve

2.3 等效截面

桥梁不管在承受动力荷载还是静力荷载作，主梁主要承受弯矩作用。为了与管翼缘组合梁有一定的对比性，根据材料力学的基本原理[18]和《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[19]、《公路桥涵钢结构及木结构设计规范》(JTJ 025—1986)[20]，利用等效截面法分别设计了与管翼缘组合梁的抗弯刚度EI(E为弹性模量，I为截面竖向惯性矩)相同的混凝土截面梁和工字钢截面梁，具体的截面参数如表3所示，其截面如图5所示。

3 车桥耦合方程及求解方法

在建立车桥耦合前方程前，车辆与桥梁的振动方程可表示为矩阵形式[21]，即

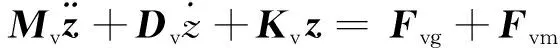
(3)

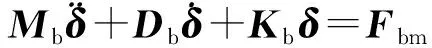
(4)

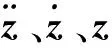
将车辆和桥梁视作两个分离振动体系，二者之间的耦合作用通过车辆轮胎与桥面间的相互作用联系起来，因此桥梁路面和车辆车轮之间的位移存在的关系可表示为

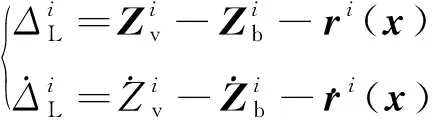
(5)

图6 全桥动力响应控制截面Fig.6 Full bridge dynamic response control section

表3 3种不同类型梁的截面参数

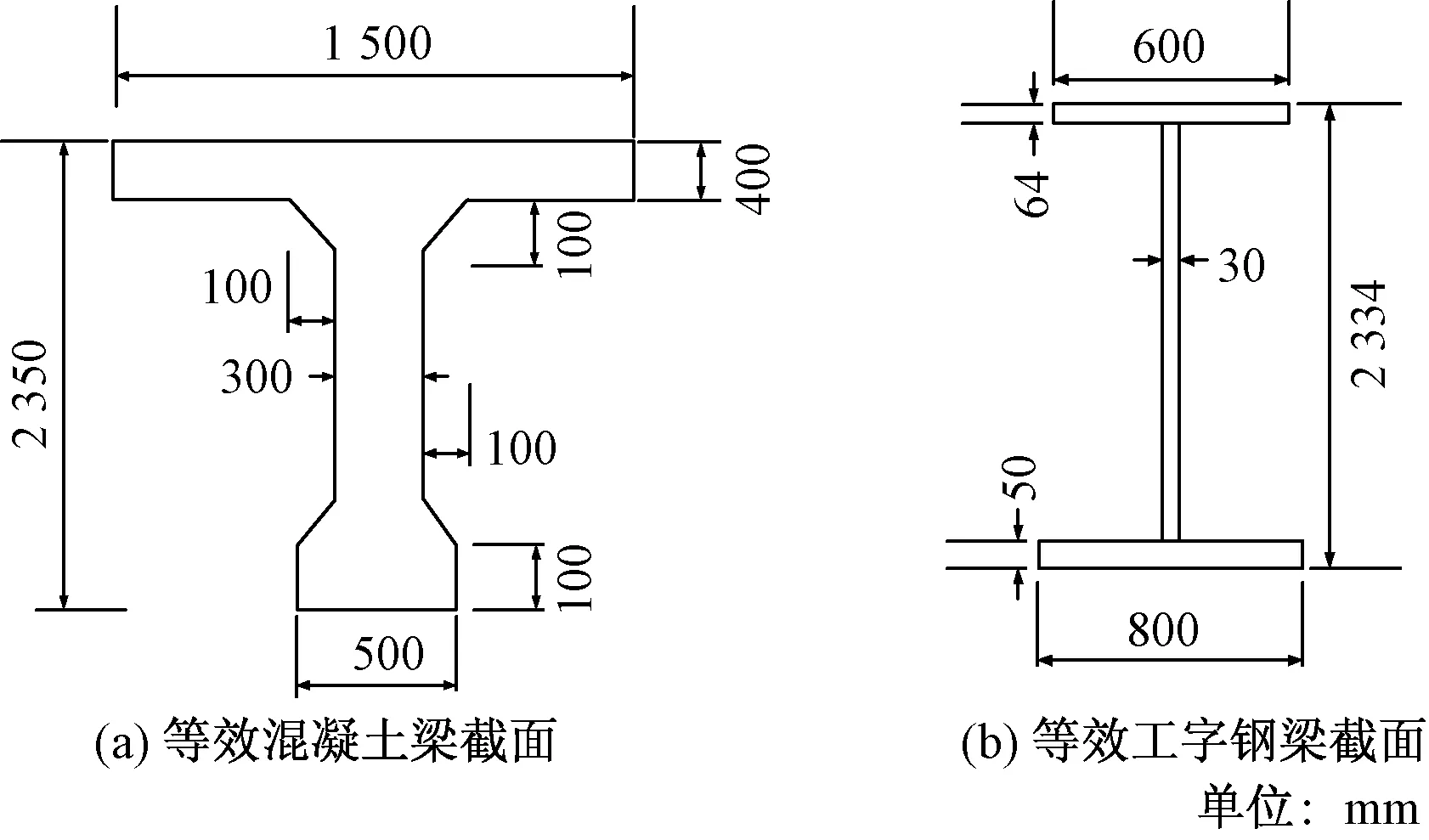
图5 混凝土和工字钢梁截面示意图Fig.5 Schematic diagram of cross-section of concrete beam and 工-steel beam

面平整度，于是桥梁与车轮接触力为

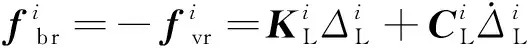
(6)

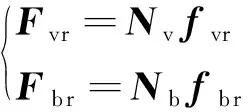
(7)

式(7)中：Nv和Nb分别为车辆和桥梁的形函数；fvr和fbr分别为车辆和桥梁体系间的接触力向量。

将式(5)～式(7)代入式(3)、式(4)可得移动车辆与管翼缘组合桥梁的耦合动力学方程，即

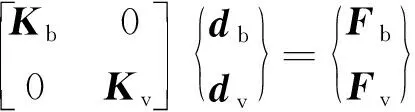
(8)

考虑弹簧、阻尼等对桥梁结构动力响应的影响，采用ABAQUS/Standard动力隐式算法对式(8)进行求解，积分方法为Hilber-Hughes-and Taylor算法，其中α=0.414 214，β=0.5，γ=0.914 214[22]。α为有限元软件ABAQUS隐式动力学中采用的Hilber-Hughes-and Taylor时间积分方法中的权重因子，一般在工程计算中α=-0.414 214，使得计算结果稳定、精确度高，β=(1-α)2×4-1，γ=0.5-α。

选择图6所示的1-1截面中的A点和2-2截面中B点进行了研究，其截面分别如图7、图8所示。

4 有限元模拟

4.1 桥梁模型的模拟

采用ABAQUS软件，建立空间有限元模型，上翼缘混凝土采用C3D8R实体单元，钢板采用S4R壳单元。钢管和混凝土接触采用通用接触，接触属性定义为：接触面法线方向定义为硬接触，切线方向为摩尔-库伦模型，接触面相对滑移，钢管与混凝土的摩擦系数为0.6。桥梁模型如图9所示。

4.2 车辆模型的模拟

车辆模型采用线刚体单元，参考结点采用弹簧阻尼连接，通过在参考结点处施加集中质量，从而将车辆简化为由集中质量、弹簧和阻尼系统组成的三维体系，其模型示意如图10所示。

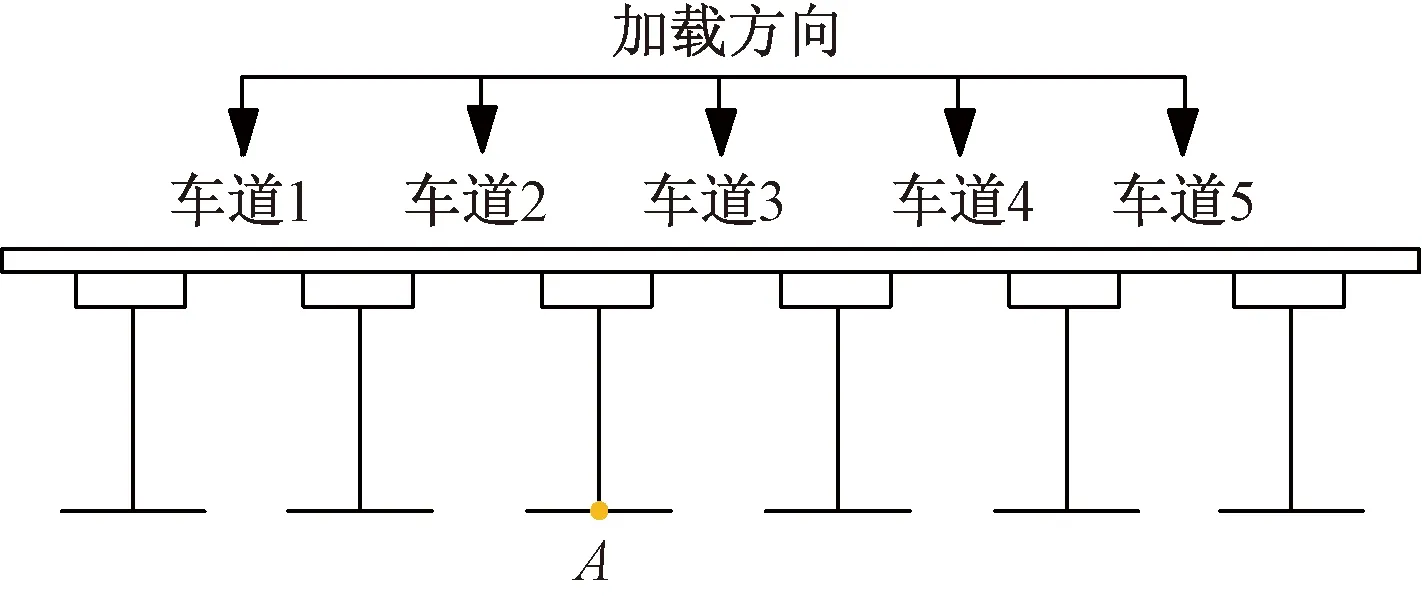
图7 截面1-1控制点Fig.7 Section 1-1 control points

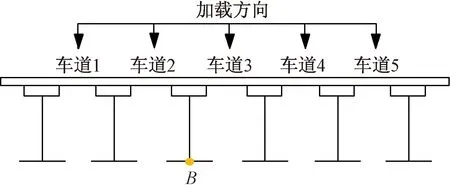
图8 截面2-2控制点Fig.8 Section 2-2 control points

图9 桥梁的有限元模型Fig.9 Finite element model of the bridge

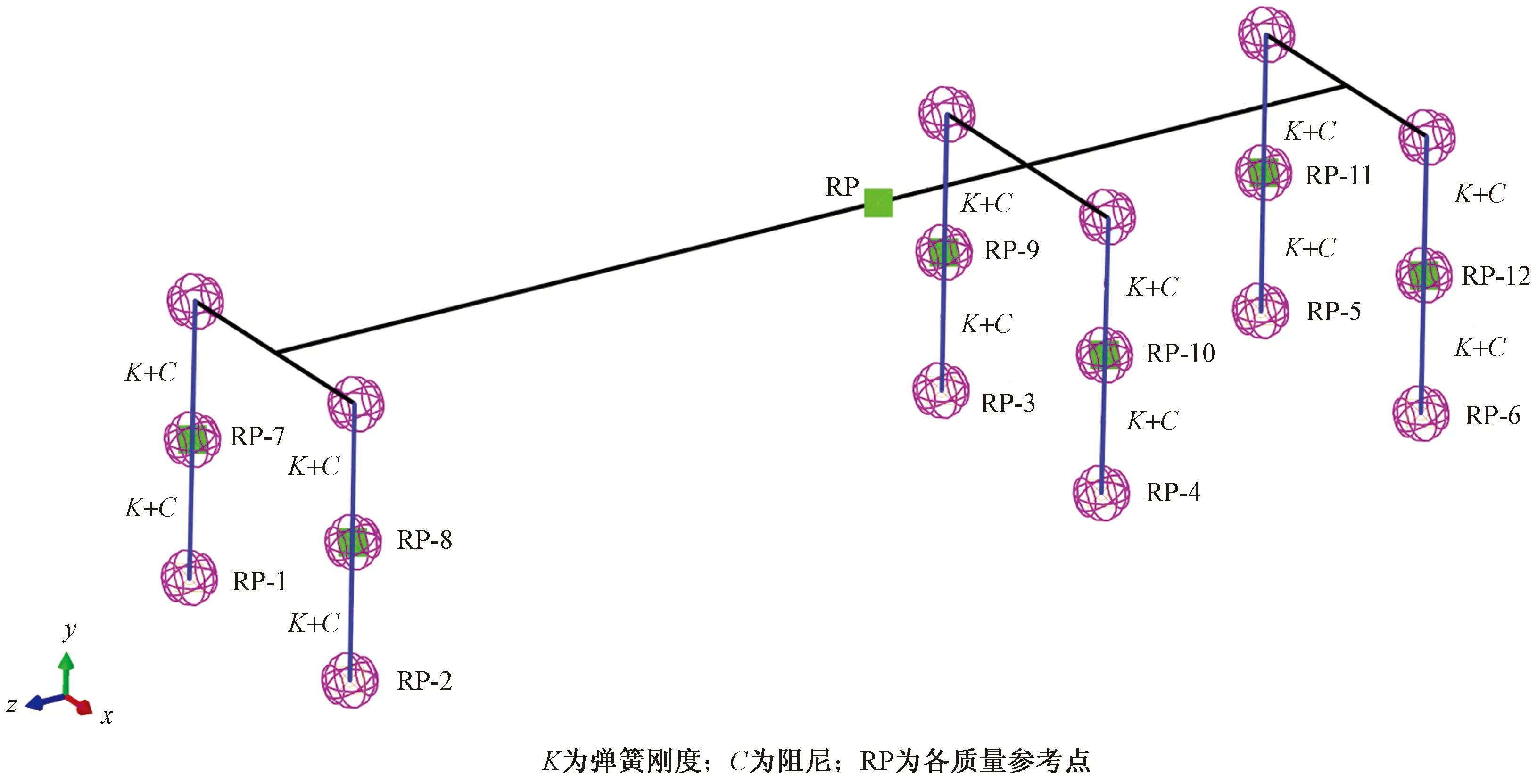
图10 车辆的有限元模型Fig.10 Finite element model of the vehicle

为了保证车轮与桥面的竖向位移协调，车轮与桥面间的接触关系为通用接触，其法向接触为硬接触，切向接触为罚接触，摩擦系数为0.2。

5 动力冲击系数

动力冲击系数μ在桥梁设计中用以表示车辆通过桥梁时对桥梁结构产生的竖向动力效应增大系数，是评估桥梁状况的重要参数，其定义为

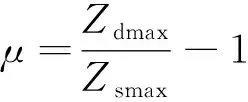
(9)

式(9)中：Zdmax为最大动位移；Zsmax为最大静位移。

因现行规范中尚无单独考虑管翼缘组合梁冲击系数的计算，故采用《公路桥涵设计通用规范》(JTG D60—2015)中利用桥梁的基频计算的动力冲击系数，计算公式为

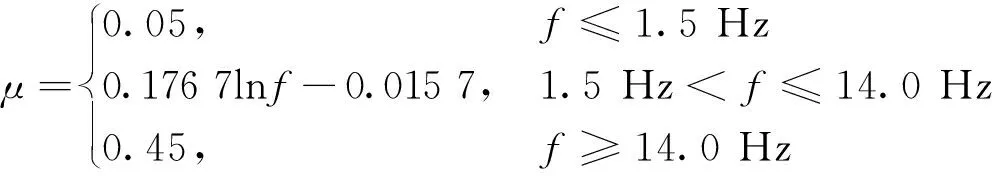
(10)

式(10)中：f为桥梁结构的基频。

利用有限元方法计算了管翼缘组合梁、等效工字钢梁和等效混凝土梁的自振基频，然后用式(10)计算了3种类型的动力冲击系数，其结果如表4所示。

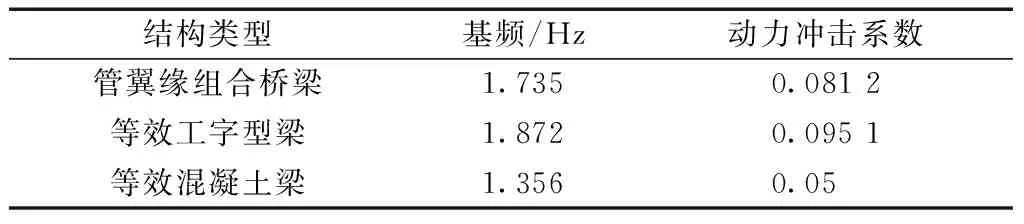
表4 各类桥梁有限元基频和动力冲击系数

6 计算结果分析

6.1 不同车道对动力冲击系数的影响

桥面共分了5个车道，如图 7所示，在路面平整度光滑情况下，车辆以60 km/h的速度在不同车道上行驶，经过计算得到图11所示的位移时程曲线。

由于桥梁与墩柱盖梁是斜交的，边跨梁不等长，所以车辆在车道1、2、4、5上行驶时，A点和B点的动力冲击系数较小，敏感性较低，不利于车桥耦合作用的分析。只有车辆在车道3上行驶时A点和B点处的动力冲击系数最大，敏感性高，也具代表性，如图12所示，因此选用车道3作为研究对象。

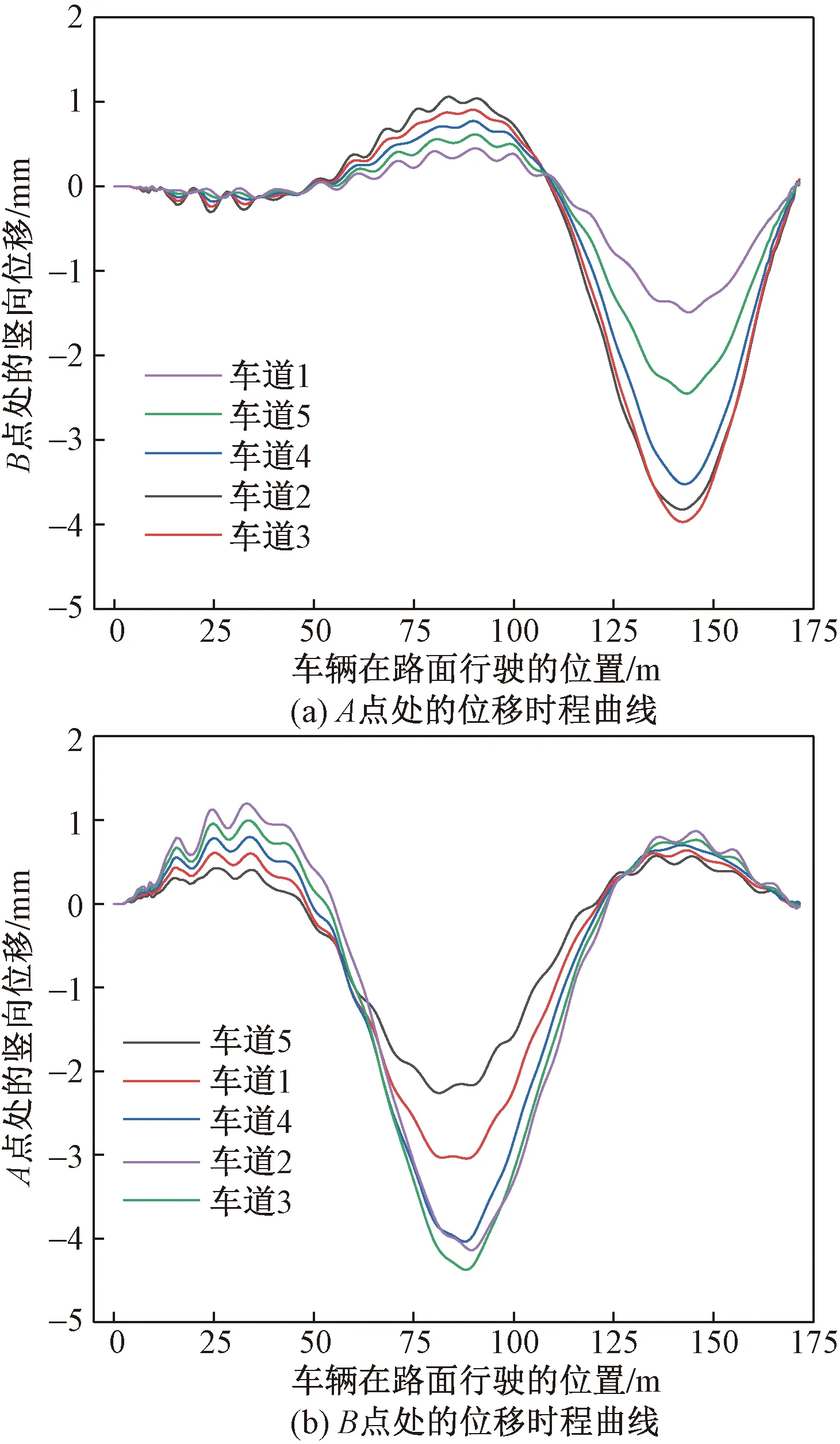
图11 车辆在不同车道时的位移时程曲线Fig.11 Displacement time history curves of vehicles in different lanes

6.2 路面平整度对桥梁的动力影响

在桥面不同的平整度的情况下，车辆以 60 km/h 的速度在桥面行驶时，经过计算得到了A点和B点的位移时程曲线，其结果如图13所示。

通过对比，可以看出路面平整度对桥梁的影响比较大，桥梁的跨中最大挠度随路面平整度的等级呈正相关。例如，A等级路面是光滑路面的1.005倍，而D等级路面是光滑路面的1.336倍，可见路面平整度是桥梁建设中不可忽略的一部分，以及在今后的桥梁养护中也是重点考虑的对象。

表5为A点与B点在等效静力荷载作用下的最大位移，利用式(9)求得了各种路面等级下的动力冲击系数，并与《公路桥涵设计通用规范》(JTG D60—2015)中的式(10)求得的动力冲击系数进行对比分析，其结果如图14所示。

从图14中可以看出，路面平整度为光滑和A等级的情况下，动力冲击系数的计算值小于规范的设计值；当路面平整度等级为C级、D级的情况下，动力冲击系数的计算值要比规范设计值大，分别为光滑路面的2.53倍和4.81倍，呈几何倍数增长；路面平整度为B级的情况下，动力冲击系数的计算值与规范中采用有限元法获取基频后求得的动力冲击系数比较接近，相差为12%，但是还是偏大于规范中计算的结果，以后对此种类型桥梁设计时，应对通过规范获得动力冲击系应予以修正。

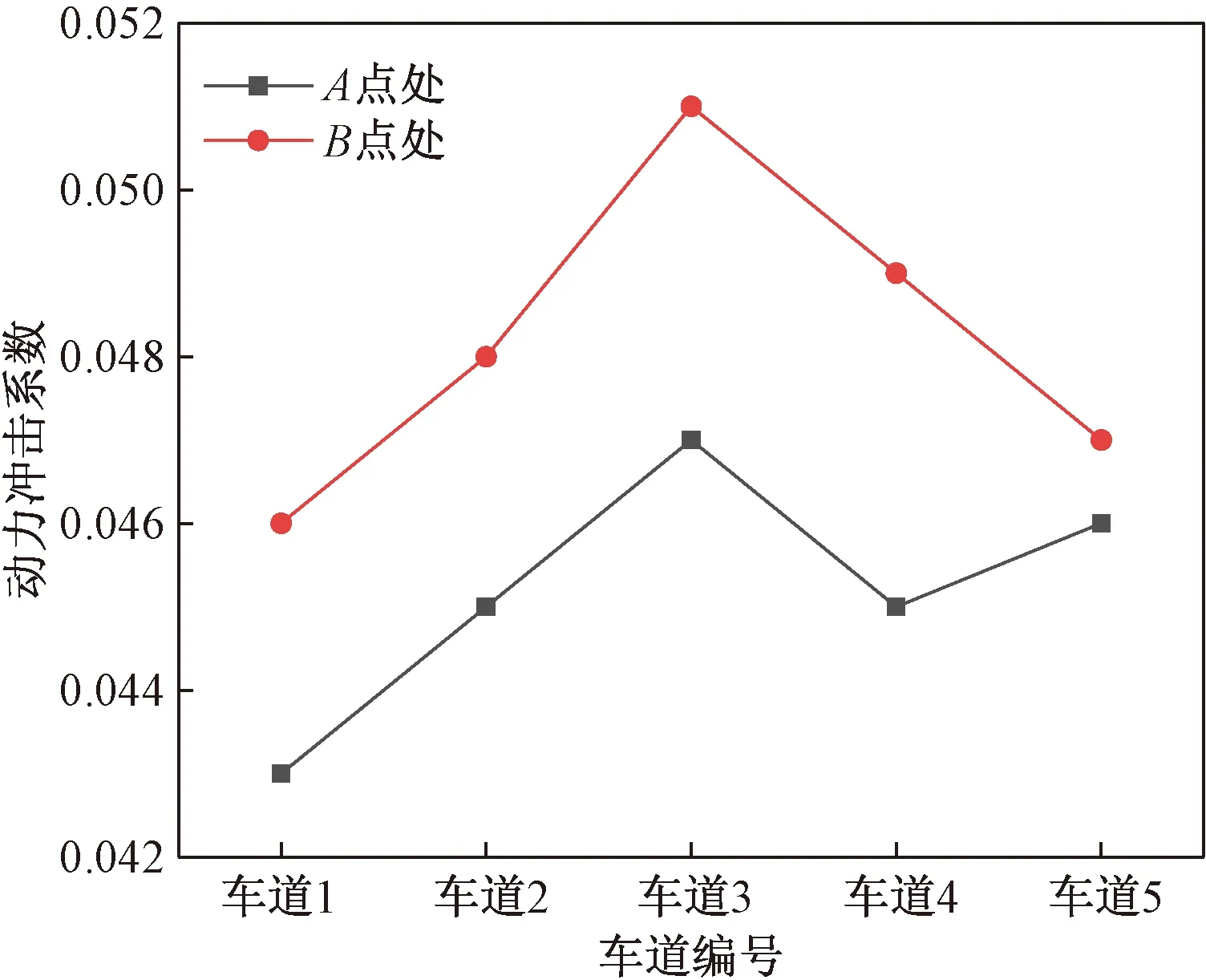
图12 车辆在不同车道行驶时的动力冲击系数Fig.12 Dynamic impact coefficient when the vehicle is driving in different lanes

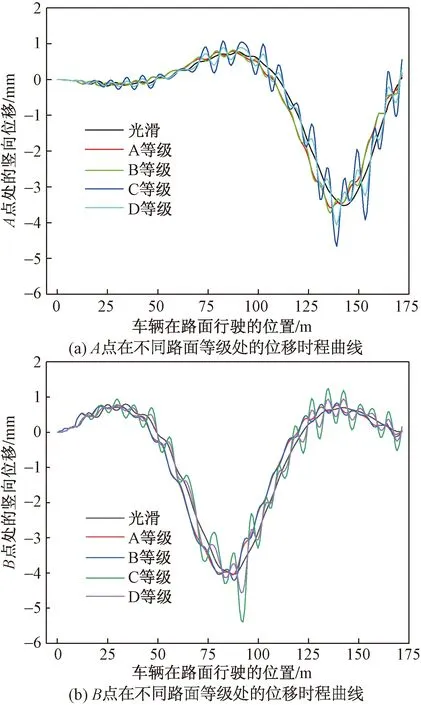
图13 路面等级不同时的位移时程曲线Fig.13 Displacement time history curve with different road grades

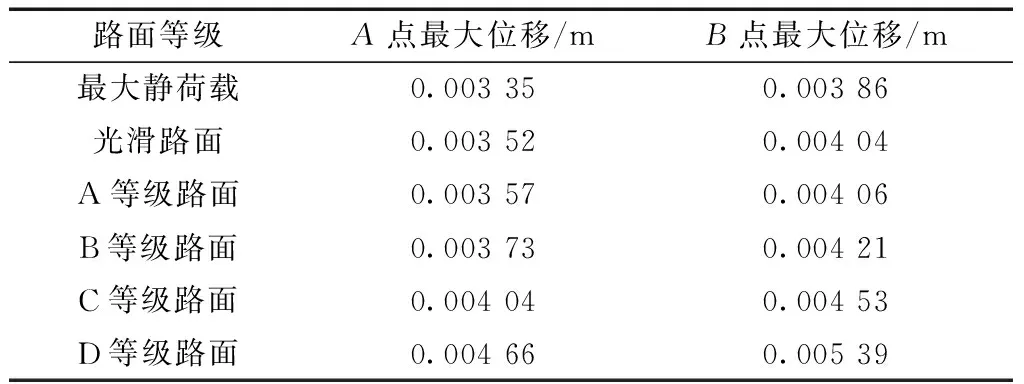
表5 A点和B点处的竖向最大静位移

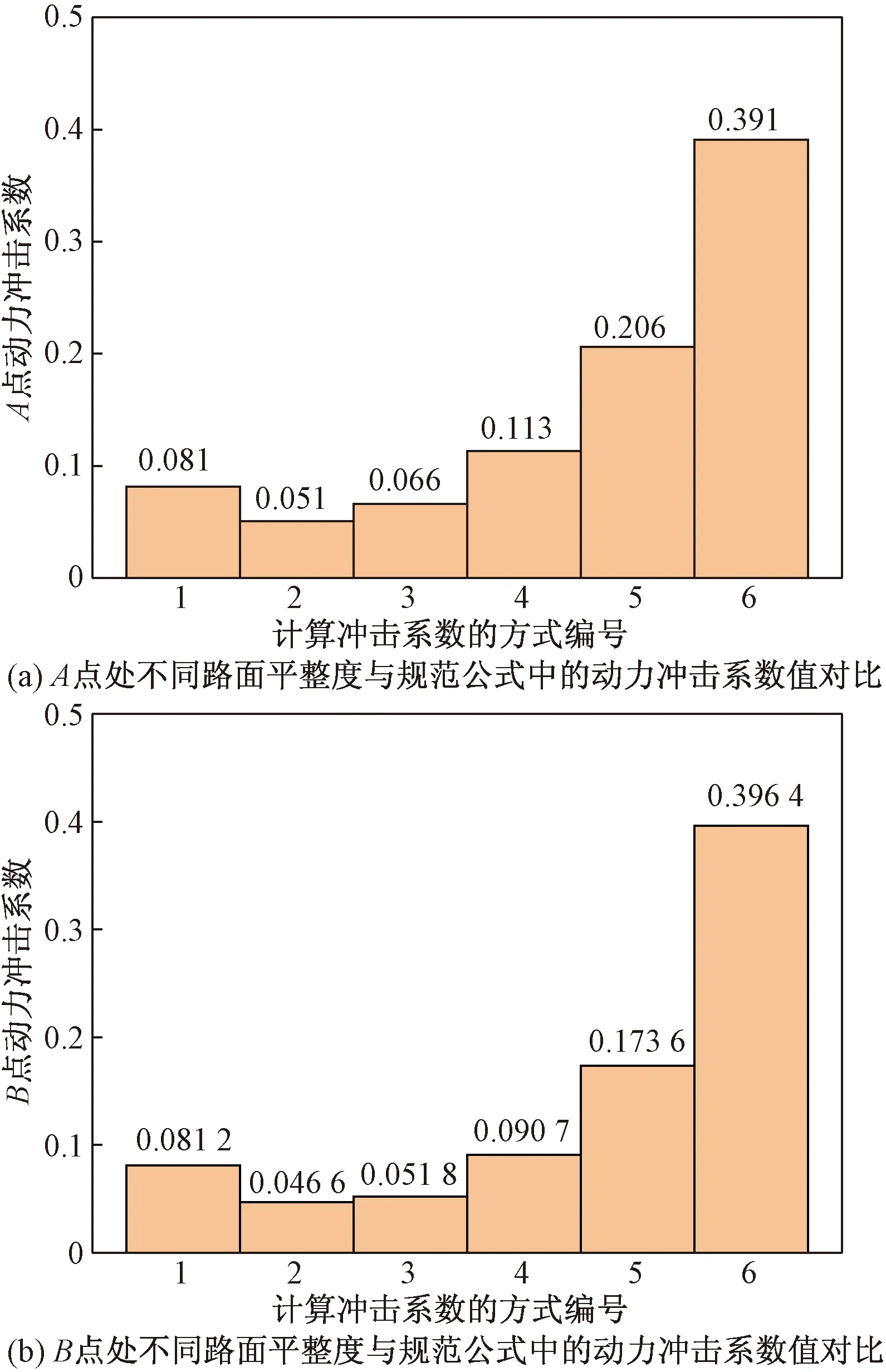
1为《公路桥函设计通用规范》(JTG D60—2015)中计算的值； 2为光滑；3为A等级；4为B等级；5为C等级；6为D等级图14 各种路面平整度与规范公式计算的动力冲击系数Fig.14 Variety of road surface roughness and dynamic impact coefficient calculated by standard formula

6.3 速度对桥梁的动力性能影响

在路面等级为B的情况下，车辆以20 km/h的梯度，从40 km/h的速度增加到120 km/h的速度，经过计算得到了图15所示的各种速度的竖向位移时程曲线，当车辆行驶速度为40～60 km/h时，竖向位移曲线较为平缓，当速度为80 km/h时，开始有明显的波动。图16为参考点B处不同速度的竖向加速度的时程曲线，通过对比了各种速度下的竖向最大加速度值，如图17所示，当速度为60 km/h时B点处的竖向加速度最小，原因是车辆速度和路面平整度的因素造成车辆竖向振动频率与桥梁竖向振动的固有频率相差较大，避开了共振现象，但是随着车速的增加，两者的频率逐渐接近，桥梁的加速度最大值也随着增加，振动频率加大，长此以往将会损坏桥梁结构，降低桥梁的预期寿命，所以车辆的速度应该限制在一定的范围内，如80 km/h以内的速度是相对安全的。

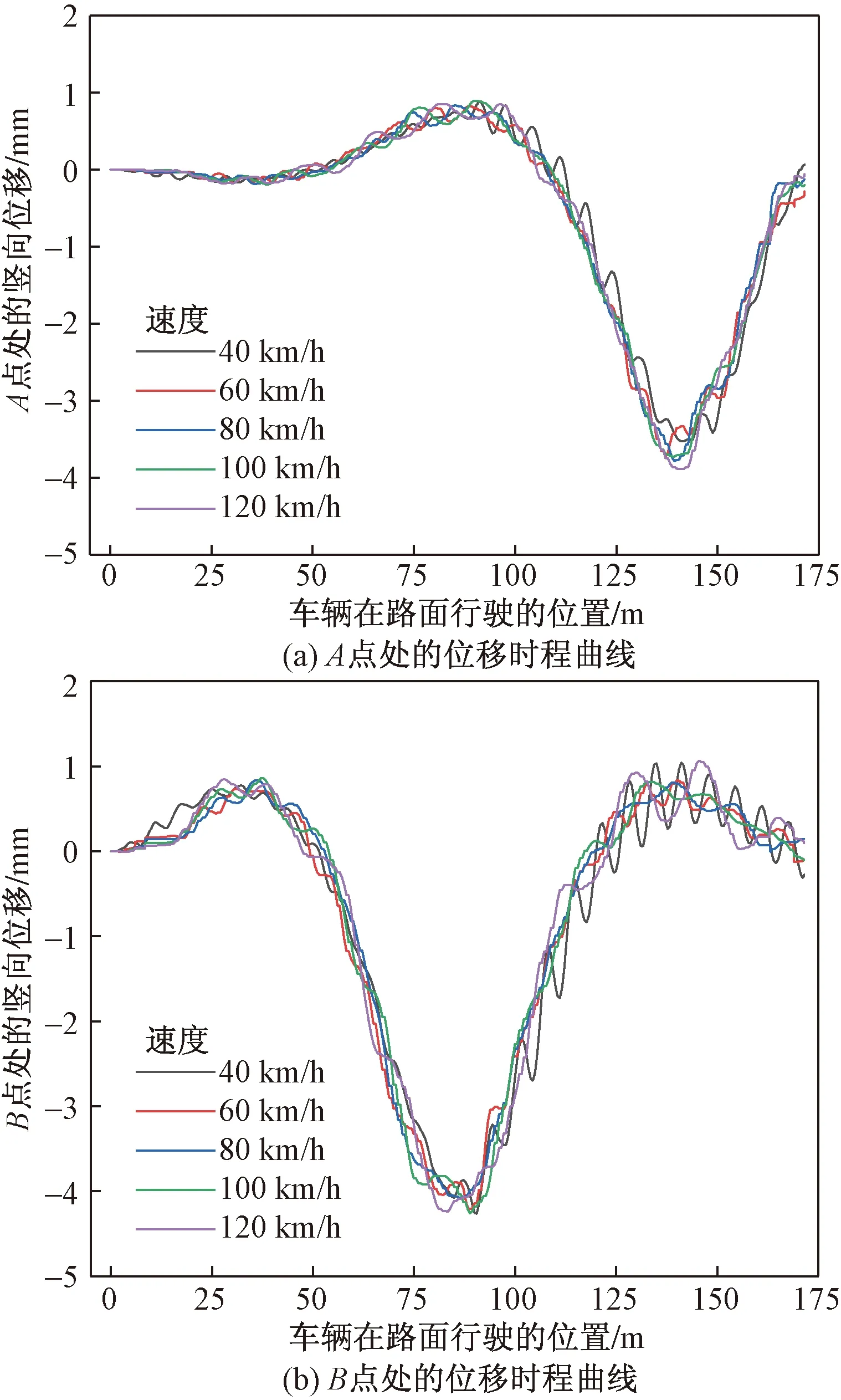
图15 车辆在B等级路面下不同速度的时程曲线Fig.15 Time-history curves of vehicles at different speeds on B-grade roads

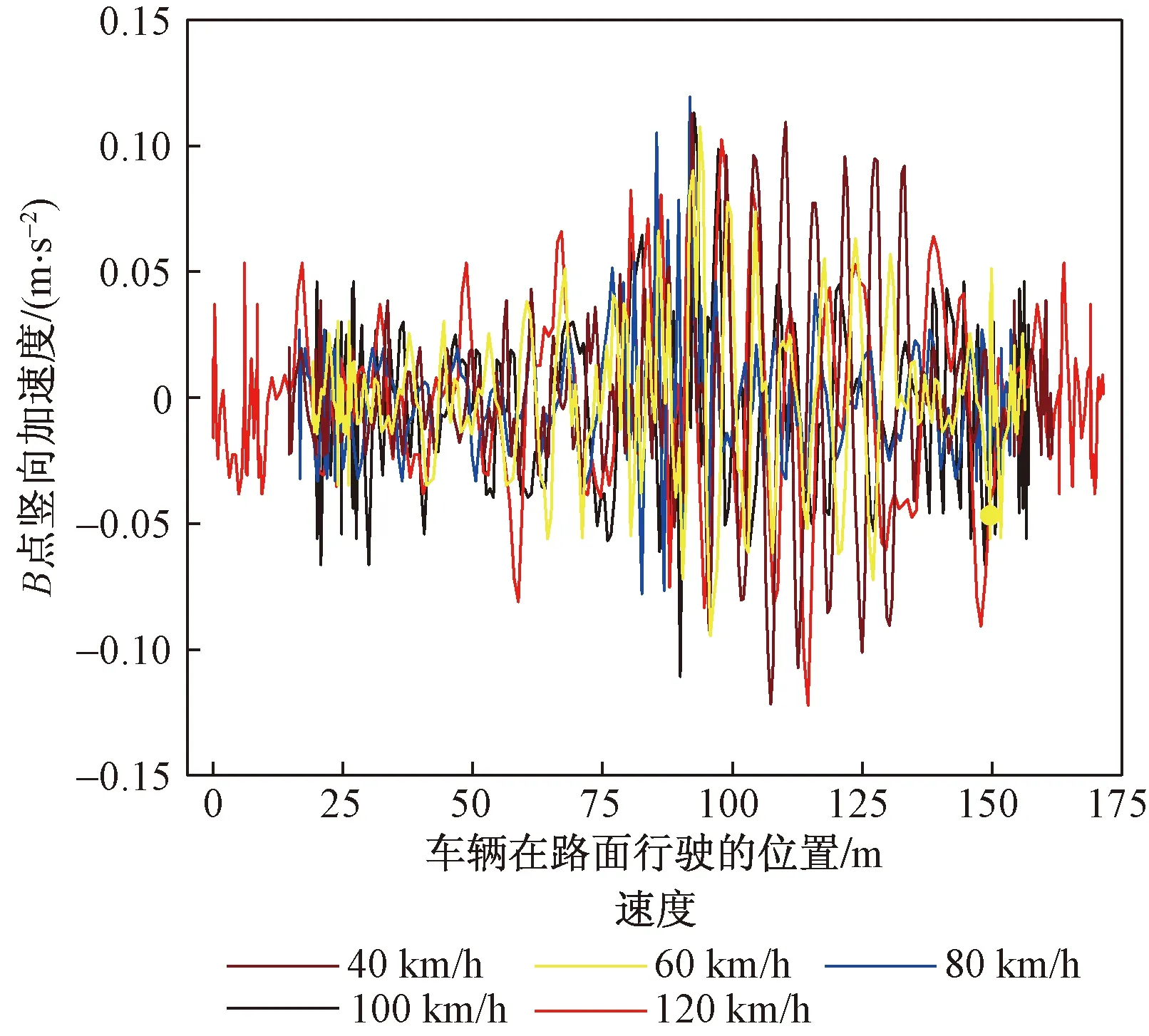
图16 车辆在B等级的路面下不同速度对应的加速度的 时程曲线Fig.16 The time-history curve of the acceleration of the vehicle at different speeds on the B-level road

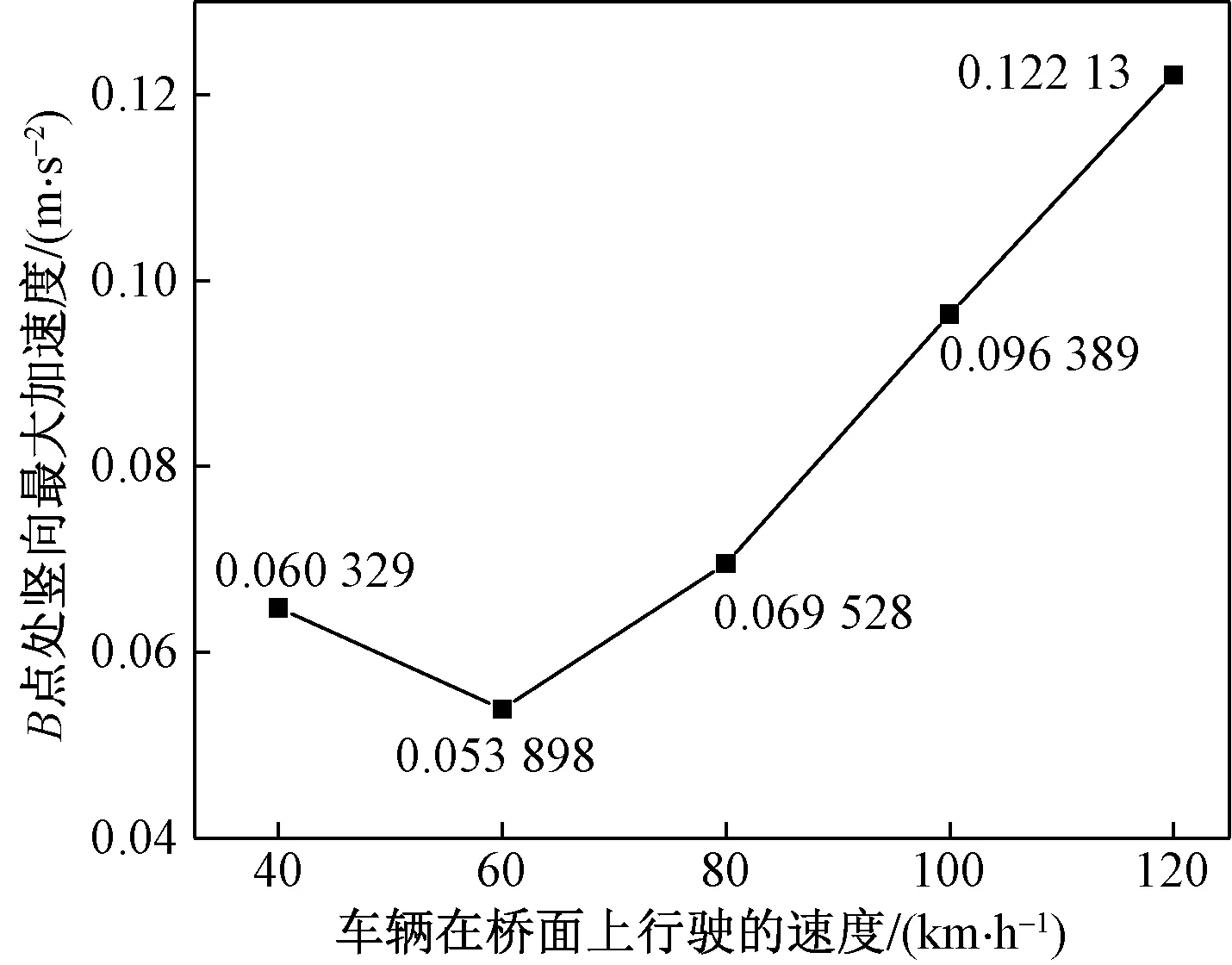
图17 各种速度对应的最大加速度Fig.17 Maximum acceleration corresponding to various speeds

6.4 载重对桥梁的动力性能的影响

当在路面等级为B且车速保持在60 km/h时，以每10 t的梯度，使车辆载重从25 t增加到105 t行驶时，经过计算得到其位移时程曲线如图18所示。由于桥梁的主要材料是钢材，且都在弹性变化范围内，随着载重量的增加，跨中的位移呈线性增长，如图19所示。

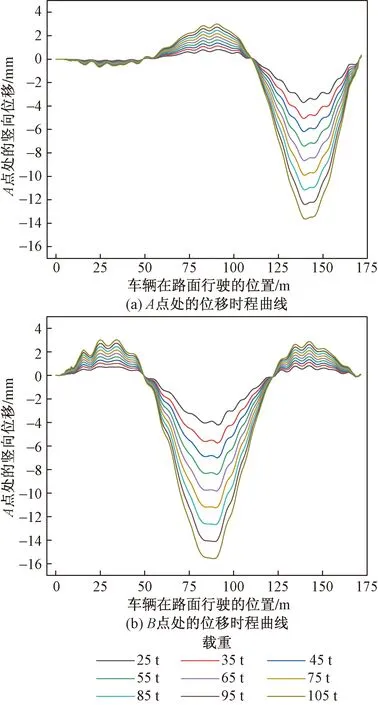
图18 不同载重的情况下的位移时程曲线Fig.18 Displacement time history curve under different load conditions

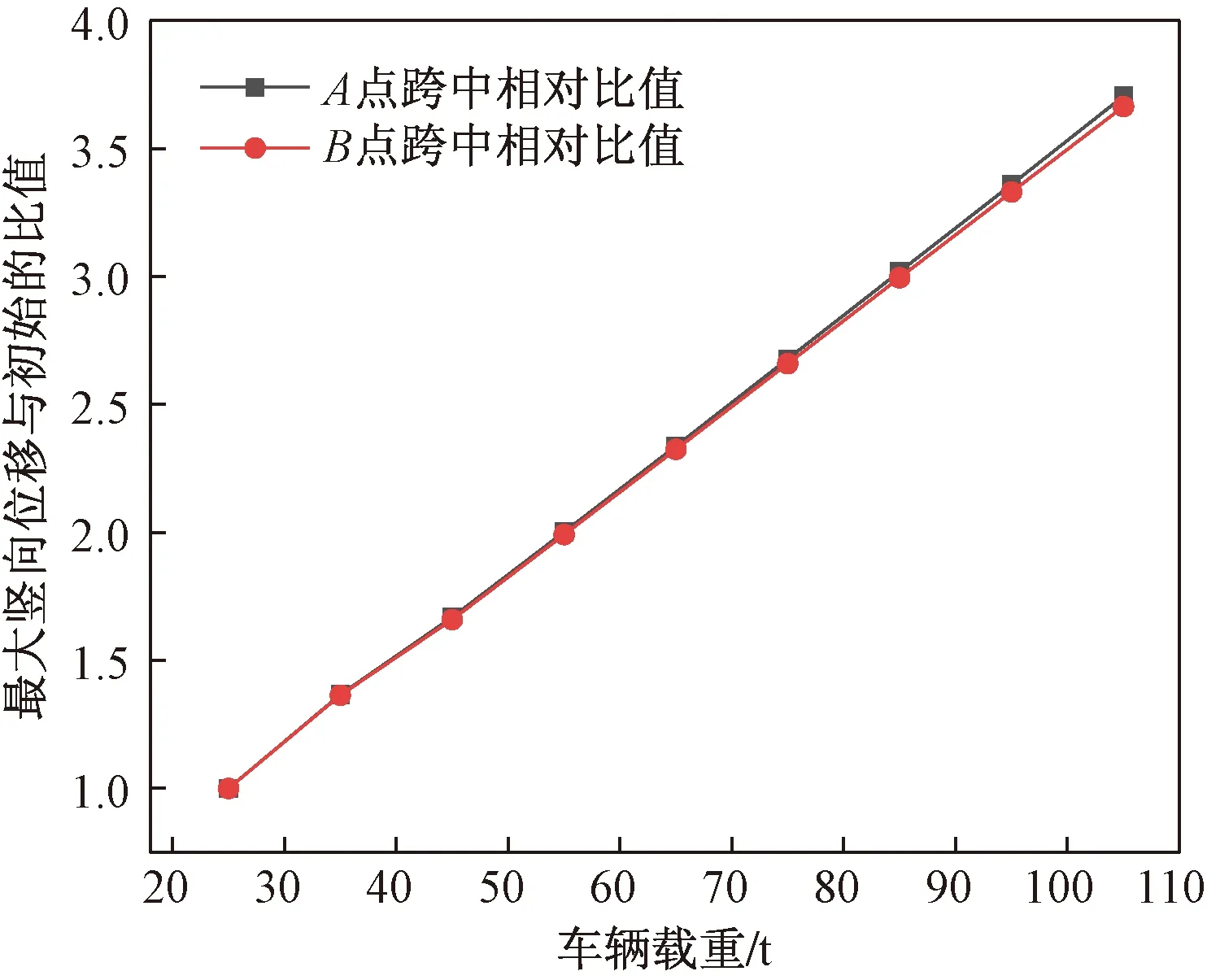
图19 竖向最大位移与初始值的比值Fig.19 Ratio of the maximum vertical displacement to the initial value

由于规范中规定桥梁的跨中挠度最大为 11.2 cm(即L/500)，其中L为桥梁的跨度，当车辆的载重超过75 t时，跨中位移就超过了规范中的规定的最大挠度，而此桥梁限重是30 t，有足够的荷载富裕度，但需要在后期的使用中，严格限制它的载重。

6.5 上翼缘钢管内混凝土等级和含钢率对桥梁的动力性能影响

在路面等级为B的情况下，车辆以60 km/h的速度行驶时，改变管翼缘内混凝土的等级和管翼缘的含钢率，经计算得到了图20、图21所示的位移时程曲线，可以看出，混凝土等级和含钢率几乎对桥梁结构没有影响，结论与文献[23]中静力荷载作用下的结论相一致，因此，混凝土等级和翼缘含钢率在设计时只要符合规范要求就行，选取合适的含钢率和混凝土等级，这样可以提高工程项目的经济效益。

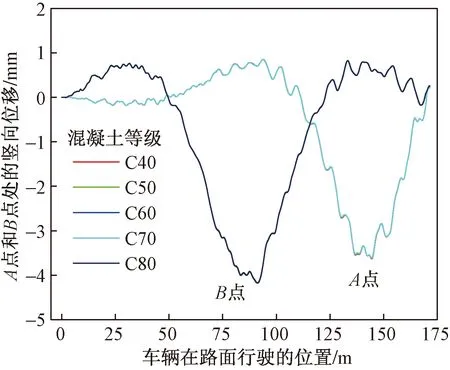
图20 不同等级混凝土的位移时程曲线Fig.20 Displacement time history curves of different grades of concrete

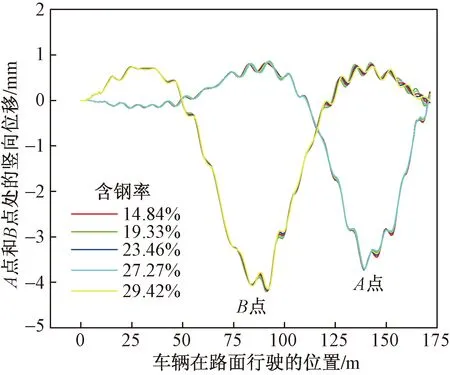
图21 含钢率不同时的位移时程曲线Fig.21 Displacement time history curve with different steel content

6.6 不同类型桥梁的动力性能对比

在路面等级为B的情况下，车辆以60 km/h的速度分别通过等效工字型钢梁桥、混凝土梁桥时，经计算得到了各自与A点和B点相同位置处的位移时程曲线，并与相同条件下管翼缘组合梁计算得到的位移时程曲线进行了对比，其结果如图22所示。

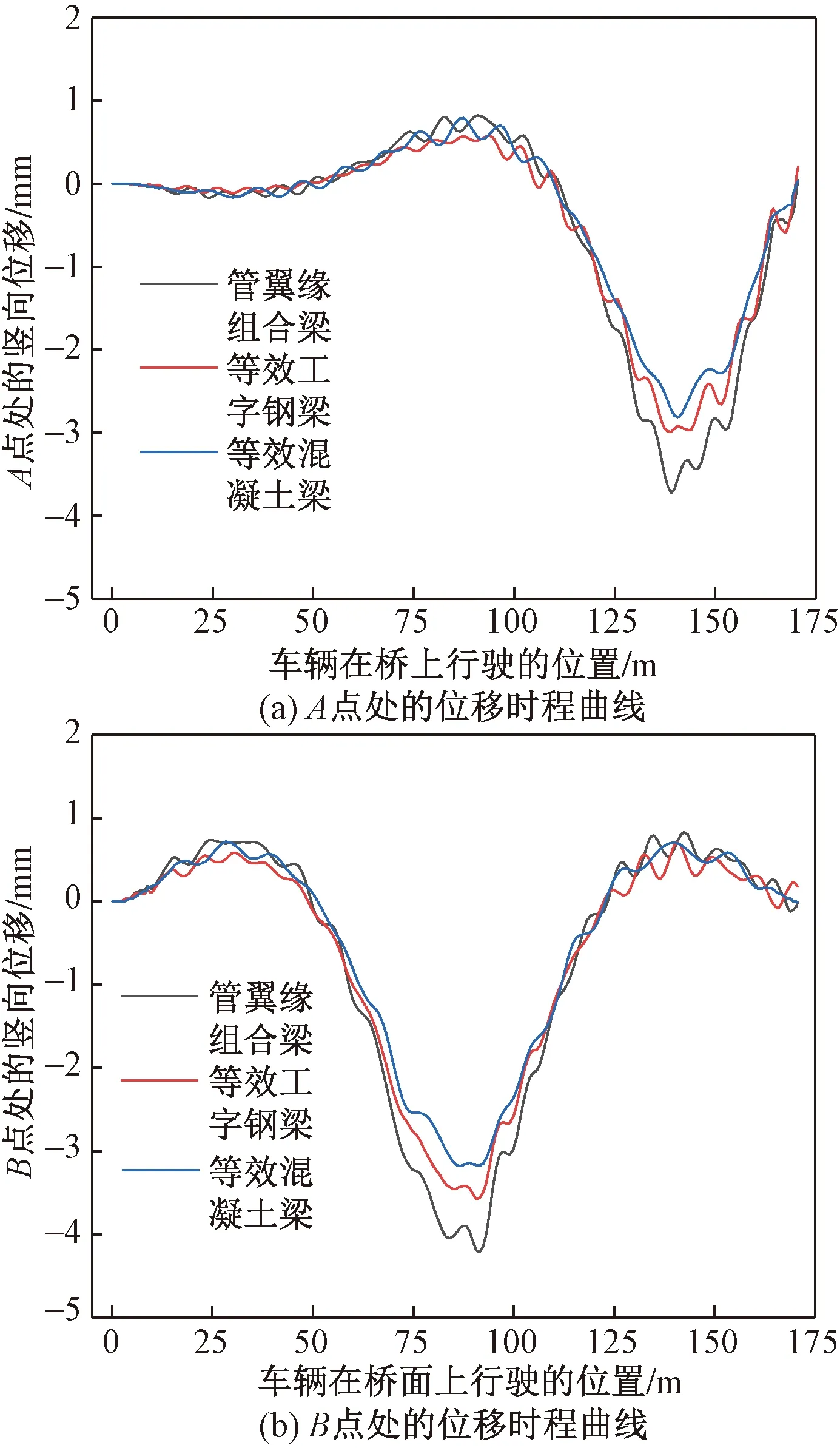
图22 不同类型梁的位移时程曲线的对比Fig.22 Comparison of displacement time history curves of different types of beams

可以看出，钢管翼缘组合梁桥跨中挠度最大，混凝土梁桥的挠度最小，且三者的跨中挠度的比为1∶0.87∶0.75，其主要原因是在同等抗弯刚度下，管翼缘组合桥用钢量比较少，自重轻，整体弹性模量较小，在相同荷载的作用下，其竖向位移变化较大，而且对相邻梁的影响比较大，进而使得扭转变形增大，所以在此类桥梁的设计中，应增大其横向刚度。

7 结论

采用ABAQUS有限元软件，建立了计算跨径为163 m的三跨连续管翼缘组合梁桥的有限元模型，对路面平整度、车速及车重等因素影响下的动力性能进行了计算，分析了路面平整度、车速、车重、上翼缘内混凝土等级和含钢率对管翼缘组合梁桥的动力响应，并且和抗弯刚度相同的工字梁桥和混凝土梁桥的动力性做了对比，得出如下结论。

(1)冲击系数与路面平整度的等级呈正相关，在路面平整度为B的情况下，经计算的动力冲击系数与规范中给定的公式计算的冲击系数比较接近，但是有12%的差别，所以计算此类桥梁的动力冲击系数时需要对规范中的公式进行修正。

(2)车辆行驶速度和载重对管翼缘组合梁桥的影响比较大，随着车辆的速度增大桥梁的振动幅度也随之增大，但速度为60 km/h时的振动相对较小，主要是因为车辆速度以60 km/h行驶时的振动频率与桥梁的竖向自震频率相差较大，并且车辆载重与跨中的挠度呈线性增长，需要在后期营运中控制车辆载重来保护桥梁，所以车速和载重的影响是研究管翼缘组合梁非常重要的动力因素。

(3)上翼缘钢管内的混凝土等级和含钢率对桥梁的动力响应基本没有影响，因此建议在今后的设计中只要满足规范中的要求即可。

(4)在抗弯刚度相同的情况下管翼缘组合梁与等效工字钢梁和混凝土梁相比，其跨中挠度的动力响应比较大，主要的因素是其重量和整体弹性模量较小，但这样将会造成桥梁的扭转作用较大，所以在以后设计此类型桥梁时需要增大其横向刚度。