“工资中位数问题”的方案分析与设计*

王鹏宇 张艳硕 李烨龙

北京电子科技学院，北京市 100070

0 引言

姚氏百万富翁问题［5］由华裔计算机科学家、图灵奖获得者姚期智［1］先生于1982 年首次提出：存在2 个争强好胜的富翁Alice 和Bob，他们如何在不暴露各自财富的前提下比较谁更富有？ 后来该问题演变成安全多方计算［2］。 随着网络技术与计算能力的不断进步，人们越来越注重个人隐私的保护，如今对用户隐私的保护成为了计算的基本要求，安全多方计算正是在这样的环境下引起人们越来越多的关注。 由百万富翁问题发展而来的安全多方计算是指两个或多个互不信任的用户在无可信第三方的情况下，如何安全的计算一个约定函数，同时还要保持各自数据的安全性。

安全多方计算的基本概念［2］是“一组参与者希望共同计算某个约定的函数；函数的输入参数有多个；每个参与者提供函数的一个输入；每个人都知道这个函数的值；除了函数的输出外，没有人知道其他参与者输入的信息”。 一个安全多方计算协议，如果对于拥有无限计算能力攻击者而言是安全的，则称作是信息论安全的或无条件安全的；如果对于拥有多项式计算能力的攻击者是安全的，称为是密码学安全的或条件安全的。 已有的结果证明了在无条件安全模型下，当且仅当恶意参与者的人数少于总人数的1／3 时，安全的方案才存在。 而在条件安全模型下，当且仅当恶意参与者的人数少于总人数的一半时，安全的方案才存在。

安全多方计算不同于传统意义上的密码学，传统意义上的密码学主要研究的是在不安全的媒体上提供安全通信的问题，是指在信息传送过程中防止信息泄露或者被篡改，其加密机制属于传统密码学的范畴。 而安全多方计算主要研究的是系统内部各参与方协作计算时各自数据的隐私保护问题，更加偏向于网络计算。 安全多方计算分为两种模型，半诚实模型和恶意模型。 半诚实模型是指，所有参与者都是诚实，或者半诚实的，相互之间没有勾结，不存在主动攻击，完全按照协议的规程执行，不会中途退出或者篡改运行结果，但是参与者可以保留运算过程中所有的中间结果，以期望在运行结束后推断出其他用户的输入信息。 恶意模型则是指有恶意参与者的模型，其中的攻击者是主动的，可能会不按照协议的流程执行、随意终止协议的运行，也可能会修改协议的中间结果或者与其他参与方进行勾结。 本文所讨论的针对“工资中位数”问题的解法主要是在半诚实模型的基础上进行计算的。

安全多方计算理论［12］主要研究参与者间的协同计算及隐私信息的保护问题，其特点包括输入隐私性、计算正确性及去中心化等特性。 在隐私保护被不断提及的当下，安全多方计算研究取得了极大的进步。 密码学家研究了各个应用领域中出现的安全多方计算问题，其中包括保密科学计算、保密计算几何、保密数据挖掘等问题。安全多方计算在电子选举、门限签名以及电子拍卖等诸多场合发挥了巨大的作用，成为了这些设计得以实施的密码学基础，为实现数据的可控共享做出了极大的贡献。

基于安全多方计算的工资中位数问题在信息安全实践中具有重要的实际意义。 在日常生活中，工资无论对于个人或者公司来说都是极为隐秘和重要的数据。 如果员工想要知道自己的工资在公司中处于什么样的水平，就需要计算公司员工的工资中位数。 由于员工和公司之间通常都签有保密协议，因此需要进行工资中位数问题的保密计算。 除此之外，工资中位数问题还具有很重要的数学意义。 如何利用纯数学的知识来进行工资中位数的保密计算，这需要借助安全多方排序，同时还需要设计一个可靠的中位数计算函数来进行计算，达到安全的同时保证其简易可行。

工资中位数问题属于安全多方计算平均工资问题的衍生问题，作为统计学与经济学的结合，相较于平均工资，更能贴近普通民众的实际生活水平，本文在研究其解法的同时深入讨论该问题背后隐藏的安全性问题，即存在的信息泄露的隐患，并针对该问题设计安全方案。 本文针对工资中位数问题进行深入分析阐述，借鉴了李烨龙等［9］关于平均工资问题的研究，并结合了利用最小堆求无序数组［11］中位数的算法，引用了石磊等［3］关于信息秘密比较的研究，采用了秘密比较协议［4］的计算方法，达成了在确保安全性以及用户工资不被泄露的同时计算工资中位数的目的。

1 工资中位数问题

工资中位数问题在安全多方计算领域属于平均工资问题的一种延伸。 工资中位数问题来源于平均工资问题，首先我们将对平均工资问题进行简单介绍。

1.1 平均工资问题

现假设有四名员工Alice、Bob、Carol 和Dave四个人在一家公司工作，他们均签署了公司的保密协议，即他们不能向其他人透露自己的工资，但是他们每个人又想了解彼此的工资情况，现场无仲裁者。 在这种情况下，最能够简单直白地作为衡量自己工资标准的就是四个人的平均工资，在这种情况下计算四人的平均工资就是安全多方计算平均工资问题。

1.2 工资中位数问题

本小节将具体阐述工资中位数问题，工资对于个人和公司来说是极其隐私的数据。 很多公司的工资信息十分的隐蔽。 为了不让工资信息外泄，员工必须签署工资保密协议，每个人不得透漏自己的工资，但是有些员工想了解自己在公司的工资处于什么层次。 安全多方计算中的安全多方排序［6－8］就能解决这个问题，通过一个公认的函数秘密的计算工资中位数，每个人就都可以根据工资中位数来判断自己在公司中的层次。现假设有n名员工在一家公司工作，他们均签署了公司的保密协议，即他们不能向其他人透露自己的工资，但是他们每个人又想知道自己的工资在公司处于什么样的水平，现场无仲裁者。 在这种情况下，只需要一个能够安全计算出工资中位数的函数，就可以计算出工资中位数，从而每个人都可以根据工资中位数来分析自己在公司的工资处于什么水平。

在经济学中，工资中位数用来描述收入分配差异程度，因为某地区的人均收入因贫富的差距可远远大于收入中位数，而收入中位数则可以将这种差距反映出来。 而在统计学中，中位数［10］是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，相较于平均数，中位数不易受数据中极端数值的影响，但是当中位数与安全多方计算结合到一起，就出现了如何在不暴露参与者信息的情况下计算出中位数的难题。 下文将根据上述问题来设计安全多方计算中的“工资中位数问题”解决算法，分析其中的安全性问题并设计安全方案。

2 工资中位数问题解决思路

本节将介绍解决安全多方计算工资中位数问题的一般设计思路，并在对现有的解决方案与解决思路进行解释。

2.1 前提条件

为了深入探索该安全多方计算工资中位数问题的解法，必须先探讨一些前提条件，为了寻求方案的一般性，在这里直接讨论针对n个人的情况。

我们在文献［9］的基础之上研究这个问题，文献［9］中有两个前提分别如下：

前提1：模型为半诚实模型，每个人提供自己的工资信息时不能撒谎。

因为在这n个人中，如果有一个人对自己的工资数据撒谎，那么工资中位数的计算就会在该环节出现错误，那么整个协议就会无效［9］。

前提2：协议中没有可信第三方。

也就是说，在该协议中不存在一个第三方来协助计算，全部的过程都是只有参与者来进行［9］。

在上述前提之下，如果存在除参与者之外的敌手对该协议进行攻击，那么同样会出现安全风险。

2.2 已有解决方案

本小节先给出现有的解题方案（简称为方案一），方案的具体步骤如下：

（1）M1与M2先进行第一轮比较。M1与M2将自己的工资随机分成n－2 份，并分别用Mj（j＝3，4…n）的公钥加密，用自己的私钥签名，并分发给相应的人。

（2）Mj（j＝1，2，3，4，5…n）收到M1与M2的数据以后进行比较，将两者相减，得出的两个结果（正负不同）根据两者的大小，将数据再用M1，M2的公钥加密，用自己的私钥签名后，发给M1，M2。 （例如M1的数据为123，M2的数据为456，则将－333 发给M1，将333 发给M2。 ）

（3）M1，M2收到数据后，将收到的所有数据相加，得出的结果如果M1为正，M2为负，则说明M1的工资比M2高，反之则M2比M1高。

（4）接下来令M1，M2中大的使用序号1（例如，M2比M1大，则M1与M2交换序号，M1序号为2，M2序号为1）并且交换公钥与私钥（即身份交换，M1变为M2，M2变为M1）。 例如，M1大于M2，则不需要进行身份交换过程，如果M1小于M2，则需要身份交换。 然后继续让M1与M3，M4，M5…Mn重复进行比较过程，以及身份交换过程。

（5）M1完成一轮比较后（此时工资表第一位已经排出来，但是理想情况下只有自己知道自己是工资表第一位，非理想情况即，例如Mn的工资为最大的，M1与Mn完成比较后进行了身份交换，此时的M1与Mn都知道了原Mn的工资是最大的）。M2进行下一轮比较，重复比较过程与排序过程。

（6）最后直到Mn－1完成排序后，整个过程结束。 理想情况下只有每个人自己知道自己的工资表排名，所以只有工资排名处在中位数位置的，才知道自己的工资为中位数。

（7）所有人将自己的工资随机分为n－1份，（工资处在中位数位置的人可以撒谎将工资乘以2 后再随机分为n－1 份）（若n为奇数，则工资中位数位置是（1／2）*（n ＋1）， 如果n是偶数， 则工资中位数位置为 （1／2）*n与（1／2）*n ＋1）。 分别用Mj（j＝1，2，3…n）（除自己以外）的公钥加密，用自己现在的私钥（即身份交换后的私钥）签名，发给Mj。

（8）所有人完成分发后，M1将自己收到的n－1 个数据加和，减去自己的工资后。 将得到的结果发给下一个人，下一个人收到数据后，将数据与自己之前收到的n－1 个数据加和，减去自己的工资，将得到的结果再发给下一个人。

（9）重复此过程，直到所有人都将自己的工资减去。 此时最后一个人得出工资中位数。（如果n为奇数，则得出的是工资中位数，如果为偶数，则该数除以2 得到中位数）

但是此方案存在一种致命的问题，就是信息泄露问题。 在比较大小过程中，比较完成后，比较结果发回给M1，M2， 此时M1，M2都知道了对方的工资数据，如果两人中有一个人试图泄露对方的工资数据，那么整个协议就是失败的。 而且这个方案与保护工资隐私的原则相悖。

3 工资中位数问题方案分析

方案一的设计思路表面上可以解决工资中位数问题，但是该方案在实际操作中还是存在着不可忽视的安全问题，本小节将揭示其存在的问题，在对其进行分析同时给出问题解决思路。

3.1 存在问题

方案一中，两名用户首先将工资数据进行拆分加密后发放给其余人，在此处对工资数据进行的加密会保证即便他人将信息截取，也不能解密得出拆分前的结果。 随后其他人对收到的两份数据进行比较，将结果再加密后发还两名用户。但是方案一实际上并没有满足安全多方计算中的安全要求，在工资进行两两比较时，比较完成后，两名用户对收到的所有返回数据进行加和得出的是两名用户的工资差值。 两名用户就会得知对方的工资数据信息。 这就存在信息泄露隐患，参与比较的两个人都会知道对方的工资。

虽然方案一的去中心化和数据发送加密满足问题需求，同时没有第三方的参与。 但是存在工资泄露的隐患，如果两个人中存在一人将对方的工资信息泄露，整个协议就会暴露出安全隐患。 且方案一的解决步骤过于臃肿繁琐，不利于理解和计算。

3.2 问题解决思路探讨

在对方案一进行安全性分析后，本小节将针对以上原始方案一中存在的安全问题进行探讨并给出改进的方案思路。 我们在对中位数问题进行研究的时候发现了另一种更加安全的工资比较方法，该方法有着很高的安全性同时还具有一定的密码学数学基础。 本小节将根据此方法衍生的改进思路进行简单的介绍。

由于方案一安全性无法保障，在工资信息比较环节存在工资隐私数据泄露问题，但是方案一中对工资信息进行非对称加密的设计思路以及中位数计算的思路可以借鉴，因此新方案将沿袭方案一中的“中位数计算”与“非对称加密”的方法，使计算过程更加安全可靠，将方案流程上的存在的安全风险进一步降低，增强其安全性。

借助取余数的方式对工资进行比较。 假设有两个人A、B，他们的工资分别是a、b（假设工资区间为1000～2000，且两人都可以使用计算机辅助计算），协议开始前，B 生成一对RSA 密钥。首先，A 选取一个大随机数x， A 用B 的公钥对随机数x加密，得到密文m。 A 把m减a的值发给B，那么B 实际接收到的数就是m-a。 接下来，B 尝试用私钥来恢复x。 由于B 不知道a是多少，于是B 只能枚举所有1000 到2000 之间的整数，用私钥对1000 ～2000 这1001 个数分别解密，得到的结果分别为（x1，x2，x3…x1001），解出来的1001 个数里面，只有一个恰好等于x。

接下来B 选取一个素数p，这个素数p应该比1001 略大，B 把解密得到的1001 个数全部模p，得到（s1，s2，s3…s1001）。 因为B 的工资是b，那么B 把后面（第b ＋1 项到第1001 项）全部加上一个随机数α，并乱序处理，然后与素数p打包后用A 的公钥加密传给A。

A 只需要验证x模p是否等于收到的数字序列中的某个数。 如果a ＞b，那么B 发送的序列中不存在模p与x同余的数，如果a ＜＝b，那么B 发送的序列中存在模p与x同余的数。 A 不可能知道b是多少，因为A 收到的序列是模p后的序列，A 不能把序列还原成模p前的序列，自然也就不能用B 的公钥返回去计算B 的工资。

这种方案相对比之下更加安全，但是对用户的计算需求较高。

4 工资中位数问题的改进方案

4.1 辅助运算方法

本节讨论的工资中位数问题的改进方案用到了两种辅助运算方法，一种是秘密比较的运算方法，另一种是利用最小堆求无序数组中位数的运算方法。

（1）最小堆排列计算求中位数

将前（n ＋1）／2 个元素调整为一个最小堆，对后续的每一个元素，和堆顶比较，如果小于等于堆顶，就将其丢弃，如果大于堆顶，就用该元素替换堆顶，并继续将堆调整为最小堆。 重复此过程，遍历全部元素，最终的堆顶就是中位数［11］。

1）假设Alice 的工资为1000，Bob 的工资为1800，Carol 的工资为1200，Dave 的工资为1100，张三的工资为1900，先建立完全二叉树，将前三个人的工资依次填入。

2）填入后，从Dave 开始与堆顶进行比较。

3）开始调整。 根据性质，小的数字往上移动。

4）最小堆建立完成后，让后2 位数字分别与堆顶数字进行比较如果小于等于，就跳过，接着看下一个数字。 如果大于，则用该数字取代堆顶数字，再将堆调整至最小堆，接着看下一个数字。 重复这个步骤，直到将后2 位数字全部遍历一遍。 遍历完成后的堆顶数字即为中位数。 最小堆排列计算流程如图1 所示。

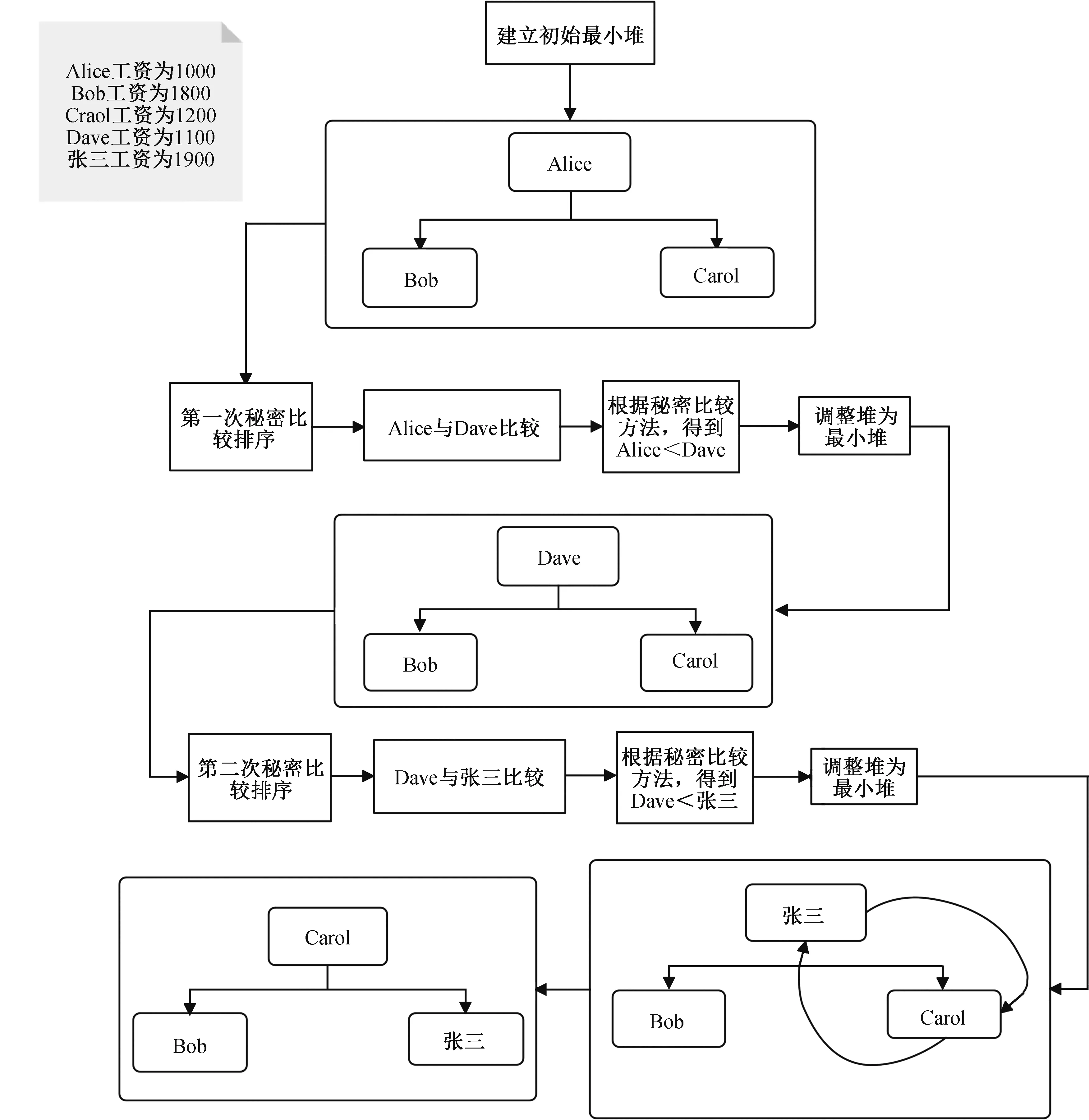
图1 最小堆排列计算流程解释

（2）秘密比较协议

当存在双方都想在不泄露自身工资信息的情况下比较两人的工资大小，那么此时就必须有一个秘密比较协议可以满足要求。 即在保证工资信息不会泄露的情况下比较工资大小［4］。

1）假设有两个人A、B，他们的工资分别是a、b（假设工资区间为1000 ～2000，且两人都可以使用计算机辅助计算）， 协议开始前，B 生成一对RSA 密钥。 首先，A 选取一个大随机数x，A 用B 的公开钥匙给随机数x加密，得到密文m。 A 把m减a的值发给B，那么B 实际接收到的数就是m-a。 接下来，B 尝试用私人密钥来恢复x。 由于B 不知道a是多少，于是B 枚举所有1000 到2000 之间的整数，用私钥对1000 ～2000这1001 个数分别解密，得到的结果分别为（x1，x2，x3…x1001），解出来的1001 个数里面，只有一个恰好等于x。

2）接下来B 选取一个素数p，这个素数p应该比1001 大，B 把解密得到的1001 个数全部模p，得到（s1，s2，s3…s1001）因为B 的工资是b，那么B 把后面（第b ＋1 项到第1001 项）全部加上随机数α，然后与素数p打包后用A 的公钥加密传给A。

3）A 只需要计算x模p是否等于序列中的某个数。 如果a ＞b，那么B 发送的序列中不存在模p与x同余的数，如果a ＜＝b，那么B 发送的序列中存在模p与x同余的数。 A 不可能知道b是多少，因为A 收到的序列是模p后的序列，A不能把序列还原成模p前的序列，自然也就不能用B 的公钥返回去计算B 的工资。 秘密比较协议流程如图2 所示。

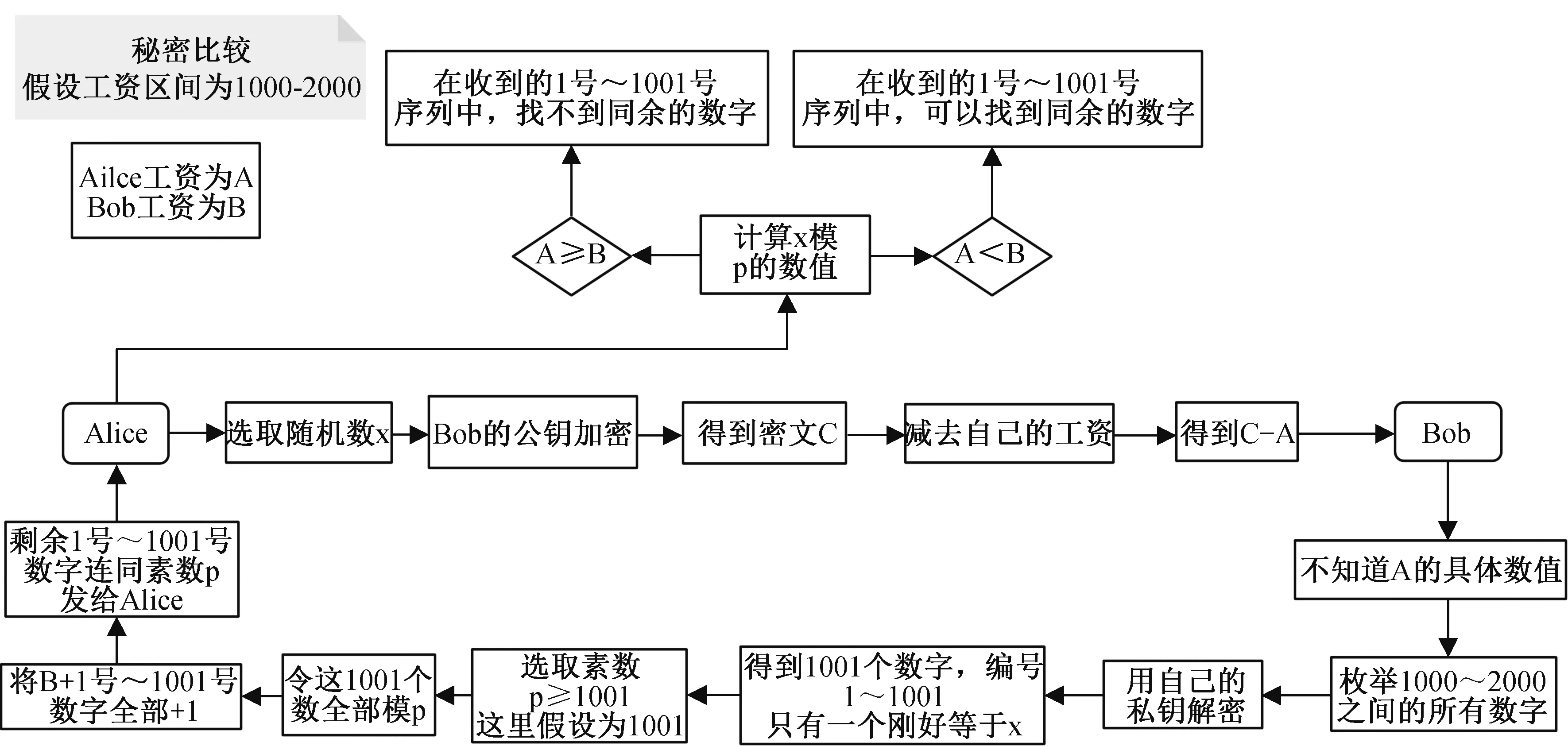
图2 秘密比较协议流程解释

4.2 具体方案

根据上文的计算方法，在进行深入思考与讨论之后，得出了一种结合了方案一计算中位数的优点，在完全去中心化的同时避免了信息泄露。下面本文将给出改进后的安全多方计算中工资中位数问题新设计，具体方案步骤如下：

（1） 假设有n个人， 分别是（N1，N2，N3…Nn），工资分别为（A1，A2，A3…An）。 这n个人序号分别为（1，2，3…n）。 那么情况一：n为偶数，让序号为1 ～n／2 的人按照顺序建立完全二叉树。 情况二：n为奇数，让序号为1 ～（n＋1）／2 的人按照顺序建立完全二叉树。 其余与情况一相同。

（2）序号1 生成RSA 密钥，公钥为root1，序号2 生成RSA 密钥公钥为left1， 序号3 生成RSA 密钥公钥为right1， 序号2 生成RSA 密钥公钥为root2， 序号3 生成RSA 密钥公钥为root3，序号4 生成RSA 密钥公钥为left2，序号5生成RSA 密钥公钥为right2， 序号6 生成RSA密钥公钥为left3……以此类推直到建立完全二叉树。

图3 方案前期流程图

（3）随后开始最小堆的建立，从序号1 开始进行秘密比较协议，序号1 与序号2 进行工资秘密比较，然后再与序号3 进行工资秘密比较，比较完成后，按照最小堆的规则进行序号交换。 由于秘密协议只在这3 个人中进行，所以工资信息不会外泄，同样序号交换的结果也不会外泄。 然后再从序号2 开始进行秘密比较协议，序号2，序号4，序号5 之间进行两两工资秘密比较，根据最小堆的规则进行序号交换。 以此类推直到完成最小堆的建立。

（4）随后遍历序号n／2＋1 ～n（奇数则为（n ＋1）／2＋1 ～n）分别与堆顶序号进行工资秘密比较，如果小于等于堆顶序号，则跳过，如果大于，则该序号与堆顶序号进行交换。 随后重复2过程，直到序号n／2 ～n都被遍历，此时堆顶序号的工资就是工资中位数。 且只有堆顶序号知道自己的工资是中位数。 每个人重新生成一个临时的私钥与公钥。 所有人将自己的工资随机分为n－1 份，（工资处在中位数位置的人可以撒谎将工资乘以2 后再随机分为n－1 份）分别用Nj（j＝1， 2， 3…n）（除自己以外）的公钥加密，用自己的私钥即签名，发给Nj（j ＝1， 2，3…n）。

图4 方案中间流程图

（5）所有人完成分发后，N1将自己收到的n－1 个数据加和，减去自己的工资后。 将得到的结果发给下一个人，下一个人收到数据后，将数据与自己之前收到的n－1 个数据加和，减去自己的工资，将得到的结果发给下一个人。 重复直到所有人都将自己的工资减去，最后一个人得出工资中位数。

4.3 改进方案分析

本小节将对工资中位数问题的改进方案进行分析，改进方案与原始方案相比有许多优势，并且方案的安全性和可行性都得到了增强，因此本小节将主要从改进方案的优势以及方案的安全性这两个方面进行分析。

（1）改进优势分析

改进思路的目的是在具有隐私性、计算正确性及去中心化的特性的同时具有简单的原理和较强的可行性。 方案一实际上并没有满足安全多方计算中的安全要求，并且存在信息泄露隐患，参与信息秘密比较的两个人都会知道对方的工资。 在信息秘密比较环节存在工资隐私数据泄露问题，但是方案一中的对工资信息进行公私钥加密的设计思路以及中位数计算的思路可以借鉴。

与方案一进行对比，改进方案采取的加密措施是在加密时使用非对称密码算法，甲选取一个随机数用乙的公钥进行加密，随后将加密的结果减去自己的工资然后再发给乙，乙会用自己的私钥进行解密，但是解密的结果并不是甲选的随机数，于是乙就会枚举工资区间，并对所有数进行解密。 随后乙会再选一个随机数m， 然后让所有数都模m， 随后将结果发给甲，甲会进行对比，从而得出两人工资比较的结果。

这里相当于信息在公开信道中进行加密传输以及信息在密态下的秘密比较，在双方隐私没有被泄露的同时，将信息传递给对方，然后对双方的工资信息进行比较，再通过最小堆排列计算求中位数的方式，进行对工资中位数的计算。

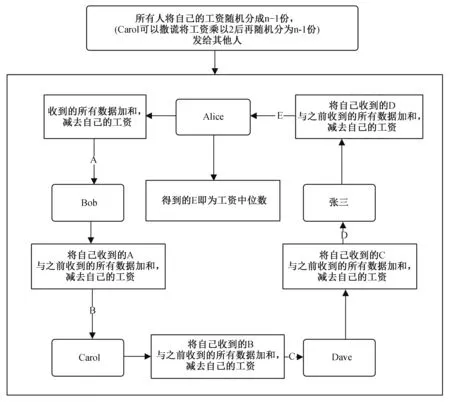
图5 方案后期流程图

（2）方案安全性分析

由于方案一存在的问题是安全性得不到保障，两名用户在进行工资数据信息比较时，会先将工资数据进行拆分，然后再进行加密后发给其他人。 在此处对工资数据进行的加密虽然会保证信息在被截取的情况下，截获者也不能解密得出拆分后的结果。 但是在其他人对收到的两份数据进行大小比较后，将结果再加密然后发回两名用户后，两名用户会对收到的信息进行比较，信息比较完成时，两名用户会对收到的所有返回数据进行加和得出双方的工资差值，于是两名用户就会得知对方的工资数据信息。

接下来将进行证明改进后的方案比方案一更加安全，在这里我们先假设在只有五个人的情况下进行比较。M1，M2，M3，M4，M5工资分别为1000，1800，1200，1100，1900。 首先用方案一的计算方法进行计算，M1与M2先进行第一轮比较，将自己的工资随机分为n－2 份，即3 份，并分别分发给M3，M4，M5。 下面M3，M4，M5将比较后得到的数据发给M1，M2那么M1得到的数据为－800，M2得到的数据为800，这表示M1的工资比M2小800，那么M1就可以根据这个数值和自己的工资数得到M2的工资，同理M2也可以根据收到的数据得出M1的工资。 这就存在安全风险，进行工资比较的双方工资信息遭到了泄露。

下面我们再使用改进后的方案进行计算，首先让M1，M2，M3的工资数据生成最小堆，具体方法在上文中已经描述，这里就不多赘述。 其中在进行工资比较时使用的方法是上文中的秘密比较协议［4］主要运用的计算方法有数字取余和RSA 算法加密。 而且在进行工资比较时，是对加密后的数据进行比较，在私钥没有泄露的情况下，工资信息是不会泄露的。 所以安全性相较于方案一可以得到有效的保障。

改进方案的流程设计沿袭方案一的“中位数计算”与“公私钥加密”的方法，达到更加安全可靠的效果，将方案流程上的风险进一步降低，增加其安全性。 与方案一进行对比，改进方案保证了完全的去中心化，并且利用数字取余，增强了安全性，保证了数据的安全可靠，同时因为频繁对工资数据进行公私钥加密，减小了数据在传输过程中发生信息泄露的可能性。 同时改进方案设计原理较为简单，只是操作流程稍微复杂，而且极大地增强了可行性与安全性，但是由于方案中存在枚举过程与取余过程，所以计算量较大。

5 总结

随着现代密码学的不断发展，安全多方计算理论在信息安全领域以及密码保密领域起到了越来越大的作用。 随着人们对个人隐私和信息安全的关注度逐渐提高，对于安全多方计算的安全性、隐私性和去中心化程度的要求会越来越高。 本文所探讨的工资中位数问题就是在这种大环境下的产物。 工资中位数又称收入中位数，是指用统计学上中位数的概念来衡量某地区普通民众的收入水平，相比较于人均收入，收入中位数更贴近普通民众的实际生活水平，因为某地区的人均收入因贫富的差距可远远大于收入中位数，而收入中位数则可以将这种差距反映出来。 中位数算出来可避免极端数据，代表着数据总体的中等情况。 例如，一个公司内部可能基层与高层之间收入差距较大，这时如果要衡量公司内部的收入水平，就不能单纯的采取计算工资平均数的方式。

本文对已有的安全多方计算中工资中位数问题的问题解决思路进行了分析，发现其隐藏的安全隐患，取长补短设计出原始方案虽然解决了工资中位数问题，但是其安全性并没有得到保障。 于是在已有问题解决思路以及原始思路的基础上，对现有的安全多方计算中工资中位数问题的原始解决方案进行了深入解读分析，发现其隐藏的安全隐患，取长补短设计新方案，解决了原有的工资隐私信息数据泄露问题，其创新点主要有，利用数字取余进行密态数字比较，利用最小堆的特性进行中位数的计算。 同时新方案设计原理简单，可行性高，适用于工资中位数或者其他中位数计算。

但是不可否认，本文提出的改进方案依旧有着缺陷，因为该方案建立在半诚实模型基础上，所以无法保证在有攻击者或参与者撒谎的情况下得出正确的工资中位数结果，因此在下一步的计划中将对于这个缺陷进行进一步的研究，并争取将其解决。