一种改进的多领导鲸鱼优化算法

余贤星

(上海理工大学机械工程学院，上海 200093)

yvxianxing@163.com

1 引言(Introduction)

鲸鱼优化算法的优越性有目共睹，因此该算法在优化问题上应用广泛。但其存在收敛速度慢、收敛精度低、搜索能力不足的缺点，各种改进的鲸鱼算法应运而生。其中改进方式有将两种算法的优势结合而成，也有通过其他策略。ZHANG等提出了一种基于聚集策略的混合鲸鱼优化算法，将鲸鱼优化算法和灰狼优化算法优势结合。林杰等提出了一种基于混沌的正余弦鲸鱼优化算法，加快了算法的收敛速度，避免了早熟，平衡了搜索与开发。郭启程等提出了一种基于莱维飞行的鲸鱼优化算法，用于解决无人机三维路径规划问题。董明明等为了解决现有辊道窑窑温异常检测存在的各种问题，提出了一种采用自适应反向学习策略和高斯变异算子的改进鲸鱼优化算法。刘紫娟等提出了一种改进的离散鲸鱼优化算法，用于应对复杂网络社区发现的应用场景。朱诚提出了一种引用双非线性收敛因子和强制驱散机制改进的鲸鱼优化算法，能够有效简化路径复杂度、降低机器人控制难度。

本文提出了一种改进的多领导鲸鱼优化算法，该算法引入了多领导机制和莱维飞行机制。多领导机制是将初始种群均分为四个小种群，每个种群根据各自种群的最优位置进行迭代更新。每10 次迭代进行一次种群重组，有利于提高种群的多样性，避免整个搜索过程陷入局部最优。莱维飞行机制是将每代的最优位置进行随机扰动，有利于加快收敛，避免陷入局部最优。通过标准方程和现实生活问题进行验证，表明了该算法的优越性。

2 鲸鱼优化算法(Whale optimization algorithm)

2.1 围捕猎物

座头鲸能够感知猎物的位置并发动攻击。在一个最优位置不确定的搜索空间里，假设所有座头鲸的最佳位置就是最优或者在最优位置旁边。那么一旦确定最优的座头鲸位置，其他鲸鱼就会根据最优更新。更新公式如下：

2.2 泡泡网攻击方式

座头鲸沿着曲率半径越来越小的螺旋线路径向上游动，通过吐泡泡的方式，形成一堵气墙，将猎物围在一起最后捕杀。泡泡网攻击模型中包含两种方式：一种是收缩环绕，通过递减的值，影响的范围；另一种是螺旋更新，位置更新公式如下：

由于两种更新方式同时发生，因此添加一个概率数，来决定具体使用哪一种更新方式。

2.3 搜寻猎物

收缩环绕更新中，目标鲸鱼可能是最优位置鲸鱼，这就是进行开发阶段；也可能是其他任意鲸鱼，这就是搜索阶段。当进行到搜索阶段时，鲸鱼位置更新公式如下：

2.4 鲸鱼算法的更新方式总结

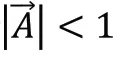
3 改进的鲸鱼算法(Improved whale optimization algorithm)

3.1 多领导机制

该算法中引入多领导机制是为了提高种群的多样性，避免搜索个体陷入局部最优。如图1所示，初始化一个种群，将其均分为4 个小种群，每个种群对应各自的最优个体位置，每次迭代都根据各自种群的最优位置进行更新。每10 次迭代结束，就会进行一次种群间的信息交流，就是将各种群内的个体进行一次打乱重组，有利于扩大搜索范围，避免陷入局部最优。

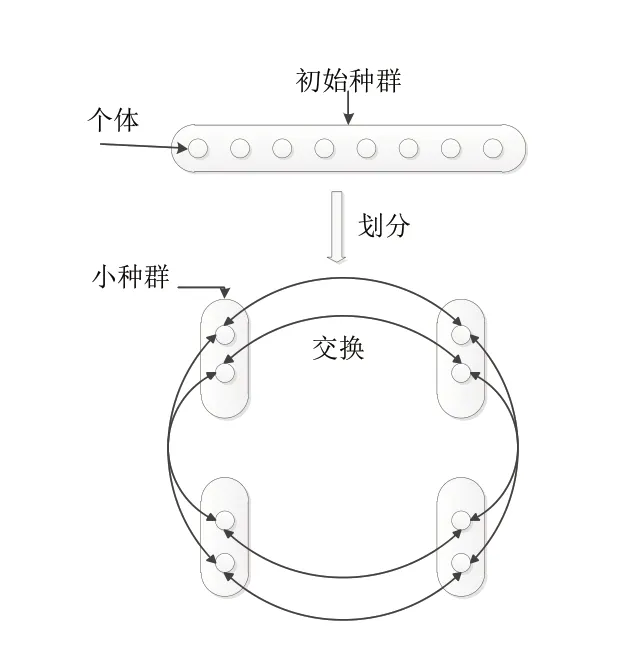
图1 多种群机制Fig.1 Multi-population mechanism

3.2 莱维飞行机制

该算法引入了莱维飞行机制，为了将最优位置进行随机扰动，加快收敛速度，避免陷入局部最优。更新公式如下：

其中，Γ 是Gamma函数。

3.3 算法流程

算法IWOA伪代码如下所示。

4 标准方程测试(Benchmark functions test)

4.1 试验设置

CEC2014标准函数是测试算法性能的重要实例。从中选取6 个标准函数，详见表1，其中、、是单峰函数，、、是多峰函数。单峰函数只有一个全局最优解而没有局部最优解，用来测试算法的开发性能，得到的最优解精度越高，表明算法具有更优的开发性能。多峰函数只有一个全局最优解却含有多个局部最优解，而且随着函数维度升高，优化复杂度越高，用来测试算法的搜索能力和开发能力。对于搜索能力不足的算法，在优化多峰函数时容易陷入局部最优。将该算法与其他先进的算法比较，其中包括粒子群算法(PSO)、灰狼优化算法(GWO)、鲸鱼优化算法(WOA)、混合鲸鱼灰狼优化算法(HWOAG)、提升的鲸鱼优化算法(WOAmM)。对于这些算法中的参数设置，详见表2。

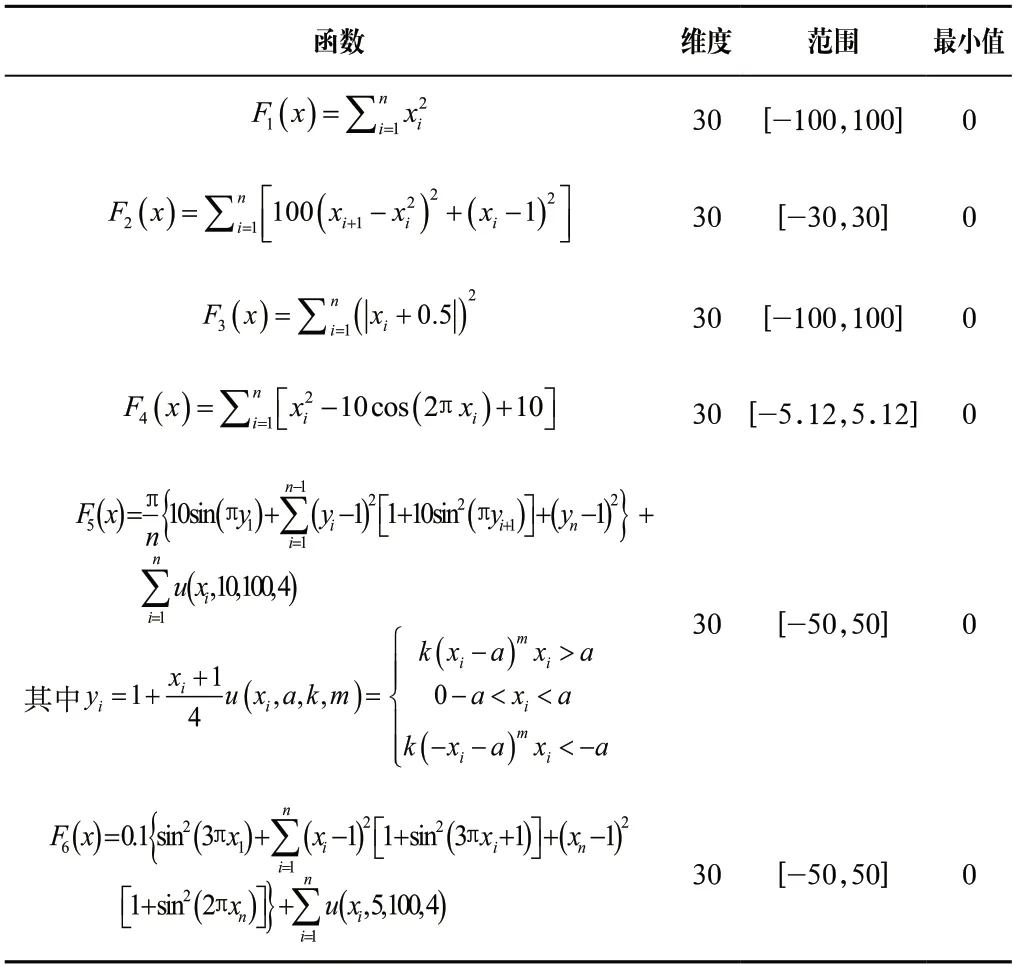
表1 6 个标准函数Tab.1 Six benchmark functions

表2 算法参数Tab.2 Algorithms parameters

4.2 测试结果

将所有的算法在32 个个体、500 次迭代次数、30 次运行次数的情况下，对30 维的标准函数进行测试，统计最优解的平均值和标准方差。平均值能够直观展示算法的效果，而标准方差能够判断算法的稳定性。优化结果对比详见表3。

表3 6 个函数的对比结果(32 个个体，30 维)Tab.3 Comparison results of 6 benchmark functions(N=32，D=30)

从统计数据可以看出，在6 个测试函数中，相比于其他5个算法，该算法的优化结果最小。从平均值可以看出，该算法相比于其他几个算法，收敛精度更高，而且在上取得了最小值0。从标准方差可以看出，该算法具有高稳定性。

4.3 收敛分析

收敛性是算法的一个重要衡量标准，收敛速度越快，算法效率越高。如图2所示，对于单峰函数，所有算法都能快速收敛，相比于其他几个算法，该算法具有很强的后期开发能力，最优解的精度高。对于多峰函数，该算法在迭代前期收敛比较慢，大部分个体用于搜索，接着就会有一个加速收敛的过程，算法对可能性大的区域进行搜索，这时候算法已经确定了最优解的大概位置，因此搜索个体会在最优位置周围进行开发，最后收敛曲线放缓。而其他算法刚开始就快速收敛，当进行到搜索中后期的时候，最优解一直不变，停滞不前，此时算法已经陷入局部最优。其他算法开发能力不强，即使找到可能性大的区域，得到的最优解精度也不够。如图3所示，箱线图也表明了算法的求解精度高而且稳定。

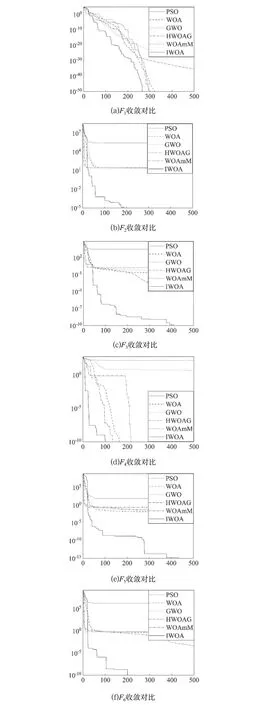
图2 不同函数收敛曲线图Fig.2 Convergence line graphs of different functions

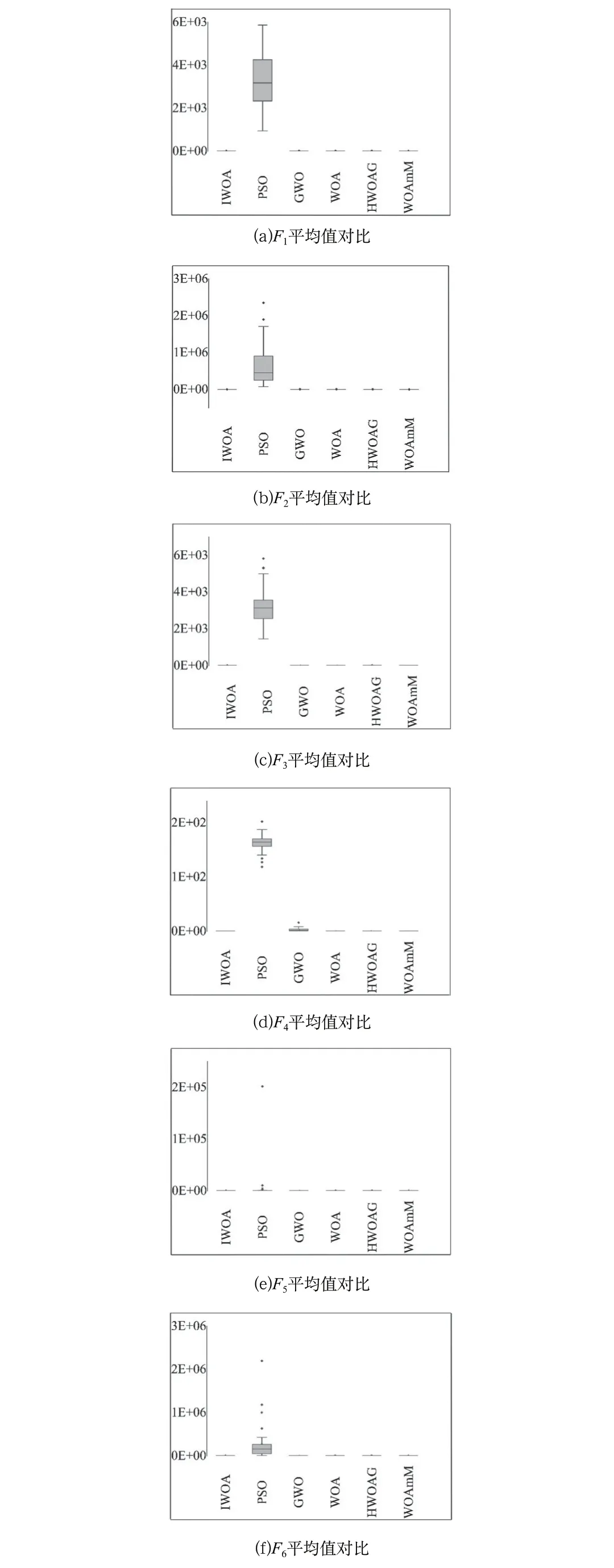
图3 不同函数箱线图Fig.3 Boxplots of different functions

5 工程优化问题测试(Engineering optimization problems test)

现实生活中有许多经典的多变量工程问题，被许多学者作为优化算法的测试实例。本文选取了三个约束问题，通过改进的多领导鲸鱼优化算法进行优化，并与其他算法进行比较，其中部分优化结果来源于提升的鲸鱼优化算法。以下是这三个问题的描述。

5.1 悬臂梁的设计问题

悬臂梁由五个等厚的空心方块组成。梁在第一块上有刚性支撑，在第五块的自由端有一个垂直力作用。悬臂梁结构示意图如图4所示。这个问题需要最小化悬臂梁的重量，并且满足开口端垂直位移上限的约束要求。、、、、(mm)分别表示五个空心方块的长度。目标方程、约束条件和变量范围如下。

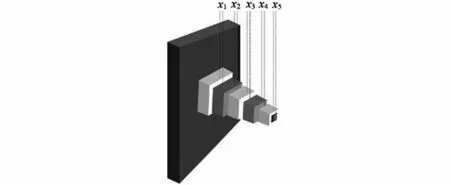
图4 悬臂梁结构示意图Fig.4 Cantilever beam structure figure

目标函数：

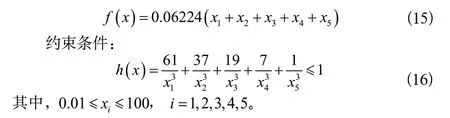
从表4中可以得出，在悬臂梁的设计问题中，该算法得到了最小值1.3365。相比于其他算法，值都略优。从结果可以看出，该算法的求解精度高，在最优值周围区域，开发精度很高。虽然其他算法也得到了近似值，但由于其他算法精度不高，因此略显劣势。

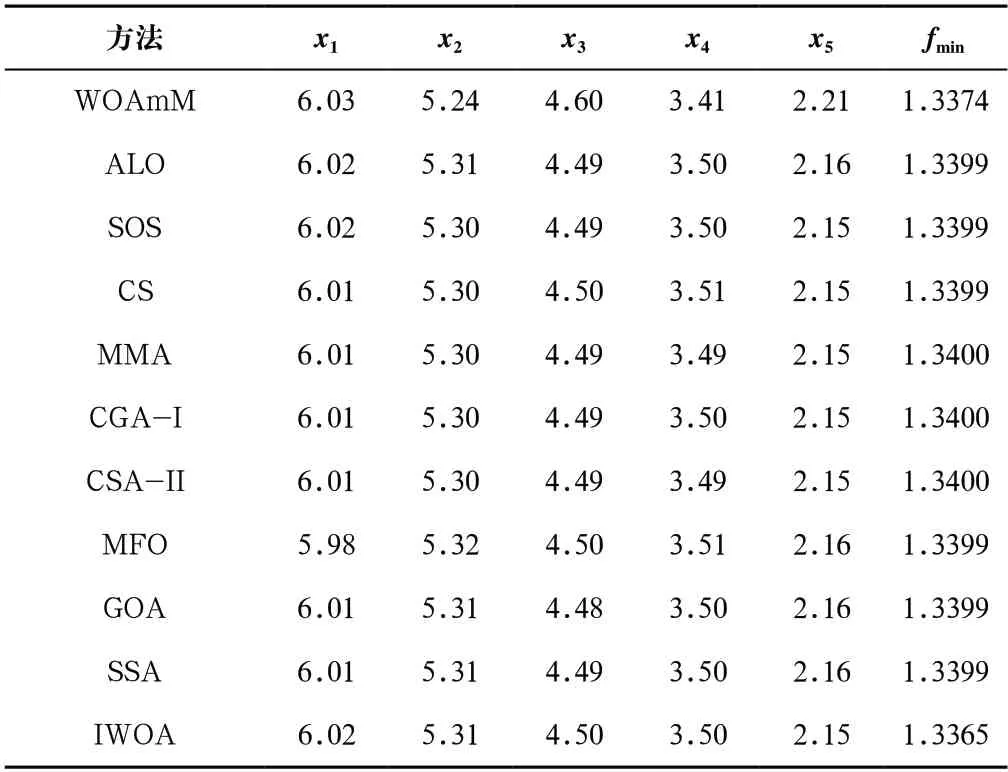
表4 悬臂梁设计问题的结果对比Tab.4 Comparison of results on cantilever beam design problem

5.2 三杆桁架设计问题

如图5所示的三杆结构和受力情况下，在满足弯曲、挠度、应力时最小化三杆桁架的体积，这个问题就是通过两个变量、(cm)调整横截面积。目标方程、约束条件和变量范围如下。

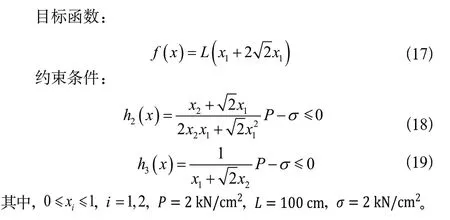
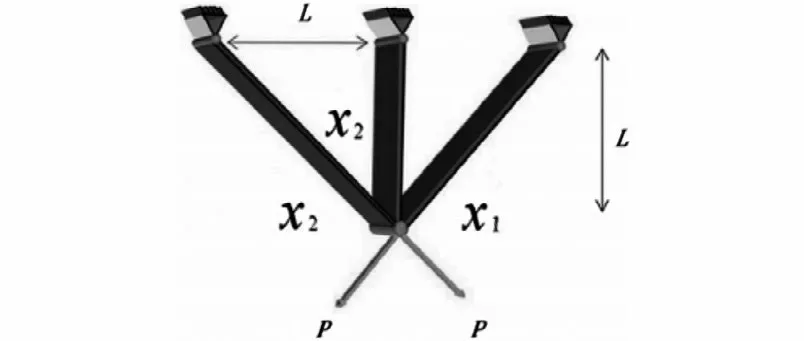
图5 三杆桁架结构和受力示意图Fig.5 Three-bar truss structure and force figure

从表5中可以看出，所有算法都得到了相同值，除了Ray&Sain，因此，在这个具有两个变量的问题中，所有算法都到了最优值。说明了该算法在提升搜索能力的同时，也具有很强的开发能力。

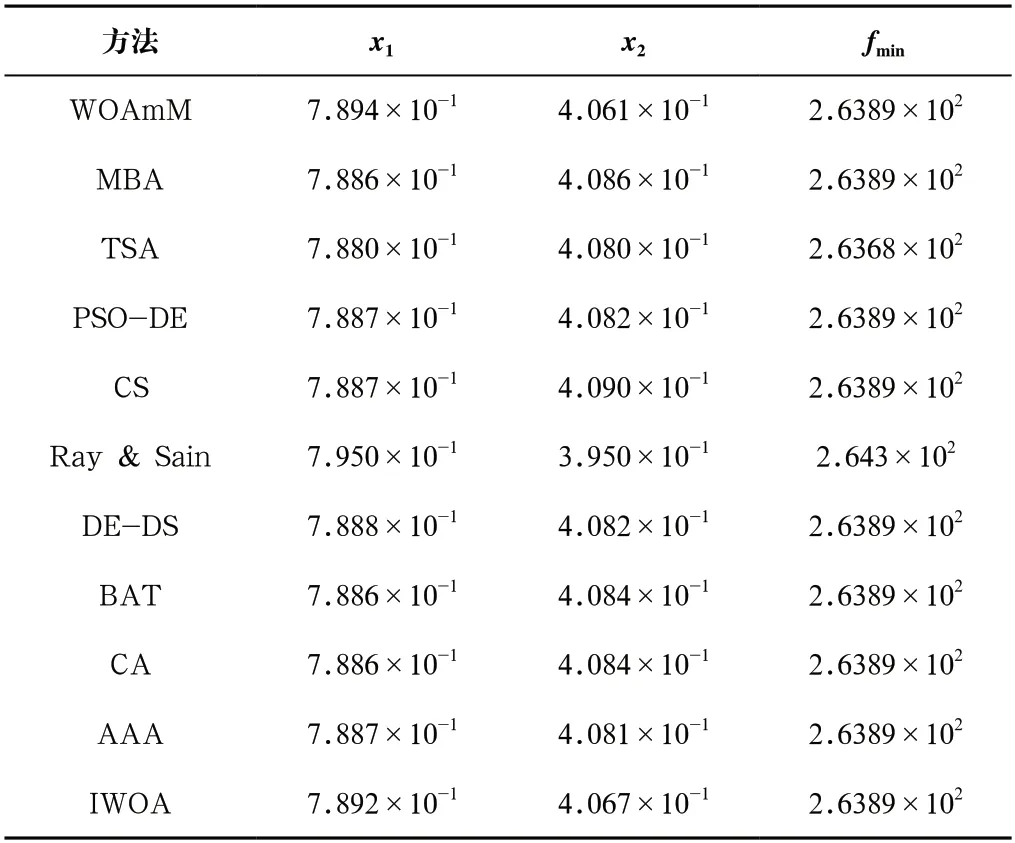
表5 三杆桁架设计问题的结果对比Tab.5 Comparison of results on the three-bar truss design problem

5.3 输气压缩机设计问题

这是一个具有四个变量的机械设计问题，目标是确定变量的值，以便使用最低成本能每天传输1亿立方米的天然气系统。其中一个变量是压缩机站的距离(m)，第二个是压缩机的效率，第三个是管道的直径(cm)，第四个是管道的速率(m/s)。目标方程、约束条件和变量范围如下。

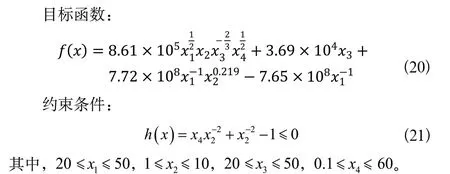
从表6中可以看出，该算法得到了最小值，且远优于其他算法。该算法在搜索能力上有很大的提升，能避免陷入局部最优，很大提升了算法的优越性。其他算法都得到了近似值，说明其他算法陷入了局部最优解。而改进的多领导算法，因为莱维飞行和多领导机制，直接使算法跳出局部最优，向更优区域进行搜索开发。

表6 输气压缩机设计问题的结果对比Tab.6 Comparison of results on gas transmission compressor design problem

6 结论(Conclusion)

本文提出了一种改进的多领导鲸鱼优化算法。该算法引入了多领导机制，有利于提高种群的多样性，防止陷入局部最优；引入莱维飞行机制，将最优个体进行随机扰动，加快收敛速度，防止陷入局部最优。通过6 个标准函数进行测试，从平均值和标准方差可以看出，该算法在收敛精度和稳定性上，相比于其他算法有很大优越性。从收敛图可以看出，该算法收敛速度快，收敛精度高。同样在箱线图中可以看出，该算法准确性高，无论是单峰函数还是多峰函数，都能准确判断最优位置区域，并在最优位置周围开发。通过三个工程优化实例进行验证，该算法都能得到最优值。后续可以将该算法运用到其他机械设计问题中。