光电系统伺服稳定平台可靠性定性分析

郑凤翥，宁 飞，王惠林，吴雄雄，王 冠，赵志草，周 云，王 乐

（西安应用光学研究所，陕西 西安 710065）

引言

光电系统是载机的重要任务设备之一，利用可见光摄像机、红外热像仪、激光测距机等关键光学传感器，可实现对特定区域、特定景物的远程、高清成像，而伺服稳定平台是光电系统的骨架、神经，其可靠性水平将严重影响光电系统的功能、性能。因此，对伺服稳定平台开展可靠性分析至关重要。故障模式、影响及危害性分析（FMECA）是一种有效的可靠性定性分析方法，它通过系统地分析，确定元器件、零部件、设备、软件在设计和制造过程中所有潜在的故障模式，以及每一个故障模式的原因和影响，并按故障影响的后果对每一个潜在故障模式划等分类，以便找出潜在的薄弱环节，提出改进措施[1]。然而，在利用FMECA 得到关键故障模式及可靠性关重产品后，在后续的可靠性设计、可靠性指标分配中，人为主观判断的影响较大。因此，为降低人为主观判断对设计、分配结果的影响，提高可靠性定性分析对可靠性设计、可靠性指标分配的指导作用，在得到可靠性关键故障模式及关重产品后，将继续深入分析关重产品对可靠性影响的重要度排序。

1 伺服稳定平台FMECA

伺服稳定平台，作为光电系统的结构支撑，为光电传感器、图像处理单元、减振装置等提供安装平台；同时，在任务计算机板、电源板、伺服接口板、伺服驱动板、电机、旋变、陀螺等组件的协调配合下，响应操控人员指令，驱动光电系统在方位向、俯仰向运动[2]。

机械结构件虽然采用无限寿命设计，但机械组件的装配精度、磨损等可影响伺服稳定平台可靠性，故本文将机械组件作为单独硬件单元，参与伺服稳定平台FMECA，并以此为依据，要求在后续可靠性分配中，对其分配相应的可靠性指标。

1.1 故障严酷度类别及发生概率

根据伺服稳定平台的每个故障模式对光电系统的最终影响程度，确定其严酷度类别。光电系统严酷度类别及定义如表1所示。

表1 光电系统严酷度类别及定义Table 1 Severity category and definition of electro-optical system

危害度等级严格按照GJB/Z 1391—2006 《故障模式、影响及危害性分析指南》，定性危害性矩阵分析时，将每个故障模式发生概率的等级划分为A、B、C、D、E 五级。

1.2 可靠性关重产品

通过对伺服稳定平台硬件故障模式、影响及危害性分析，伺服稳定平台共24 个故障模式中，没有严酷度为Ⅰ类的故障，严酷度为Ⅱ类的有17个。得到伺服稳定平台可靠性关重件清单如表2所示。

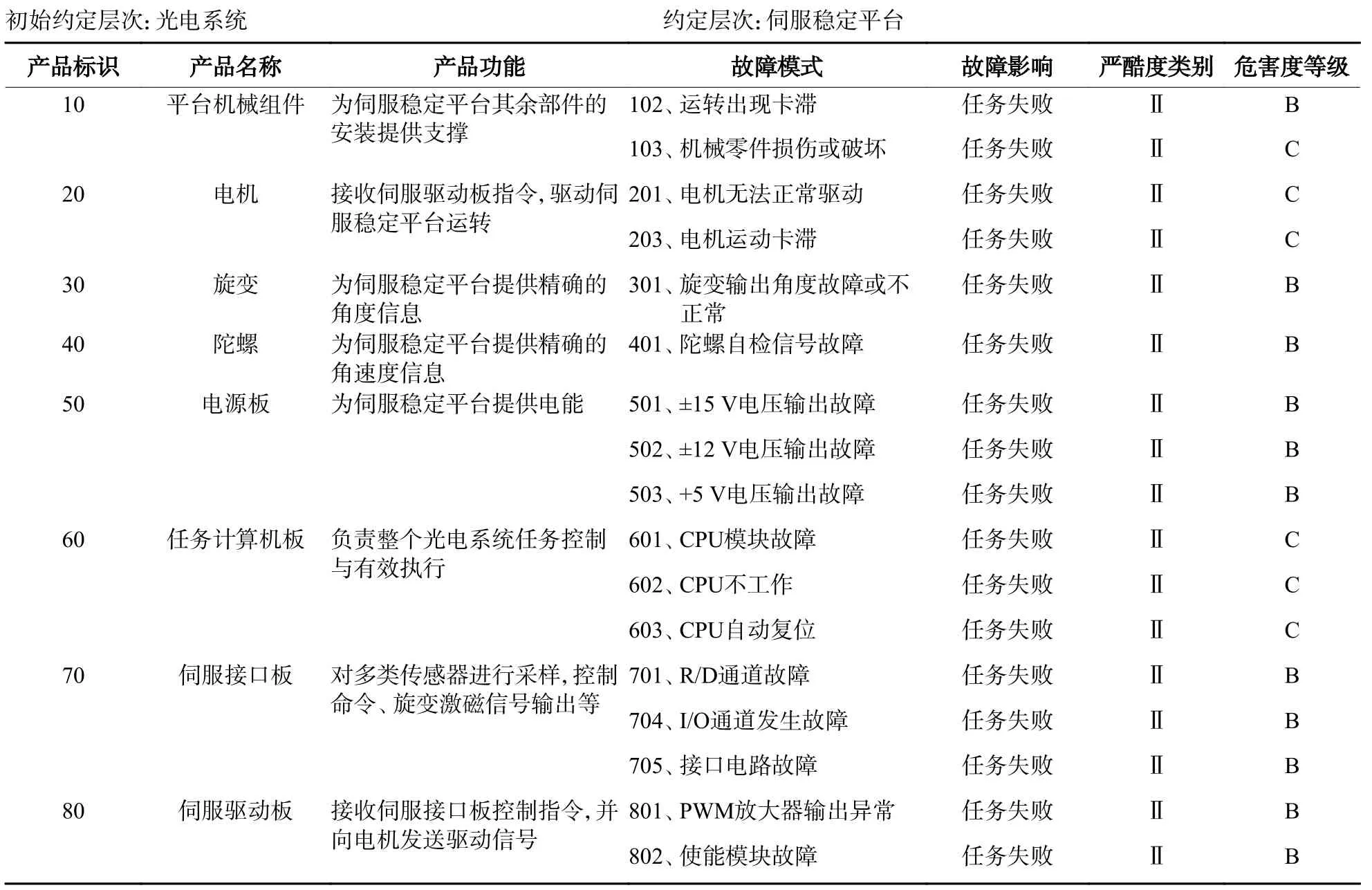
表2 可靠性关重产品清单Table 2 List of reliability critical products

从表2 可知：平台机械组件10、电机20、旋变30、陀螺40、电源板50、任务计算机板60、伺服接口板70、伺服驱动板80 为伺服稳定平台可靠性关重产品，对关重产品对应的关键故障模式应通过设计改进、使用补偿等措施予以消除。

2 可靠性关重产品重要度分析

虽然，借助FMECA 得到了伺服稳定平台的可靠性关重产品，但受限于技术水平、体积质量、成本控制等，无法对关重产品的每个关键故障模式采用设计改进、使用补偿等措施一一消除。因此，需对关重产品的重要度进行深入分析，将重要度高的关重产品对应的关键故障模式采用设计改进、使用补偿等措施予以消除，对无法通过该措施予以消除的关键故障模式，其对应的关重产品在后续可靠性分配时应分配较高的可靠性指标，以提高伺服稳定平台可靠性。

2.1 模糊层次分析法

模糊层次分析法是基于模糊一致关系和模糊一致矩阵的模糊集合理论，它是在层次分析法的基础上，充分考虑了人为主观判断的模糊性，是一种更好地处理含有模糊性的决策问题的分析方法。该方法的分析思路是：将复杂分析对象分解为目标层、准则层和指标层，对同一层的指标，两两之间的重要程度做出判断，建立判断矩阵，并计算出每一因素对高一层指标重要性程度的权重，得到判断矩阵对应的权重向量，为最优选择提供依据。它能利用较少的定量信息使决策的思维过程数学化，进而为多目标、多准则和无结构特性的复杂决策问题提供基于数学理论的分析方法[3-13]。

2.2 重要度分析

1）建立多级递阶结构

目标层A 为伺服稳定平台可靠性，准则层B 为快速性（响应的快速性）、精准性（控制的精准性）、平稳性（运动的平稳性），方案层C 为平台机械组件、电机、旋变、陀螺、电源板、任务计算机板、伺服接口板、伺服驱动板。建立的多级递阶结构如图1所示。

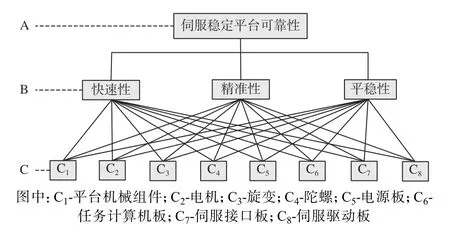
图1 伺服稳定平台多级递阶结构Fig.1 Multilevel hierarchical structure of servo stabilization platform

2）建立模糊互补判断矩阵

根据已建立的伺服稳定平台多级递阶结构，采用0.1～0.9 标度法，对2 个因素的相对重要程度做出定量表示，得到各级互补判断矩阵如下：

式中：PA为3 个判断准则对伺服稳定平台可靠性影响重要程度的互补判断矩阵，即A级判断矩阵；PBi(i=1,2,3)分别为各方案单元从快速性、精准性和平稳性3 个判断准则对伺服稳定平台可靠性影响重要程度的互补判断矩阵，即B级判断矩阵。

3）判断矩阵权重向量计算

权重向量的计算采用文献[14]中的公式：

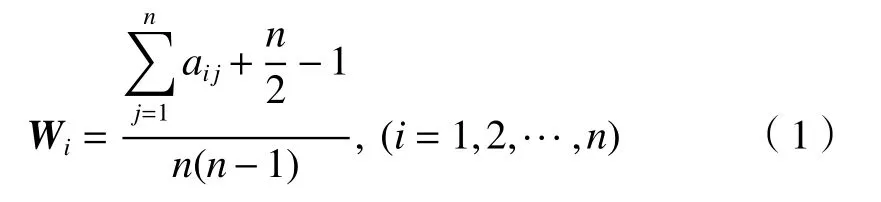
利用该公式计算以上互补判断矩阵对应的权重向量如下：

3 个判断准则对伺服稳定平台可靠性影响的权重向量为

WA=(0.333 3,0.383 3,0.283 3)T

各判断准则下8 个方案单元的权重向量为

4）判断矩阵对应的特征矩阵计算

各判断矩阵对应的特征矩阵按如下公式计算：

式中：W=(W1,W2,···,Wn)T是判断矩阵的权重向量；计算得到各特征矩阵如下：

5）判断矩阵的一致性检验

一致性检验是检验判断矩阵建立是否合理的依据，可用判断矩阵的相容性来检验一致性。矩阵A=(ai j)n×n和矩阵B=(bij)n×n的相容性指标采用文献[15]中的公式计算。

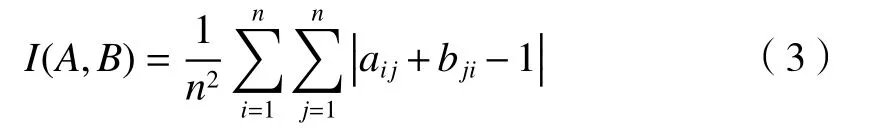
当相容性指标I(A,B)≤α时，认为判断矩阵为满意一致的。 α越小表明决策者对模糊判断矩阵的一致性要求越高，一般取 α=0.1。

利用上述公式，计算各判断矩阵与其相对应的特征矩阵的相容性指标如下：

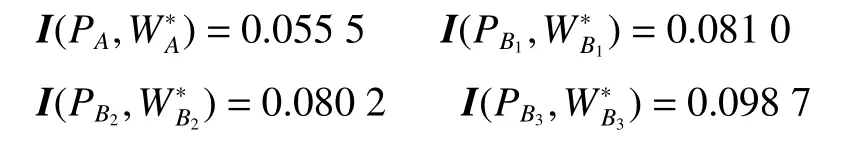
由计算可知：每个判断矩阵与其对应的特征矩阵的相容性指标均小于0.1，认为每个模糊互补判断矩阵是满意一致的，其权重集的分配是合理的。

因此，有排序向量组成的评判矩阵R为

式中：B1为 快速性；B2为 精准性；B3为平稳性。

6）各方案单元对伺服稳定平台可靠性影响重要度的总排序

总排序结果计算如下：

式中的算子“ O”采用模糊数学的加权平均型运算法则（见公式4），它可以兼顾到各方案单元对伺服稳定平台可靠性的影响，更能体现对伺服稳定平台可靠性研究时的全局观。

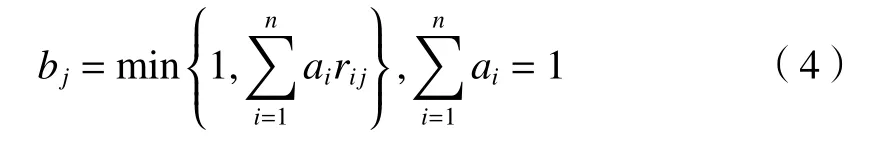
由（4）式得出各方案单元对伺服稳定平台可靠性影响的重要度见表3。

表3 各方案单元对伺服稳定平台可靠性影响的重要度Table 3 Importance of influence of each scheme unit on reliability of servo stabilization platform

结合模糊理论中的最大隶属度原则，确立的各方案单元对伺服稳定平台可靠性影响重要度的排序为：C2＞C1＞C8＞C3＞C5＞C7＞C4＞C6，对 应 的方案单元为：电机＞平台机械组件＞伺服驱动板＞旋变＞电源板＞伺服接口板＞陀螺＞任务计算机板。

3 结论

本文将传统的FMECA 和模糊层次分析法相结合，提出了一种可有效降低人为主观判断对可靠性设计、分配影响的解决思路。在此基础上，以光电系统伺服稳定平台为研究对象，深入分析了关重产品对伺服稳定平台可靠性影响的重要度排序，该重要度排序将作为后续可靠性设计、可靠性分配的重要依据和参考。因此，可将重要度对可靠性设计与分配的指导研究作为后续研究的方向。