考虑取送交叉和多种扰动因素的外卖配送路径优化研究

熊浩，郭昊颖†，鄢慧丽，陈锦怡

（1.海南大学管理学院，海南海口 570228；2.海南大学旅游学院，海南海口 570228）

近年来中国在线外卖市场规模占餐饮行业市场规模的比例逐年攀升，新冠肺炎疫情改变了人们的就餐习惯，外卖已成为疫情环境下中国餐饮业新的增长点.截至2021 年12 月末，中国网上外卖用户规模达5.44 亿人，较2020 年同期增加了1.25 亿人，同比增长29.83%.

随着外卖行业的不断发展，许多问题也逐渐显现，例如在上海、重庆、烟台等十几个城市均发生过多起骑手集体抗议以反映外卖配送中存在的相关问题，主要包括指派的订单距离远、没有考虑骑手电动车续航能力、拒单的惩罚过于严格等.这是因为平台在构建外卖配送路径优化模型和算法时，大多只考虑平台利润和顾客满意度等方面，而未充分将骑手的目标考虑在内，从而未能较好地平衡平台、顾客、商家和骑手之间的利益.

现有关于外卖配送路径优化问题的研究中，众多学者借鉴了带时间窗的取送货问题［1-4］，并取得了一定的研究成果.在模型构建方面，现有研究的优化目标主要集中于客户时间满意度［5］、时间惩罚成本［6］、顾客满意度和配送成本［7］、商家和顾客满意度［8］、总收益［9］、顾客期望时间窗和时间惩罚成本［10］、配送系统服务速度、配送员个人总收益和顾客等待时长［11］以及总配送距离［12］等方面.可见，现有外卖配送路径优化模型的目标函数中，对于骑手到达商家节点的空驶距离成本，以及骑手在商家节点或顾客节点的时间等待成本等目标考虑较为欠缺.这也将导致骑手利益受损，甚至“被困在系统里”.

在算法选择方面，该问题同属NP-hard 问题.由于外卖配送对算法时效性要求极高，启发式算法或元启发式算法因其求解速度快、求解效率高成为求解该问题的主要算法，部分学者也将启发式算法与运筹优化、机器学习和深度强化学习等方法结合，对外卖配送路径优化问题进行求解.

另外，骑手在配送过程中可能面临众多的扰动因素.外卖配送中的扰动因素是指骑手在配送过程中遇到的突发状况，导致骑手无法在算法原有规划路径或原有计算时间内将餐品送达.较为常见的扰动因素有骑手中途接单、临时交通管理、商家出餐时间异常和顾客取餐时间异常等.当扰动因素出现时，只需要针对个别订单进行改派和转单，不需要大规模的重新优化［13］.

尽管考虑扰动因素的外卖配送路径优化研究较为欠缺，但现有关于扰动管理在车辆路径中的研究为骑手扰动管理下的路径优化提供了重要参考.例如王旭坪等［14］针对带回程取货车辆路径问题中出现的需求变化扰动，提出了带回程取货车辆调度的扰动恢复模型，并设计了基于邻近策略和增派策略的启发式算法对模型进行求解.王征等［15-16］针对行驶时间延迟下配送车辆调度的扰动管理问题，以顾客时间窗偏离程度最小化和配送成本最小化为目标，建立了问题的数学模型及其求解算法.沈哲［17］等对因实际流场与空风洞之间区别产生的偏差进行分析，分别对车辆所在自由空间、空风洞与带实际车辆的风洞三种流场进行数值仿真及试验验证.Yang［18］等考虑到配送活动中顾客时间窗的不确定性，通过分析路径偏差、服务时间偏差、成本偏差和车辆在扰动时的位置，建立了针对客户时间窗变化的扰动恢复模型，并提出了一种基于禁忌搜索的调度方法.宋晓琳［19］等建立了直道和弯道的期望路径模型，采用高斯分布描述随机采样点，引入启发式搜索机制，改进RRT 算法，并将该算法应用在进行汽车壁障局部路径规划中.

综上，为了解决如何将骑手所关心的目标考虑在内、取送交叉的配送模式下如何为骑手分配路径、面对众多扰动因素时算法应如何调整等问题，本研究对取送交叉和考虑骑手扰动因素下的外卖配送路径优化问题进行深入研究.首先在问题描述方面，本研究不仅考虑了取送交叉的配送方式，并将骑手在配送过程中面临的中途接单、临时交通管制、商家出餐时间异常和顾客取餐时间异常四种扰动因素考虑在内，实现了取送交叉的配送方式下考虑多种扰动因素的外卖配送路径实时优化.其次在模型构建方面，本研究在常用目标函数运输成本和时间惩罚成本的基础上，增加了骑手空驶距离成本和骑手等待时间成本，充分将骑手的目标考虑在内，构建了外卖配送路径实时优化模型.最后在算法设计和算例分析方面，本研究设计了改进的自适应大邻域搜索算法，实现了取送交叉和多种扰动因素下的算法改进.并通过饿了么的实际算例，分别对不同算法、不同配送方式和不同扰动因素下的骑手配送路径优化方案进行了详细的算例分析，验证了模型和算法的有效性.

1 问题描述与模型构建

本章建立了取送交叉下的外卖配送路径优化模型.1.1 节介绍了取送交叉下，考虑骑手扰动因素的外卖配送路径实时优化问题描述.1.2 节是模型假设与符号说明.1.3 节以骑手空驶距离成本、运输成本、骑手等待时间成本和时间惩罚成本作为目标函数.考虑到骑手载重约束、时间窗约束和其他可行性约束，建立了外卖配送路径实时优化模型.

1.1 问题描述

在考虑骑手取送交叉和多种扰动因素的外卖配送路径实时优化中，待配送的订单动态实时产生，骑手需要根据配送的订单完成取送餐服务，需保证对于同一笔订单而言，取餐节点在前，送餐节点在后.具体配送流程如图1所示.

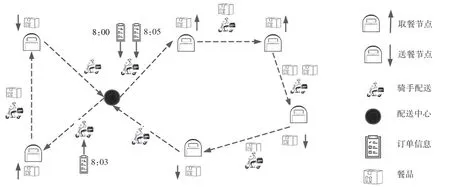
图1 取送交叉下考虑扰动因素的外卖配送示意图Fig.1 Takeaway delivery route considering disturbance under the integration of pickup and delivery

由图1 可以看出，骑手通过取送交叉的配送方式完成已分配订单的配送（即可以先去多个取餐节点取餐，再去多个送餐节点送餐），同时在配送过程中会动态产生新的订单.另外，骑手在配送过程中，可能会面临扰动因素，此时需要根据骑手现有订单完成情况对骑手配送路径进行改派.其中，骑手面临的扰动因素主要有以下几个方面.

1）骑手中途接单：当骑手已分配配送路径后，接到新的订单，需要将新订单插入到骑手分配好的路径中.

2）临时交通管制：骑手在配送途中面临交通管制是指算法原有为骑手规划的配送路径无法行驶，此时需要调整当前配送方案，重新为骑手规划路径.

3）商家出餐时间异常：商家出餐时间异常是指商家无法在规定的时间内出餐，影响骑手的配送效率.此时骑手可以选择原地等待或先去其他节点完成取送餐任务.

4）顾客取餐时间异常：顾客取餐时间异常是指顾客无法在规定的时间内取餐，影响骑手的配送效率，例如无法联系顾客等情况.此时骑手同样可以选择原地等待或先去其他节点完成取送餐任务.

1.2 模型假设与符号说明

根据问题描述，本节设计了假设条件并对模型中的符号进行说明.假设条件具体如下：1）骑手、商家节点和顾客节点之间的距离已知，顾客节点的时间窗和需求量已知；2）所有骑手采用同款车型，最大载重、最远行驶距离、平均行驶速度均已知且为固定常数；3）单位骑手空驶成本、单位时间惩罚成本、单位运输成本和单位骑手等待成本和商家平均出餐时间等系数均已知且为固定常数.外卖配送路径优化模型的符号说明如表1所示.

表1 符号说明Tab.1 Symbol description

1.3 模型构建

本文以骑手空驶距离成本、运输成本、骑手等待时间成本和时间惩罚成本作为目标函数，将外卖平台、骑手和顾客的目标综合考虑.各个目标函数具体如下.

1）骑手空驶距离成本：指骑手由前一节点到商家节点空驶所产生的成本，骑手的空驶距离是指骑手由前一节点去取餐节点间的距离.骑手空驶距离成本可表示为：

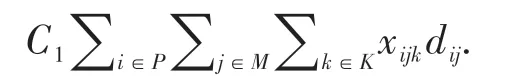
2）运输成本：指骑手配送过程中产生的时间成本、电力成本等，一般与骑手配送的总行驶距离相关.运输成本可以表示为：

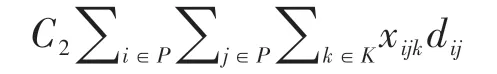
3）骑手等待时间成本：指由于骑手到达顾客节点的时间早于顾客约定的最早到达时间ei，或骑手到达商家节点的时间早于商家的出餐时间时，骑手等待所产生的成本.骑手等待时间成本可以表示为：

4）时间惩罚成本：指由于骑手的送达时间晚于顾客约定的最晚送达时间窗li时，顾客差评或取消预订等操作带来的销售损失机会成本.当顾客差评或取消订单时，外卖平台会损失一定的利润，同时信誉受到影响，骑手的服务分数会降低，同时还需缴纳平台的罚款.时间惩罚成本可以表示为：

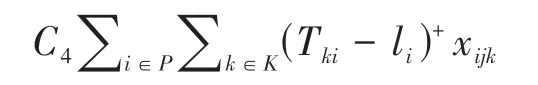
另外，在约束条件构建方面，参考了已有外卖配送路径优化研究中的骑手载重约束、时间窗约束、负载平衡约束和其他可行性约束.根据目标函数和约束条件，外卖配送路径优化模型构建如下：

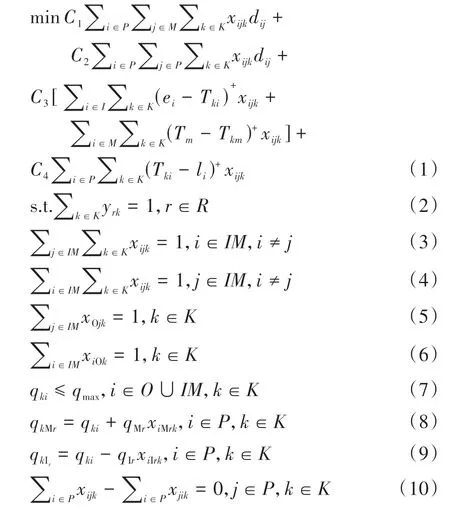
目标函数（1）由骑手空驶成本、运输成本、时间等待成本和时间惩罚成本组成，期望实现总成本最小化.式（2）表示对于每个订单而言，必须有骑手完成其配送工作.式（3）和式（4）表示对于已经分配给骑手的订单，每个商家节点和顾客节点都被骑手访问且每个节点仅访问一次.式（5）和式（6）表示每个骑手均从配送中心出发，最终回到配送中心.式（7）表示骑手可容纳的最大载重量限制，即骑手在离开所有节点时，其载重量不能超过最大载重量.式（8）和式（9）为载重量的递推公式，当前一节点为取餐节点时，骑手载重量等于现有载重量加取餐量；当前一节点为送餐节点时，骑手载重量等于现有载重量减送餐量.式（10）表示流量平衡约束，即所有节点到达和离开的骑手数相同.式（11）表示对于每一个已经分配给骑手的订单而言，其取餐节点和送餐节点必须由同一个骑手进行访问.式（12）～式（15）为时间约束.其中，式（12）表示对于已分配订单r而言，骑手到达商家节点的时间早于到达顾客节点的时间，即骑手必须先取餐后送餐.式（13）和式（14）表示时间的递推关系，即骑手到达某一节点的时间等于骑手到达前一商家节点的时间、骑手等待时间和行驶时间之和.式（15）为变量的取值范围.

2 算法设计

从外卖配送路径实时优化模型中可以看出，外卖配送路径优化模型属于NP-hard 问题.当问题规模增大时，计算量也随之增长，精确算法往往很难在有效时间内求解.考虑到外卖配送具有数据体量大、数据动态产生且对于路径规划速度有较强要求等特点，本文设计了改进的自适应大邻域搜索算法.该算法主要借鉴了贪婪算法和自适应大邻域搜索算法（Adaptive Large Neighborhood Search，ALNS）［20］，通过贪婪算法生成初始解，通过多种算子完成邻域搜索提高解的质量.

由于外卖配送属于实时优化问题，且本研究考虑了取送交叉的配送模式和骑手面临的扰动因素，本研究在算法方面分别针对具体问题进行了改进.针对外卖配送中订单动态分配问题，在算法中增加了连续场景的构建，实现骑手配送路径的动态实时优化；针对取送交叉下的外卖配送特点，在路径的生成方式中增加了解的可行性判断，保证了对于同一笔订单而言，取餐节点在前，送餐节点在后；针对骑手面临的扰动因素，算法分别设计了骑手中途接单、顾客取餐时间异常、商家出餐时间异常和临时交通管制四种扰动因素下的改进操作.通过针对算法的改进，有效实现了外卖订单和骑手的高效匹配和动态实时优化.该算法的具体阐述如下.

2.1 算法描述

该算法主要包括生成初始骑手配送方案、分配方案的邻域搜索和动态调整邻域搜索方式权重三个部分.同时为了避免搜索过程陷入局部最优，本算法采用模拟退火算法的准则作为判断依据，将重构后的解的目标函数F′与重构之前的解的目标函数F进行比较，设定解的接受概率为e-(F′-F)/T.同时增加了取送交叉下邻域搜索的可行性判断和骑手面临扰动因素时的算法改进.该算法的主要框架如表2所示.

表2 改进的自适应大邻域搜索算法框架Tab.2 Improved adaptive large neighborhood search algorithm framework

2.2 生成初始分配方案

本节设计了改进的贪婪算法生成初始解.其总体思路如下：首先，依据配送任务的产生时间将任务进行排序，并确定当前场景下有哪些骑手可以完成该订单的配送任务；其次，确定各个骑手完成该笔订单所需的骑手空驶距离成本，依据空驶距离成本最小化的目标将该订单分配给骑手.最后，将该笔订单的商家节点和顾客节点随机插入当前骑手的配送路径方案中，但需保证骑手先去商家节点取餐，再去顾客节点送餐的顺序.

2.3 任务的插入与替换

任务的插入与替换通过多个订单移除算子和多个订单插入算子完成对骑手配送路径的邻域搜索.由于订单插入时要考虑骑手配送过程中的取送交叉，因此在订单插入后需要加入可行性判断这一流程.各个流程具体阐述如下.

2.3.1 订单移除算子

本文分别设计了随机移除和最差移除两种移除算子，每次任务移除首先通过轮盘赌选择移除方案，每个算子均从可以移除的任务集合R中移除q笔订单.本文定义了两种移除算子：1）随机移除算子.该移除算子随机从可以移除的任务集合R中移除q笔订单.该方法操作简单，有助于搜索过程的多样化并可以跳出局部最优解.2）最差移除算子.其方法是根据模型中目标函数中F的计算方式，计算骑手已分配任务方案中各个任务的目标函数值，并将目标函数值最差的q个任务进行移除.

2.3.2 订单插入算子

经过订单移除后，这些订单将被重新插入各服务资源的任务安排队列中，实现邻域搜索并获得新的可行解.每次任务插入操作同样通过轮盘赌选择插入算子.每种插入算子都是从当前解s中插入q笔订单.1）随机插入算子：该算子随机将移除的q笔订单插入解s中.该方法同样操作简单，有助于搜索过程的多样化并可以跳出局部最优解.2）贪婪插入算子：根据任务最少结束时间贪婪插入，该算子对于随机移除的q笔订单，分别计算其插入各个服务资源的任务安排队列中的任务结束时间，选择使该订单任务结束时间最短的服务资源和队列位置将订单进行插入，具体插入方式与生成初始解的方式相同.

2.3.3 取送交叉下的可行性判断

取送交叉下，任务的移除和任务的插入过程中均需要用到可行性判断，从而保证对于同一笔订单而言，骑手可以先去商家节点取餐，再去顾客节点送餐.

在任务移除中，不同于静态的任务分配问题，外卖的配送路径优化问题是动态进行的.在移除前首先要做的是判断当前场景下可以移除的任务集合R.其判断条件是不能移除已经服务完成和正在服务的任务，只可以对未开始服务的任务进行移除.在任务的插入过程中，同样要判断是否可行，要判断插入后，是否满足对于同一笔订单而言，骑手先去商家节点取餐再去顾客节点送餐的顺序，同时插入过程需尽可能满足骑手的负载均衡条件.

2.4 动态调整邻域搜索方法权重

对于每种邻域搜索算子而言，每次迭代通过轮盘赌的方式，根据各个算子的累积分数，在多种任务移除方式和任务插入方式中选择一种插入方式和移除方式进行邻域搜索.轮盘赌的取值范围取决于每种方式在之前迭代中累加分数.当该算子在之前迭代中搜索效果较好时，该算子累加分数较高，在当前迭代中有更高的概率被选中；反之，当该算子在之前迭代中搜索效果较差时，其累加分数较少，在当前迭代中被选中概率较低.

具体分数累加的过程如下.首先为各个调整方式设定初始分数均为1，按照该规则进行分数累加：1）如果该方法产生新的全局最优解，则其摧毁算子和插入算子的分数分别增加θ1；2）如果该方法产生比上一次迭代更好的解，但并非所有迭代中的最优解，则其摧毁算子和插入算子的分数分别增加θ2；3）如果该方法未找到比上一次迭代更好的解，但是模拟退火准则e-(F′-F)/T为所接受的解，则其摧毁算子和插入算子的分数分别增加θ3；4）如果该方法得到的解未满足模拟退火准则，则其摧毁算子和插入算子的分数分别增加θ4.其中θ1＞θ2＞θ3＞θ4，第i个算子在第j+1次迭代中的权重如式（13）所示：

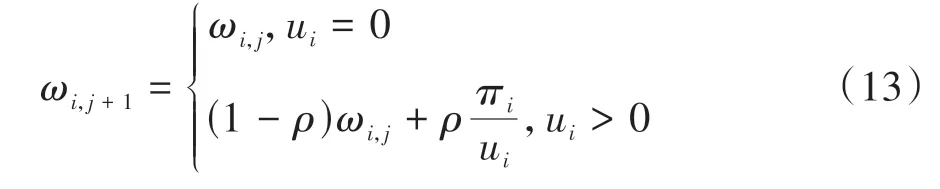
其中，ωi，j为第j次迭代中第i个算子的权重，πi为第i个算子在之前迭代中所累积的分数，ui为第i个算子的总使用次数，ρ为权重更新系数，ρ∈[0，1]，该系数可以控制该算子上次迭代系数和该算子的累积分数在本次迭代中的权重.通过以上方式，实现了对于邻域搜索方式权重的动态调整.

2.5 考虑骑手扰动因素下的算法改进

骑手在配送中面临扰动因素时，其配送路径需要针对不同的扰动做出相应的改进.本节分别考虑了骑手中途接单、临时交通管制、商家出餐时间异常和顾客取餐时间异常四种扰动因素，分别针对各种扰动因素对本文所提出的算法进行改进，具体如下.

1）骑手中途接单：骑手中途接单时的情况分为两种，一种为骑手存在已取餐但未送餐的订单，另一种为骑手不存在已取餐但未送餐的订单.对于第一种情况，算法需要将骑手未送餐的订单、未配送的订单和新插入的订单放入路径分配集合中，并进行邻域搜索，得到骑手新的配送路径；对于第二种情况，算法只需要将新订单插入骑手未配送的订单集合中，并进行邻域搜索得到骑手新的配送路径.

2）临时交通管制：临时交通管制下，两节点间将产生不可通行路段.此时算法将骑手从当前位置去原有路径分配方案中下一个节点的路径作为不可行路径，对骑手未配送路径重新进行邻域搜索，得到新的配送方案.新方案可以保证骑手从当前位置到下一个节点间的路径可行.

3）商家出餐时间异常：商家出餐时间异常下，算法将出餐时间异常的商家节点和该笔订单对应的顾客节点取出，根据商家出餐异常时间，重新插入骑手未完成配送的路径中，生成骑手新的配送路径的初始解.在插入过程中同样需要进行多次邻域搜索，不仅保证商家节点在前，顾客节点在后的顺序，同时也保证得到一个效果较好的满意解.

4）顾客取餐时间异常：顾客取餐时间异常时，算法根据顾客异常时间，将当前顾客节点重新插入骑手未完成的路径优化方案中，生成新配送路径方案的初始解.在插入过程中同样需要进行多次邻域搜索，保证解的质量.

3 算例分析

本节对外卖配送路径优化问题进行算例仿真分析，算例生成方式主要借鉴2020年3-5月，饿了么的“智慧物流：新冠期间饿了么骑手行为预估”大数据比赛，模拟了边长为3 km×3 km 的方形外卖配送区域内，周期为两小时的外卖高峰期订单数据.本算例所使用的计算机硬件环境为2.5GHz i5-2520M CPU，8GB RAM 以及Windows 系统，并运用Python3.7.4 编写代码.假设外卖平台每一分钟更新一次新产生的订单信息和骑手信息，并进行订单分配和骑手路径规划，两小时内产生了120 组场景的数据.改进的自适应大邻域搜索算法的具体参数如表3所示.

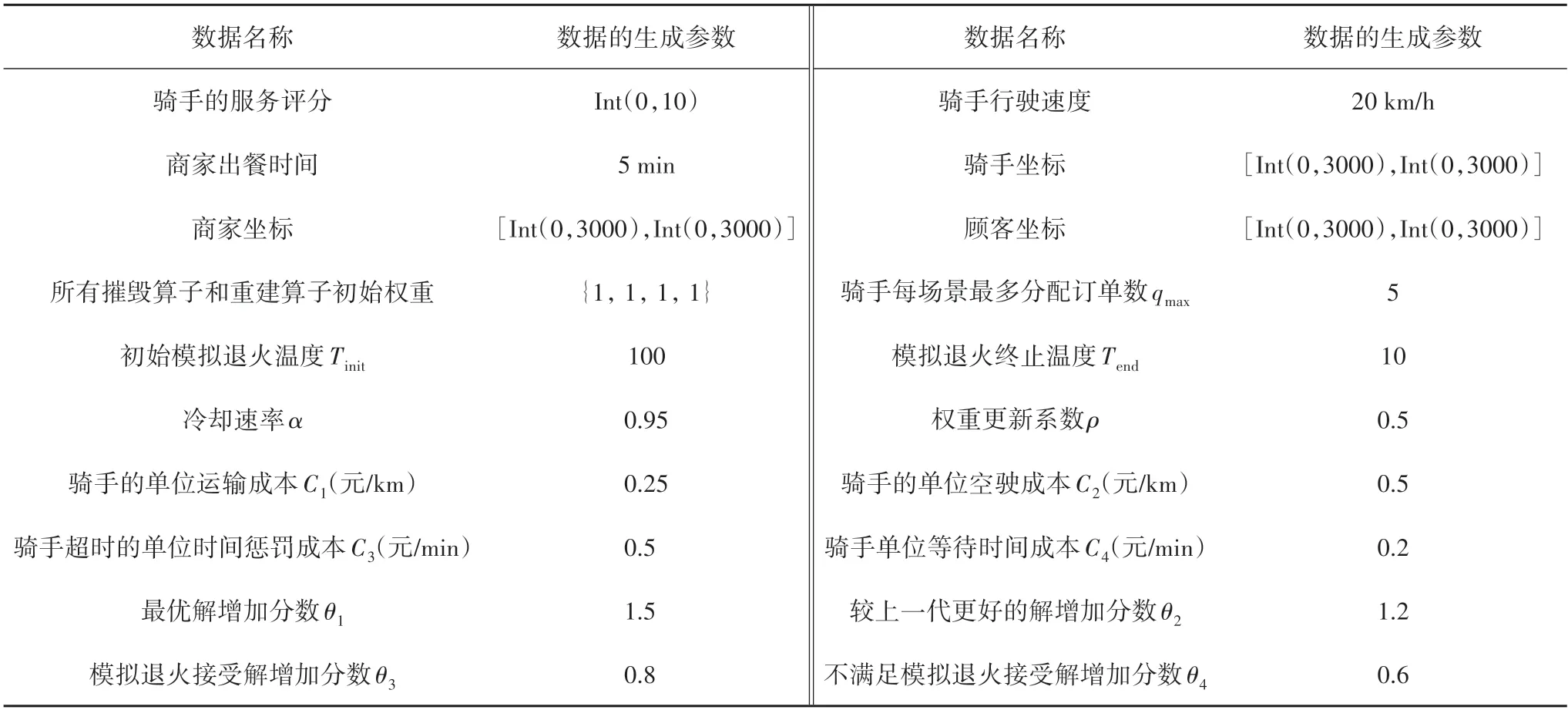
表3 算例分析中的所有参数Tab.3 All parameters in the numerical experiment

3.1 不同算法的计算效果对比分析

本节基于骑手空驶距离成本的贪婪算法、遗传算法和改进的自适应大邻域搜索算法对高峰期两小时内所有分配路径的总目标函数值的计算效果进行了对比，结果如表4 所示.另外，骑手在场景一的配送路径和各个骑手的目标函数值如表5 所示，（1）～（4）分别代表骑手空驶距离成本、运输成本、骑手等待时间成本和时间惩罚成本.配送路径中的数字代表骑手需配送的订单编号，数字产生的顺序代表骑手的配送顺序，例如编号6表示第6个订单的商家节点，编号6’表示第6 个订单的顾客节点.另外，改进的自适应大邻域搜索算法在场景一中的收敛速度如图2 所示，图3 为场景一中骑手1 和骑手2 的配送路径，其中虚线路径为骑手1，实线路径为骑手2，场景一中骑手1 和骑手2 均从配送中心O出发，开始配送任务.

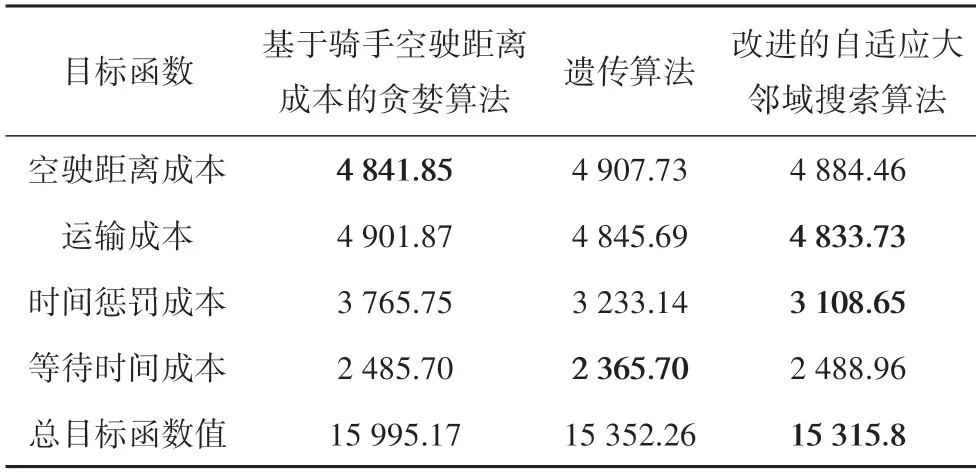
表4 不同算法的计算效果对比Tab.4 Comparison of computational effects of different algorithms

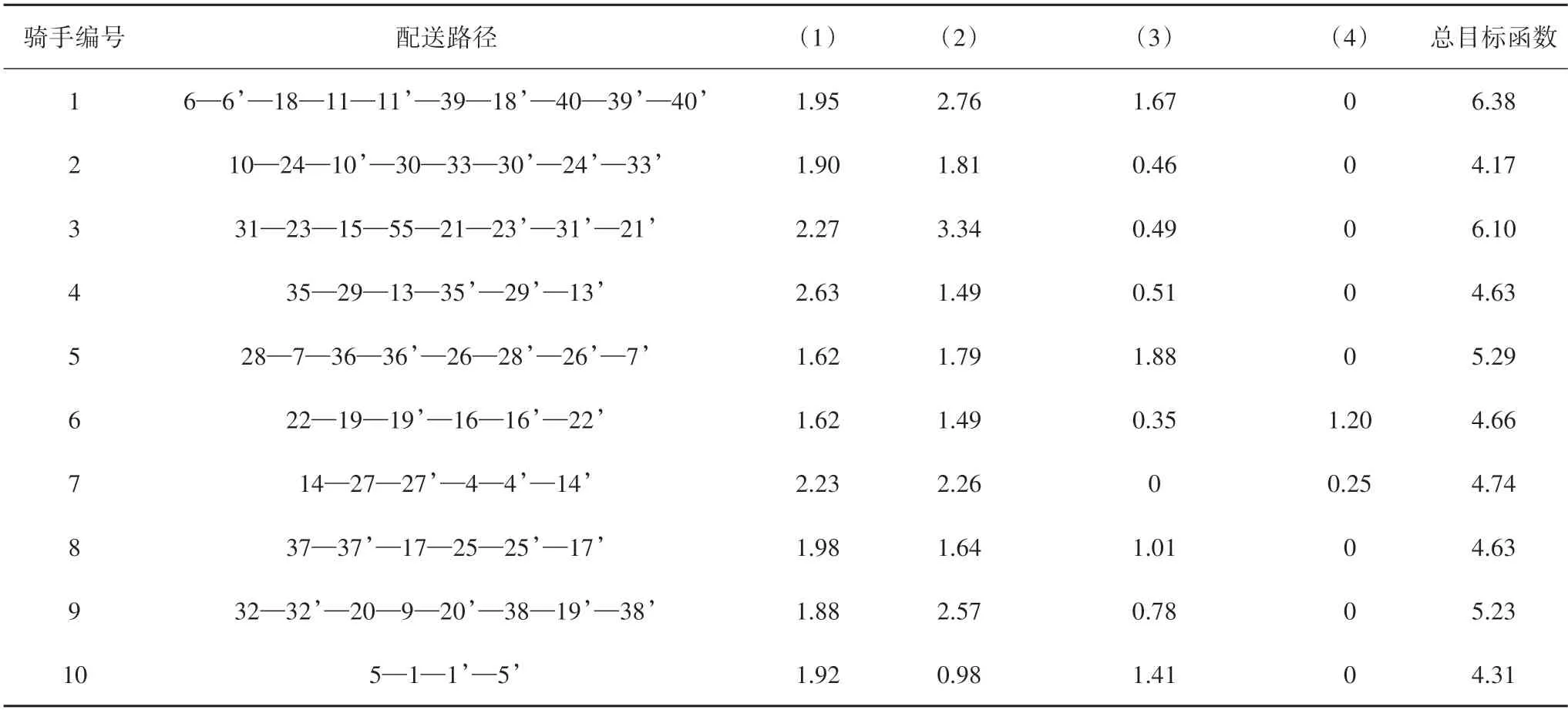
表5 场景一的骑手配送路径Tab.5 Rider delivery route in the first scenario

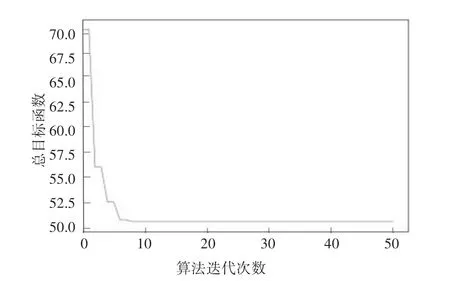
图2 改进的自适应大邻域搜索算法在场景一的收敛图Fig.2 Convergence figure of improved ALNS algorithm in the first scenario

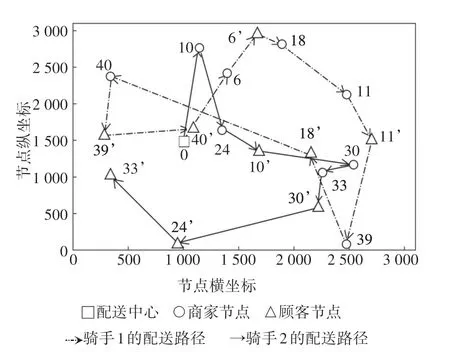
图3 场景一中部分骑手的配送路径图Fig.3 Pickup and delivery route of some riders in the first scenario

从表4和表5的算例结果中可以看出，本文提出的改进的自适应大邻域搜索算法可以有效求解取送交叉下外卖配送路径实时优化问题，且在运输成本、时间惩罚成本和总成本方面均优于基于骑手空驶距离成本的贪婪算法和遗传算法.另外，通过改进的自适应大邻域搜索算法进行路径规划时，其主要成本来自运输成本和空驶距离成本，减少了由于超时带来的时间惩罚成本.

从图2 中可以看出，改进的自适应大邻域搜索算法在第10 次迭代次数前已经收敛，其收敛性能较强.从图3 中可以看出，改进的自适应大邻域搜索算法通过允许取送交叉的配送方式，有效实现了骑手与待服务订单的合理路径优化.

3.2 考虑扰动因素下的算例分析

本节在场景一骑手1 的配送路径优化方案的基础上，分别添加四种扰动因素，观察扰动因素对骑手配送方案的影响.四种扰动因素的具体设计如下.

1）骑手中途接单：当骑手去11 号节点取餐后，将41号订单分配给该骑手，其中41号节点的商家坐标为（416，164），顾客节点的坐标为（2 478，240）；2）临时交通管制：当骑手去11 号订单的取餐节点取餐后，11 号订单的送餐节点与取餐节点间临时交通管制（即编号11 无法通行到11’）；3）商家出餐时间异常：假设订单编号为11 的商家节点出餐时间异常；4）顾客取餐时间异常：假设订单编号为11 的顾客节点11’取餐时间异常.四种扰动因素设计下，算例分析结果如表6所示.

由表6 可知，相比于未考虑扰动因素的正常配送路径而言，扰动因素的产生会使配送总成本增加.扰动因素产生时，本文提出的改进的自适应大邻域搜索算法通过对已分配路径的部分顺序进行调整和邻域搜索，使原有骑手配送路径的总成本仅小幅度增加，有效实现了骑手面临中途接单、临时交通管制、商家出餐时间异常和顾客取餐时间异常等扰动因素时的外卖配送路径实时优化.

表6 考虑扰动因素下的计算效果对比Tab.6 Comparison of computational effects of different algorithms considering disturbance factors

3.3 不同配送方式下的算例分析

本节同样以场景一中骑手1 的配送路径优化方案为例，通过改变骑手的配送方式，将取送交叉的配送方式、依据订单号成对插入的配送方式和先全部取餐再全部送餐的配送方式进行对比，观察不同配送方式对于总成本的影响.对比结果如表7所示.

从表7 中不难发现，取送交叉的配送方式要优于先全部取餐再全部送餐的配送方式和根据订单号成对配送的配送方式.可见，取送交叉的配送方式对于取送餐节点的选择更加灵活，通过减少配送节点取送顺序约束，从而有效降低了总配送成本，同时也使外卖配送路径优化方案更加符合现实情况.

表7 不同配送方式下配送路径与成本的对比Tab.7 Comparison of delivery routes and costs under different delivery modes

4 结论

经过数十年的发展，我国外卖行业规模不断扩大，但目前对于动态实时优化、取送交叉和考虑扰动因素下的外卖配送路径优化研究仍不充分.因此，本文对取送交叉下考虑多种扰动因素的外卖配送实时路径优化问题进行深入研究.首先，在常用目标函数运输成本、时间惩罚成本的基础上，设计了骑手等待时间成本和骑手空驶距离成本，将骑手所关心的目标考虑在内，构建了外卖配送路径优化模型.其次，通过设计多种邻域搜索算子，将取送交叉的配送方式和骑手面临的扰动因素考虑在内，设计了改进的自适应大邻域搜索算法.最后，通过算例分析验证了模型和算法的有效性，并得出结论.

算例分析得到的具体结论如下：1）改进的自适应大邻域搜索算法在运输成本、时间惩罚成本和总成本方面均优于基于骑手空驶距离成本的贪婪算法和遗传算法，该算法可以有效求解取送交叉下外卖配送路径实时优化问题.2）扰动因素的产生会使配送总成本增加.本文提出的改进的自适应大邻域搜索算法通过对已分配路径的部分顺序进行调整和邻域搜索，使原有骑手配送路径的总成本仅小幅度增加，有效实现了骑手面临中途接单、临时交通管制、商家出餐时间异常和顾客取餐时间异常等扰动因素时的外卖配送路径实时优化.3）当骑手采用取送交叉的配送方式时，其总成本要优于先全部取餐再全部送餐的配送方式和根据订单号成对配送的配送方式.这是由于取送交叉的配送方式通过减少配送节点取送顺序约束，从而有效降低了总配送成本.

本研究同样具有一定的局限性，例如由于算例分析中节点众多，未能在有效时间内通过精确算法计算出外卖配送路径优化问题的最优解，因此只与贪婪算法和遗传算法等常用启发式算法进行算例结果对比.未来的研究可充分将启发式算法与深度强化学习等新技术相结合，设计更为高效的算法，以求解外卖配送路径优化问题.