黏土与粉土复合地层及其中地铁隧道的车致长期沉降

马龙祥 ，靳永福 ，张 超 ，汪 乐

（1. 西南交通大学土木工程学院， 四川 成都 610031；2. 无锡地铁集团有限公司，江苏 无锡 214100；3. 华设设计集团股份有限公司，江苏 南京 210014）

近年来，随着地铁运营时间的不断增长，我国各大城市的地铁隧道都出现了一定程度的长期沉降.由此不仅可能会诱发结构开裂，而且会加剧轨道的不平顺程度，严重影响地铁的乘车舒适度，对地铁的结构安全及运营质量也会产生极为不利的影响[1-3].研究表明，列车振动荷载长期循环往复的作用是影响地铁隧道运营期间长期沉降最为重要的因素之一[4].因此，对地铁列车振动荷载作用引起隧道长期沉降的研究具有重要的现实意义及工程价值.

针对列车荷载长期作用诱发地铁隧道及其地基的长期沉降问题，国内外学者已开展了一定的研究：王湛等[4-6]建立地铁隧道的平面应变模型，以拟静力法计算地铁列车引起隧道地基的动应力，进而结合相应饱和软黏土在循环荷载作用下的不排水累积变形模型及累积孔压模型，计算了地铁隧道地基的长期沉降；高广运等[7]建立了交叉隧道的三维有限差分模型，以人工数定激励力模拟列车荷载，计算得到了列车动荷载作用下上海地区软黏土的变形和应力分布规律；张冬梅等[8]考虑了地下水对长期沉降量值的影响，建立了动力流-固耦合计算模型，进而结合经验拟合模型分析了列车荷载对隧道及周围软土长期沉降的影响规律；曾二贤[9]通过建立轨道-隧道-大地系统的2.5 维有限元数值分析模型，计算了列车移动荷载作用下地基土的动力响应，进而分析了地铁运行引起的地基长期沉降并研究了列车速度、衬砌刚度及厚度等参数对其的影响. Huang 等[10]基于饱和黏土的循环迁移模型，考虑动力荷载及土体固结对沉降的贡献，采用土-水完全耦合动力有限元方法研究获得了饱和黏土中地铁隧道由列车荷载诱发的长期沉降及其发展规律.

综上所述，对列车荷载作用下隧道及其地基长期沉降的研究，目前已取得了一定的成果，但主要集中在软黏土地基中，而对于粉土、低塑性黏土及两者形成的复合地层地基的研究较少. 虽然这些地基由列车荷载引发长期沉降的量值小于软土地基，但实践表明这些地基中的地铁隧道也会发生一定程度的车致长期沉降，进而给地铁隧道的维保及列车运营带来不利影响. 在此背景下，本文以无锡市某地铁区段为研究对象，通过建立该区段轨道-隧道-地层耦合系统的2.5 维数值模型，分析了运行列车诱发地铁隧道下覆低塑性黏土及粉土复合地层的动应力响应规律，进而结合循环荷载作用下低塑性黏土及粉土的不排水累积变形特征及孔压累积特征，研究并明确了列车振动荷载长期作用诱发该复合地层及其中地铁隧道的长期沉降量值及发展规律. 本文的研究成果对类似地层中地铁运营诱发地基及隧道结构长期沉降的评估及防治具有一定的参考价值.

1 依托工程概况

无锡地铁1 号线起至惠山新城的堰桥站，终点为滨湖区的雪浪站，全长29.42 km. 自2014 年7 月1 日开通运营后，部分下覆地层为黏土（低塑性）及粉土的盾构隧道区段出现了一定量值的长期沉降.由于此区段地铁隧道无明显渗漏水现象且周边并未进行过大型工程的建设，初步断定隧道的长期沉降主要由列车振动荷载的长期作用所导致. 为了明确此区段在地铁列车荷载长期作用下的沉降特征，选取一具体的典型区段展开研究. 所选研究区段长约150 m，隧道埋深约为15.5 m，管片内径2.75 m，外径3.10 m，左右线中心距离约为13 m，地层自上往下依次为杂填土、黏土、粉质黏土夹粉土、粉土夹粉质黏土、粉质黏土、黏土、粉土，其中隧道埋置于粉土地层之上的低塑性黏土层及粉质黏土层中. 在该研究区段，地下水位长期处于第一层杂填土与下一层黏土的交界面附近，在具体分析时认为地下水位恰好处于杂填土与黏土的交界面，水位距地表1.7 m.根据地勘资料，地下水位以下较深深度范围内的土体均可视为饱和土体. 此外，该区段采用普通整体道床轨道，钢轨为T60 轨，扣件为DTVI2型扣件（刚度为40 MN/m, 阻尼为30 kN·s/m），运行车辆编组为6 节编组B 型车，列车轴重为14 t，运行速度为80 km/h.

2 复合地层及地铁隧道长期沉降计算模型

列车振动荷载作用诱发隧道及其地基的长期沉降可以分为土体不排水累积塑性应变引发的沉降以及土体累积孔压消散产生的固结沉降[5]. 首先计算运行列车引发复合地层的动应力响应，以此为基础，结合相应土体在循环振动荷载作用下的累积变形及累积孔压发展特征，采用分层总和法来分别研究复合地层及其中的地铁隧道由列车长期运营诱发的上述两部分沉降.

2.1 隧道地基土动应力响应的计算

由于单趟列车运行致使土体产生的塑性应变很小，本文在计算单趟列车通过引起隧道地基土的动应力响应时，将土体合理地近似为线弹性体，而地基土的塑性性能将由循环振动荷载作用下相关土体的不排水累积变形特性来体现. 此外，由于循环振动荷载作用下地基土动力累积变形及累积孔压特征多以地基土总应力为控制指标，本文在分析地基动应力响应时采用水土合算的总应力法，对于地下水位以下的饱和土体取其饱和密度进行计算. 如此处理虽然有一定程度的简化，但在很多类似的研究中均取得了较好的效果[8-9,11-12].

基于上述考虑，忽略研究区段地层在水平面上的起伏及地铁区间隧道的纵坡，将大地近似简化为水平成层介质并视轨道-隧道-地层系统为沿线路纵向不变的一致性系统，进而采用2.5 维方法[9,11]对列车荷载作用下的隧道地基土动应力响应进行研究.具体地，钢轨被视为Euler 梁，采用2.5 维解析方法进行模拟，扣件采用沿线路纵向连续分布的弹簧-阻尼单元模拟，道床、隧道及土体介质采用黏弹性本构模型进行描述，并使用2.5 维有限元法进行模拟，而解析的钢轨模型通过扣件处的位移与力平衡条件与隧道-地层有限元模型实现耦合. 在计算分析中，依据研究区段中部地勘资料确定地层的分层，地层及隧道的具体物理力学参数取值见表1，其中隧道埋置于粉土地层之上的黏土层及粉质黏土层中，隧道下方地基由2 m 厚的（低塑性）黏土层及足够厚的粉土层组成. 据此建立的轨道-隧道-地层耦合系统的2.5 维概化数值模型见图1 （由于钢轨为解析模型，该图仅对地层及隧道结构的有限元区域进行了示意）. 在该概化模型中，计算范围在宽度方向上取80 m（模型中线距左右侧边界距离各取40 m），在深度方向上取50 m. 为了避免振动波在计算边界产生过大反射以影响计算范围内动力响应计算的精度，在计算边界设置2.5 维一致黏弹性人工边界，其刚度及阻尼按式（1）、（2）进行设置[13].

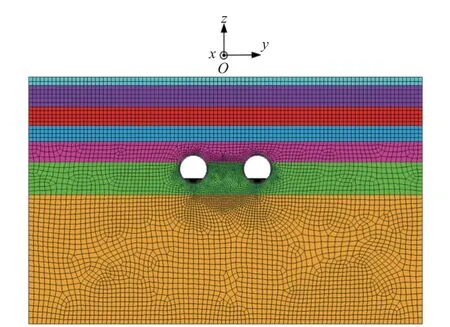
图1 2.5 维数值模型Fig. 1 2.5-dimensional numerical model

表1 地层及隧道结构的物理力学参数Tab. 1 Physical and mechanical parameters of soils and tunnel structure

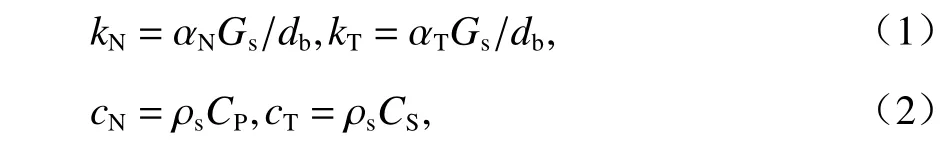
式中：kN、kT、cN和cT分别为法向刚度、切向刚度、法向阻尼和切向阻尼； αN和 αT分别为黏弹性边界法向及切向的修正系数，在本研究中，分别取其建议值1.33 和0.67[13]；Gs、 ρs、CP和CS分别为边界位置相应土体的剪切模量、密度、P 波波速和S 波波速；db为激励源到边界的距离，近似取受列车荷载作用的隧道道床中心到相应边界的垂直距离.

由于轨道不平顺产生的动态轮轨力对隧道地基的动应力影响有限，在研究运行列车引起地基土的响应时，可将移动列车荷载考虑为由地铁列车各轮轴轴重组成的准静态荷载，即移动列车荷载可表示为

式中：x为线路纵向坐标；t为时间；Nw为列车的总轮轴数；Fj为列车第j轴的半轴重； δ (·) 为Dirac 函数；dj为列车第j轴与第一轴之间的距离；v为列车运行速度；x0为初始时刻列车第一轴的纵向坐标.

在本文的具体分析中，设定分析断面（拾振断面）的纵向坐标x=0 ，并设定初始时刻列车第一轴距分析断面的距离为25 m，即初始时刻列车第一轴的纵向坐标x0取为 -25 m.

2.2 黏土及粉土不排水累积变形及累积孔压特征

列车振动荷载长期作用下隧道地基土的沉降主要由循环振动荷载作用下土体不排水累积变形特征及孔压累积特征决定. 对于黏土及粉土的不排水累积变形特征，可采用Chai 等[14]提出的模型进行描述，如式（4）.

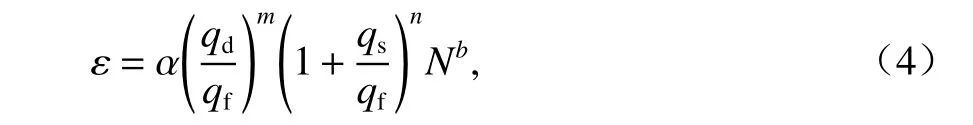
式中： ε 为土体不排水累积应变；qd为动偏应力；qs为静偏应力；N为荷载循环次数；n、 α、m、b为根据对黏土或粉土在不同qd、qs、qf条件下进行的循环动三轴试验中得到不排水累积应变-振次曲线进行拟合而得到的拟合参数，依据文献[14-15]，对于研究区段涉及的低塑性黏土，取n= 1， α =1.10，m=2.0 ，b=0.16 ，对于研究区段的粉土，取n=1 ， α =0.64 ，m=1.7，b=0.10 ；qf为土体静强度，如式（5）.

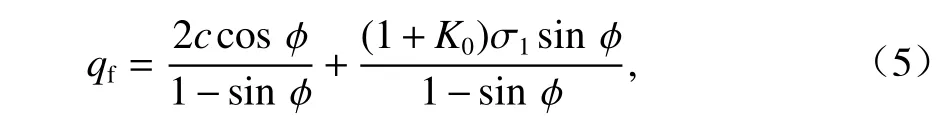
式中：c、 φ 分别为土壤黏聚力及内摩擦角； σ1为前期固结压力；K0为土体的侧限系数.

另一方面，黏土在循环振动荷载作用下的孔压累积模式为[5]

式中：u为累积孔压；为土体平均有效固结压力； ξ1、n1、 β1为根据对黏土在不同D*条件下进行的循环动三轴试验中得到孔压-振次曲线进行拟合而得到的拟合参数，依据文献[5,15]，可取为ξ1=0.002 3，n1=2.19 ， β1=0.66；D*为 相 对 偏 应 力 水平，如式（7）[16].

式中：Ds=qs/qult，为静偏应力水平，Dp=(qs+qd)/qult，为峰值偏应力水平，qult为土体不排水极限强度；Dmax为可能达到的最大偏应力水平，即Dmax=1 .

粉土在循环振动荷载作用下的孔压累积模式可描述[17]为

式中： ξ2、f2、g2、 β2为根据对粉土在不同qd、qs、qf条件下进行的循环动三轴试验中得到孔压-振次曲线进行拟合而得到的拟合参数，依据文献[17]，可取为 ξ2=5.4，f2=1.9，g2=1 ， β2=0.1 .

2.3 长期沉降的计算

结合列车运营引发隧道地基土的动应力响应及循环振动荷载作用下地基土的动力累积变形特征和累积孔压特征，使用分层总和法[5-7]可以计算出地基土长期沉降的发展规律. 具体步骤为

步骤1建立相应的静力三维数值模型，按总应力法求解隧道地基土在自重荷载作用下的静应力张量.

步骤2结合隧道地基土在单次列车荷载作用下的动应力响应及自重荷载作用下的静应力响应，分别计算运行列车荷载作用下地基土的动偏应力水平以及自重荷载作用下地基土的静偏应力水平. 其中，动偏应力水平以列车中部到达分析断面为准进行计算，而偏应力水平q可依据相应应力张量由式（9）计算得到[11].

式中：J2为第二偏应力不变量.

步骤3将隧道下覆地基土进行分层（层数需取足够多，且地层交界面必须取为层间界面），依据相应土层的类型，按式（4）计算相应土层由土体不排水累积变形引发的长期应变，按式（6）或式（8）计算相应土层中的超静孔隙水压力累积量值.

步骤4在求得各层土体的不排水累积应变及累积超静孔隙水压力量值后，采用分层总和法按式（10）及式（11）分别计算列车振动荷载引发隧道下覆特定深度位置处土体不排水累积变形导致的沉降Sd及由累积孔压消散导致的固结沉降Sv，其中，Sv采用Terzaghi 一维固结理论[16]进行求解.

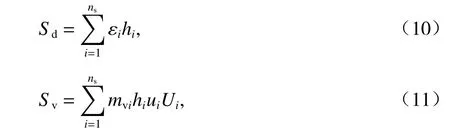
式中：ns为模型最下面的土层分层至隧道下覆特定深度位置处土层分层的总分层数； εi为第i层土体的不排水累积应变；hi为第i层土的厚度；mvi为第i层土的体积压缩系数，取mvi=1/Esi，Esi为相应土层的压缩模量；ui为第i层土的不排水循环累积孔压；Ui为第i层土的固结度，对于长期沉降可偏保守地认为孔压完全消散[5]，取Ui=100% .

步骤5列车振动荷载作用下土体不排水累积变形导致的沉降以及累积孔压消散导致的沉降相加即可得到地基土的总沉降S.

对于隧道结构的长期沉降，由于隧道结构相较于地层的刚度很大，忽略隧道结构在沉降过程中可能产生的横断面变形对其整体量值的影响，近似认为其整体量值及发展与其拱底正中紧邻位置处地基土的长期沉降相同，即可按上述方法进行相应计算及分析.

由于研究地铁区段左右线间距较大，本文在隧道及其下覆地基的沉降分析中，仅考虑关注侧隧道内列车长期运营的影响.

3 计算结果分析

图2 给出了列车在左侧隧道内运行时紧邻左侧隧道拱底正中部位地基点的动应力响应时程. 图中：σxx、 σyy、 σzz分别为纵向正应力、横向正应力、垂向正应力； σxy、 σyz、 σzx分别为垂向切应力、横向切应力、纵向切应力； σ1、 σ2、 σ3分别为运行列车诱发的最大主应力、中主应力、最小主应力.

从图2（a）中可以看到：列车轮轴的通过对关注点的应力响应有重要影响，关注点处的应力时程波形会明显出现与各轮轴到达时刻相对应的峰值；在近隧道位置，地铁列车通过引发的垂向正应力 σzz比其他应力分量更大，尤其在列车中部到达研究断面时刻，垂向正应力能够达到纵向或水平向正应力的2 倍 ～ 3 倍；运行列车引发的切应力 σxy与 σyz量值几乎为0，但列车引发的沿线路纵向的切应力 σzx具有较大的量值.

由于纵向正应力 σxx与纵向切应力 σzx具有较大量值，因此，在分析列车荷载长期作用诱发土体变形时不宜忽略其对土体动偏应力的影响. 由此也可进一步得出，由于无法考虑 σxx与 σzx的效应，采用平面应变模型难以对运行列车荷载作用下土体的长期变形及沉降进行较为准确的分析. 由图2（b）可知：紧邻左侧隧道拱底正中部位地基点在列车中部到达时刻（t= 3.654 s）前后较长的一个时间范围内均处于三向受压状态，各主应力时程曲线大致关于列车中部到达拾振断面时刻呈对称分布，其中附加最小主应力 σ3（即附加最大压应力）量值最大可达-3.8 kPa.

图2 运行列车作用下地基土的动应力响应Fig. 2 Dynamic stress response of foundation soil under the moving train

由第2 节分析可知，地铁振动荷载作用下地基土中的附加动偏应力水平是影响地层车致长期沉降的决定性因素，因此，有必要对列车运行引发地层动偏应力的空间分布规律及随时间的变化规律进行研究. 图3 给出了列车在左侧隧道中运行时，左侧隧道拱底正下方地基土不同深度处动偏应力的时程及典型时刻左侧隧道拱底正下方地基土动偏应力沿深度的分布规律.

由图3 可知：地基土的动偏应力随列车驶近驶离拾振断面的过程先增大后减小，且其时程关于列车中部到达拾振断面时刻（t= 3.654 s）大致呈对称分布；当前条件下，隧道正下方地基土动偏应力的最大量值约为2.80 kPa；不同时刻隧道下覆复合地层附加动偏应力沿深度具有相似的分布规律，但动偏应力的最大量值出现在列车中部到达时刻附近；在隧道下覆的复合地层中，随着深度的增加，附加动偏应力先增大后减小，其最大量值出现在隧道底部以下约1.3 m 处；隧道下覆复合地层中动偏应力沿深度方向的衰减在距隧道10 m 的范围内较为迅速，而在距隧道10 m 范围外较为缓慢. 在列车中部到达时刻，地基土动偏应力在隧道下方10 m 处已从该时刻地基土动偏应力的最大量值2.80 kPa 衰减到了1.37 kPa，衰减了约51%.

图3 隧道正下方不同位置土体的动偏应力水平Fig. 3 Dynamic deviatoric stress levels of foundation soils at different positions under the tunnel

图4 为列车运行次数与沉降（由土体不排水累积塑性应变导致的沉降、由累积孔压消散导致的沉降、总沉降）的发展规律. 由于模型的对称性，此处不对左线及右线隧道进行专门区分，分析所得结论同时适用于左、右线隧道（后文针对隧道结构及其地基土长期沉降的分析亦同）.

由图4 可知：

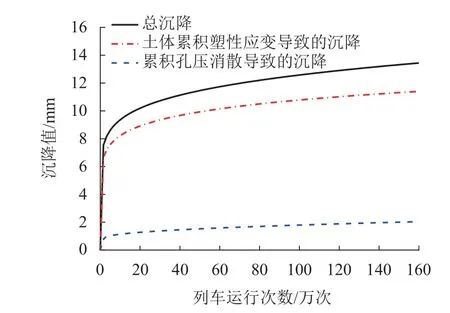
图4 隧道结构模拟长期沉降的发展及组成Fig. 4 Development and compositions of the simulated long-term settlement of tunnel structure

1） 在黏土与粉土复合地层中，列车振动荷载诱发隧道结构的长期沉降随着运营时间的增加呈非线性增大，在列车运行的前20 万次内该沉降发展较为迅速，随后沉降的累积发展较为缓慢且沉降量值逐步趋于稳定；

2） 在列车运行160 万次后，列车振动导致的隧道总沉降已基本趋于稳定，其量值为13.44 mm，在列车仅运行20 万次后，列车振动导致的总沉降量值就可达到10.20 mm，约占沉降基本稳定后总沉降量值的76%；

3） 在黏土与粉土复合地层中，由土体不排水累积塑性应变导致的隧道结构沉降较大，而由土体累积孔压消散导致的隧道结构沉降相对较小. 在列车运行160 万次后，由土体累积塑性应变导致的隧道结构沉降量值为11.40 mm，约占总沉降的85%，而由累积孔压消散导致的沉降量值为2.04 mm，仅约占总沉降的15%. 可见，土体不排水累积塑性应变仍是低塑性黏土与粉土复合地层中车致沉降的主要诱因.

图5 为不同因素导致隧道沉降占比随时间的变化情况. 由图5 可知：随着时间的增加，由土体不排水累积塑性应变导致的隧道沉降占总沉降的比例在地铁运营初期的一个较短时间内（大约为列车前1 万次运行期内）会先出现一定的增加，而后将不断减小；由累积孔压消散导致的沉降占总沉降的比例在地铁运营初期则会先出现一定的降低，而后不断增大；从总体上讲，两个因素导致沉降的占比随时间的变化并不剧烈，即在隧道总沉降量值中的占比总体较为稳定.

图5 不同因素导致隧道沉降占比随时间的变化Fig. 5 Changes of proportions of tunnel settlements caused by different factors in the total settlement with time

图6 给出了地铁运行160 万次后（即土体变形基本稳定后）隧道正下方地基沉降（由土体不排水累积塑性应变导致的沉降、累积孔压消散导致的沉降、总沉降）沿深度的分布规律.

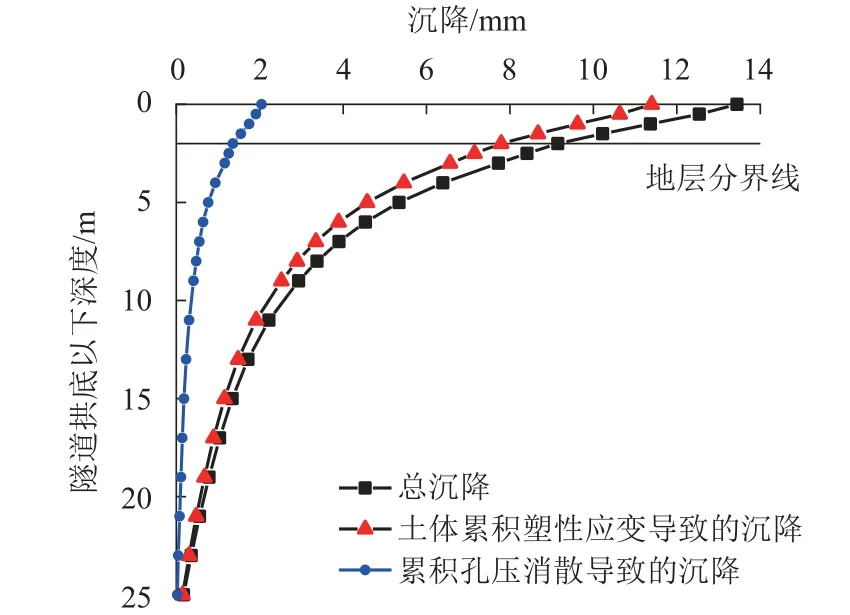
图6 列车荷载引发地基土长期沉降沿深度的分布规律Fig. 6 Distribution of long-term settlement of foundation soil caused by train load along depth

由图6 可知：随着深度的增加，地基土的总沉降量值逐渐减小，在隧道拱底处，地基土总沉降为13.44 mm，而在隧道下方5、8、15 m 处，地基土总沉降量值分别降低至5.34、3.38、1.34 mm，降低幅度分别达60%、75%、90%.

通过进一步的分析，还可以得到如下结论：1） 随着深度的增加，地基土总沉降的衰减速度逐步放缓；2） 地基土总沉降量值沿深度的衰减在隧道下方5 m 范围内较为迅速；3） 隧道下覆地基土沉降主要发生在距隧道拱底15 m 的深度范围内；4） 由土体不排水累积塑性应变及累积孔压消散导致的沉降沿深度的分布规律与总沉降极为相似，并且在深度方向上表现出与总沉降近乎一致的衰减速度. 在隧道拱底处，由土体不排水累积塑性应变导致的地基土沉降与由累积孔压消散导致的地基土沉降分别为11.40、2.04 mm，而在隧道下方5、8、15 m 处，前者分别降低至4.57、2.90、1.15 mm，降低幅度分别达60%、75%、90%，后者分别降低至0.77、0.48、0.19 mm，降低幅度分别达62%、76%、91%.

图7 为不同因素导致的地基土沉降占比沿深度的变化. 由图7 可知：由土体不排水累积塑性应变及累积孔压消散导致的地基土沉降占其总沉降的比例随深度的变化并不明显，在隧道下覆25 m 范围内，由前者导致的沉降占总沉降的比例稳定在85%左右，而由后者导致的沉降占总沉降的比例则稳定在15%左右.

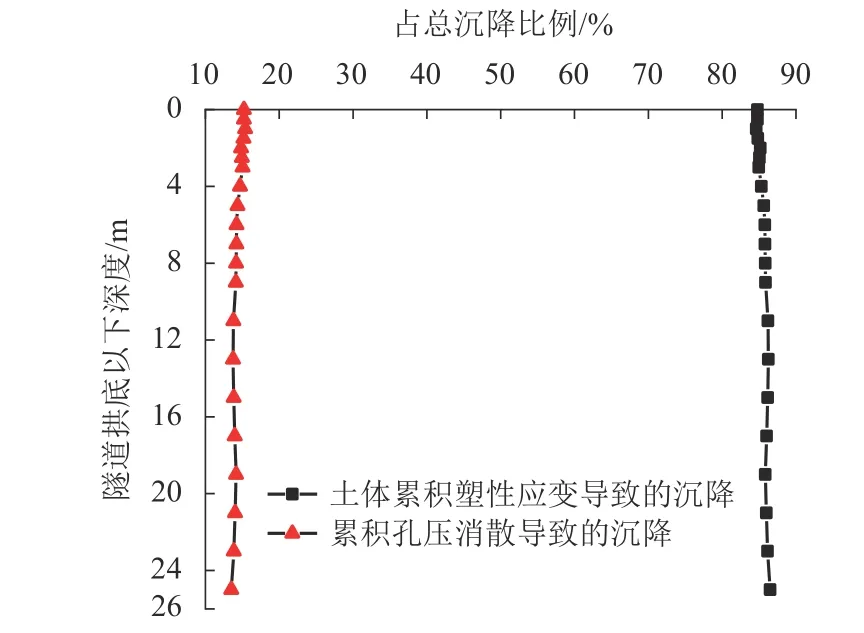
图7 不同因素导致的地基土沉降占比沿深度的变化Fig. 7 Changes of proportions of settlements caused by different factors in the total settlement with depth

4 计算与实测结果的对比分析

为了探明地铁区间隧道的长期沉降特征，无锡地铁公司针对地铁1 号线区间隧道组织开展了长期沉降的监测工作. 该工作通过对布设在隧道衬砌拱脚附近观测点的高程进行精密水准测量得以实施.在监测中，监测控制网采用国家一等水准精度观测，沉降变形监测点按Ⅱ级垂直位移监测网技术要求布设成闭合水准路线进行观测. 同时，为了确保结构长期沉降监测的准确性，长期监测沿用了建设期的高程系统，从而保证了地铁隧道结构建设与运营期高程系统的一致性. 隧道结构长期沉降监测点均布设在隧道管片结构的拱脚位置附近，采用L 型沉降测量标志用电钻引孔打入衬砌结构中，如图8 所示. 在所研究区段，沉降监测点按每50 m 的间距进行布设，并在地铁运营前即通过精密水准测量获得了监测点的初始高程. 在地铁随后的头5 年运营期内，相关单位对研究区段总计进行了6 次沉降观测，其中前三次的观测时间分别约为地铁开通运营后7 个月、14 个月及23 个月，而后三次的观测时间均与其前一次的观测时间间隔约12 个月.

图8 地铁隧道结构长期沉降监测点Fig. 8 Monitoring point for long-term settlement of metro tunnel

为了验证本文理论分析结果的可靠性，将研究区段隧道结构在线路运营前5 年间的模拟总沉降与区段内3 个测点的实测沉降进行对比，如图9 所示.研究区段单侧隧道中列车1 年的运行次数依据无锡地铁实际情况按4.5 万次计.

图9 隧道结构长期沉降模拟值与实测值的对比Fig. 9 Comparison between simulated and measured long-term settlements of tunnel structure

由图9 可知：1） 区段内3 个测点的实测结构沉降发展规律较为一致，均表现出运营初期迅速发展而后缓慢发展的趋势. 虽然3 个测点位于线路纵向150 m 范围内的同一区段，但由于地质条件在空间上的变异性（3 个测点位置处各土层层厚等地质条件有所差异），实测结构沉降在量值上依然存在一定的差异. 2） 3 个测点运营前3 年内的实测沉降要略小于模拟值，而运营约4 年及5 年后的实测沉降值则接近或略大于模拟值.

造成如上差异主要有如下原因：1） 概化的数值模型依据的研究区段中部地勘资料将地层简化为水平成层介质并忽略了区间隧道的纵坡，并不能完全准确反映研究区段地质条件的空间变异性及地铁隧道结构的实际性状；2） 实际隧道结构发生的长期沉降往往是纵向不均匀的沉降，其将诱发隧道结构产生一定程度的横断面变形[18]（如椭圆化），而理论计算忽略了隧道的横断面变形，并以隧道拱底正中紧邻位置处地基土的长期沉降表征隧道整体沉降，势必在结果上会与以隧道拱脚附近测点为基准的实际监测（如图8 所示）存在一定差异；3） 对比中没有考虑无锡地铁1 号线在前5 年运营中每日开行列车次数的变化，只是使用了运营前5 年内年平均开行列车次数作为比对依据，而无锡地铁1 号线在实际运营的前2 年内每年开行列车次数实则小于5 年的年平均开行列车次数；4） 理论模型忽略了隧道施工期对土体扰动及运营期可能存在的轻微渗漏水等对隧道长期沉降的影响，而这些影响在实际中虽然对研究区段隧道长期沉降不起决定性作用，但存在的可能性仍较大.

尽管研究区段地铁隧道结构长期沉降的实测值及模拟值存在一定的差异，但从总体上讲，无论是在发展规律还是在量值上均吻合得较好. 由于测点2与测点3 处的实际地质情况相较于测点1 与概化数值模型揭示的地质状况更为接近，在这些位置实测得到的隧道结构沉降也与理论模拟值更为吻合. 综上可见，本文针对低塑性黏土与粉土复合地层及其中隧道结构车致长期沉降问题所建立的理论分析模型及所做仿真分析的可靠性均得到了较好验证，因此相关研究成果具有较大参考价值.

5 结 论

本文在充分考虑列车荷载行进特征的基础上，建立了移动列车荷载作用下轨道-隧道-地层耦合系统动力响应求解的2.5 维数值模型，分析了运行地铁列车诱发下覆黏土及粉土复合地层的动应力响应规律，进而结合循环荷载作用下黏土及粉土的不排水累积变形特征及累积孔压特征，计算得到了列车振动荷载作用下黏土与粉土复合地层及其中隧道结构的长期沉降量值及发展规律. 通过与地铁隧道实测长期沉降的对比得到了验证. 通过研究，得到了以下主要结论：

1） 运行列车诱发隧道下覆地基土的动偏应力沿深度方向先增大后减小，而在所考虑的黏土与粉土复合地层地基中，其最大量值可达2.80 kPa，出现在隧道拱底下覆约1.3 m 深度处.

2） 平面应变模型难以实现对列车振动荷载长期作用诱发地基沉降的准确分析，不宜采用.

3） 在黏土与粉土复合地层中，列车振动荷载诱发隧道结构的长期沉降主要发生在列车的前20 万次运行期内，在该时间段内，隧道结构产生的长期沉降最少可占最终稳定沉降量值的70%.

4） 在黏土与粉土复合地层中，隧道结构的车致长期沉降在地铁列车运行160 万次后基本趋于稳定，其量值可达13.44 mm，其中由土体不排水累积塑性应变引起的沉降为11.40 mm，占比85%，由累积孔压消散引起的固结沉降为2.04 mm，占比15%.

5） 隧道下覆黏土与粉土复合地基长期变形主要发生在隧道下方15 m 范围内，该范围内的土体沉降对隧道结构长期沉降量值的贡献占比达90%.