组合铝合金模板的有限元分析
2022-11-03张世伟童思远武港港
张世伟, 童思远, 武港港
(中建铝新材料河南有限公司, 河南 鹤壁 458000)
引言
铝合金模板在混凝土结构施工过程中,要独立承受相应的荷载并满足承载力、刚度和稳定性的要求[1]。由于相关要求在混凝土达到设计要求强度的50%时方可拆模(这个时间一般为7 d),因此模板使用的时间较短,并且要求快速安装、拆卸方便、模板能重复使用。由于砼结构及其施工方法、机械设备、施工环境的复杂性会造成模板工程的复杂性和多样性,并且与钢模、木模等其他种类的模板同时使用,导致组合铝合金模板的力学模型的简化和建立尤为复杂,完全通过力学分析铝合金模板整体安全较为困难。因此,在组合铝合金模板的理论计算中采用了大量的简化分析,这种方法比较保守。
1 理论计算
1.1 混凝土侧压力计算(参考JGJ62-2008 建筑施工模板安全技术规范)
以层高为2.9 m 的模板工程为例,墙模板主要受力为混凝土的侧压力[1]。
混凝土体积质量γc=24 kN/m3,间墙高度H=2.9 m;β1为外加剂修正系数,不加外加剂为1.0,加外加剂为1.2,此处取1.2;β2为混凝土坍落影响修正系数,当坍落<30 mm 时取0.85,当坍落为50~90 mm 时取1.0,当坍落110~150 mm 时取1.15,此处取1.15。
凝土浇筑速度v=2 m/h;混凝土温度t=25 ℃;温度修正系数=5;最大混凝土侧压力F=γcH=69.6 kPa,F=0.22γct0β1β2=51.52 kPa,两者取小值,F 的理论值应为51.52 kPa;有效压头高度h==2.15 m。
1.2 铝合金模板墙板挠度计算
铝合金模板一般为400 mm 宽;其截面截面惯性矩Ix=964 240 mm4;所受最大载荷W=51.52×0.4=20.61 kN/m;跨度L=600 mm;铝模板弹性模量E1=70 000 MPa。
受力简图如图1 所示,墙板最大挠度位置应出现在间距700 mm 处,该处荷载为梯度荷载,可以把最大载荷作为均布荷载进行简化计算。
1.3 横向背楞(双拼60×40×2.5)计算
按简支梁验算背楞时,背楞间距600 mm 作为计算宽度,近似按均布载荷计算。对拉螺栓间距800 mm;其截面参数Ix=468 600 mm4;跨度L=800 mm。
计算载荷W=51.52×0.6=30.91 kN/m;钢背楞弹性模量E2=206 000 MPa。
需要注意的是:
1)在对铝模板进行挠度计算的时候,并未考虑横向加筋,因此在实际施工过程中铝模板的挠度应小于理论计算值。
2)背楞实际承受的是墙柱模板边框传递的集中载荷,上述计算采用了均布载荷的计算方法,这是因为背楞一般为多跨连续梁,采用单跨简支梁均布载荷模型是可以接受的。在实际应用中,当背楞只有一跨时,为消除上述简化带来的不安全因素,应按集中载荷验算背楞的强度和变形。
2 有限元分析
有限元分析是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。因为实际问题被较简单的问题所代替,所以这个解不是准确解,而是近似解。由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。当今有限元分析软件的一个发展趋势是与通用CAD 软件的集成使用,即在用CAD 软件完成部件和零件的造型设计后,能直接将模型传送到CAE 软件中进行有限元网格划分并进行分析计算。
2.1 导入有限元分析软件
把需要计算的模型导入有限元分析的软件,并赋予其材料属性,我们本次分析的是铝模板和钢背楞,所以材料属性选择6061-T6 和合金钢。软件自带的材料中并没有钢背楞的实际材料Q235,由于金属材料受力后的位移只与弹性模量相关,与金属材料的含碳量及含其他元素量无关。因此,为了计算准确,我们选择与Q235 有相同弹性模量的合金钢。
2.2 常见的相触面
1)无穿透:用于静态算例、掉落测试算例和非线性算例。此接触类型可防止不同实体间产生干涉,但允许形成缝隙。此选项求解非常耗时。
2)允许贯穿:适用于静态算例、非线性算例、频率算例、扭曲算例及掉落测试算例。将不同实体的接触面视为不相连。对于静态算例和非线性算例,允许载荷在零件之间产生干涉。
3)接合:适用于所有需要网格化的算例类型。该程序会接合不同实体,适用于有多个焊接实体存在时的情况。
因此,在本次分析中我们对铝模板和钢背楞紧贴的两个面选择无穿透定义。
2.3 对铝模板和钢背楞进行夹具的定义
在工程实践中铝模板的边框紧邻另一块铝模板的边框,并由销钉、销片进行连接,实际上就限制了铝模板的六个自由度,在本次分析中通过限制模板边框的自由度来定义铝模板。钢背楞在工程实践中是多跨连续梁,但是在本次分析中我们按两端固定受两处集中载荷的静定梁处理。
2.4 定义外部载荷压力
由于混凝土的侧压力是随着深度的不同而增加,因此模板的受力是越靠下实际受力越大。根据受力简图建立压力方程,单位为N/m2。
2.5 对整个模型进行网格化
常规的规整几何模型是比较容易划分网格的,而在实际项目中,由于模型是复杂的几何,或是多个模型之间大小差异巨大,这种复杂的几何可能源自于SolidWorks 本身的设计图,也可能是别的三维软件所导出的stp 或者igs 等形式的中间格式。在本次分析中整体尺寸较大,而局部的小尺寸几何特征较多,因此,我们需要应用网格控制的手段,先把铝模板分为30 mm 的较大的网格。对于钢背楞,可以按照默认网格的方式。这样可以减少整个模型的网格数量,提高计算机分析的速度。
2.6 有限元分析计算
应用有限元分析软件,考虑铝模板横向加筋,并将铝模板和背楞进行整体性分析,计算两者的最大变形,如图2 所示。
3 结论
有限元分析与理论计算值产生差异的原因,见表1,一是由于有限元分析计算了横向加筋对铝模板的加强效果,二是钢背楞与铝模板的互相影响。
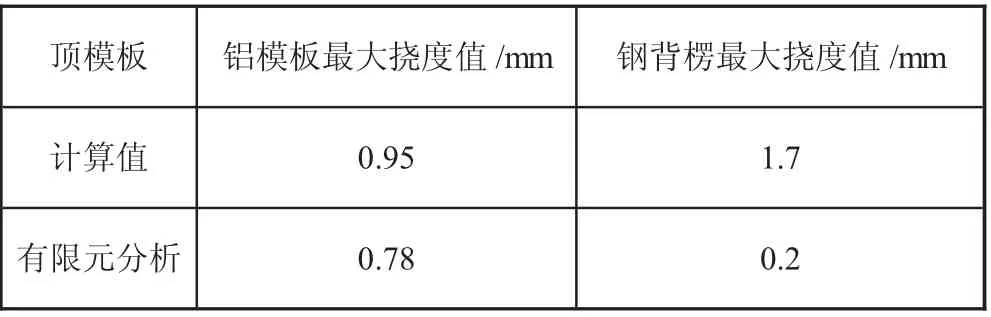
表1 有限元分析与理论计算值差异
本次分析并没有对应力进行对比分析,这是因为随着网格加密程度的增加,应力值也会发生变化,并逐渐稳定在某一固定值附近。如果需要计算相对准确的应力,就需要多次加密网格来进行计算。而位移值对网格密度的变化不那么敏感,因此,在满足许用应力和许用挠度的背景下,为了减小计算量,本文中并未给出应力值。
