空间变系数地理加权自回归模型的局部GMM估计

魏传华,王韶郡,苏宇楠

(中央民族大学 理学院,北京 100081)

一、引 言

近年来,空间数据分析与建模已经成为地理学、经济学、管理学等多个学科的热点问题。关于空间数据模型的介绍可参考Anselin等人的空间计量经济学类著作,以及Cressie等人空间统计学著作[1-6]。空间数据的两个最主要的特征是空间自相关性和空间异质性。对于空间自相关性的刻画,使用最多的是空间自回归模型,该模型是由Ord在Whittle的研究基础上得出的,一般记为[7-8]:

(1)

其中yi和xi=(xi1,xi2,…,xip)T分别是在第i个空间位置上的因变量和自变量观测值,β=(β1,β2,…,βp)T是p维待估未知系数,模型随机误差εi一般假设均值为0,方差为σ2。W=(wij)n×n为空间权重矩阵,用来刻画观测单元之间的连接关系,比如区域i,j之间如果相邻,则wij=1,否则为0。空间相邻的定义有多种,可以根据两个区域是否有共同的边来界定,更为一般的定义是基于空间距离、经济距离以及复杂社会网络中的关系等来确定。

对于空间异质性的处理,目前使用最多的是Brunsdon等提出的地理加权回归(Geographically Weighted Regression,GWR)方法[9]。GWR模型记为:

(2)

其中(ui,vi)是观测点的地理位置,ui表示经度,vi表示纬度;系数函数β(ui,vi)=[β1(ui,vi),β2(ui,vi),…,βp(ui,vi)]T是关于经纬度的未知光滑函数;其余符号与模型(1)的解释相同。这类空间变系数模型利用局部常数方法或者局部线性方法可以得到各个观测点上回归系数的估计值,从而可以直观描述某一具体系数函数随所研究的地理空间位置的变化情况,展示了空间关系的非平稳性,关于该模型的详细讨论可参考Fotheringham等的专著[10]。

对于空间自相关性和空间异质性,现有研究大都是对二者单独进行考虑和设定,将这两个因素同时考虑的研究相对较少。基于空间自相关设定和地理加权回归方法分别在刻画空间自相关性和空间异质性上的有效性,如何将两种建模方法结合起来处理两种空间性质引起了关注,在模型(1)、(2)的基础上,可以得到如下的空间自回归地理加权回归模型:

(3)

Fotheringham等最早基于实际例子对这种建模方法进行了简单讨论,但没有进一步对该模型的统计推断等问题进行研究。魏传华等对该模型进行了估计方法的讨论,提出了profile极大似然估计和两步估计方法,但是没有对所提估计量的性质进行深入的理论研究[11]。Sun等基于局部线性光滑和profile极大似然估计对模型进行了估计,并给出了所提估计量的渐近性质[12]。为了克服异方差性,Wei等基于Su的研究构造了模型的半参数广义矩估计(GMM)[13-14]。

(4)

我们将该模型称之为空间变系数地理加权自回归模型。对于模型(4),Geniaux和Martinetti在研究中提及了该模型,并针对包括该模型在内的多类模型介绍说使用工具变量方法进行估计,但没有对估计方法的细节进行详细介绍,而且该文中涉及的多类模型在模型形式上差别很大,需要深入讨论[15]。除此之外,就笔者所知,目前还没有针对性研究模型(4)的相关论文。需要指出的是,Wu等提出一类时空加权自回归模型,其因变量和自变量是在某一时间、某一空间位置上的观测值,具有时间和空间两个属性[16]。模型中自变量对应的回归系数和因变量滞后项对应的参数都设定为时间和空间的光滑函数,提出利用两阶段最小二乘估计和工具变量估计模型中的未知系数函数。Malikov和Sun提出了一类更为广泛的变系数空间自回归模型,其中滞后参数和回归系数设置为一般的协变量而不仅仅是模型(4)中所用的经纬度的光滑函数,并对模型提出了局部GMM估计,深入研究了所提估计量的渐近性质[17]。模型(4)是Wu、Malikov等人所研究模型的特殊形式[16-17]。

作为空间自回归模型和地理加权回归模型的推广,模型(4)能够同时刻画空间自相关性和空间非平稳性,是一类非常有用的空间数据分析模型。关于该模型的针对性研究,目前仅仅在Geniaux和Martinetti的研究中简单提及,对包括该模型在内的多种模型只介绍说可以用工具变量方法估计,但对于工具变量怎么选取以及怎么构造估计量等没有进行讨论[15]。针对这一半参数回归模型,本文主要使用局部GMM方法对模型进行估计,该方法在Malikov和Sun的研究中是作为一类简单估计方法进行了介绍[17],此外Cai、Tran等人采用类似的估计思想对动态变系数面板数据模型进行了估计[18-19]。本文对模型(4)这类复杂的空间变系数模型给出具体的估计步骤,并通过数值模拟考察不同设定下估计量的表现,最后使用该模型分析了一个实际例子。

二、模型的估计

为方便介绍,模型(4)记为如下的矩阵形式:

Y=ρ(u,v)WY+M+ε

(5)

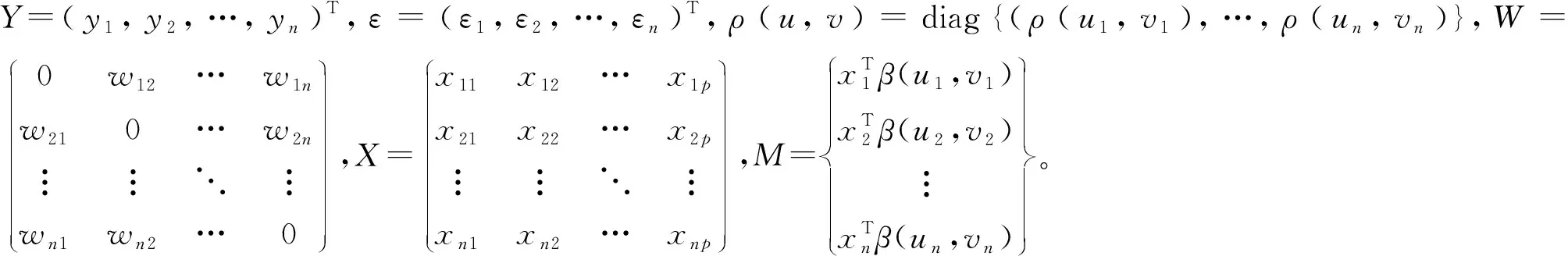
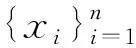
E[(WY)Tε]=E[(W(I-ρ(u,v)W)-1M)Tε+(W(I-ρ(u,v)W)-1ε)Tε]

(6)

即模型(5)中存在内生性问题,因此不能直接采用一般变系数模型的估计方法。下面介绍局部GMM方法,首先,将式(5)改写成如下形式:

(7)

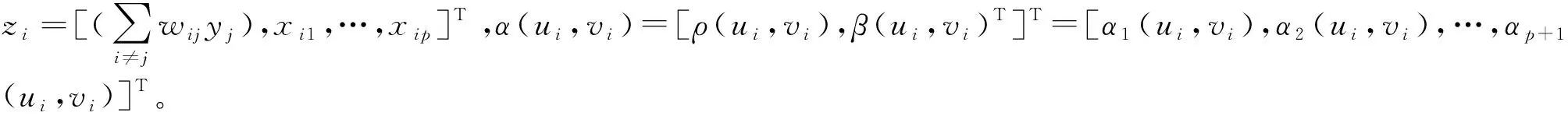
(8)

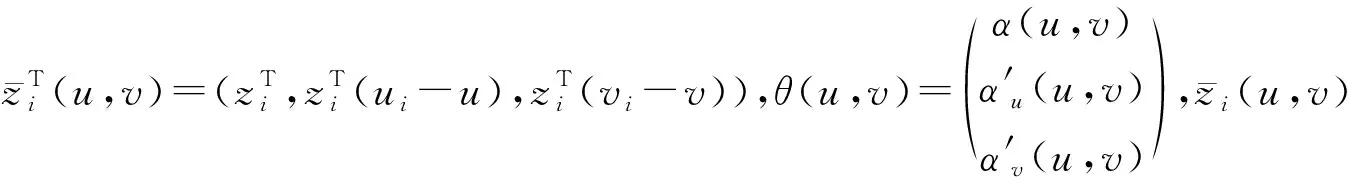
进一步可以得到:

(9)

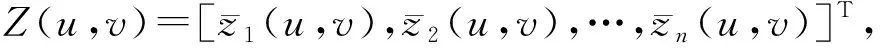
Y≈Z(u,v)θ(u,v)+ε

(10)

前面提到,模型存在内生性问题(空间滞后项存在内生性),当(I-ρ(u,v)W)-1存在时,有:

E(Y)=(I-ρ(u,v)W)-1M=(I+ρ(u,v)W+ρ2(u,v)W2+…)M

(11)

记R=(u,v),因此可以选择WX,WR,W2X,W2R,…作为WY的有效工具变量。

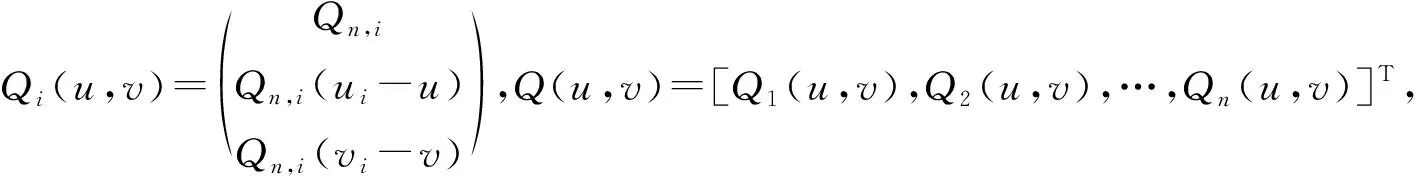
E[Q(u,v)TKH(u,v)(Y-Z(u,v)θ(u,v))]≈03d×1

(12)

其中核函数的对角矩阵KH(u,v)=diag{k1(u,v),k2(u,v),…,kn(u,v)},记:

gn(θ)=Q(u,v)TKH(u,v)(Y-Z(u,v)θ(u,v))

(13)

则θ(u,v)的局部GMM估计为:

(14)

V(u,v)是一个3d×3d的正定加权矩阵,简单计算后可以得到:

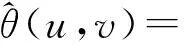
(15)

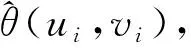
三、数值模拟

本节通过数值模拟方法考察空间变系数地理加权自回归模型的局部广义矩估计法在有限样本下的表现。

(一)数据生成

考虑如下模型:

(16)

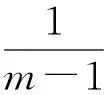
图1 Rook邻接示例

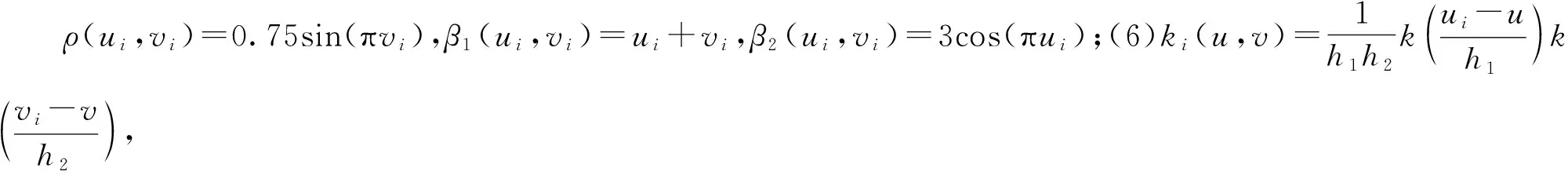
(a)直接选择单位阵I,估计结果为:

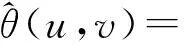
Z(u,v)TKH(u,v)TQ(u,v)Q(u,v)TKH(u,v)Y

(17)

(b)一步LGMM估计,参考Tran和Tsionas的做法,令V(u,v)=V0(u,v)=Q(u,v)TKH(u,v)Q(u,v),估计结果为[19]:

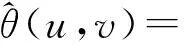
Z(u,v)TKH(u,v)TQ(u,v)V0-1(u,v)Q(u,v)TKH(u,v)Y

(18)

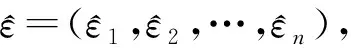
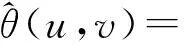
(19)

(二)模拟效果的指标评价

用均方根误差作为模拟效果的评价指标。对于每一个变系数函数,分别计算其均方根误差(RMSE):

(20)

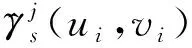
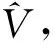
表1 不同样本量下的模拟结果

(三)变系数曲面图对比

绘出200次模拟得到变系数均值曲面和变系数的真实值曲面。受篇幅限制,这里只展示一组图片,即β1(ui,vi)的估计情况。

1.n=64时

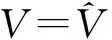
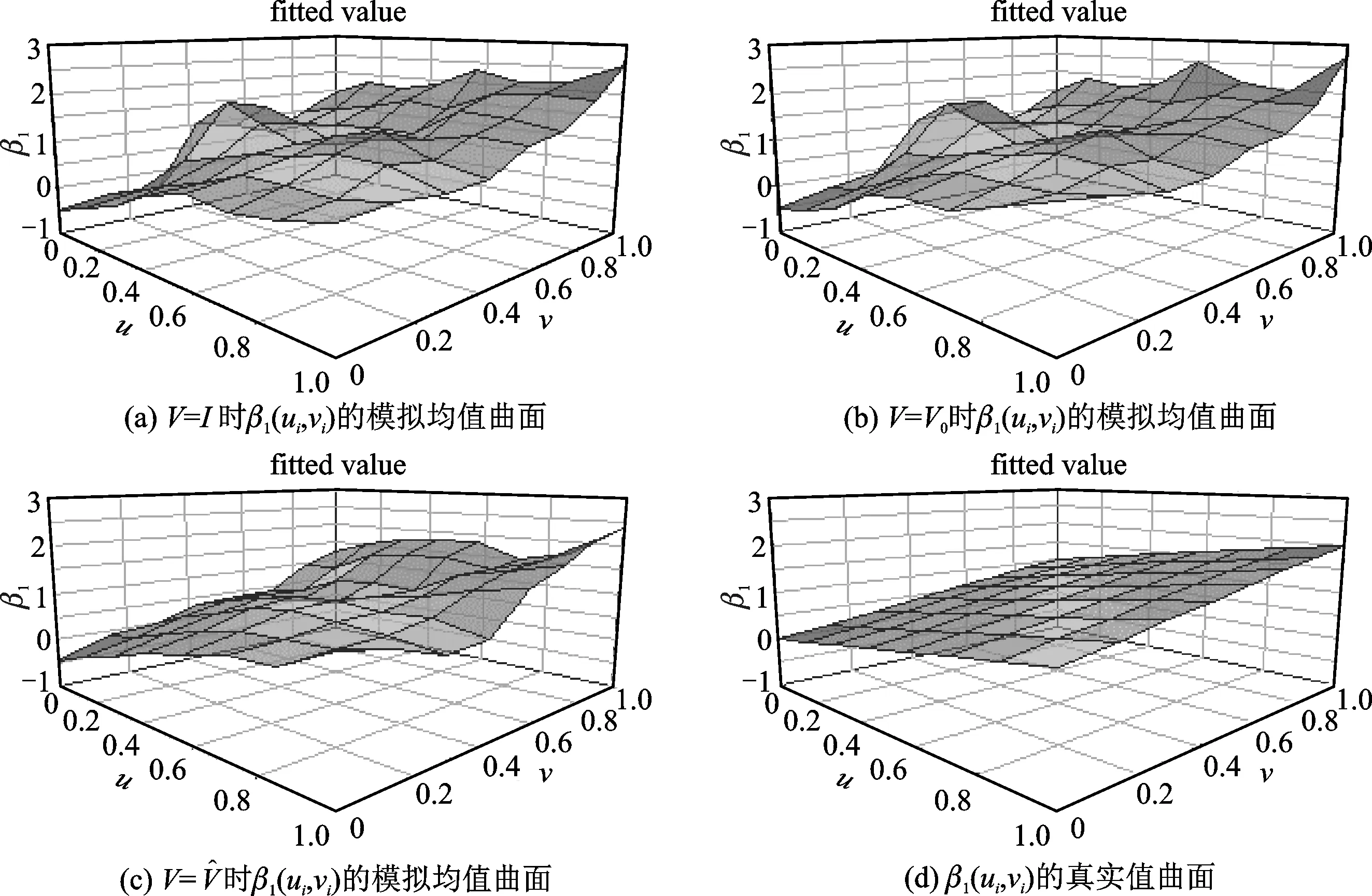
图2 n=64时,模拟均值曲面和真实值曲面

2.n=169时

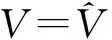
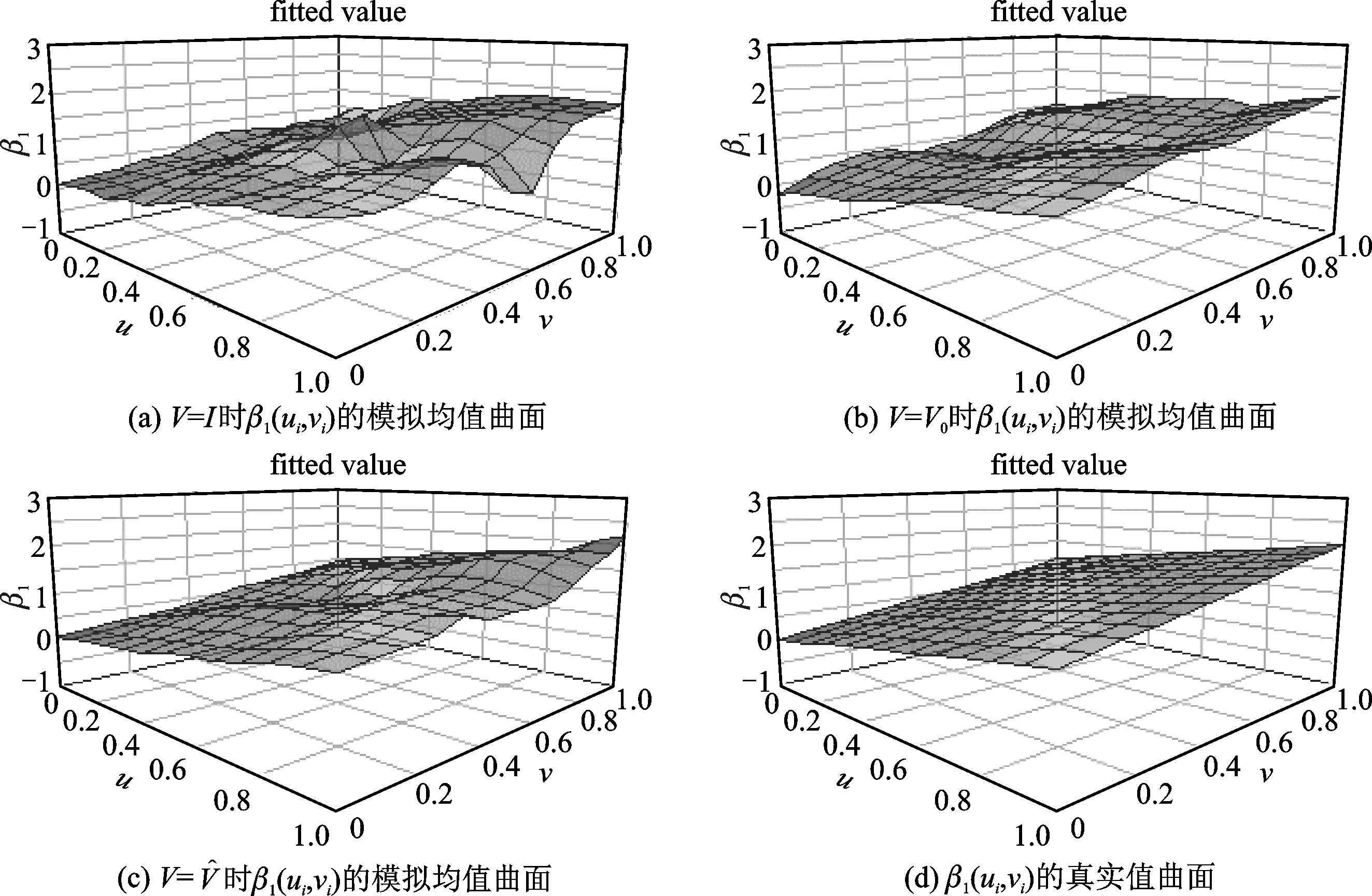
图3 n=169时,模拟均值曲面和真实值曲面

3.n=400时

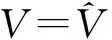
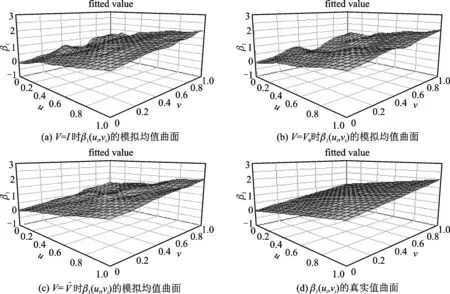
图4 n=400时,模拟均值曲面和真实值曲面

(四)不同方法下估计效果对比

现将空间变系数地理加权自回归模型的局部GMM方法下的参数估计效果和式(2)中的地理加权回归模型以及式(1)中的空间自回归模型下的估计效果进行对比,取样本量n=169。选择因变量Y模拟r次的均方根误差(RMSE)作为评价指标。

(21)

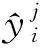
分别进行以下三组对比:

1.按照空间变系数地理加权自回归模型形式生成数据

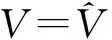
表2 模型估计情况对比

2.按照地理加权回归模型形式生成数据

数据生成过程的具体设计如下:(1)自变量:xi1～N(5,12),xi2～N(1,42);(2)残差向量:εi～N(0,0.252);(3)变系数:

β1(ui,vi)=ui+vi,β2(ui,vi)=3cos(πui)。由表3可以看出,若真实模型为地理加权回归模型,按照空间变系数地理加权自回归模型的局部GMM方法进行参数估计也能得到很好的结果。

表3 模型估计情况对比

3.按照空间自回归模型形式生成数据

(1)自变量:xi1～N(5,12),xi2～N(1,42);(2)残差向量:εi～N(0,0.252);(3)变系数:ρ=0.75,β1=-2,β2=3。由表4可以看出,若真实模型为空间自回归模型,按照空间变系数地理加权自回归模型的局部GMM方法进行参数估计能提高估计精度。综上所述,本文所提出的模型包含了常见的空间自回归模型和地理加权回归模型,针对实际数据进行分析具有广泛的适应性,不容易出现模型设定错误。当然,实际数据分析中,空间滞后回归参数和回归系数是否随着空间位置发生显著变化需要通过假设检验来检验,本文由于篇幅有限,不再讨论。

表4 模型估计情况对比

四、实证研究

收入和消费之间关系的研究一直受到广泛的关注,马骊等曾进行了城镇居民消费与收入关系的空间自回归分析[20]。本节将在考虑地理位置的基础上,利用本文提出的空间变系数地理加权自回归模型展开研究。模型设为:

(22)

自变量x为标准化处理后的2020年各地区城镇居民人均可支配收入,因变量y为2020年各地区城镇居民人均消费支出,数据来源于《中国统计年鉴2021》。工具变量的选取如上文所述。为了消除量纲的影响,将观测点的位置坐标(经、纬度)进行归一化处理,记为u、v。

原始数据如表5和表6所示,可以看出,东部地区的城镇居民人均消费支出和人均可支配收入总体较高。

表5 原数据——各地区城镇居民人均消费支出基本情况 单位:万元

表6 原数据——各地区城镇居民人均可支配收入基本情况 单位:万元

具体来看,城镇居民人均消费支出和人均可支配收入排名前六位的地区包括上海、北京、浙江、广东、天津、江苏(排名不分先后),这六个地区均属于东部地区。

关于空间邻接矩阵的设置,以地理上的接壤作为判定邻近的标准,由此得到邻接矩阵(这里认为海南和广东邻近),对邻接矩阵进行了行标准化处理,即得到空间权重矩阵W。

计算自变量和因变量的Moran’I指数,得到对应的P值均小于0.001,因此认为其空间相关性均显著。下面将空间变系数地理加权自回归模型的局部GMM估计的参数估计效果和式(1)中的空间自回归模型(SAR)下的估计效果进行对比。在后续模型分析中,如不特别说明,提到的城镇居民人均可支配收入(自变量)以及城镇居民人均消费支出(因变量)均为标准化后的数据。需要注意的是,在进行空间变系数地理加权自回归模型的局部GMM估计时,参考Malikov和Sun等的做法,选择平滑参数h1=h2=n-1/6[17]。

根据表7可知,纳入地理位置信息后,通过局部GMM方法估计后得到的因变量的均方误差比直接对空间自回归模型进行估计得到的均方误差要小,并且局部GMM方法估计得到的因变量的最小值、中位数、最大值和真实值的差距也更小。空间变系数地理加权自回归模型的局部GMM估计有效提高了估计精度。

表7 模型估计情况

由图5可以看到,个别观测点预测值和真实值间存在一定差距,但空间变系数地理加权自回归模型的局部GMM估计下预测值和真实值间差距整体更小,大多数预测值在真实值附近。空间变系数地理加权自回归模型的局部GMM下各ρ(ui,vi)和β(ui,vi)的估计情况如图6所示。x、y轴分别表示u、v的取值,z轴表示对应的系数函数变化值。可以发现,各变系数与变元(u,v)有关。ρ(ui,vi)的估计值大多为正,即某一地区的城镇居民消费支出大多受周边地区正面影响;β(ui,vi)的估计值基本为正,意味着城镇居民人均可支配收入对消费支出有显著的正面影响。

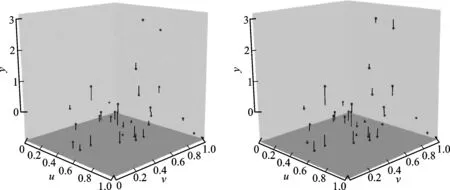
图5 因变量预测值和真值对比注:·真值(黑色大点)·预测值(灰点小点)误差线段。左图局部右图表示SAR。

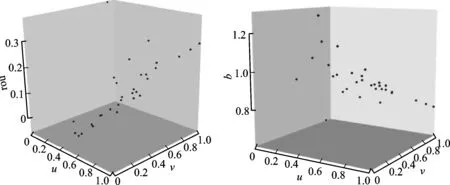
图6 变系数三维散点图

结合表8和表9,观察变系数ρ(ui,vi)的估计情况可以发现,全国31个省份的人均消费支出存在空间变化。ρ(ui,vi)的估计值在-0.057～0.382之间,除了广西、云南、西藏,其余多数地区的城镇人均消费支出受到邻近地区城镇居民人均消费支出的正向影响,消费水平高的地区会拉动周围地区的消费水平。在不同地区,ρ(ui,vi)估计值存在一定差异性,这表明城镇人均消费支出受周围地区的影响程度并不完全相同,存在空间异质性。

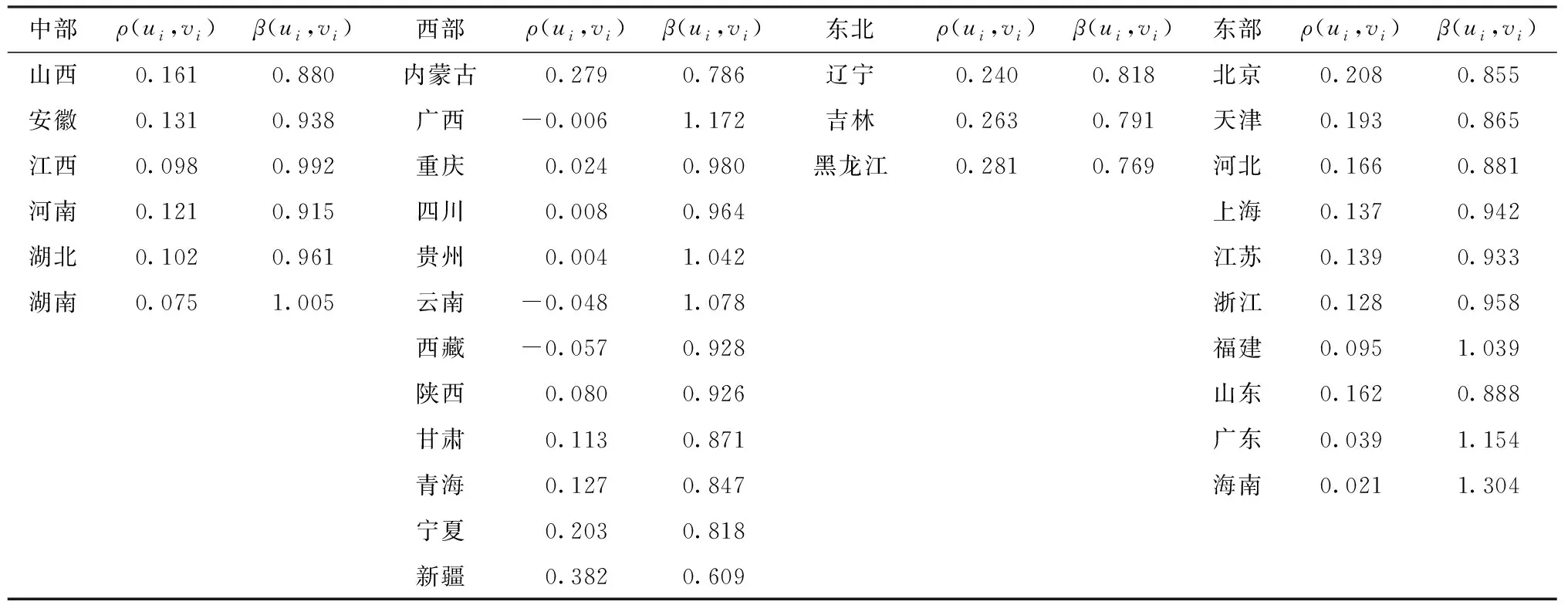
表8 各区域估计结果

表9 变系数估计情况

观察变系数β(ui,vi)的估计情况可以发现,全国31个省份的城镇居民人均可支配收入对人均消费支出总体呈正向的影响,总体来看,人均可支配收入高的地区消费水平更高。同样地,在不同地区β(ui,vi)估计值存在一定差异性,城镇居民人均可支配收入对人均消费支出的影响程度因地区而异。

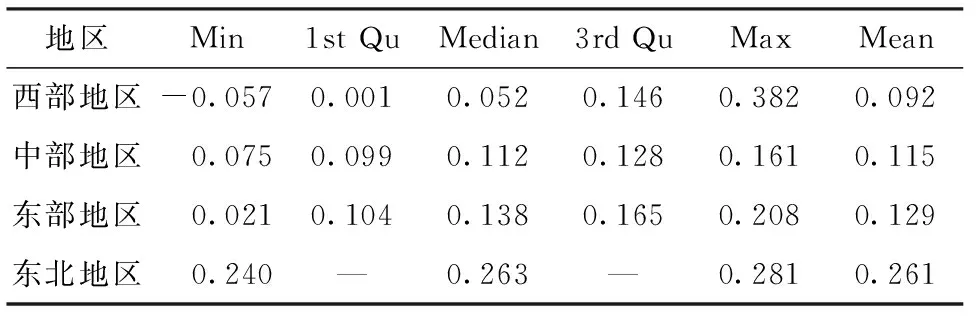
表10 ρ(ui,vi)分区域估计情况

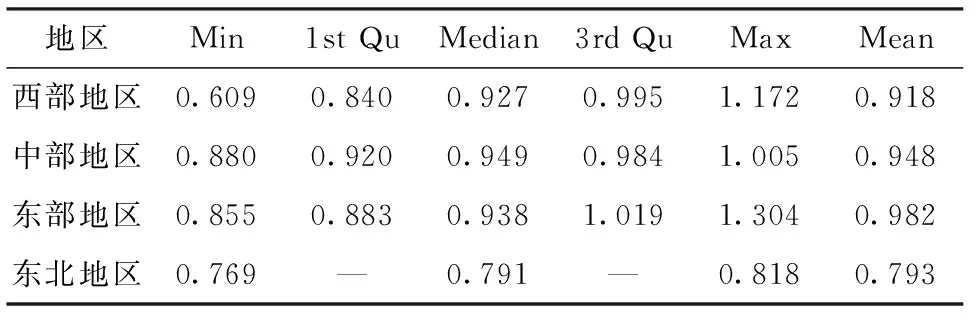
表11 β(ui,vi)分区域估计情况

分区域观察变系数ρ(ui,vi)的估计情况(见表10)。总体来说,东北地区城镇居民人均消费支出受邻近城市的影响程度更大。分区域观察变系数β(ui,vi)的估计情况(见表11)。总体来说,相比西部地区和东北地区,中部地区、东部地区城镇居民人均可支配收入对消费支出产生的影响更大。大多数位于东部地区的城镇居民人均可支配收入和消费支出均处于全国较为领先的地位,其对应的β(ui,vi)估计值较大,可以合理推测,城镇人均可支配收入较高的地区,可支配收入对当地消费支出存在的正面影响程度也可能较高。

五、总 结

为了能够同时刻画空间自相关性和空间异质性,本文研究了一类空间变系数地理加权自回归模型,该模型是经典空间自回归模型和地理加权回归模型的推广。基于局部线性技术和局部GMM方法,构造了模型中未知系数函数的估计量,通过数值模拟和实例考察了所提方法的有效性。实证研究了2020年城镇居民人均消费与收入关系,得到以下结论:一个地区的城镇居民人均消费支出大多受到邻近地区居民消费支出的正向影响,消费水平高的城市也会拉动周围城市的消费水平;城镇居民人均可支配收入对人均消费支出总体呈正向的影响,总体来看,人均可支配收入高的地区消费水平更高;城镇人均可支配收入较高的地区,可支配收入对当地消费支出存在的正面影响程度也可能较高。

本文重点研究了模型的局部GMM估计问题,如果对模型采用其他方法进行估计,比如采用工具变量两阶段最小二乘估计或者局部极大似然估计方法,都是值得探讨的问题。此外本文没有对所提估计量的理论进行深入研究。对于在实际数据分析中非常重要的检验问题没有涉及,比如空间滞后参数与回归系数是否为常数,空间自相关性是否存在等检验,这都是需要进一步研究的内容。