基于有限元的双道金属O形环压紧力分析*

刘长海 赵 栋 魏 雪 张 强

(东北石油大学机械科学与工程学院 黑龙江大庆 163318)

反应堆中的压力容器是核电站中非常关键的设备，其密封性能决定着整个核电站的服役年限，一旦密封失效将导致严重的核泄漏事故[1]。出于安全的考虑，反应堆的压力容器通常采用双道金属O形环的密封结构[2-4]，但针对双道密封结构的压紧力问题研究较少，因此需要开展对双道密封压紧力分析研究。

金属O形环是反应堆压力容器中常用的密封元件[5]之一。沈明学等[6]建立了二维轴对称的非线性有限元模型，分析沟槽尺寸参数对其金属O形环密封性能的影响。蔡永梅等[7]利用ANSYS建立了非线性有限元模型，并分析金属空心O形环在安装和使用时压缩率、回弹量及变形量随接触应力的变化规律。励行根等[8]成功研制出国产金属O形环并已投入生产使用。吴国凤[9]、赵丽娜[10]采用实验与模拟结合的方法对材料为Inconel718的金属O形环密封性能进行了分析研究。薛国宏等[11]利用ABAQUS有限元软件研究国产O形密封环在不同压缩率下的变形、应力并分析回弹量的影响因素。贺寅彪等[12]利用MSC.Marc软件对双道金属O形环进行弹塑性大应变接触分析，得到不同压缩量下O形环的回弹量。郭飞等人[13]在理想圆度金属O形环截面研究的基础上，分析出椭圆金属O形环关键截面特征点的运动轨迹，以及装配预紧过程的变形特征。张文昌等[14]采用有限元方法建立了O形环的仿真模型，分析了密封环的压缩回弹特性、应力应变特征以及接触特性。整理文献发现，学者们对于金属O形环密封性能研究的成果已有不少，但关于金属O形环压紧力的相关研究较少。GB 150《压力容器》[15]中仅给出了单道预紧状态下所需最小压紧力的计算公式，对于双道密封的总压紧力值的具体计算公式并无说明。

因此，本文作者在GB 150《压力容器》的基础上，利用ANSYS有限元软件，计算单道与双道密封的金属O形环压紧力，并对比理论计算值，开展对单道、双道密封最小压紧力计算公式的研究。

1 单道密封最小压紧力计算公式

在GB 150《压力容器》[15]中定义预紧状态下的最小压紧力为

Fa=3.14DGby

(1)

式中：DG为密封环压紧力中心圆直径，mm；b为有效密封宽度，mm；y为比压力，取179.3 MPa。

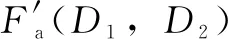
(2)

(3)

式中：A为第一道密封压紧力修正系数；B为第二道密封压紧力修正系数；C为总压紧力修正系数；D1、D2为第一、二道密封圈中心圆半径，mm。

2 金属O形环有限元模型

2.1 模型参数

金属O形环材料为Inconel718合金，法兰材料为P91。采用理想弹塑性模型，截面直径d=15.4 mm，厚度t=1.35 mm，间隙δ=0.6 mm，几何模型如图1所示。通常反应堆的金属O形环外表镀银是为了弥补密封面上的缺陷以提高密封性能，但已有研究表明有无镀银对有限元结果无明显影响[6]，所以，在接下来的分析中不考虑银层。

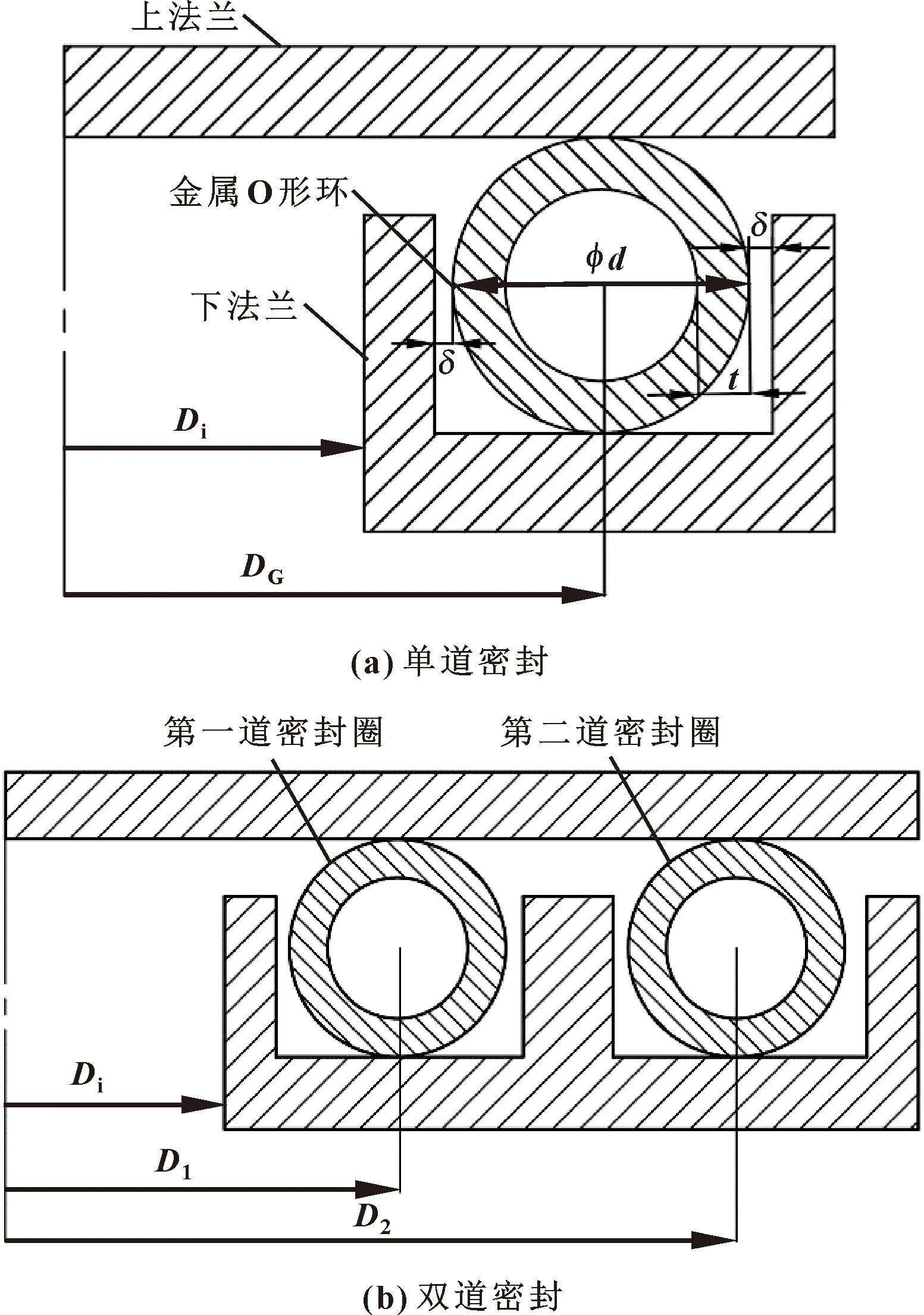
图1 O形环几何模型

为了探究在不同外径下O形环所受压紧力的变化规律，建立了单道与双道密封的有限元模型，建立模型的密封圈中心圆直径参数如表1所示，其中，单道密封环中心圆直径与双道密封中第一道密封环中心圆直径相等(DG=D1)，金属O形环与法兰的力学性能如表2所示[16]。

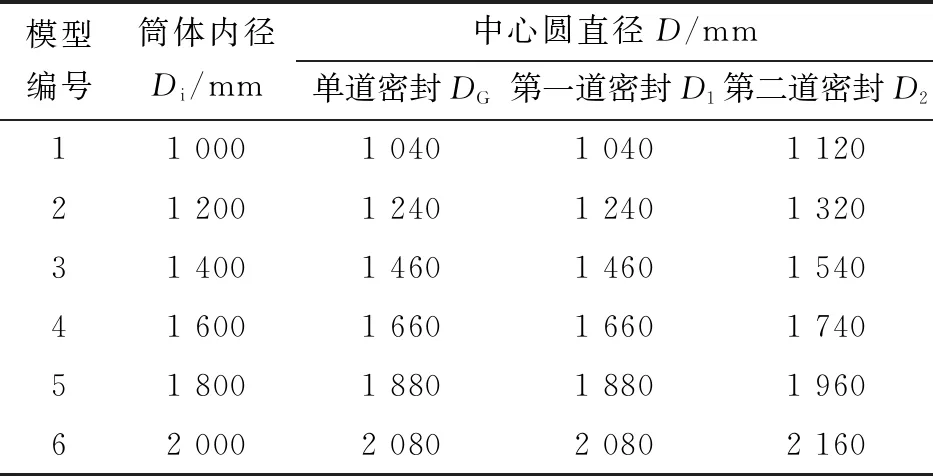
表1 模型参数

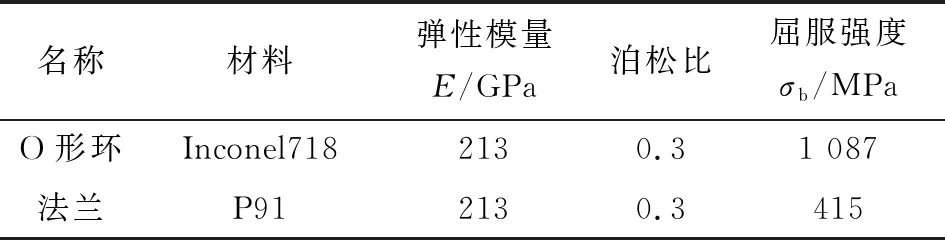
表2 材料力学性能

2.2 边界条件

由于密封结构的特殊性，采用的是二维轴对称的PLANE183单元进行各部分的网格划分，如图2所示，二维面面接触单元为CONTAC172，目标单元为TRAGE169，接触单元与目标单元之间构成接触对。

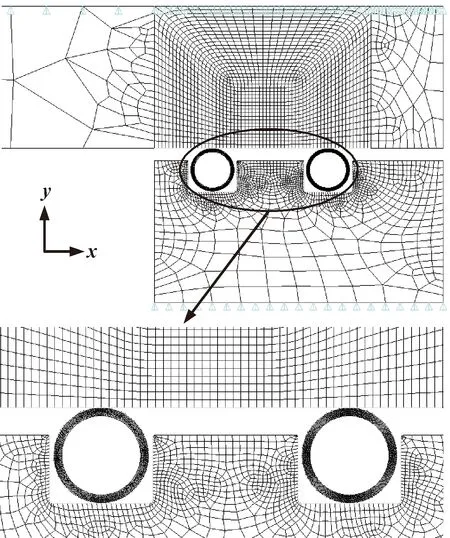
图2 O形环网格划分

对O形环边缘以及法兰接触边缘进行网格局部加密划分，以提高计算精度。金属O形环与法兰接触摩擦因数取0.15[2,16]。将O形环压紧过程处理成大变形问题，O形环分别与上法兰、沟槽建立接触对，共计2对接触对。下法兰边界约束y方向位移，上法兰沿y轴施加负向位移。

3 结果与讨论

利用有限元求解的压紧力计算公式为

(4)

式中：Ai为上法兰与O形环的第i个单元接触面积，mm2；pi为上法兰与O形环的第i个单元接触压力，MPa；N为接触单元总个数；F为O形环所受压紧力，N。

有限元计算的单、双道各密封圈压紧力值与理论计算值如表3和表4所示。由表3和表4可知，当压缩率取9.7%时，此时上法兰沿y轴负向施加位移为1.500 75 mm，有限元计算的压紧力就已大于理论计算值，且有限元的计算结果与理论值的误差小于1%。可以认为，在该压缩率下，单道密封和双道密封O形环就已达到了预紧状态下的最小压紧力。

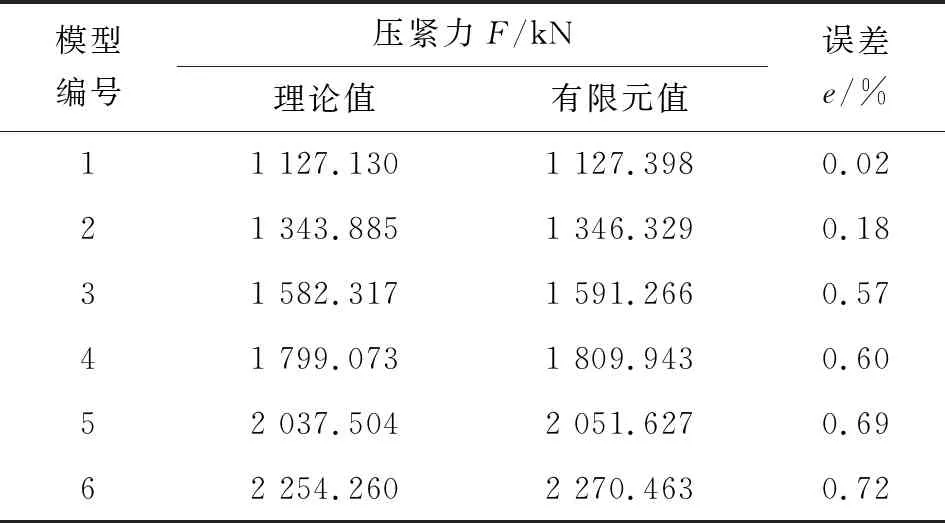
表3 压缩率为9.7%时单道密封环所受压紧力

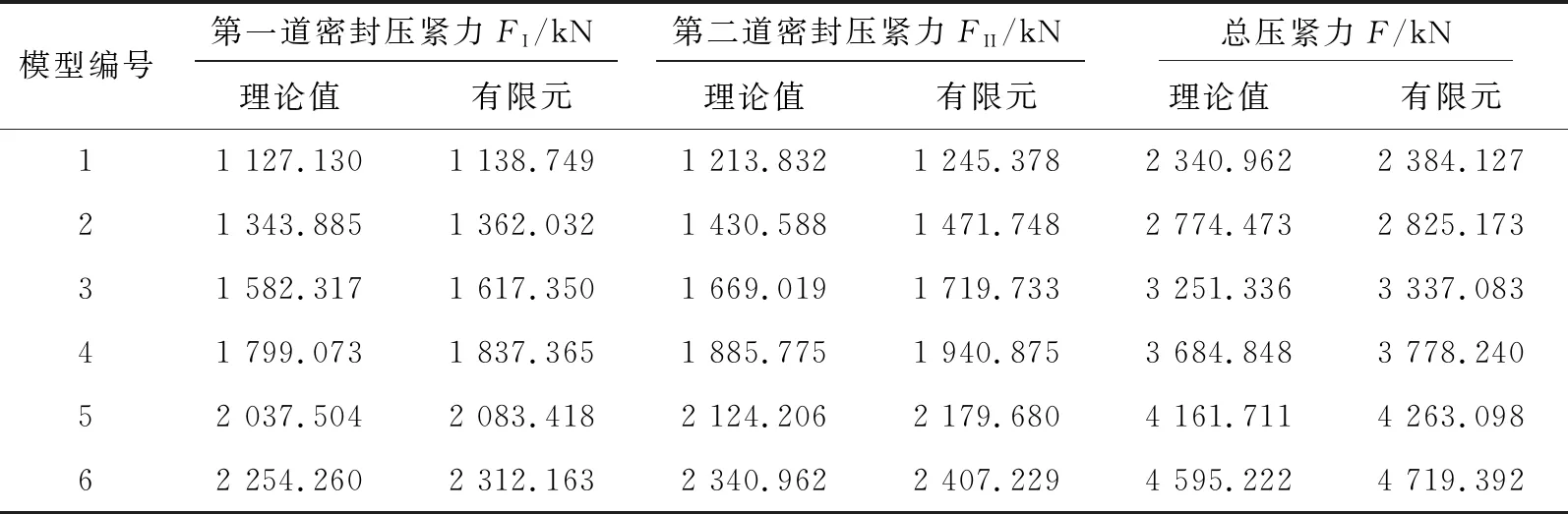
表4 压缩率为9.7%时双道密封O形环所受压紧力

图3给出压缩率为9.7%时单道密封与双道密封的第一道密封环压紧力对比关系(DG=D1)。可知，随着筒体内径的增大，密封圈的中心圆直径相应增大，密封圈所需的压紧力也越来越大。在模型1—6中，虽然密封环的中心圆直径相等，但双道密封的第一道密封环最终的压紧力始终大于单道密封，这是由于双道密封中存在两道密封，因此在预紧时密封环所需的压紧力也会相应增加。

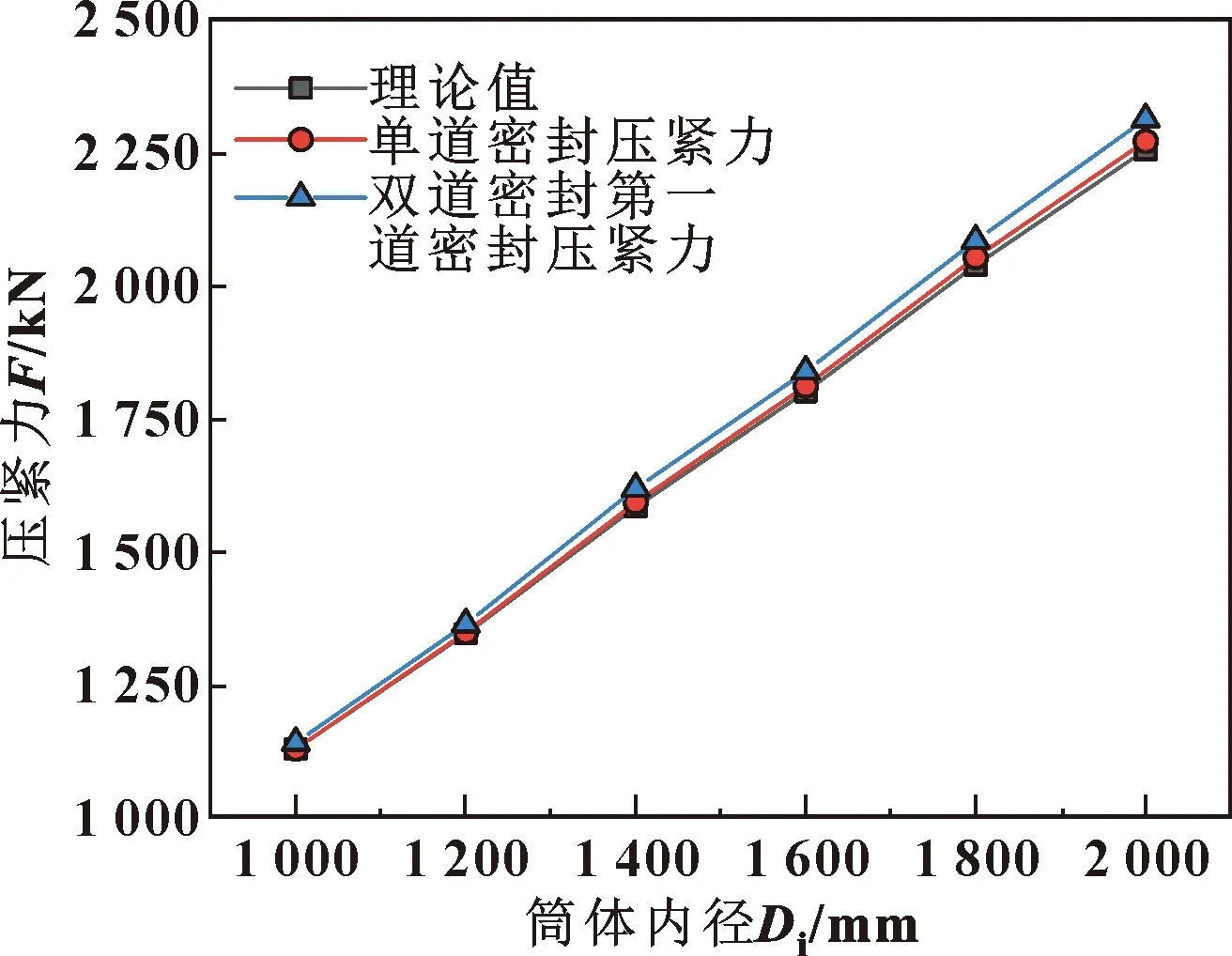
图3 单道密封与双道密封的第一道密封环压紧力随筒体内径的变化

图4所示为模型1在压缩率λ为5%、7.5%和9.7%时x和y方向的变形云图。由图4(a)、(b)可知，双道密封环在压缩率λ为5%、7.5%和9.7%时x方向的最大位移分别为0.32、0.47和0.62 mm，y方向的最大位移分别为0.79、1.16和1.53 mm，说明当压缩率为9.7%时密封圈两端已跟沟槽接触。由图5可知，在压缩率为9.7%时，最大Mises应力位置发生在O形环与法兰和沟槽的接触端外侧，以及接触端向内凹陷处，且均已达到屈服极限，发生了塑性变形。

图4 模型1在压缩率为5%、7.5%、9.7%时的变形云图

图5 模型1在不同压缩率下的Mises应力云图

4 双道密封压紧力的公式修正

如图6所示，随着压缩量增大至1.54 mm时(压缩率10%)，O形环所受压紧力呈现先增大后减小再增大的无规律变化，单道和双道密封的压紧力曲线变化趋势相同；当压缩量由1.54 mm增至3.08 mm(压缩率20%)，双道密封总压紧力曲线先是急剧增长，当压缩量达到1.81 mm时，曲线呈波动式缓慢增长；当压缩量为1.84 mm时，单道密封压紧力曲线也开始呈波动式缓慢增长。

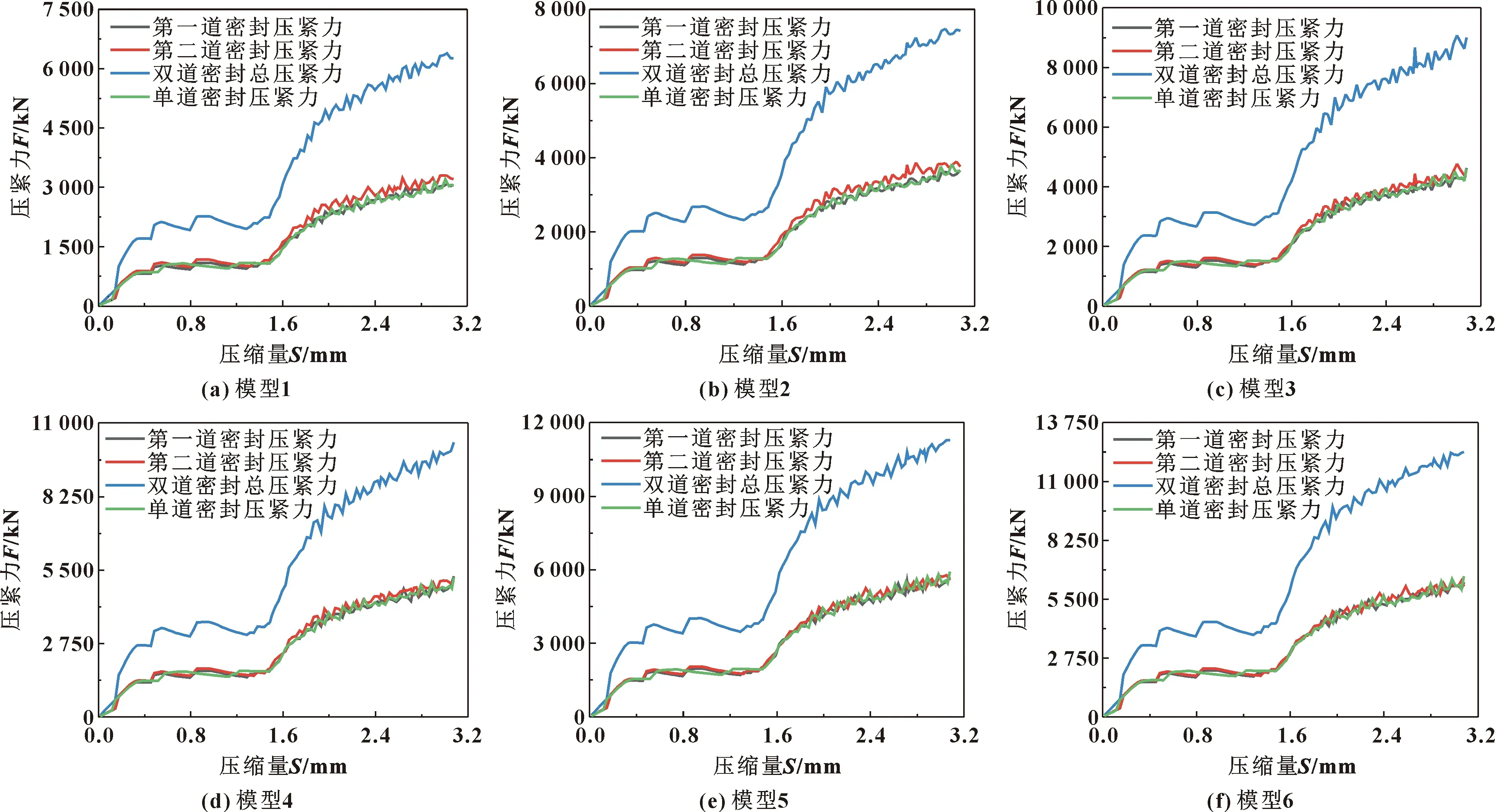
图6 模型1—6压紧力和压缩量关系

根据表4中的双道密封压紧力值，将表中每道密封及总的压紧力有限元值与理论值相除，分别得到相应的修正系数A、B、C后取均值，得到修正系数A=1.021，B=1.028，C=1.024。将修正系数分别代入修正公式(2)和(3)中，得到

F1=1.021×3.14D1by+1.028×3.14D2by

(5)

F2=1.024×3.14(D1+D2)by

(6)

由修正公式计算得到最小压紧力值与有限元值、理论值的对比如图7所示。可知，F1和F2计算值和有限元计算出的最小压紧力值基本一致，但结合表5中F1和F2计算值及与有限元的误差值来看，F1计算值与有限元结果的误差最小。因此，F1所计算的数据较F2更加符合有限元计算值，综上，选择式(5)为最小压紧力的最终修正公式。

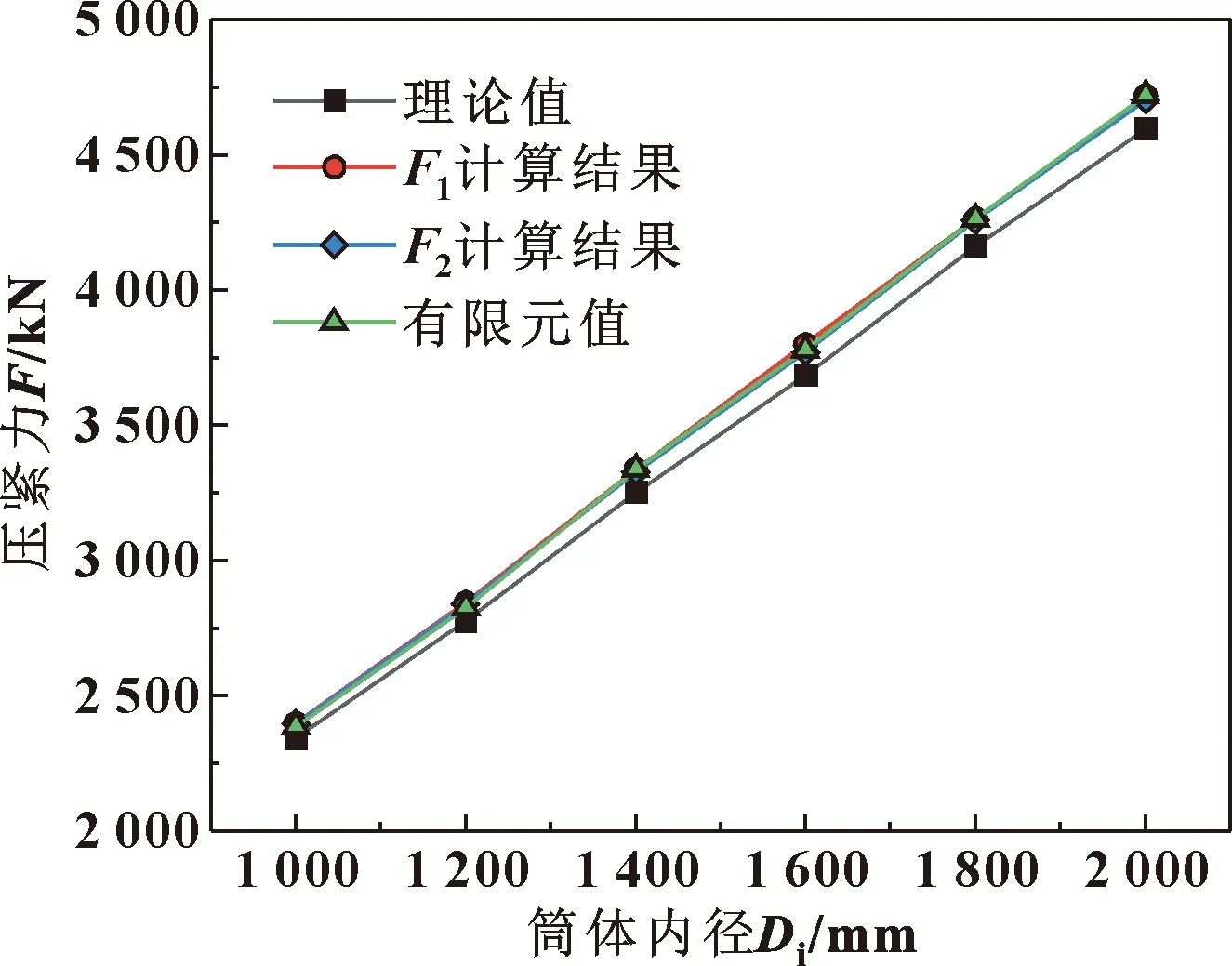
图7 修正公式计算的F1、F2与有限元值和理论值对比

表5 修正公式计算的F1、F2与有限元计算值对比

5 结论

(1)通过分析单道和双道密封模型的计算结果可知，密封圈中心圆直径一定，在相同压缩率9.7%下，单道密封压紧力值小于双道密封的第一道密封圈压紧力。在整个压缩过程中，双道密封与单道密封的压紧力曲线变化趋势相同。在实际工程应用中，建议取压缩量大于1.5 mm，以达到预紧状态下的最小压紧力。

(2)当金属O形环外径一定，压缩率为0～10%，单道和双道的O形环所受压紧力均呈先增大后减小再增大的变化规律；当压缩率为10%～20%，单道和双道压紧力曲线开始呈波动式缓慢增长。

(3)修正后的压紧力公式结果与有限元值具有良好的一致性，可用于双道密封下金属O形环所需最小压紧力的计算。