拓扑切换和时延下的非线性多智能体协同输出调节

尉晶波， 魏文军

(兰州交通大学，兰州 730000)

0 引言

协同输出调节[1]是指设计一个控制器，在外部系统作用下，多智能体系统实现对外部系统信号的渐近跟踪和干扰抑制。多智能体系统的协同输出调节有着广泛应用，如编队控制[2-3]、移动机器人路径跟踪[4]和航天器编队飞行[5]等。在实际系统中，通信速度有限，导致通信产生时延[6]。通信拓扑变化和时延是影响多智能体系统稳定性的两个重要因素，大量文献研究了拓扑变化和通信时延对多智能体系统稳定性的影响。

文献[7-8]解决了拓扑切换和时延下的线性多智能体协同输出调节问题；文献[9-11]主要研究了在固定拓扑和联合连通拓扑切换下线性定常系统的领导跟随一致性问题，但所提方法无法满足时变系统，有一定的局限性；文献[12]提出了基于状态反馈和输出反馈的事件触发控制律算法，解决了拓扑切换下异构多智能体协同输出调节问题；文献[13]为解决线性多智能体状态不可测的协同输出调节问题，提出了通过设计自适应分布式观测器获取智能体状态信息来解决协同输出调节问题。上述文献主要研究了线性多智能体系统的协同输出调节问题。然而，由于实际系统主要以非线性系统的形式出现，因此，解决非线性多智能体系统的协同输出调节问题是非常重要的。

文献[14-15]研究了联合连通拓扑切换下非线性多智能体协同输出调节问题，提出了分布式模糊输出反馈控制器，解决了多智能体状态不可测条件下的系统协同输出调节问题；文献[16]研究了二阶非线性多智能体通信时延一致性问题，提出了一种仅基于相对位置的分布式一致性协议，但有一定的局限性；文献[17-20]提出的T-S模糊模型通过线性局部子系统对非线性系统有很好的近似，不仅有效地描述非线性系统的行为，也展现了线性系统的性质。到目前为止，研究拓扑切换和时延下的非线性多智能体协同输出调节问题的文献仍较少，尤其是当智能体无法获取外部系统状态信息情形下的协同输出调节问题。

基于上述分析，为解决切换拓扑和时延下非线性多智能体无法获取外部系统状态信息的协同输出调节问题，本文提出了分布式状态观测器控制算法和模糊反馈控制策略。

1 图论

H=D-A

(1)

式中，H=[hi j]∈RN×N，

(2)

存在一个可逆矩阵T，使得T-1HT=Λ=diag(0,λ2,…,λN-1,λN)成立。其中，0<λ2≤…≤λN为矩阵H的特征值。

2 多智能体系统描述

智能体i和外部领导者的动态方程为

(3)

(4)

式中：xi为智能体i的状态向量；ui为控制器；ei为智能体i的系统误差；Am,Cm,v0,y0分别为外部系统的状态矩阵、输出矩阵、状态量和输出,Am∈Rn×n,Cm∈Rn×n。

通过模糊隶属度函数将不同模糊规则下的线性子系统光滑连接逼近非线性系统。模糊规则如下。

(5)

式中:Ai l∈Rn×n，为线性子系统的状态矩阵；Bi l∈Rn×1，为控制矩阵；Ci l∈Rn×n，为误差线性子系统的输出矩阵；Di l∈Rn×1,为前馈矩阵;xi∈Rn×1；ui∈R1×1；v0∈Rn×1；Ei l∈Rn×n；Fi l∈Rn×n;l=1,2,…,r,r为模糊规则数。因此，非线性系统在模糊规则下描述为如下线性系统

(6)

其中，隶属度函数

(7)

(8)

在模糊规则下，式(6)可简写为

(9)

在本文中，切换拓扑用gσ(t)表示。推导本文结论前，假设非线性系统满足以下假设和定义。

假设1 (Ai l,Bi l)是可控的。

假设2 (Ai l,Ci l)是可观的。

假设3 矩阵Am特征值均具有非负实部。

定义1对于非线性多智能体系统，假设通信拓扑为有向的。设计控制器ui满足如下条件。

条件1 当v0(t)=0时，式(11)闭环系统渐近稳定。

则设计的控制器ui能够解决系统的协同输出调节问题。

3 拓扑切换时延控制律设计

为解决拓扑切换和时延下的多智能体协同输出调节问题，本文设计了模糊反馈控制器

ui=K1ixi+K2iξi

(10)

和分布式状态观测器拓扑切换时延控制律

(11)

(12)

定理1若满足假设3，对于给定正定对(Am,Cm)，存在正定对称阵P满足Riccati方程式

(13)

(14)

构造Lyapunov-Krasovskii方程

(15)

对V(t)进行求导并应用引理1和定义1可得

(16)

(17)

有唯一解(Xi,Ui)。

(18)

(19)

式(12)闭环系统可写为

(20)

(21)

(22)

(23)

同理，非线性多智能体误差方程可以写成

(24)

(25)

4 仿真算例

非线性系统由4个智能体和1个外部领导者组成。系统切换有向通信拓扑如图1所示。

图1 切换拓扑

图中：0表示外部领导者系统；1,2,3,4表示多智能体。拓扑切换顺序为S1→S2→S3→S4→S1。

各智能体的非线性动态方程为

(26)

外部领导者动态方程为

(27)

用T-S模糊理论将系统的非线性方程式(26)转化为线性方程。其T-S模糊规则如下。

(28)

(29)

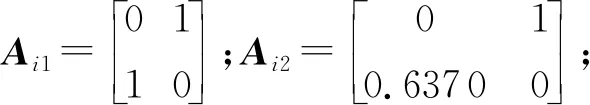
模糊规则l对应的隶属度函数为

(30)

绘制在式(10)、式(11)控制律作用下的非线性智能体各状态图和误差图。

1) 时延参数τ=0 s时，控制律作用下的结果如图2所示。

图2 τ=0 s时控制律作用下系统误差和系统输出

2) 时延参数τ≠0 s时，控制律作用下的结果如图3所示。

图3 τ≠0 s时控制律作用下系统误差

对比图3(a)～3(c)可知，非线性多智能体系统在不同时延参数下达到稳定的时间不同。由图2(a)可知，当时延参数τ=0 s时，多智能体大约在第10 s跟踪到外部领导者。由图3(b)可知，当时延参数τ=0.5 s时，多智能体在第16 s左右跟踪到外部领导者，误差为零。由图3(c)可知，当时延参数τ=0.785 s≥τmax时，非线性多智能体跟随者不能跟踪到外部领导者信号，系统无法达到稳定。

5 结束语

本文研究了拓扑切换和时延条件下的非线性多智能体协同输出调节问题。为使状态不可测情况下跟随者能够跟踪到外部领导者系统，设计了式(10)模糊反馈控制器和式(11)分布式时延状态观测器控制律，并用Lyapunov稳定性理论证明了系统的稳定性。仿真结果表明：多智能体跟随到外部领导者系统所需的时间与时延参数τ有关。时延参数τ越大，系统达到稳定所需时间越长；当时延参数τ大于时延上限值时，非线性多智能体系统最终无法达到稳定。