基于MATLAB的Canny图像边缘检测优化与实现

2022-11-03蔺玉珂杨敏贺中屏曹华王家麒

现代信息科技 2022年17期

蔺玉珂，杨敏，贺中屏，曹华，王家麒

（重庆电子工程职业学院，重庆 401331）

0 引言

图像识别是计算机对图像进行处理、分析和提取信息，并识别到不同模式不同目标或物体的技术，对质量较差的图像也可以进行一系列增强和重建，能够有效提高图像质量。图像识别的第一步往往是边缘识别，即一个区域的结束和另一个新区域的开始，反映图像特征的不连续性。

19世纪60年代初至80年代末，图像边缘识别理论正处于发展的黄金时期。20世纪70年代初，Prewitt 和Kirsch开始研究定向边缘识别技术。1977年Robinson 还对 Prewitt和 Kirsch 的相关研究成果进行了总结和概括。在1980年，Marr 提出了LoG 算法，可以通过引入高斯滤波器来降低对噪声的影响。1986年，伟大的美国算法物理学家John Canny，提出了后来被称为Canny 原则的边缘识别三原则。

吕哲提出了一个经过改进的Canny 算法，主要改变了梯度方向检测方式和连通性。对于高环境光和低强度边缘的定向测量，能够有效地抑制在高环境光影响下的峰值信噪比，同时边缘细节也被保持，但高自动调节的阈值会对边缘细节测量结果产生一定的负面影响。因此，罗涛通过对高、低阈值的选取，并提供了一个更完善的高自适应阈值Canny测量算法，克服了人为因素引起的测量边缘损坏和边缘误差的问题，但在彩色画面检测和试验的过程中，仍有部分受损的边缘存在。Deng对传统的Sobel 算子进行了改进，为图像的开闭运算引入Sobel 算法，然后分别使用改进的小波变换算法、Sobel 算法、Canny 算法和Prewitt 算法对图像边缘进行识别。最后，根据定义的图像融合算法，对各种方法得到的图像边缘进行融合，得到最终的识别结果，使得边缘提取结果完整，定位精度高。

图像边缘是图像最基本也是最重要的特征，提高图像识别率主要有两种方式：一是提高硬件的识别率，二是提高软件的识别率。目前提高硬件识别率存在许多困难，而后者利用现有技术可以解决，所以从软件上来提高识别率的意义较大。

目前，实现图像边缘识别的软件和算法有很多，但学者们仍在寻找更通用、更高效的边缘识别算法。其中最具代表性的四种检测算法分别是基于形态学的、基于小波变换和小波包的、基于模糊理论的，以及基于分形几何的边缘识别算法。

除上述算法外，还有一些边缘识别算子的经典方法，如Roberts 算子和Sobel 算子、Canny 算子等。Canny 算子利用寻找（，）上的梯度的局部最大值来找到强边缘，梯度强度也可以由高斯滤波器的微分来估计，使用两个阈值识别到强边缘和弱边缘，并且假设它们都被连接到强边缘，这样就在输出中只包括弱边缘。

1 图像处理设计步骤

在获取原始图像的数据区域指针后，需要经过灰度化、高斯滤波、像素梯度计算等一系列操作之后，最终得到边缘识别效果图。

1.1 灰度化

Canny 算法通常处理的图像往往都是灰度图像，而在实际应用中通常使用彩色画面，所以一般先进行灰度化，将彩色画面变成灰度图像。以RGB 格式的彩图为例，通常灰度化使用的公式是：

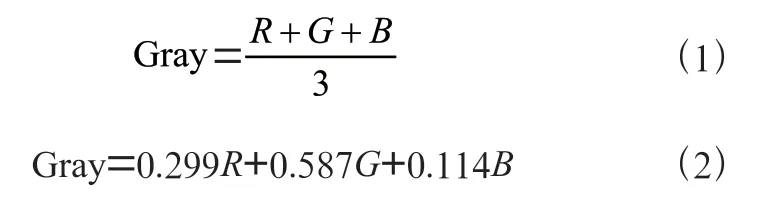
注意，在程序设计时一般按照图像格式中RGB的顺序，一般是BGR，但MATLAB 等软件支持把输入的彩色图像直接转换为灰度图像，因而可跳过这个操作。

1.2 高斯滤波去噪

任何边缘识别算法在未经处理的原始图片信号上都不能得到很好地处理效果，所以首先是对原始图片信息与高斯mask 做卷积，得到新的图像信息与原始图像形一样有很细微的模糊度（blurred）。这样一来，图像噪声在经过高斯平滑的图像上就基本没有影响。

对图像高斯滤波可以进行去噪，对图像高斯滤波的实现也可以用一维高斯核分别进行二次加权的运算实现，也就是先一维X向卷积运算，所得的结果再一维Y向卷积高斯滤波，使用的高斯核可以是有X 和Y 两维的高斯函数，且两个维度上标准差一般取相同，形式为：

一维高斯函数：

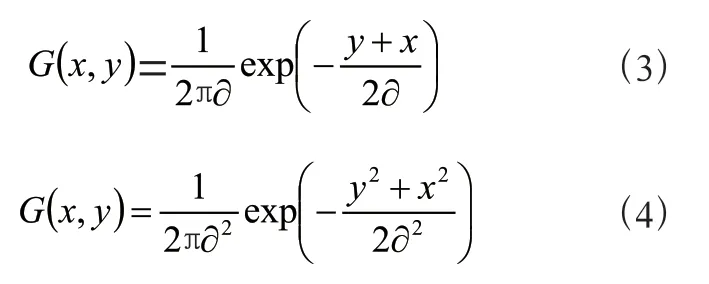
高斯滤波法，即是即通过在某一尺度上的二维高斯核，与像素进行卷积。因为数位影像的基本数据形式为离散矩阵，所以高斯核就是对连续高斯函数的离散化处理，可通过对高斯面体进行离散采样后的归一化而得出。所以，边长为3×3，其标准差为一的高斯核为：

在确定高斯核后，将其与图像进行离散卷积即可。利用高斯滤波器与图像进行卷积，以平滑图像，并消除噪音影响。高斯滤波器的核心位置为×（为奇数）。滤波器核心位为，高斯滤波器核的产生方式为：

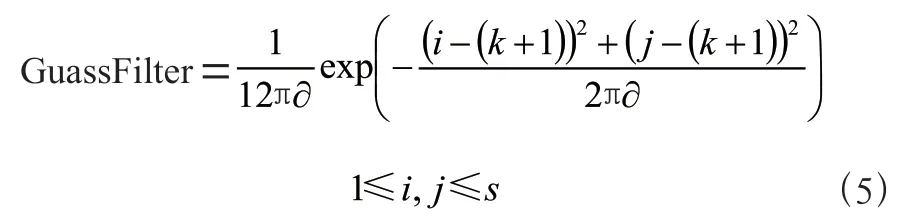
经过高斯去噪处理过的lena 图与原图对比，如图1所示。

图1 高斯去噪效果图

1.3 用一阶偏导的有限差分来计算梯度的幅值和方向

利用Sobel 算子的像素梯度，Sobel 算子中有两个3×3的矩阵，分别是S和S。前者用于计算图像方向像素梯度矩阵G，而后者则用于计算图像方向像素梯度矩阵的G。

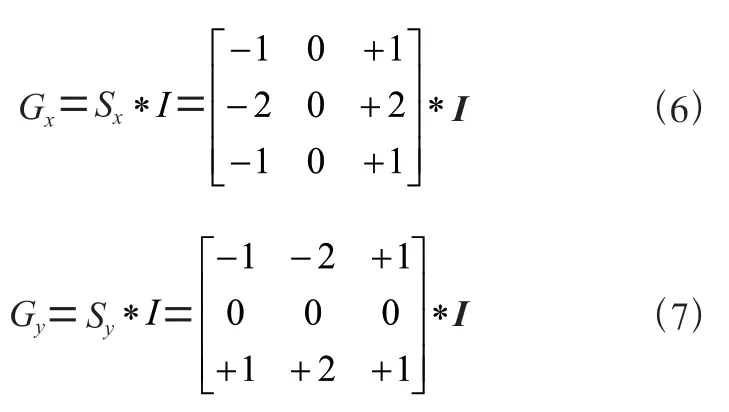
其中，为灰度图像矩阵，且此处的*表示互相关运算（卷积运算可视为将卷积核旋转180°后的互相关运算）。需要说明的是，图像矩阵坐标系原点在左上方，且正方向为从左往右，正方向为下往上。则由以下公式可计算得到梯度强度矩阵G（，）。

使用Sobel 算子的梯度处理lena 图，没有加阈值，效果如图2所示。

图2 Sobel 算子的梯度处理lena 图

1.4 对梯度幅值进行非极大值抑制

非极大值抑制是一个边缘的细化方法，通常可看作不只有一个像素宽度，而是多个像素长度的渐变边缘。正如我们所说，Sobel 算子的边缘通常既粗又亮，从图2中的Sobel 结果就可以知道。但是，梯度弥散图也是“模糊”的，所以在实际具体操作中，边缘通常只有一个很精确的节点之宽，而非极大值抑制可以保持局部的最大梯度值变化并抑制所有其他局部梯度值变化，这也就意味着只保护梯度变化中最尖端的地方。

若在当前点的梯度强度与相同方向上其他点的梯度强度相比最大，则保持在该值。否则，设置为零。如与当前点垂直上升约九十度，则必须在垂直方向上与其正上方和正下方的图像进行对比。

非最大像素梯度抑制的目的是消除边缘识别引起的杂散响应，即边缘被“细化”。基本办法是把当前像素点的梯度强度，和邻近像素点沿正梯度方向的梯度强度加以对比。如果是最大值（即极值），则保留在该像素的边缘位置；如果没有最大值，则会被抑制，不被视为边缘点。为了更精确的计算，通常在梯度方向上的两个相邻像素之间使用线性插值来获得待比较像素的梯度。

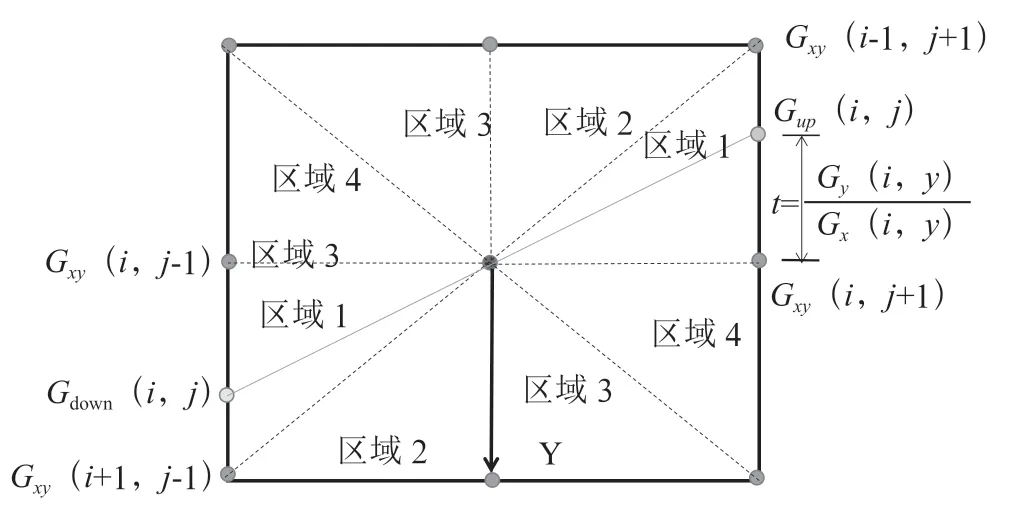
图3 像素梯度方向线性插值示意图

像素的邻接可分成四大区域，而每个区域都有左右两个部分。假设中心像素在向的梯度强度为（，），方向梯度强度为（，），梯度强度为G（，），则梯度方向所属的区域可以根据（，）或者（，）的正负和来确定。然后，根据其像素和其像素梯度方向与相邻点的像素梯度弥散值进行线性插值得出正负梯度方向的两个梯度强度（，）和（，）。

另外三个区域的计算方法相同，若G（，）=G（，）=0，说明像素点无像素梯度，则为非边缘。将梯度角离散化为圆的四个扇区之一，再使用3×3 窗口进行抑制操作，这些扇区标记为0 到3，对应于3×3 邻域有着四种可能组合。在每一点，将邻域的中心像素与沿梯度线的两个像素进行比较，如果的梯度不大于沿梯度线的两个相邻像素的梯度，则令（，）=0。非极大值处理结果如图4所示。

图4 非极大值抑制结果图

定义梯度强度的最高阈值与最低阈值，在梯度强度的最低阈值的像素点被抑制，因此也可以看成为边缘点，在最高阈值之下的每个像素点将被分类为强边缘，并保持为边缘点状态。而那些介于高阈值与低阈值之间的像素点则被认定为弱边缘，仍有待进一步处理。通过检测弱边缘图像及其8 个邻近图像，能够通过它和强边缘的联系来确定是否为真实边缘。一般可以定义，只要邻域图像之一为强边缘图像，就能够把弱边缘保留到强边缘点，即真实边缘点。

1.5 双阈值算法和连接边缘

目前减少“假边缘”数量最常用的方法是双阈值算法，对[，]使用一个阈值，为低于阈值的点分配为零，解决方法就是采用双阈值算法。双阈值算法对非最大值的抑制图像使用高低阈值MinVal 和MaxVal，若2 倍的MinVal 大约等于MaxVal，则即可获得两个阈值的边缘像素MaxVal[，]和MaxVal[，]。因为图像MaxVal[，]是利用较高的阈值而获得的，故包含的“假边缘”相对较小，但存在着不连续点（非封闭边缘）。双阈值方法将边缘和像素之间从MaxVal[，]中的轮廓连接起来，到达轮廓端点后，双阈值算法将MaxVal[，]的8 个相邻点与边缘轮廓连接起来，得到新边缘，在MinVal[，]内继续收集边缘，直到MaxVal[，]被完整连接。

2 实验结果与分析

在MATLAB 环境下对实现了基于Canny 算子的边缘检测，并与MATLAB 内置的Canny 边缘检测API 进行了对比实验，如图5所示，其中“Lena”为计算机视觉领域的常用测试图片。

图5 Canny 算子边缘识别处理Lena 图

为了达到更好的识别效果，在边缘识别程序中调整滤波器参数，在滞后阈值处理中调整高低阈值。MATLAB 的Canny 边缘识别API 使用其默认参数，推测的高低阈值可以通过自适应算法本身进行计算。从图5的识别效果可以看出，与API 相比，自己设计的Canny 识别程序提取了更多的详细信息，同时也保留了更多的局部噪声，API 提取的轮廓特征清晰，但局部失真严重。将默认的高斯半径修改为2，阈值保持不变，与原始图像对比如图6所示。从实验过程中可以看出，Canny 算子对滤波参数的选择和高低阈值的取值范围还是比较很敏感，在实际应用过程中需要反复调试。