复杂网络知识传播模型分析

梅俊，王思馨，夏丹，王维峰

（1中南民族大学 数学与统计学学院，武汉 430074；2华中师范大学 人工智能教育学院，武汉 430079）

知识传播在知识经济时代有重要的作用.知识传播为知识经济提供良好的氛围，并促进经济社会的发展和完善［1］.知识传播推动社会经济生产力的发展和进步［2］.并且，隐性知识及其传播可构成企业的核心竞争力［3］.另外，知识传播还能有助于抑制传染病的传播，例如宣传戴口罩可有效的抑制新冠病毒的传播［4］.因此，研究知识传播具有一定的实际意义.

由于复杂网络可以解释系统的运作方式［5］以及知识传播和传染病传播的相似性，有很多研究在复杂网络上建立类似于传染病传播模型的知识传播模型.例如，考虑将显性知识转变为隐性知识的内在化机制建立了一个Receivers-Holders-Spreaders（RHS）模型［6］；为了分析复习回顾机制，在复杂网络上建立了一个Naive-Evangelical-Agnostic（VEA）模型［7］；通过考虑自学机制提出了一个Susceptible-Infected（SI）模型［8］.在传染病模型中，基本再生数是决定病毒是否传播的标志，它是指在无病平衡状态中，一个传染病病人在平均染病周期内所感染的人数［9］.

在熟人社交网络平台上，用户转发分享的文章内容很有可能被好友再次转发分享［10］.熟人之间的相熟关系既可以降低知识接收者对知识的怀疑程度也可以使知识接收者和知识传播者及时分享反馈知识的难易程度、知识与人们生产生活的相关度以及知识接收者对知识的接受度等相关信息，这可以让知识传播者根据反馈及时调节传播内容和模式使其更容易被知识接收者接收，这也就是说熟人所分享的知识更容易被周围的知识接收者接收，更进一步说，熟人有利于知识传播.本文将熟人定义为知识接收者周围具有一定知识传播能力的人，例如父母、亲戚朋友、老师等.

在现有文献中，学者们只研究了友谊［11］以及领导者［12］在知识传播中的单一作用，对熟人的总体作用考虑较少.本文首次在复杂网络知识传播过程中考虑熟人作用并对其进行了建模和动态分析.首先，应用平均场方程建立了一个SIH模型，其中知识传播过程表现为个体的状态变化.其次，从理论上分析了SIH模型的动态性能，包括其基本再生数、平衡点及其稳定性.最后，我们通过数值仿真验证了理论分析结果并进一步研究模型参数对SIH模型的影响.

1 SIH模型

考虑到熟人作用，本文建立了一个基于传染病SIR模型的知识传播SIH模型.假设复杂网络是异构的并且个人可以自由进出.知识传播实际上是一种学习效应，即低知识水平的接收者可以从高知识水平的传播者中学到一定的知识［13］，但知识在人脑的存在时长是有限的.因此本文将人群分为三大类：知识接收者（S），知识传播者（I），知识遗忘者（H）.知识接收者（S）是指没有拥有特定知识信息的人，他们对知识都有极高的渴求性，他们愿意学习知识并且相信知识传播者所传播的知识.知识传播者（I）是指拥有特定知识信息的人，他们乐意分享传播自己的知识.知识遗忘者（H）是指随着时间的推移，知识传播者（I）逐渐遗忘知识的人，他们都是拥有过知识的人.

如图1所示，知识接收者在与熟人接触交流的过程中，熟人将知识传播给接收者，使得知识接收者成为知识传播者，这个概率为β1(0≤β1≤1).同时，知识接收者还可以自己从网络、书本等知识库中汲取知识成为知识传播者，这个概率为α(0≤α≤1).由于长时间未应用知识或者该知识被新的知识所覆盖，知识传播者将遗忘这种知识成为知识遗忘者，这个概率设为γ(0≤γ≤1).但当知识遗忘者处于周围都是知识传播者的环境下，知识遗忘者可以被拥有知识的熟人提醒或者再次传播，于是知识遗忘者就可以重新变为知识传播者，这个概率为β2(0≤β2≤1).同时，系统是允许人员自由进出的，本文假设进入该系统的人员只能是知识接收者，退出系统的人员可以是知识接收者、知识传播者和知识遗忘者.令进入系统和退出系统的概率都为μ(0≤μ≤1).

图1 知识传播示意图Fig.1 Diagram of knowledge transmission

假设知识传播系统在不相关的异构网络中，其中p(k)表示度分布表示平均网络度，Sk(t)、Ik(t)、Hk(t)分别表示在时间t时度为k的知识接收者、知识传播者和知识遗忘者节点的密度.并且Sk+Ik+Hk=1.若I节点的度为k′，则I有k′条自由连接的边，故所选边指向度为k′的I节点的概率为：

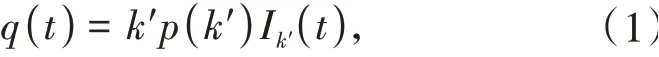
因此任意给定边在时间t指向I节点的概率为：应用平均场理论［14］，SIH模型可以表示如下：

其中0≤Sk(t)，Ik(t)，Hk(t)≤1，Sk(t)+Ik(t)+Hk(t)=1，t≥0.

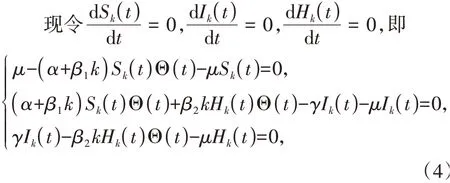
解得

将Ik代入（2）得到一个自洽方程

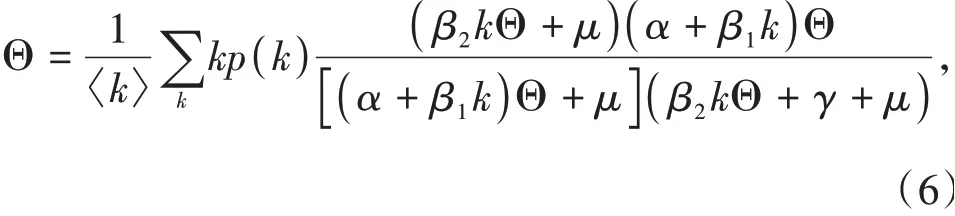
令

显然f(0)=0，0＜f(1)≤1.下面讨论（7）非零点的存在性.

当α+β1k＞β2k时，由 于0≤γ≤1，则α+要使f(Θ)=0的非零解存在，则须满足：

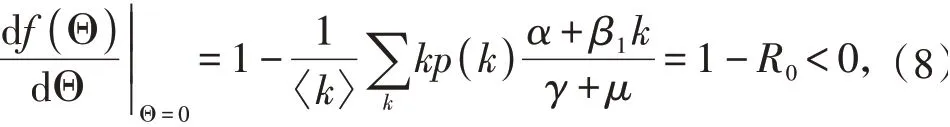
图2 函数f示意图Fig.2 Schematic diagram of function f

2 稳定性分析

本节将分析模型（3）的两个平衡Θ0和Θ*的全局渐近稳定性.

定理2.1若R0＜1，则无知识均衡Θ0(1，0，0)全局渐近稳定.

证明由于Sk+Ik+Hk=1，则Sk=1-Ik-Hk，将其代入（3）的第二个方程中有：

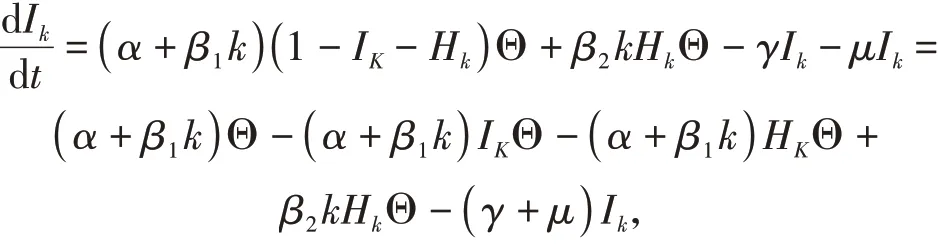
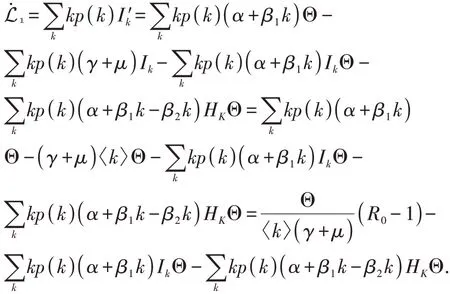
定理2.2当R0＞1时，知识地方均衡Θ*(S*，I*，R*)全局渐近稳定.

证 明在V：(Sk(t)，Ik(t)，Hk(t))∈Ψ：Sk（t），Ik（t），H（kt）＞0}→R上定义李雅普诺夫函数

显然对于所有Sk≠S*，Ik≠I*和Hk≠H*有L＞0.则对L2求导，有：

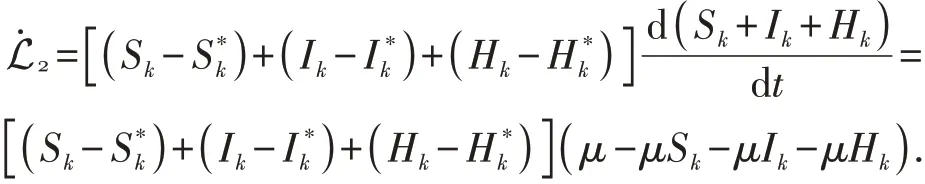
又由（4）有

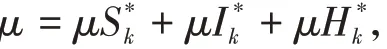
则有：

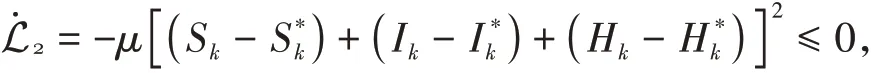
当且仅当Sk=S*，Ik=I*和Hk=H*等号成立.注意到只有当R0＞1时，S*、I*和H*才存在.由拉塞尔不变集原理（Lasalle invariance principle），当R0＞1时，知识地方均衡Θ*(S*，I*，R*)全局渐近稳定.

证毕.

3 仿真

为了证实第二节中的理论分析结果，本节将进行数值仿真，并且将进一步研究模型参数即自学水平α，熟人影响β1以及遗忘水平γ对于知识传播的影响.与随机增长网络、小世界网络和规则网络相比，知识在无标度网络更容易传播［8］.因此，本文在无标度网络中模拟知识传播.假设网络的初始节点为5个，这5个节点随机连边，随后依次加入5个新节点连接5条边直至达到1000个节点为止.知识传播由初始传播者发起，本文将初始传播者视为传播种子，并假设在传播初始阶段只有10个传播种子，其余全为知识接收者.令α=0.2，β1=0.01，γ=0.3，μ=0.2，β2=0.01，则有R0=0.8100＜1.如图3所示，知识接收者先减少再增加到1；知识传播者减少到0；而知识遗忘者先增加到一个最大值后再减少到0.当R0＜1时，系统最后只有知识接收者，知识不能传播，这证实了定理2.1.令α=0.3，β1=0.05，γ=0.3，μ=0.2，则有R0=2.7014＞1.如图4所示，知识接收者先快速下降再缓慢下降，最终达到稳定；知识传播者和知识遗忘者都先快速增加再缓慢增加，最终达到稳定状态.当R0＞1时，知识能够传播，并且三个群体都趋于一个正值，这证实了定理2.2.

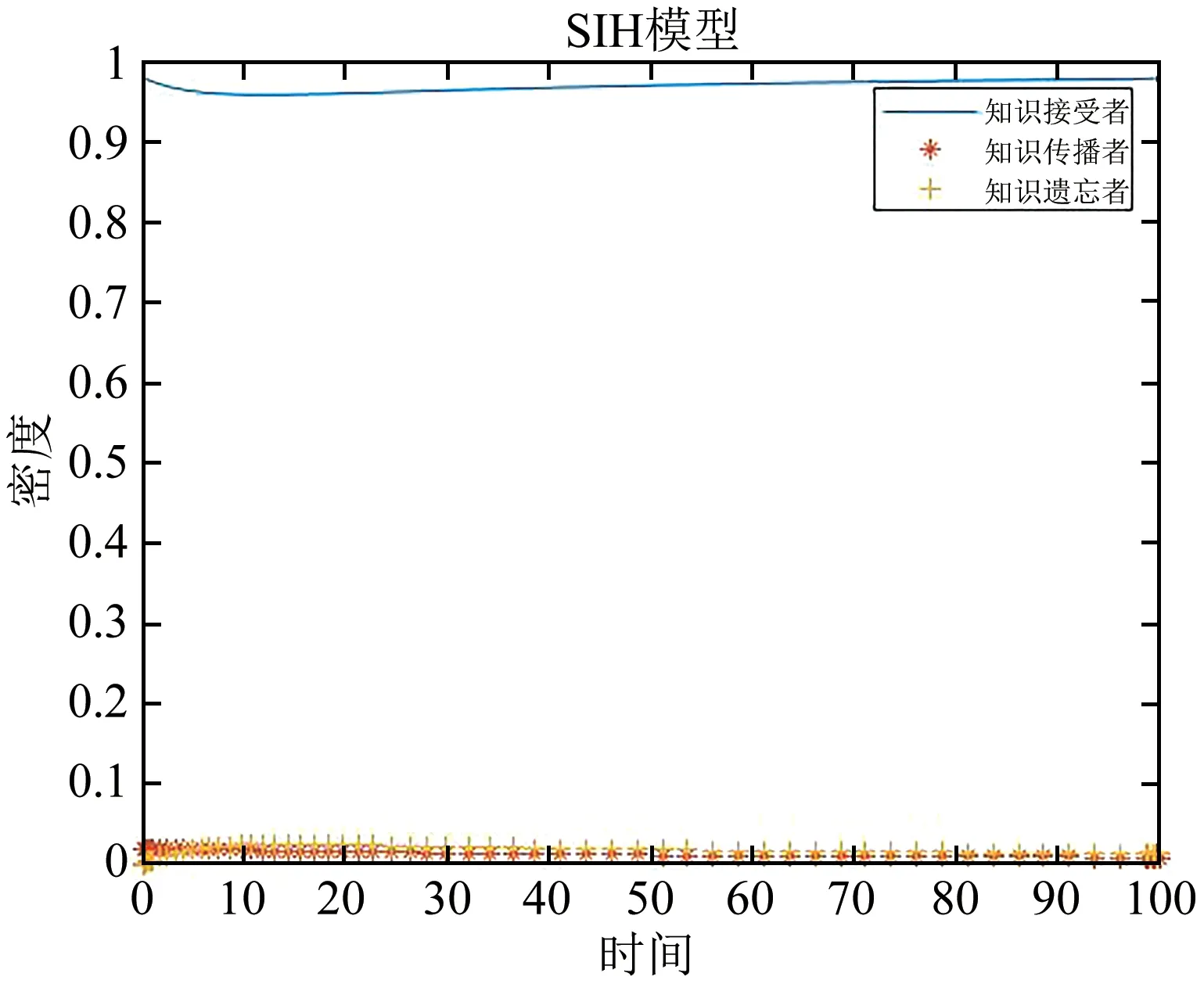
图3 R0＜1时人群密度变化图Fig.3 Graph of the density of population changing when R0＜1

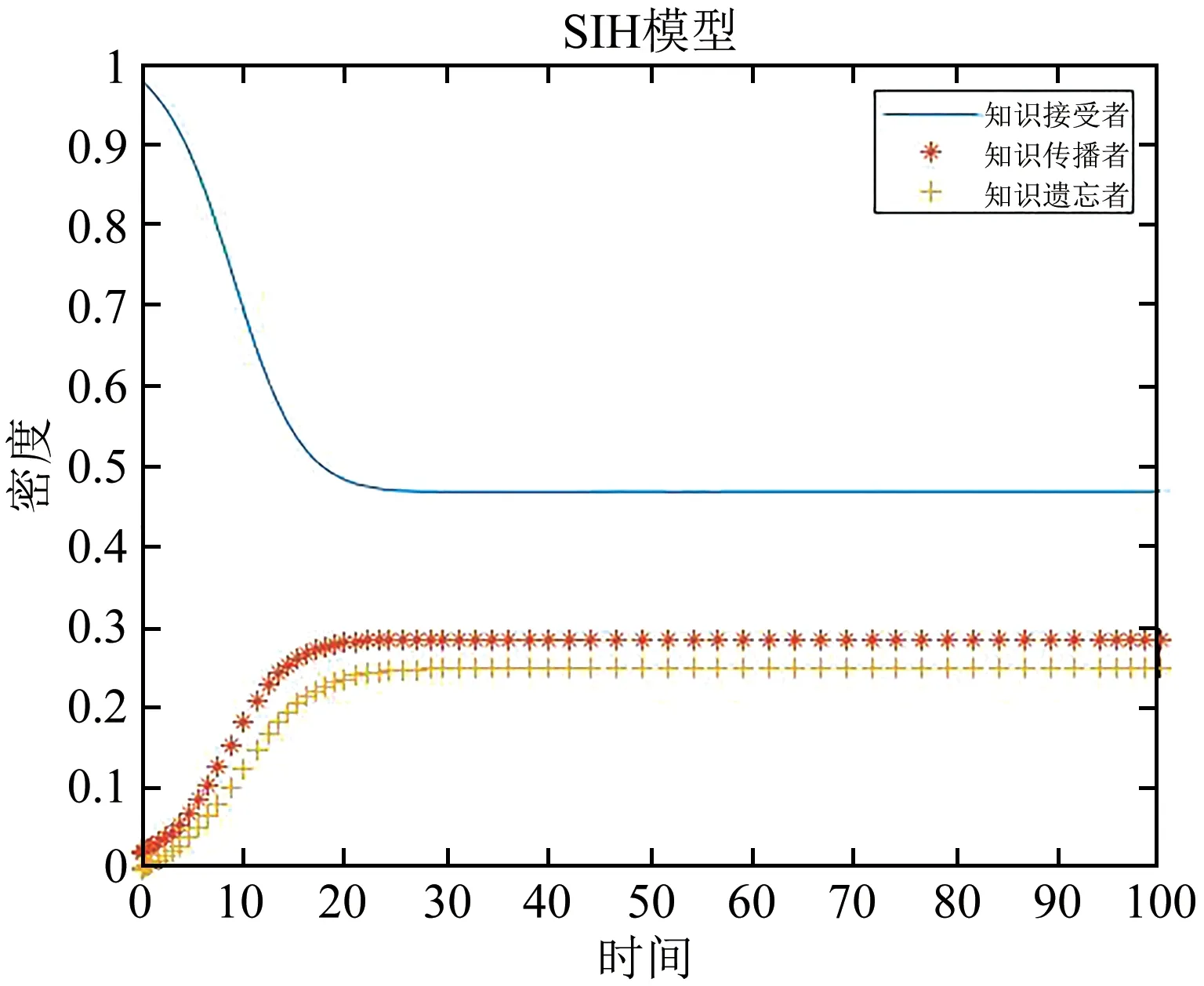
图4 R0＞1时人群密度变化图Fig.4 Graph of the density of population changing when R0＞1

令β1=0.05，γ=0.3，μ=0.2，β2=0.01，如图5所示，Ik随着α增加的而增加.知识接收者自学水平越高，知识传播者的密度就越大，并且知识传播者达到稳定状态所需要的时间越少，即知识传播越快.

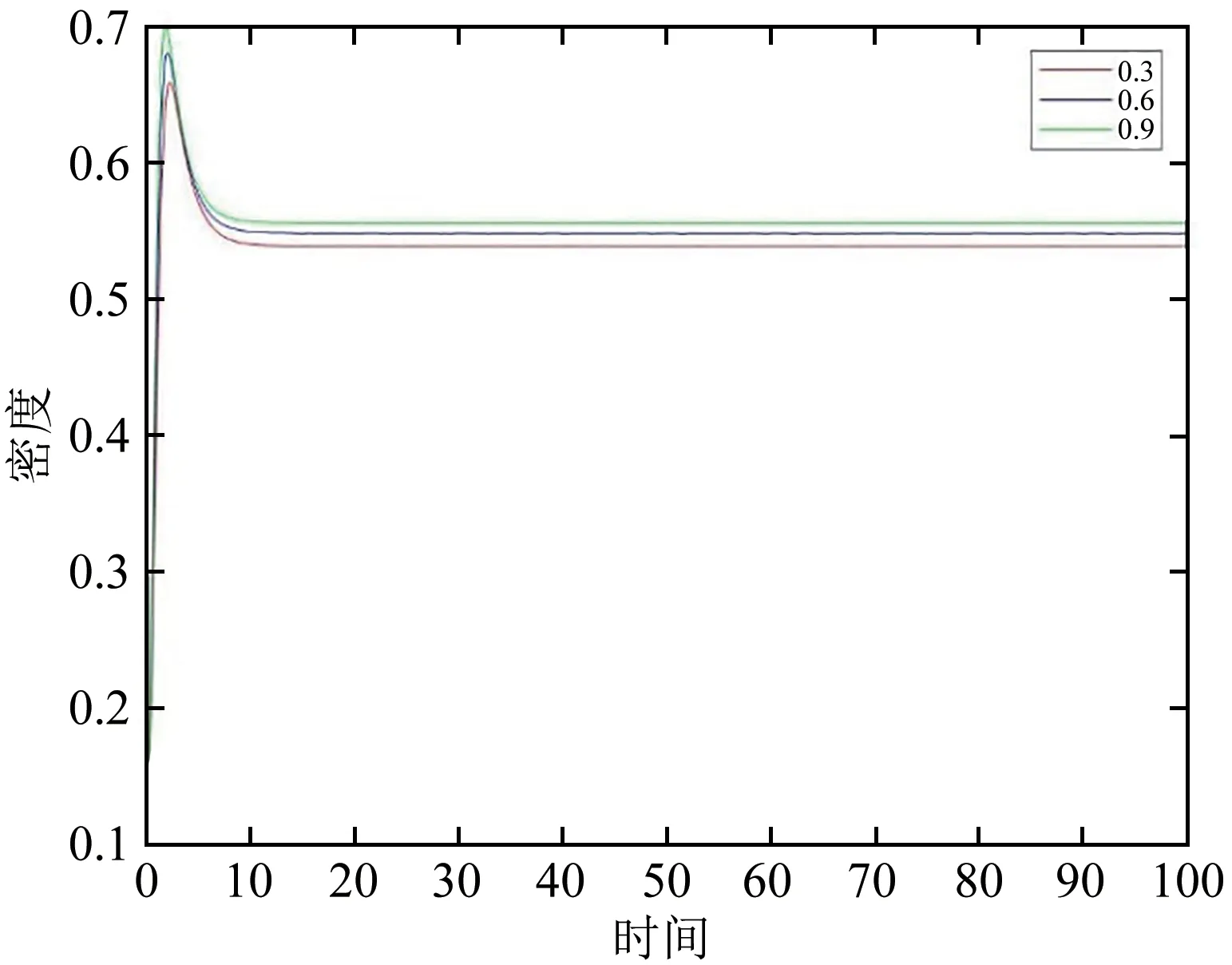
图5 α=0.3，0.6，0.9知识传播者密度变化图Fig.5 Diagram of the density of knowledge disseminators changing when α=0.3，0.6，0.9

令α=0.2，γ=0.3，μ=0.2，如图6和图7所示，Ik随着β1和β2的增加而增加.知识接收者和知识遗忘者周围熟人越多，熟人影响越大，知识传播 者 的 密 度 也 就 越 大.令α=0.2，μ=0.2，β1=0.05，β2=0.01，如图8所示，Ik随着γ的增加而减少.知识传播者的遗忘水平越大，知识传播者就越少.

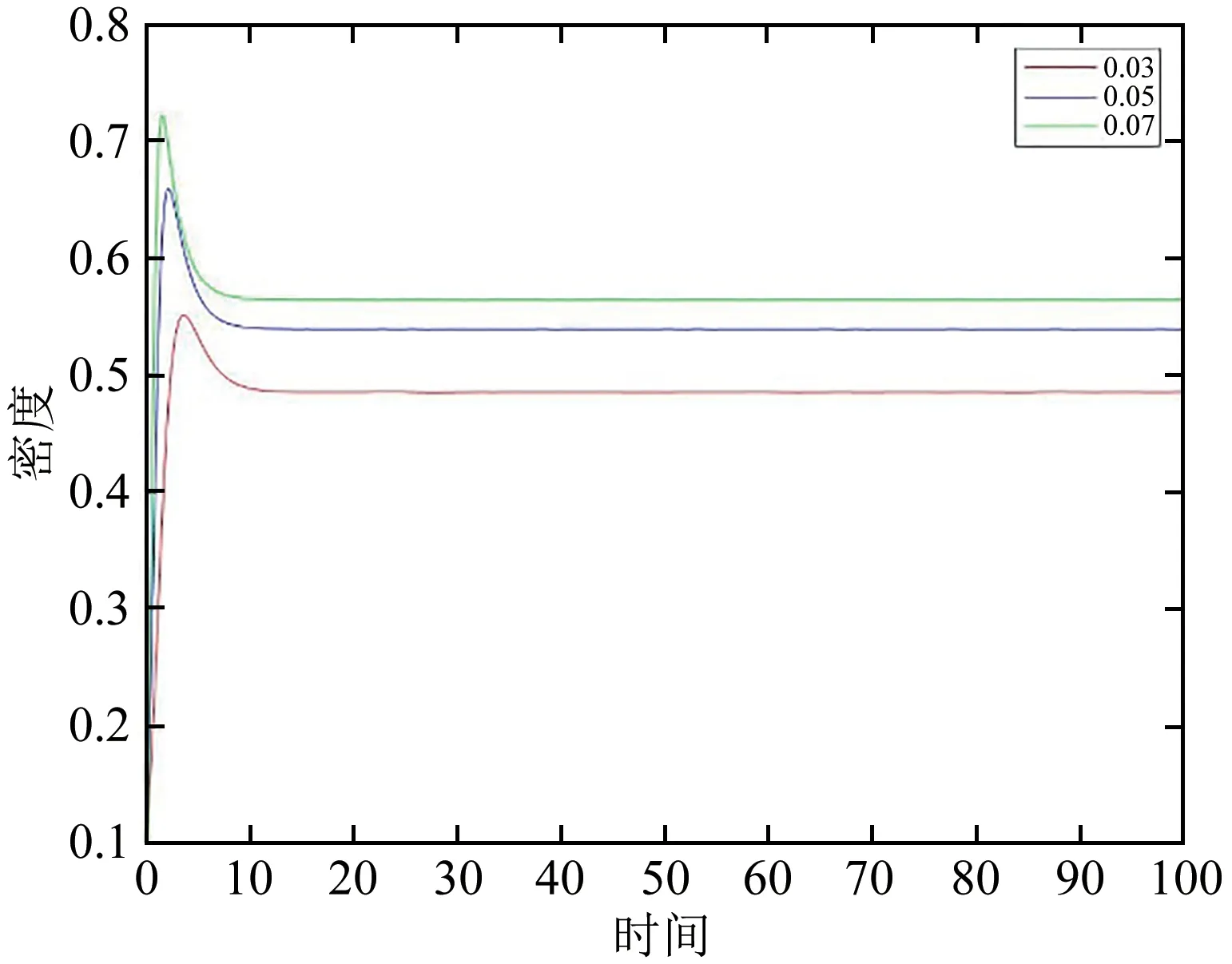
图6 β1=0.03，0.05，0.07知识传播者密度变化图Fig.6 Diagram of the density of knowledge disseminators changing when β1=0.03，0.05，0.07

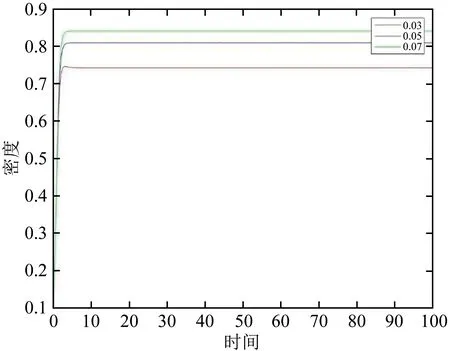
图7 β2=0.03，0.05，0.07知识传播者密度变化图Fig.7 Diagram of the density of knowledge disseminators changing when β2=0.03，0.05，0.07

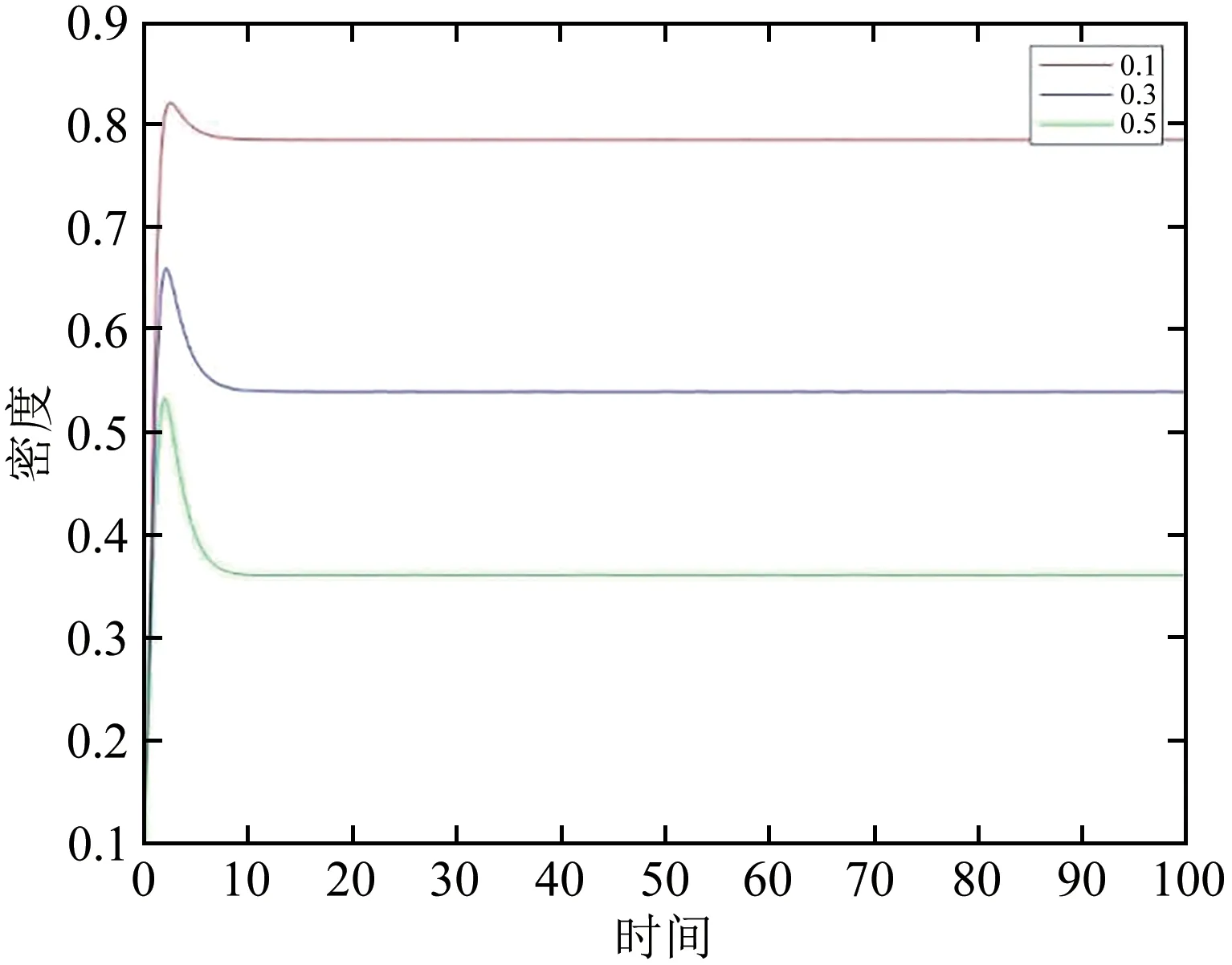
图8 γ=0.1，0.3，0.5知识传播者密度变化图Fig.8 Diagram of the density of knowledge disseminators changing when γ=0.1，0.3，0.5

4 结论

本文首次通过考虑熟人作用，在复杂网络中建立了SIH模型.熟人在知识传播中起着分享知识、反馈知识以及提醒知识的作用.知识接收者有两个方式获取知识，一个是通过熟人分享获取，另一个则是通过自学获取.另外，每个人的记忆力有限，保存知识的时间也有限，知识遗忘者可通过熟人的提醒而重新获取知识.本文还对知识传播的动态性能进行理论分析，发现当R0＜1时，系统最终只有知识接收者人群，知识无法传播；当R0＞1时，系统最终有知识接收者、知识传播者和知识遗忘者三种人群，知识可以传播.通过在无标度网络中的数值仿真，我们证实了理论分析的正确性，并且发现知识传播者的密度与自学水平和熟人作用呈正相关，与遗忘水平呈负相关.在现实生活中，为了提高知识传播水平，可以采取以下措施：

1）提高知识接收者的自学水平；

2）增加知识接收者和知识遗忘者周围熟人的人数，提高熟人的作用力；

3）知识传播者及时回顾或者将知识多应用于实践以减少遗忘水平.

知识在人群中的传播机制是复杂多样的.本文只考虑了自学水平、熟人作用以及遗忘水平，另外本文只采用平均场方程在无标度网络中进行数值仿真，具有单一性.接下来我们将在这些方面进行改进.