一类电压采样电阻异常的电能表计量失准研究

朱铮，陈海宾，蒋超，甄昊涵，许堉坤，童涛

（国网上海市电力公司电力科学研究院，上海 200437）

随着专变用户量增加，电能表抄表运维管理工作量增大，抄表工作已从人工抄表升级为自动化抄表［1-2］.目前，智能电能表能够实现每15 min记录一次数据，成为智能电网的核心设备.虽然记录效率提高了，但计量装置故障率高却成为当前面临的一个挑战，尤其是电能表计量失准问题.异常计量设备难以准确记录和反映用户的真实用电情况，给电网公司或者用户造成了一定的经济损失［3-4］.

电能表计量失准通常分为自然失准和人为失准［5］.自然失准表现在设备内部元件质量不合格或在恶劣环境使用时间过长而导致电能表计量异常；而人为失准即以人的主观意愿更改电能表内部元件使得设备计量误差增大，给用户的用电安全带来隐患.

近年来，有许多关于电能表计量异常的研究成果［6-9］，其基本思想是根据数据建立模型，分析并确定计量异常的阈值，进而得到判定模型.文献［10］从用户用电负荷角度出发，利用组合优化后的灰色模型，构建了带有阈值的预测模型，当用户负荷数据在负荷阈值的范围之内，说明电能表计量正常，否则判定电能表计量异常.文献［11］通过电能表数据分析出用户用电的峰值需求，从四个时间段对数据进行聚类分析，再分组得出异常用户.文献［12］对时间序列进行分析，构建数据点距离模型来检测离群点的范围，从而对电能表的计量异常进行判定.然而这些方法只是从数据本身出发建立相应的预测模型，未从硬件方面深入剖析，导致在实际应用中数据异常报警重复或者报警数据量大而难以找到异常关键点.

针对上述问题，本文提出了基于神经网络的电能表计量失准判定方法.首先，归纳计量失准原因，建立硬件中电压采样电阻与电压采样值之间的关系.然后构建神经网络模型训练电压数据获得电压采样值的残差.同时给出残差的马氏距离控制限的确定方法，从而设计计量失准判定规则.最后，通过仿真验证了本文所提出方法的正确性和有效性.

1 电能表计量失准原因分析

电能表计量主要受硬件、软件、生产工艺以及环境因素影响［13-15］.硬件方面表现在电路设计和通讯线路不可靠，当电压采样电阻异常或线路受到干扰时就会导致数据读写出现偏差；在软件方面，电能表在快速停复电时，主处理器未能成功将配置参数写入计量芯片，后续程序也未能及时对计量芯片的配置参数进行校验而导致计量失准；工艺原因有元件受力不均、电路板部分元件受到灰尘污染、无涂抹三防漆或者涂抹不到位等；同时电能表所处的环境的温度、空气湿度和网络稳定性都会影响其正常运行，长期处于恶劣环境的电能表会大幅度减少其使用寿命，影响计量精度.

典型电能表计量设计示意图如图1所示，以单相智能费控电能表（DDSK）为例，计量芯片设计时会涉及校表参数和计量参数两部分［16］.通常，校表参数影响计量误差的准确度，计量参数影响芯片计算的准确度.当计量芯片硬件电路某部分发生更改或者计量芯片校表参数出现偏差时，就会造成软件流程误判，使计量数据发生偏离.

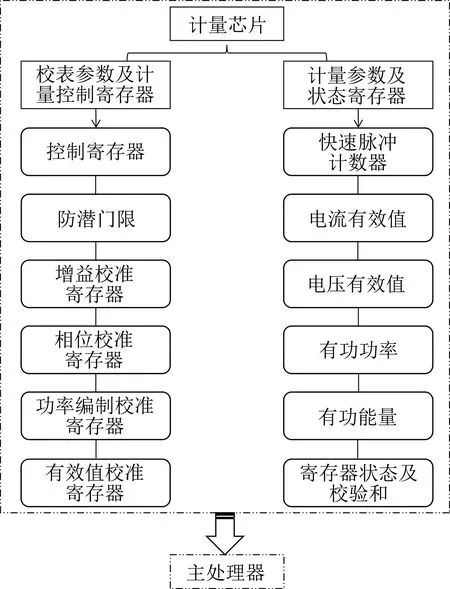
图1 典型电能表计量设计示意图Fig.1 Schematic diagram of typical watt hour meter metering design

在实际应用中，如果出现人为更改器件导致电阻损坏、虚焊以及阻值发生变化这一类窃电行为或者元件自然故障，均优先考虑电压采样电阻阻值发生变化.图2为型号ATT7053BU的计量芯片部分电路示意图，芯片中的24个引脚连接相应的电路，电路中的电阻、电容均为精密元件，当出现异常时会影响芯片的校表参数和计量参数.

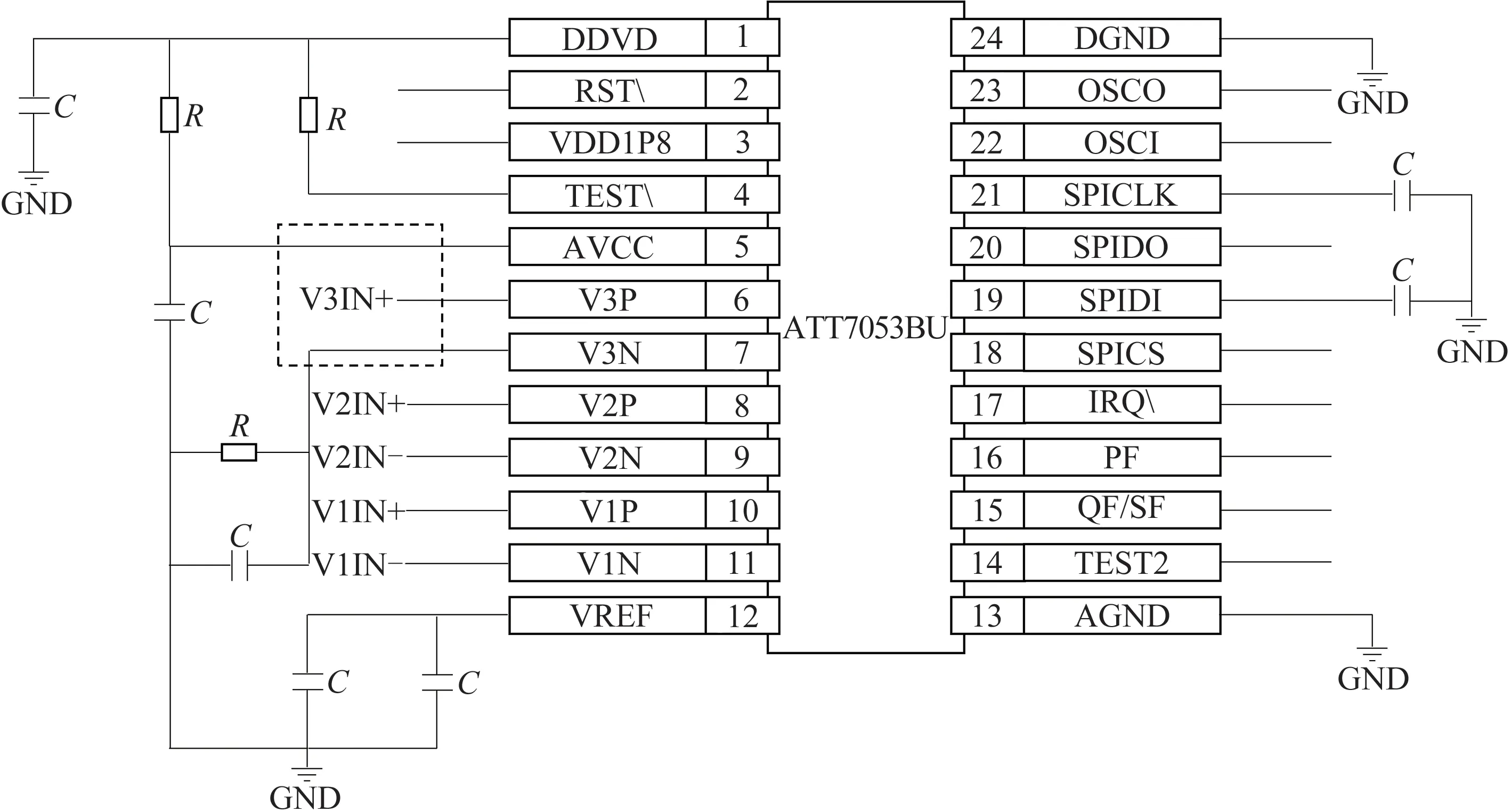
图2 计量芯片部分电路示意图Fig.2 Schematic diagram of metering chip circuit

在计量芯片电路中，第6引脚为V3IN+电压采样电路，如图3所示，R1～R6为电压采样电阻.通常，定义电阻R6两端的电压为电压采样值，R1～R5在电路中起到分压作用；C代表电容.正常情况下，R1～R5阻值为200 kΩ，R6阻值为1 kΩ；N和L分别表示零线和火线，GND表示接地.

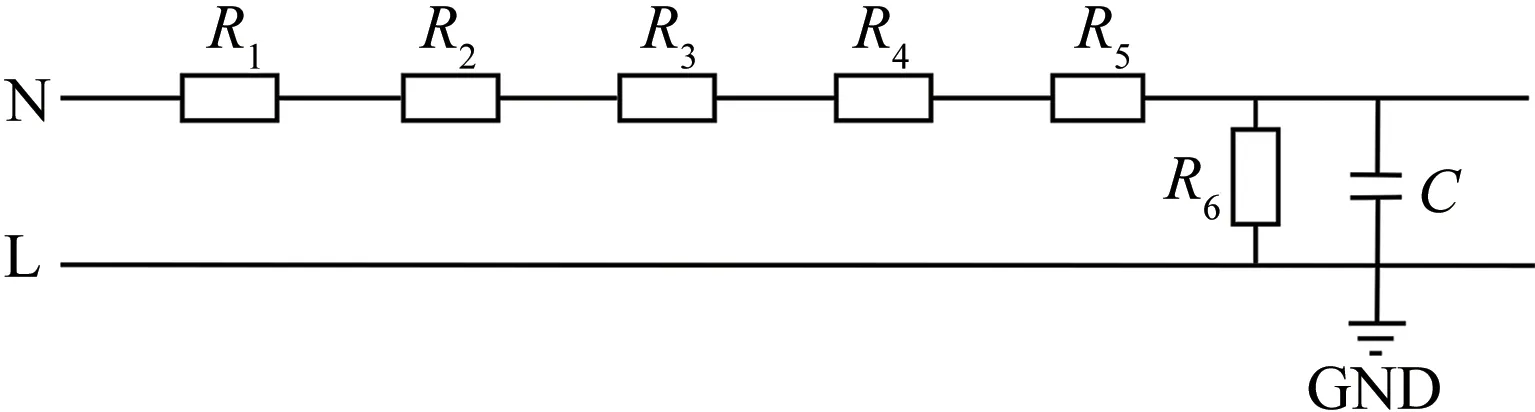
图3 V3IN+电压采样电路示意图Fig.3 Schematic diagram of V3IN+voltage sampling circuit

设Vs为电压采样值，在电能表运行正常情况下，通过电阻分压可以得到：

其中，U源为源电压值.将串联部分电阻记为Ra，并联部分电阻记为Rb，如图4所示，源电压在串联、并联电阻的分压下得到电压采样值.设电能表反馈的电压有效值为Vf，则Vf可经Vs换算得出.

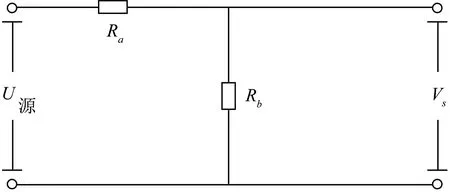
图4 电阻分压示意图Fig.4 Schematic diagram of resistance partial voltage

结合现场运行反馈的故障现象，将电阻异常导致的计量失准原因分析如下：

（1）串联部分电阻Ra增加.此时可将式（1）写为：

其中ΔRa为串联部分电阻的增加量.当ΔRa增大时，Vs减小，从而影响Vf.

（2）并联部分电阻Rb增加.此时式（1）可以

写为：

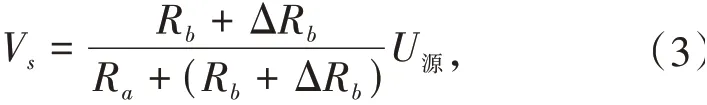
其中ΔRb为并联部分电阻的增加量.为保护计量芯片稳定，并联部分电阻要远小于串联部分电阻，这使得电压采样值对ΔRb的变化极其敏感，当ΔRb逐渐变大时，Vf会显著变大，出现表记飞走现象.

（3）电容C失效.当电容C受到分板应力影响或本身器件问题而处于似断非断状态时，极易导致失效现象.

当发生电容失效现象时，电容C变为电阻R7，此时得到：

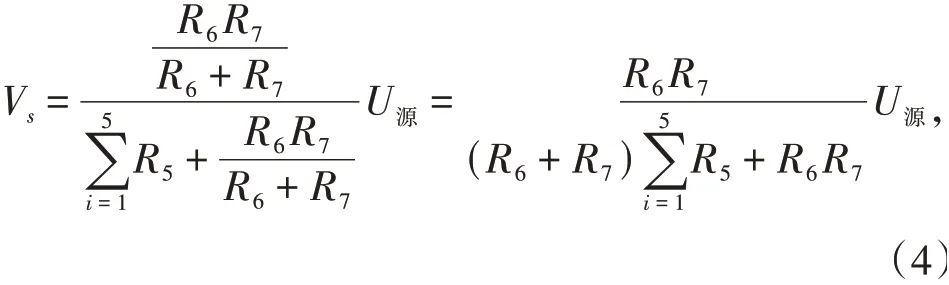
记电阻R6和电阻R7并联后的电阻为R~6，则R~6＜R6且即并联部分电阻Rb减小.

通过式（2）、式（3）和式（4）发现，电阻阻值和电容状态可以影响电压采样值，电容失效现象可视作电路中电阻发生变化.

表1给出了电压采样电阻的阻值变化对电压采样值的影响状况，第一行数据为正常运行数据，当串联部分电阻增加，并联部分电阻不变时，电压采样值显著减小；当串联部分电阻不变，并联部分电阻增加时，电压采样值显著增大；通常，并联部分电阻R6较小，与R7并联之后对电压采样值的影响不显著.另外，未及时滤除杂波干扰的异常电容会影响计量精度，因此排查并联部分电阻异常时，仍然需要对电容进行检测和分析.

表1 电压采样值在电阻阻值异常的变化状况Tab.1 Variation of voltage sampling value in abnormal resistance value

2 构建神经网络模型

本文从硬件中电压采样电阻阻值的变化状况出发，将电能表监测数据分为离线和在线数据两部分.如图5所示，对于离线数据，首先，对电能表的历史数据进行预处理，将电能表运行相关变量作为神经网络模型的输入，并进行训练，再将电能表的正常运行数据输入神经网络模型中，计算出输出数据与实际数据之间的残差以计算马氏距离，最终得到电能表失准阈值.针对在线部分数据，将电能表实时数据进行预处理，再输入训练好的神经网络模型中，同离线部分相仿，计算残差和马氏距离并与失准阈值比较，进而判断电能表计量是否异常.

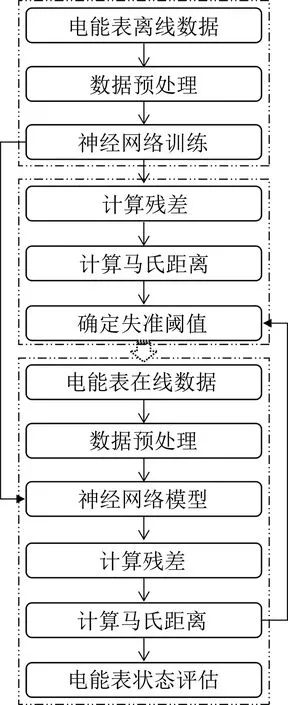
图5 电能表状态评估流程Fig.5 State evaluation process of electric energy meter

为得到神经网络模型，将利用神经网络对电能表离线数据进行训练.如表2所示，设定神经网络的模型参数.

表2 神经网络模型参数设定Tab.2 Parameter setting of neural network model

本文考虑单输入单输出的神经网络模型，选取Vf作为模型输入，Vs作为模型输出；隐含层神经元个数根据公式给出，其中m为隐含层神经元个数，n为输入个数，l为输出个数，α为1～10之间的常数；通过仿真反复测试，1层隐含层以及3个隐含层神经元可以获得较好的拟合效果.根据表2构建神经网络的模型结构：

图6中输入值x为电能表所测的电压数据Vf，输出值y为电压采样数据Vs.在神经网络训练前，对输入的电压数据进行归一化处理：

图6 神经网络结构图Fig.6 Structure diagram of neural network

其中，xi表示向量x中对应的第i个值；xmax和xmin分别表示向量x中的最大和最小值；x′i表示数据归一化后的值.

计算模型输出值和实际值的残差：

引入拟合度指标：

根据r直观模型预测值和实际值之间的差异以及非线性函数的拟合程度，其中m表示样本的总个数；yi表示模型参数的实际值表示模型参数的预测值.r的值越接近1，说明模型的拟合性能越好.

本文引入马氏距离判别样本参数残差的差异，马氏距离可以避免受到量纲的影响，排除样本点之间相关性的干扰.将样本参数的残差作为输入得到：

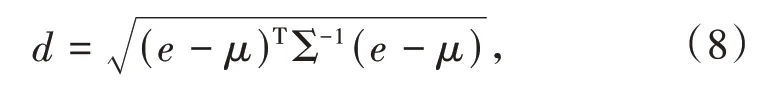
其中，d为样本参数的残差的马氏距离；e为残差组成的列向量；μ和Σ分别表示残差数据的均值向量和协方差矩阵.

采用核密度估计法确定马氏距离的阈值，构建样本点e^的概率密度函数f(e^)：

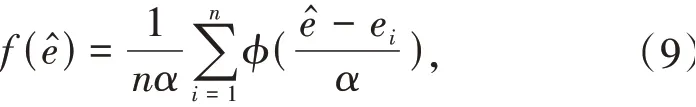
其中，α为窗宽；φ(·)表示核密度估计采用的核函数

满足φ(·)≥0且本文采用高斯核函数，在给定置信度β后，可通过概率密度函数的积分公式得到相应的控制限λ，即：

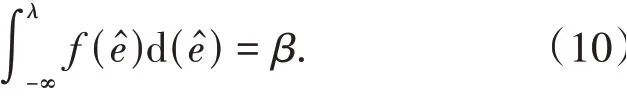
本文选定置信度为99.9%，根据式（10）确定失准阈值，若电能表实时运行数据的马氏距离超出阈值，则说明电能表可能计量异常.

3 仿真分析

基于上述理论分析，本节针对所提出的方法进行仿真验证.电能表每天从00∶00至24∶00隔15 min采样一次数据.对同一型号的3个运行正常的电能表，选取2022年1月1日至1月15日的离线电压数据共4320组，其中2880组作为训练数据，1440组作为测试数据.根据式（1）获得离线数据的电压采样值，将数据进行预处理后进行训练.训练中得到r=0.9983，从图7（a）可以看出，模型的预测值较好地拟合实际值，图7（b）中模型预测的误差变化基本稳定在0附近，说明此模型拟合性能优异.

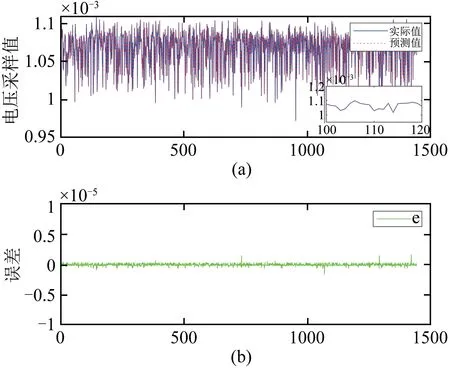
图7 神经网络训练性能Fig.7 Training performance of neural network

图8（a）为运行正常电能表某天的电压数据情况，将此数据输入到训练好的神经网络模型中，得到图8（b）中电压采样值以及图8（c）中电压采样预测值与实际值之间残差的变化情况.

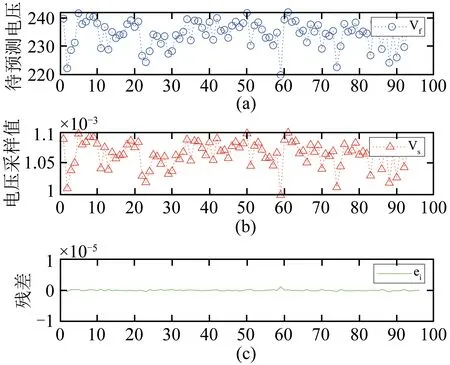
图8 神经网络训练的数据变化Fig.8 Data change of neural network training

针对训练的3个运行正常的电压表，选取2022年1月16日至1月30日的4320组电压数据，经过归一化处理之后，按照上述方式进行训练，将得到残差数据按照式（8）计算每个数据到总体数据的马氏距离.

为了评估电能表的运行状态，本文根据残差的马氏距离的控制限确定电能表的失准阈值.图9中给出了概率密度函数的频率直方图、核密度估计图和正态分布密度图.频率直方图与核密度估计图相比缺少了连续光滑的性质，不便于求解控制限；正态分布密度图则掩盖了大部分的数据分布结构，使得求解的控制限不准确.

图9 不同估计方法的概率密度函数Fig.9 Probability density functions of different estimation methods

本文选取高斯核密度估计法求解控制限，图10中窗宽为0.5概率密度函数图像较好的展示了数据分布结构，相较于MATLAB工具箱中的默认窗宽更加平滑；随着窗宽变大，概率密度函数图像趋于平滑，却掩盖了数据分布结构.因此，对正常的电压数据所训练得到的残差数据，选取窗宽为0.5的概率密度函数，根据式（9）、式（10）得到控制限λ=9.35，若此时残差的马氏距离大于λ，则说明该电能表计量异常.

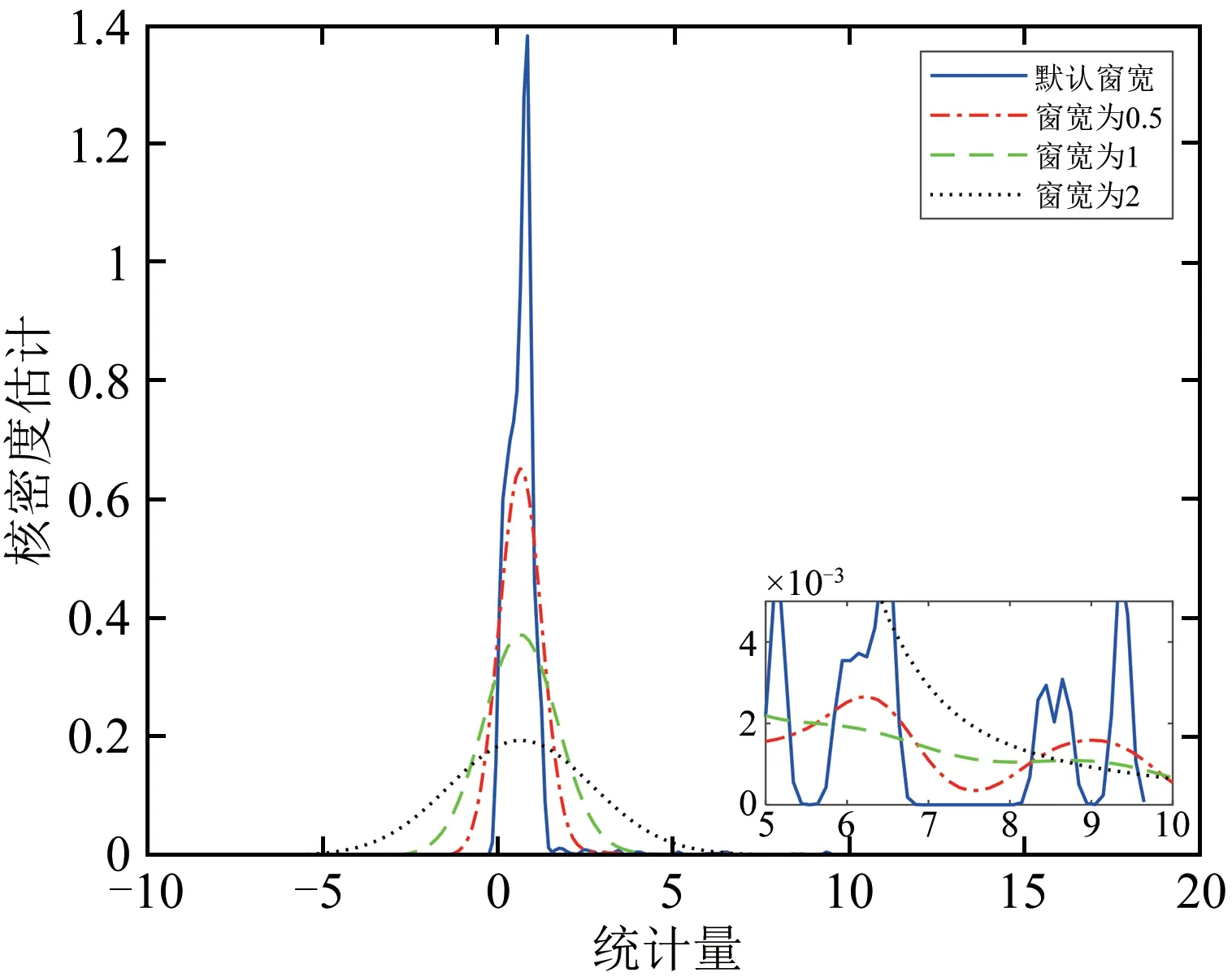
图10 不同窗宽的核密度估计法Fig.10 Kernel density estimation method with different window widths

将2022年2月1日至2月5日的异常电能表Ⅰ、电能表Ⅱ运行数据经过预处理之后，由神经网络模型输出，得到电压采样值的残差的马氏距离的变化状况.如图11所示，电能表Ⅰ在2月2日开始出现异常，随着时间推移，异常点增多，在2月6日左右超出控制限.图12中的电能表Ⅱ的异常状态持续时间短，波动幅度大且迅速超出控制限.将电能表拆回后分析发现，电能表Ⅰ的计量芯片的串联部分电阻中R2阻值异常，从200 kΩ变变到7.4 MΩ，导致表记频繁掉电；电能表Ⅱ则是计量芯片的并联部分电阻中R6阻值异常，从1 kΩ变到2.2 kΩ，此时电压有效值Vf显著变大，出现计量飞走现象.通过观察和分析数据可以发现，异常数据在超出控制限之前会提前发生波动，使得其他数据处于平稳状态.

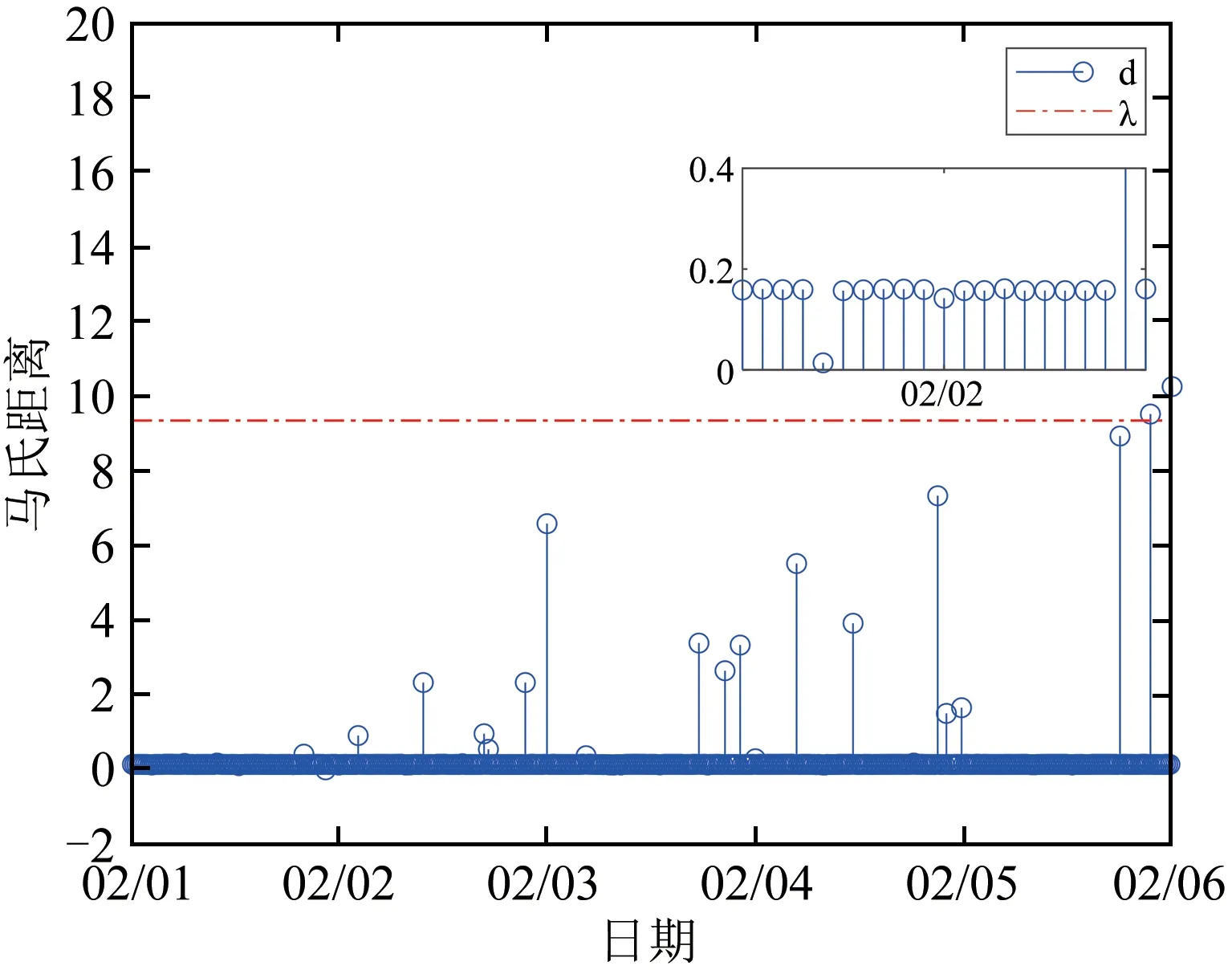
图11 异常电压表Ⅰ的马氏距离Fig.11 Mahalanobis distance of abnormal voltmeterⅠ

图12 异常电压表Ⅱ的马氏距离Fig.12 Mahalanobis distance of abnormal voltmeterⅡ

图13和图14分别选取相同时间段运行正常的电能表Ⅲ、电能表Ⅳ的数据，和异常电能表的数据处理相似，得到了电压采样值的残差的马氏距离与控制限之间的变化状况，且马氏距离均处于控制限之下.

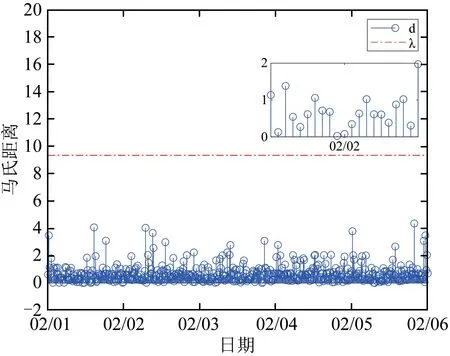
图13 正常电压表Ⅲ的马氏距离Fig.13 Mahalanobis distance of normal voltmeterⅢ

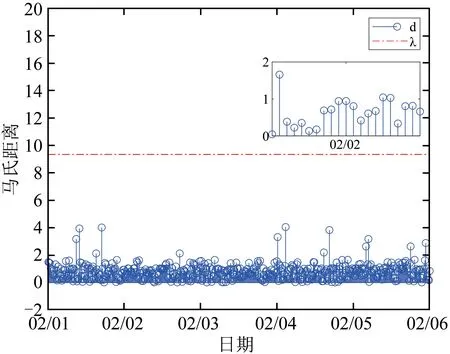
图14 正常电压表Ⅳ的马氏距离Fig.14 Mahalanobis distance of normal voltmeterⅣ

本文设计控制限λ作为电能表计量失准的阈值，当统计量d大于此阈值时，判定计量异常.运用此阈值可以在计量失准前及时安排检修或更换，避免严重的计量失准事故发生.

4 结语

本文分析了电能表计量失准原因，从硬件方面分析电压采样电阻的有效值对计量精度的影响.通过构建神经网络模型，对电压采样值的实际值与预测值之间的残差进行训练，借助核密度估计法得到了残差的马氏距离的控制限.通过仿真分析发现，控制限可以很好地判别电能表的计量状态.此外，通过训练得到的马氏距离也可以提前预判电能表的计量异常状态.