基于Transformer模型与毫米波雷达的手势识别
2022-11-02余玟铮殳国华匡政睿
余玟铮, 殳国华, 匡政睿
(上海交通大学 电子信息与电气工程学院,上海 200240)
0 引 言
手势识别作为人机交互的重要环节,一直是国内外研究学者的重点研究领域。目前常见的手势识别技术可分为三类,基于图像的手势识别对环境要求较高,且涉及到用户隐私;基于传感器信号的手势识别操作繁琐;基于无线电信号的手势识别受限于无线信号的带宽和频点,容易受干扰,无法大量使用。毫米波雷达具有空间分辨率高,穿透能力强,受环境影响小的特点,在手势识别应用中具有独特的优势。
基于毫米波雷达的手势识别采用调频连续波(frequency modulated continuous wave, FMCW)雷达。通过对雷达信号的混频与调制处理,可以对目标的距离、速度和角度进行估计,得到相应的特征谱;再利用深度神经网络实现手势动作的分类识别。2016年谷歌公司的Soli芯片[1],大幅缩减雷达的体积与功率,提升了算法效率。2017年德州仪器公司利用雷达提取手势的距离和多普勒谱图[2],并采用隐含马尔柯夫模型进行检测和识别。重庆邮电大学的王勇教授[3]利用77 GHz FMCW雷达,将卷积神经网络(convolutional neural networks,CNN)与高维特征相融合,实现了较高的手势识别率。电子科技大学的王亚龙[4]重点研究了串联式架构网络算法、基于多维度输入的长短期记忆(long short-term memory, LSTM)网络,提高了手势识别率。
本文提出了一种基于77 GHz毫米波雷达的手势识别算法,通过参数设计选择了合适的分辨率,在对雷达信号进行预处理后,利用多维快速傅里叶变换(fast fourier transformer, FFT)得到目标手势的距离、速度参数信息,并借助Transformer网络完成手势的分类与识别。
1 FMCW毫米波雷达基本原理
1.1 毫米波雷达的工作原理
本文采用的毫米波雷达设备为德州仪器公司发布的AWR1443BOOST型号开发板,该FMCW设备覆盖76~81 GHz频带,可用带宽为4 GHz,具有4个接收天线和2个发射天线,6个通用ADC(analog-to-digital converter)端口。本文使用4个接收天线与1个发射天线。
图1给出了AWR1443雷达信号的调频方式,通过对雷达参数的配置可以实现不同的雷达监测效果。本文选用的FMCW雷达调制方式为锯齿波调制[5],雷达的发射信号如式(1)所示。
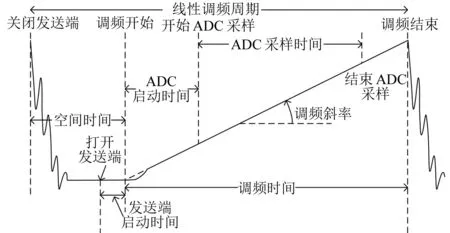
图1 毫米波雷达线性调频脉冲信号

(1)
式中:AT为发射信号的幅值;fT(τ)为频率;fc为载波的中心频率。fT(τ)随着时间τ的增大而线性增加,可表示为fT(τ)=S·τ。其中:S为信号斜率,S=B/Tc;Tc为线性调频波的脉宽;B为线性最大带宽。
根据接收到回波脉冲的时延和物体移动引起的多普勒频移,可以得到雷达的接收信号如式(2)所示。

(2)
式中:AR为接收信号的幅值;fR(τ)为频率;Δtd为从发射到接收到回波信号的时延,Δtd=2(R+vt)/c;R为目标距离;v为目标速度;c为光速。考虑到物体移动的多普勒频移Δfd=-2fcv/c,可将雷达的接收信号的频率fR(τ)表示为式(3)。
fR(τ)=S·(t-Δtd)+Δfd
(3)
将发射信号与接收信号进行混频后,再通过低通滤波器可以得到中频信号,表示为式(4)。
sIF(t)=fLPF{sT(t)·sR(t)}=

(4)
FMCW雷达信号的频率是随着脉冲时间的增加不断抬高的,因此可以根据回波信号的频率信息估计出目标的距离,具体计算公式见式(5)。通过对多个脉冲扫频的累计可以探测到相同距离处不同的相位,相位差可表示为式(6),速度与相位差之间的关系如式(7)所示。
(5)
Δω=2πΔfd(t1-t0)=2πΔfdTc
(6)
(7)
考虑到雷达信号采样率的限制,根据式(5)可得目标最大检测距离如式(8)所示。Tc周期内的采样点数Ns=Tc·Fs限制了雷达的距离分辨率,如式(9)所示。
(8)
(9)
在对目标信号进行速度估计时,需要对回波信号的相位差进行限制,即Δω<π,故目标最大检测速度如式(10)所示。在分析目标检测速度的分辨率时,需要考虑扫频个数Nc的限制,即当Δω>2π/Nc是可以分辨两个目标,由此可得速度分辨率如式(11)所示。
(10)
(11)
1.2 毫米波雷达参数设计
表1给出了本文所使用的雷达参数值。

表1 雷达参数设置
1.3 雷达数据处理
雷达前端的接收天线接收到回波信号,将其与发射信号进行混频,得到频率稳定的中频信号。对混频产生的中频信号进行ADC采样,得到雷达的时域信号,对该信号进行加窗操作之后要进行两次快速傅里叶变换(fast fourier transform, FFT)变换。对扫频采样得到的雷达数据进行第一次FFT变换可以得到频率信息,即距离信息。第二次FFT利用多个重复的扫频数据中同频信号的相位变化进行多普勒估计,可以得到距离多普勒谱,再在距离多普勒谱中进行峰值搜索可以得到手势的多普勒频偏值,即多普勒谱。在得到距离谱与多普勒谱之后进行恒虚警检测,过滤杂波干扰,提取出感兴趣的目标,并将距离谱与多普勒谱形成序列,方便后续模型的输入。
2 Transformer模型的构建
Transformer模型是一个自然语言处理模型,其网络架构模型如图2所示。传统的循环神经网络在处理长时间序列的问题时,会出现梯度消失与梯度爆炸等问题,LSTM网络对长序列的记忆能力有了较大改善,但对于超长序列仍存在问题。注意力机制的提出消除了输入输出之间距离的影响,根据长时间序列的依赖关系进行序列建模。Transformer模型利用全局自注意力机制,能够捕捉到输入序列和输出序列的依赖关系。
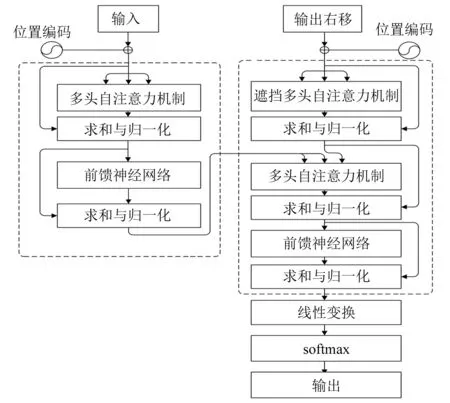
图2 Transformer网络模型
Transformer模型本质是N层编码器(encoder)与解码器(decoder)的结构,编码器包含多头注意力机制和前馈神经网络两个子层,解码器还额外包含遮掩多头注意力机制子层。
编码器负责将输入的手势特征序列进行编码,主要依靠多头自注意力机制,模型结构见图3。通过计算特征向量间的相似度来表征序列相关性,以解决长时间序列的依赖。自注意力机制通过缩放点积注意力来计算特征向量的注意力值,模型结构如图4所示。
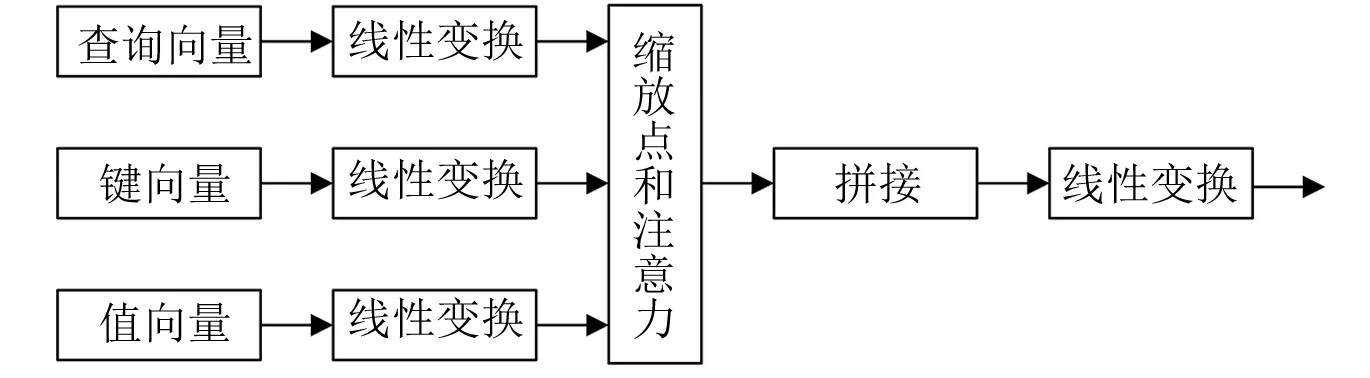
图3 多头自注意力模块结构
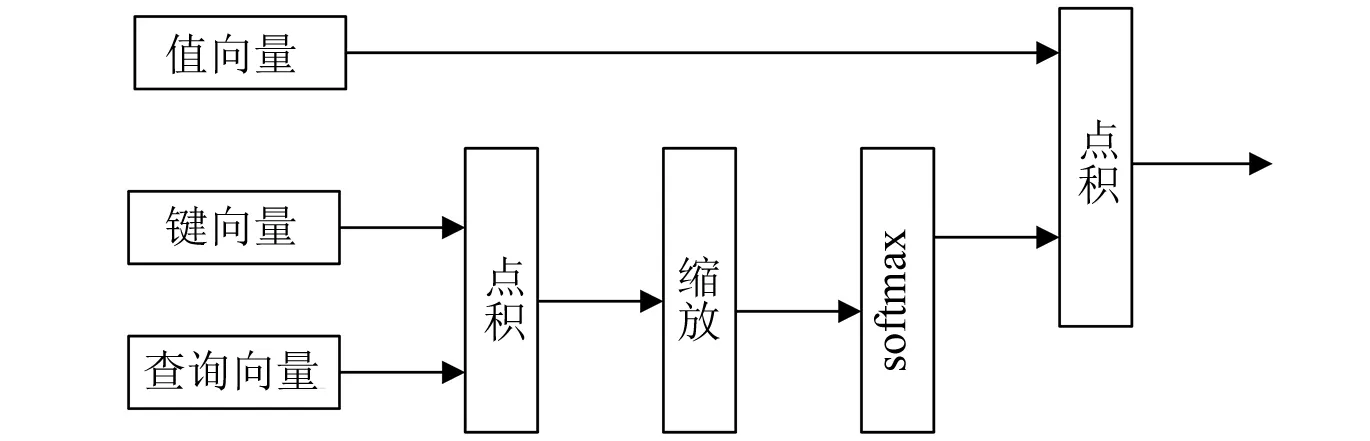
图4 缩放点积结构
具体计算步骤如下[6]。
(1) 利用样本训练过程中创建的训练矩阵(WQ,WK,WV)为每个样本X生成三个诠释向量,分别是查询向量(auery),键向量(key)与值向量(value),如式(12)所示。
(12)
(2) 对查询向量和键向量进行点积,通过softmax归一化来计算权重系数,见式(13)。
(13)
式中:d为K向量的维度。
(3) 将权重系数与值向量进行点积运算,获得对不同样本的关注度,得到自注意力机制的输出,如式(14)所示。
(14)
多头自注意力机制是多个自注意力机制的拼接,如式(15)所示。
MultiHead(Q,K,V)=Concat(h1,…,hm)·W
(15)
式中:hi为第i个自注意力;m为多头注意力个数;W为多头自注意力的权重。
3 试验结果与分析
3.1 试验平台
本文共录制了六种手势,分别是左挥、右挥、上挥、下挥、顺时针旋转和逆时针旋转。每种手势共采集了1 000个样本,其中70%用于训练集,30%用于测试集。
本文的测试环境为基于Windows10操作系统的计算机,选用的显卡型号为NVIDIA GeForce RTX 2060,在对采集数据进行处理建立数据集后利用Python3.8与Tensorflow2.3深度学习框架搭建CNN网络与Transformer网络,使用前文构建的样本集进行手势的分类与识别。
3.2 卷积神经网络验证
本文使用的CNN结构如表2所示,dropout的参数为0.5。模型训练采用的是交叉熵损失函数与Adam优化算法,初始学习率设为0.001,学习率按照指数型衰减,共训练50个epoch,样本量为256,得到如图5、图6所示的测试集准确率与损失量随迭代步数的变化曲线,准确率在40个epoch后达到收敛。
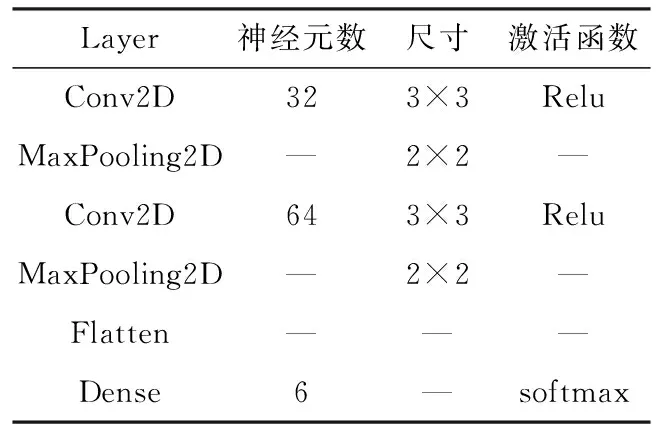
表2 CNN模型参数
3.3 Transformer模型验证
本文使用的Transformer网络共有六层编码解码层,多头参数为25,隐藏层神经元个数为512,激活函数为PRelu,dropout的参数为0.5,后接有平均池化层与全连接层。模型训练的参数与CNN相同,测试集准确率在30个epoch后近似达到收敛,具体曲线见图5。
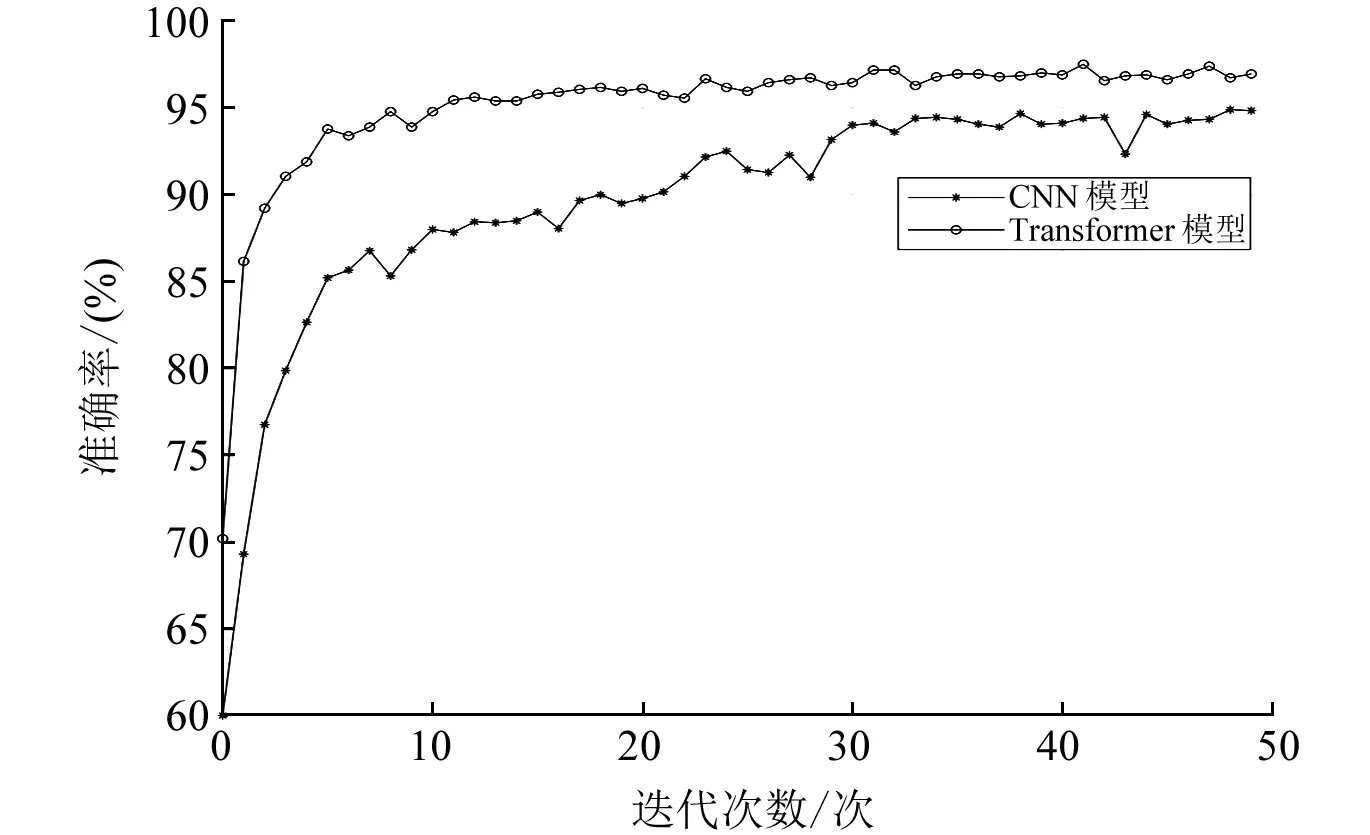
图5 不同模型训练准确率对比图
图5给出了两种模型的训练准确率对比图,图6给出了两种模型的训练损失函数值对比图。可以看到,Transformer模型在测试集上的准确率相对于传统CNN网络有了明显提升,近似收敛于97%,收敛速度有所提升,图6中的损失函数值也有所下降,验证了Transformer模型在手势识别上的有效性。
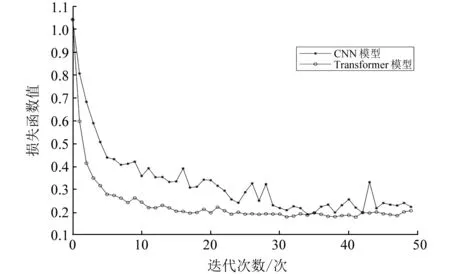
图6 不同模型训练损失函数对比图
4 结束语
本文提出了基于Transformer模型与毫米波雷达的手势识别算法,通过对FMCW毫米波雷达原理的分析设计了雷达参数,得到了手势的距离-时间、速度-时间特征,利用搭建的Transfor-mer网络进行训练,最终在测试集上的识别准确率达到了97%。
同时将Transformer网络与传统的CNN进行对比,结果验证本文采用的模型具有更短的收敛时间与更高的测试准确率,多头自注意力机制能有效学习序列动作中的全局特征,优于传统方法,具有较强的实用价值。
