基于改进粒子群算法的风机下垂控制研究
2022-11-02孙琦李岩冀宵玉刘辉
孙琦, 李岩, 冀宵玉, 刘辉
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
0 引 言
随着时代的发展,能源一直是各个国家关心的问题。煤炭、石油和天然气等传统能源对于人类的生存和发展起到了重大作用,但是其存储量十分有限且不可再生,伴随着这些能源消耗所带来的代价是环境污染。可再生能源的开发和利用是目前的主要解决方案,像风能和太阳能等新能源利用越来越广泛且正在逐渐代替传统能源。其中,风能具有存储量大和清洁等优势,使其在电力能源系统中所占据的比例越来越重[1]。
目前应用最广泛的风电机组类型主要为双馈风电机组。然而,双馈风电机组因为中间双变流器的存在使得风机的转子转速和系统频率发生解耦,导致风机响应系统频率变化的能力差[2],而且风电场为了获得最大的经济效益,会让风电机组一直工作在最大功率点跟踪状态下,因此在系统频率发生变化时,它无法像传统同步发电机一样去主动响应[3]。为了让风电机组能够参与系统的一次调频,许多学者提出了下垂控制,原理是将系统频率的偏差值引入风电机组的有功控制环节,从而实现风机的调频功能。对于下垂控制的研究大部分都采用固定下垂系数或者变下垂系数,然而所取下垂系数并不是最优系数,使得风电机组的调频效果差,系统频率稳定性不高。因此本文提出了利用改进例子群算法对下垂系数进行寻优得到最优解,使风电机组能够根据不同的变化情况找到下垂系数的最优解,从而提高风电机组的调频能力。最后通过仿真验证了所提方法的有效性。
1 风电机组下垂控制模型
1.1 最大功率点跟踪控制
为了让风电机组的风能利用率达到最大,且风电场获得最大的经济效益,通常采用最大功率点跟踪控制方式来实现,如式(1)所示。
(1)
式中:PMPPT为最大功率值;Kopt为最大功率点跟踪曲线系数;ωr为风轮转速;ρ为空气密度;R为风轮半径;Cpmax为最大风能利用系数;λopt为叶尖速比。
1.2 下垂控制
当电力系统中负荷突然增加或者减少时,系统自身频率会减小或者升高。根据同步发电机组的一次调频下垂控制特性,可以将频率的偏差值所对应的有功功率变化值,加入到风机最大功率点跟踪控制的有功功率参考值上,从而在转子侧控制形成新的有功功率参考值,这样就能让风机调整自身出力去响应系统的频率变化,这就是风机的下垂控制[4]。下垂控制框图如图1所示,公式如式(2)所示。

图1 下垂控制框图
ΔP2=-KdfΔf
(2)
式中:ΔP2为下垂控制所增加的有功功率;Kdf为下垂控制系数;Δf为频率偏差值。
2 下垂系数对调频效果的影响
构建含双馈风电机组的四机两区域模型,设定风速为10 m/s,在100 s时系统中负荷增加150 MW,然后分别设定不同的下垂系数Kdf=0、0.5、1、1.5、2.5。仿真所得到的系统频率和输出功率结果对比图如图2、图3所示。
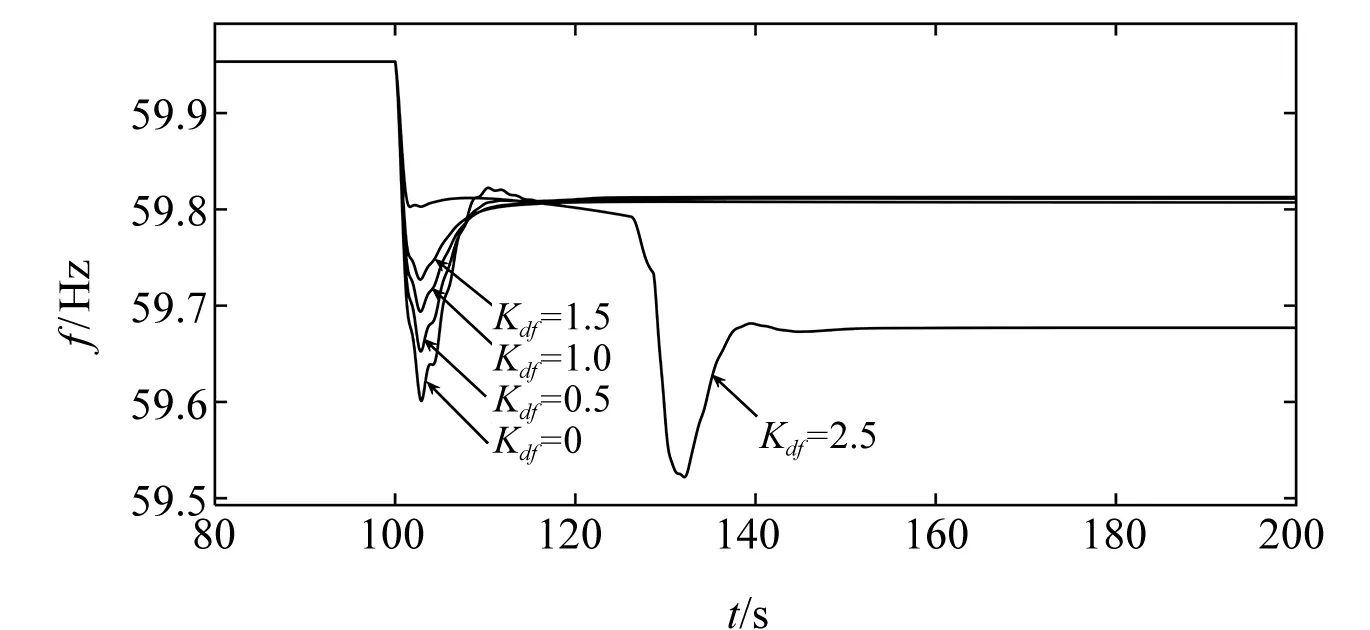
图2 不同下垂系数的频率变化图
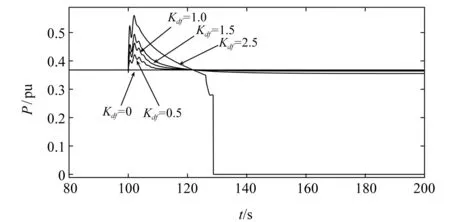
图3 不同下垂系数的风机输出功率变化图
由图2、图3分析可知:当下垂系数时,系统频率跌落的最低值达到59.601 1 Hz,此时双馈风机按照最大功率点跟踪控制,最大释放功率值保持在0.367 9 pu不变。可见当双馈型风电机组不进行调频时,系统频率跌落,风机不能通过释放转子中的动能来补充系统中所需要的功率。
当下垂系数分别设置为Kdf=0.5、1、1.5时,100 s 时系统负荷增加引起系统频率跌落。随着转速的降低,相应的转子动能进行了释放,风机的最大释放功率值分别从0.367 9 pu上升到0.421 6、0.462 3、0.493 0 pu。使系统频率跌落的最低值相比下垂控制系数Kdf=0时,分别提升了0.051 5、0.092 6、0.125 9 Hz。然而在相同的条件下,当Kdf=2.5时,虽然风机的最大释放功率值达到了0.557 4 pu,对系统频率有短时间的支撑,但风机的转子转速最低值达到0.7 pu,风机的转子低速保护开启,风机发生切机,其转子转速将增大,风机所释放的有功功率变为0,系统频率再次下降到59.521 9 Hz,比下垂控制的风机频率最低值还要低0.079 2 Hz,此时风机稳定性能下降。
综上所述,双馈风电机组在加入下垂控制之后,随着下垂系数的增大,转子所释放的动能越多,越能减小系统频率的偏差值。但是下垂系数不能无限增大,否则会使得双馈风机因触发最低转速保护而发生风机切机现象,这样会使得系统频率跌落得更深。因此需要根据实际情况来设定下垂系数。
3 基于改进粒子群算法的风机下垂系数寻优
3.1 改进粒子群算法
标准粒子群算法虽然有很好的寻优能力,但很容易陷入局部最优[5],使得陷入局部中的最优粒子无法跳出所在的范围,最终得到的最优解并不是全局的最优解[6]。标准粒子群算法中有很多的参数可以提高优化效果,其中惯性权重系数最为明显。当惯性权重系数较大时,全局搜索能力会加强;当惯性权重系数较小时,局部搜索能力会加强。因此需要平衡全局和局部的搜索能力[7],选用式(3)来决定惯性权重系数,从而根据情况找到合适的惯性权重系数。
(3)
式中:ω为惯性权重系数;ωmax、ωmin为对应惯性权重系数的最大值以及最小值;fi、favg、fmin分别为对应粒子i的适应值、所有粒子的适应度函数平均值以及最小值。改进粒子群优化算法的下垂系数寻优流程图如图4所示。
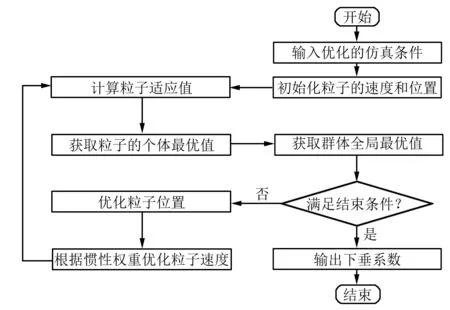
图4 改进粒子群优化算法的下垂系数寻优流程图
3.2 改进粒子群算法相关设置
针对本文采用改进粒子群算法进行下垂控制系数的寻优问题,主要的相关设置如下。
(1) 对于粒子个数,考虑到粒子的搜索空间维度只为1且Simulink仿真模型的运行速度慢,因此选取的粒子个数为10。
(2) 粒子的搜索空间设置为[0.5,3.5]。
(3) 粒子的搜索速度范围为[-1,1]。
(4) 学习因子都设置为1,惯性权重因子ωmax=0.9、ωmin=0.4。
(5)适应度函数:Φ(U)=f-min(f)。
(6)终止条件设置为最大迭代次数40。
4 仿真分析
建立含双馈风电机组的四机两区域仿真模型,仿真条件为:设置风机的输入风速为8 m/s,系统在75 s时增加100 MW的系统负荷。根据所设置的仿真条件对下垂系数进行寻优,所得到的适应度值随迭代次数的变化曲线如图5所示。
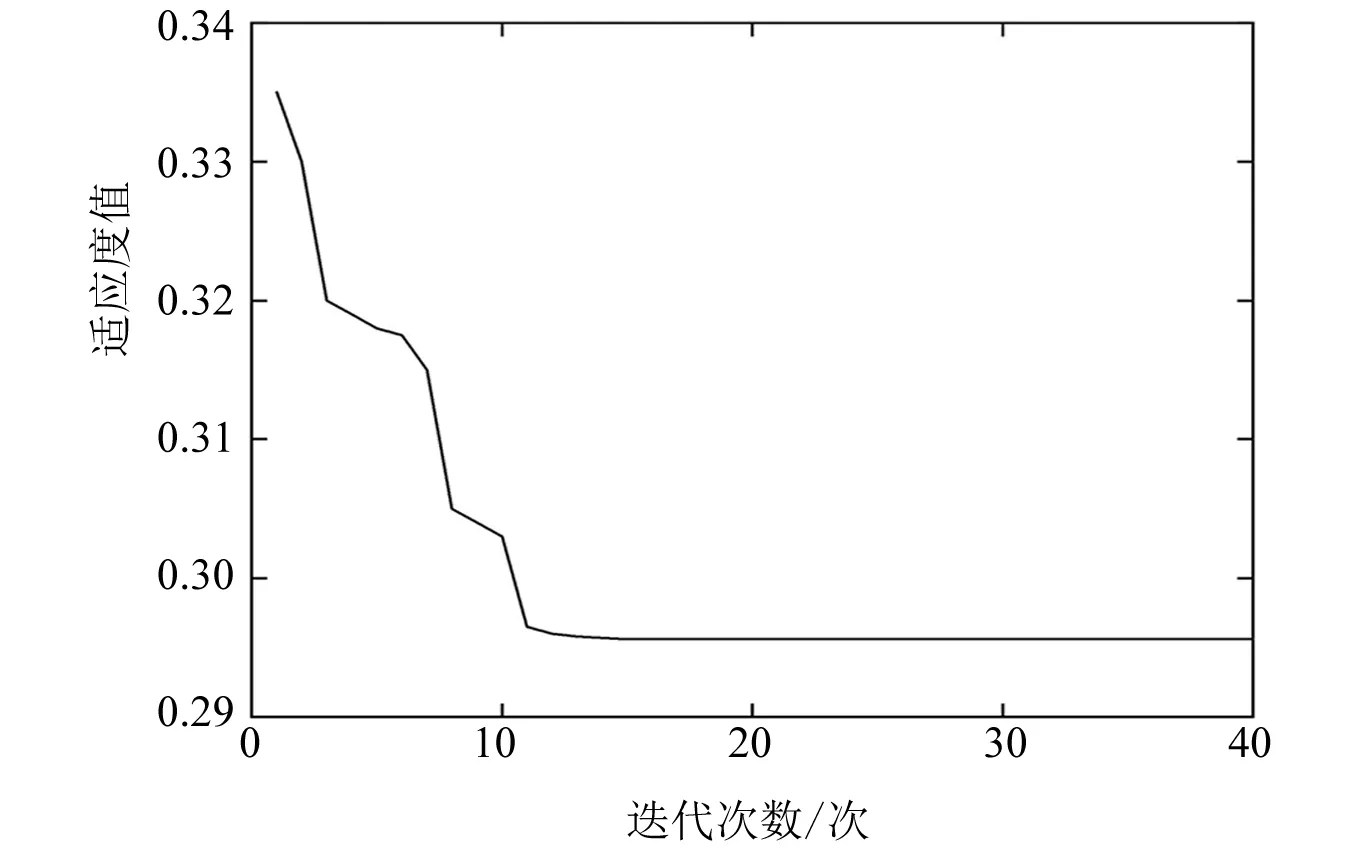
图5 适应度值随迭代次数的变化曲线
以寻优所得下垂系数让风电机组参与调频,仿真所得到的系统频率和输出功率结果对比图如图6、图7所示。

图6 所提方法下垂系数系统频率对比图

图7 所提方法下垂系数输出功率对比图
从图5可以看出,适应度值在迭代到大约11次的时候开始收敛,迭代次数达到15次之后,适应度值保持在0.295 6附近,最终改进粒子群算法寻优所对应的下垂系数为0.616。
由图6、图7分析可知,当风电机组无下垂控制时,系统频率跌落的最低值为59.649 4 Hz,此时风机按照最大功率点跟踪控制,风机的最大释放功率值保持在0.187 1 pu不变;当风机加入下垂控制,且所设置的下垂控制系数过大时,虽然风机的转子能够在系统负荷增加时,通过降低转子转速来释放相应的转子动能,但是因为风机的转子动能有限,下垂系数设置过大导致风机的转速最低保护开启,从而使得风机发生切机,最终导致系统频率相比无下垂控制的情况跌落得更深;当风机加入下垂控制,且所设置的下垂控制系数过小时,相应的转子动能释放,风机的最大释放功率值为0.207 4 pu,系统频率跌落最低值为59.668 1 Hz,比无下垂控制风机的系统频率最低值提高了0.018 7 Hz,但是因为下垂系数设置过小,风机所隐藏的动能没有充分释放,所以调频效果较差;当以改进PSO算法寻优所得到的下垂系数,让风机参与系统调频时,风机能够释放更多的转子动能,风机的最大释放功率值达到0.245 pu,系统频率跌落最低值为59.704 4 Hz,相比无下垂控制,以及下垂控制系数过小控制条件下的系统频率跌落最低值分别提高了0.055 Hz、0.036 3 Hz。由此可见,以改进PSO算法寻优所得到的下垂系数参与调频时,能有效提高系统频率的最低点,增强系统频率稳定性。
5 结束语
本文针对双馈风电机组以下垂控制参与一次调频时下垂系数影响调频效果的问题,提出以改进粒子群算法对下垂系数进行寻优,从而让风电机组能够根据不同的输入条件来寻找下垂系数的最优解,以此来提高下垂控制的调频能力。仿真结果验证了所提方式的有效性,能够提高风电机组以下垂控制参与调频的能力,增强系统频率稳定性。
