面向开集场景的辐射源个体识别
2022-11-02王春升王永民许华张悦朱丽莉
王春升,王永民,许华,张悦,朱丽莉
(空军工程大学信息与导航学院,710077,西安)
随着信息技术的迅猛发展以及通信辐射源种类数量的日益增多,无线网络安全和电子侦察面临着严峻挑战。传统的MAC地址和秘钥认证方法容易被伪造和破解,依靠信号分析方法去追踪和识别信号已无法满足复杂电磁环境下的侦察需求,特定辐射源识别(specific emitter identification,SEI)[1]通过提取辐射源信号中固有的指纹特征,再配合传统的秘钥等认证方法可以加强对非法设备的识别和身份认证,提高通信系统安全性能。另外,在电子侦察领域中,通过识别个体特征可以有效获取非合作目标信息、追踪信号位置空间、分析战场电磁态势并获取价值情报。
根据通信辐射源的工作状态,可以将信号指纹特征分为暂态特征和稳态特征。暂态特征的差异明显且容易分辨,但提取暂态特征对设备的精密性和采集条件要求高,且易受噪声干扰[2]。相较于暂态特征,稳态特征获取容易,基于稳态特征提取射频指纹的方法有广泛的研究和适用范围,如通过高阶累积量[3]、矩形积分双谱[4]、变分模态分解[5]等特征变化方法进行特征提取,并通过支持向量机(support vector machine,SVM)、聚类等分类算法进行分类。但是,这些人工设计的特征提取和分类方法复杂度较高、泛化性不强、识别率低。
随着深度学习技术的快速发展[6],很多学者将其应用于辐射源个体识别或信号识别领域。例如,利用不同的卷积神经网络(convolutional neural network,CNN)对信号的Hilbert谱图像[7]、差分星座轨迹图(differential constellation trace figure,DCTF)[8-10]、时频谱图[11-12]进行识别,这些方法都较传统方法有了大的性能提升。为了减少在信号变换中特征的丢失和模型复杂度,很多学者利用一维CNN和长短期记忆网络(long short-term memory network,LSTM)直接对基带I/Q序列数据进行特征提取和分类[13-14]。进一步地,CNN和LSTM融合的混合网络识别方法[15]、基于复数神经网络的识别方法[16]也相继被提出,这些方法利用深度学习的强大特征提取能力、自学习能力和相应的数据处理方法,使得分类性能得到了很大提升。
以往研究的通信辐射源个体识别方法大都是基于闭集环境,但实际的应用场景往往都是处于开集环境。目前,已有部分学者开始研究在开集场景下的辐射源个体识别。文献[17-18]利用基于极值理论的OpenMax[19]对雷达的高分辨距离像以及辐射源个体进行识别,相较于传统的开集识别模型有较好的性能优势。此外,将triplet loss、center loss等多种度量学习方法和深度学习结合的识别方法[20]以及基于半监督和对抗自编码器的辐射源个体开集识别方法[21-22]都取得了较好的效果。近年来,结合原型学习思想和深度神经网络的原型网络被用于小样本条件下的图像识别[23]、类增量学习[24]和开集识别[25],这些方法都取得了相较于传统CNN更好的识别性能。
目前,针对通信辐射源个体的开集别研究较少,且识别性能和鲁棒性还有待提升。文献[10]基于原型学习[24]提出残差原型网络结构,并针对信号的差分星座轨迹图进行识别,在闭集环境下取得了良好的识别性能。在此基础上,本文提出了一种开集场景下适用于一维信号的辐射源个体识别模型,该网络模型采用原型学习思想,在一维卷积神经网络中加入压缩激励(squeeze-and-excitation,SE)模块[6],利用基于原型的距离交叉熵损失(distance cross entropy,DCE)函数为每一个类别学习一个原型,通过类原型之间的距离完成分类。在此基础上,加入原型损失(prototype loss,PL)函数,在提高信号类内紧密度的同时扩增内间距离,进一步提高了模型分类能力。基于PL的作用原理,采用基于自适应距离的分类规则完成对已知目标的分类和未知目标的检测,从而完成了开集识别。对5种ZigBee设备采集的I/Q原始数据进行实验,结果表明,本文提出的模型相较于其他经典方法具有更高的识别性能。
1 开集识别和原型学习
1.1 开集识别
对于一个特定的识别问题,常用的识别方法是闭集识别,即测试集的样本类别和用于训练的样本类别相同。假定样本的类别数量为N,闭集识别所解决的问题就是完成测试集中N个类别的分类。但是,实际的应用场景中往往都是处于开集的环境,需要测试的样本中可能包含了训练集中没有出现的新类别,利用闭集识别方法所训练的模型在进行识别时会将来自未知类的测试样本识别为已知类别,从而严重影响识别精度。
开集识别为解决该问题提供了新的思路,即在对已知的N类样本进行分类识别的基础上完成对未知类目标的检测或拒绝。闭集识别和开集识别的分类模型如图1所示。在闭集识别中,所学习到的整个特征空间将会被分配给所有已知类,未知类目标只能被判定为某一个相似的已知类;在开集识别中,已知类别的特征空间是有限的,分类边界在对已知类别进行分类的同时可识别出未知类别,并将所有未知类别的样本划分为一类。

图1 闭集识别和开集识别模型Fig.1 Recognition models for closed set and open set
1.2 原型学习
原型学习通过特定的学习方法为每个类别计算出一个或多个原型表示aij,其中i∈{1,2,…,N}表示样本中共有N个类别,j∈{1,2,…,M}表示每个类中有M个原型[24]。在分类识别任务中,可以利用神经网络强大的特征提取能力来提取数据特征,并构建每一个类原型,神经网络作为特征提取器可表示为f(x;θ),x和θ分别表示网络的原始输入和参数[10]。以往的CNN模型在分类的时候使用softmax函数对全连接层的输出进行归一化,以最大概率值对输入样本x进行判定和分类。分类依据为
(1)
式中:y∈{1,2,…,N};p(y|x)表示样本x属于类别y的概率;δi表示第i类对应的网络输出值。利用原型学习进行分类时,网络可为每个类学习一个原型。对于任意样本,可以将它划入到距离最近的原型所属的类别。该过程可以表示为
(2)
式中gi(x)是类别i的分类函数,表示为
(3)
其中f(x;θ)和原型ai可以联合学习。在学习过程中,不断将某一类原型推向该类的样本特征,而其他类的原型远离该类样本特征。原型学习将分类问题转化为在特征向空间中的最近邻问题,结合神经网络的特征提取优势,可以有效缓解过拟合,提高泛化性能和识别性能。
2 辐射源个体识别模型
2.1 模型框架
开集场景下基于原型网络的辐射源个体识别模型是利用一维卷积神经网络为基础结构,结合原型学习方法和SE模块对预处理的I/Q信号进行识别,并利用自适应距离分类规则完成分类预测。
开集场景下基于原型网络的辐射源个体识别模型如图2所示,主要分为3个模块。第1个模块为数据处理模块,接收端接收信号后,首先对其进行高采样率采样,然后按照样本长度对数据进行功率归一化、切片和加噪等操作,最后按预设比例划分训练集和测试集。第2个模块为特征提取和参数更新模块。将处理好的I/Q数据送入一维CNN,对于该网络模型,给定输入x,通过神经网络特征提取器f(x;θ)获得它的抽象特征表示。在训练阶段,通过最小化损失函数和神经网络的反向传播算法同时更新网络参数和原型,更高效地训练整个网络。第3个模块为分类模块,在训练阶段,将训练样本提取到的抽象特征与所有原型进行匹配,根据欧氏距离将其分类到最近原型所属的类别。在测试阶段,将测试样本提取到的抽象特征与所有已训练好的原型进行匹配,根据自适应距离分类规则将测试样本分类为已知类别的某一类或未知类别。

图2 开集场景下基于原型网络的辐射源个体识别模型Fig.2 Specific emitter identification model based on prototype network for open set scenes
2.2 网络结构设计
开集识别网络结构如图3所示。本文直接对序列数据进行处理,复杂度较低,故设计的网络结构以较为简单的一维卷积神经网络为基础。网络层数共有4层,每一层的卷积核数分别为32、64、128、256。在每一个卷积层后添加内核为2的最大池化层来降低模型的复杂度和过拟合程度,通过4层的网络使得最后的输出样本维度降到一个较低的值,以便充分提取数据的深层特征。

图3 开集识别网络结构Fig.3 Network structure of open set recognition
每个卷积层的卷积核大小为1×9,使用较大的卷积核能够充分提取序列数据中的时序信息。在每一次卷积和池化操作后加入SE模块,通过调整各通道的权重进一步提高识别准确率。在最后一个卷积层中加入Dropout层,以缓解模型在训练中出现的过拟合现象。在卷积操作中对每一个样本数据的边缘补0,保证充分提取该样本的特征,并确保卷积后得到的样本长度不变。
在卷积层后,采用PReLU激活函数。PReLU激活函数在负值时的斜率是在0~1之间可学习的。在神经网络中,初始化权重和权重更新时,都有可能出现权重为负值的情况,使用PReLU激活函数,保证了在激活函数输入特征为负值的时候其输出值不为全0,能够更全面地保留网络提取的特征,提升识别性能。在所有卷积操作完成后,采用自适应平均池化,输出大小维度为1×1。最后经过全连接层,输出2维特征,输出特征通过DCE损失和PL损失计算特征到原型的欧氏距离,同时更新网络参数和原型ai。
网络中加入的SE模块采用了注意力机制,其核心思想是通过不断学习来自动获取在卷积过程中每个特征通道的重要程度,依据重要程度来调整各通道的权重,在权重的作用下可提高有效通道特征的影响,抑制作用较小的通道特征,进而提高网络的识别性能。一维SE模型如图4所示,输入数据X=(u1,u2,…,uC′),经过卷积操作后提取的特征为U=(u1,u2,…,uC),其中C和C′代表通道维度,L和L′代表每一个通道的特征维度。为了适应一维数据处理,将SE模块中的二维结构改为一维结构。该模块总共分为3个步骤。第1步,进行Squeeze操作。保留通道数不变,将时间序列数据中的C×L维特征经过一维自适应平均池化,变成C×1维特征,使其具有全局感受野。该过程可表示为
(4)
式中:Fsq(·)代表Squeeze操作;uc∈RL代表操作前的特征分布;zc代表z的第c个分量,z∈RC代表Fsq(·)操作后的特征分布;uc(i)代表U中第c个通道的第i个分量。

图4 一维SE模型Fig.4 One-dimensional SE model
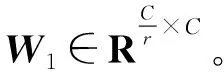
s=Fex(z,W)=σ(g(z,W))=σ(W2δ(W1z))
(5)
式中:δ代表ReLU函数;σ代表Sigmoid函数;Fex(·,W)代表Excitation操作。

(6)
式中Fscale(·,·)代表特征重标定操作。
2.3 自适应距离分类规则
在闭集场景下,对已知类目标的分类可以基于式(2)、(3)完成。在开集场景下,对已知目标的分类和未知类目标的检测可以在原型网络的基础上使用基于距离的拒绝规则。
在式(3)中,gi(x)代表样本x属于类别i的匹配程度,即样本x到类别i的距离。在测试时,如果样本x到类别i的最近距离大于阈值ω,即
(7)
则代表该样本x与已知类别i的原型ai匹配程度很低,可判定该样本为未知类别[25]。式中f(x;θ)代表样本x的深度特征。基于gi(x)的定义,则有
maxgi(x)<-ω
(8)
式(8)代表样本x属于类别i的最大匹配程度小于某一个阈值,等价于式(7)。
然而,在基于距离的拒绝规则中,阈值ω难以设定。选取不同网络结构、网络深度,不同信噪比下的识别信号或者不同的λ进行训练拟合时,都会导致每一个类出现不同的样本分布,而不同的样本分布会导致每一个类原型之间的距离不同,且每一个类的样本到该类别所属原型的距离分布也不同。因此,使用固定的阈值ω会使得拒绝检测不具有鲁棒性,且阈值ω也难以确定。
图5是不同信噪比和不同类别样本下的特征分布对比。可以看出,经过训练后,不同信噪比下已知类的样本以及类原型分布不同。图中,d1≠d′1,d2≠d′2,因此用来判定样本属于某一类原型的距离阈值ω就不同,这就给ω的设定带来了困难。

(a)10 dB下的样本特征分布
基于此,本文提出了基于自适应距离的分类规则。在该规则中,距离阈值ω是可学习的,在训练期间,根据每一个类别样本的分布情况,可以自动调整ω,得到一个更具鲁棒性的ω。具体算法如下:在训练期间,根据标签信息得到每一个预测正确的样本x,通过CNN网络提取到特征f(x;θ),计算特征f(x;θ)到样本x对应原型的距离。训练完成后,得到所有类的原型以及正确预测样本x所提取的特征f(x;θ)到对应原型的距离分布D,表示为
D={dxi|x=1,2,…,T;i=1,2,…,N}
(9)
式中:T代表训练集中每个类别的样本数量;N代表类别数量;dxi代表样本x到对应原型ai的距离。在测试时,由于测试样本中未知样本的空间分布情况未知,它可能在不同的网络模型或数据集下出现不同的位置分布。对于每一个测试样本,首先计算该测试样本到每一个原型ai的距离,找到最近距离所对应的类别i,计算式为
(10)
之后,根据所找到的类别i以及该类样本特征到类原型ai的距离分布,得到最大距离分布值di=maxdxi。将该距离分布值di作为类别i的距离阈值ωi。如果测试样本到最近原型的距离小于该类原型的阈值ωi,则判定为该类别,否则判定为未知类样本。判别式表示为
(11)
2.4 损失函数定义和优化方法
2.4.1 DCE损失
在原型网络结构中,用距离来衡量样本和原型之间的相似性[23]。因此,样本(x,y)与原型ai之间的距离可以衡量其属于原型的概率,其中,x为样本,y为样本对应的标签。基于文献[24]和[10]的分析,可以将DCE损失定义为
(12)
式中:A={ai|i=1,2,…,N}代表类原型集合;q(y)是样本标签的分布;p(y|x)表示样本x属于类别y的概率;K为一个批次的样本数量。
2.4.2 PL损失
为了进一步提高网络的识别性能,同时完成开集识别任务,可以在训练期间通过PL损失函数[24]缩小类内样本特征间的距离,继而以提高类内紧密度的方式增加类间距离。同时,通过该损失函数的约束,在缩小已知类样本特征空间的基础上扩大了未知类的空间分布,更有利于对未知类目标的检测和拒绝。PL损失定义为
(13)
式中ay为y类所属原型。最小化PL((x,y);θ,A)可以缩小各类样本特征到所属原型的距离。
2.4.3 联合损失
根据以上分析,可以将DCE损失和PL损失相结合来训练模型。联合损失可以定义为
(14)
式中λ是控制PL损失权重的超参数。通过结合DCE损失和PL损失,可进一步提高网络的分类准确率和鲁棒性。另外,PL损失作为正则化项和对已知类样本空间的约束函数,既有助于完成开集识别任务,也可以防止模型的过拟合,增加泛化性能。通过式(14)分析得到,λ太小则类内分布空间不够紧密,难以达到更优的识别性能。λ太大也会过度提高样本空间的紧密度,增加过拟合程度,降低闭集和开集识别的分类性能。
2.4.4 优化方法
采用自适应梯度下降(Adma)进行优化,优化目标为最小化联合损失L((x,y);θ,A),每批训练样本数为64,学习率初始值为0.000 5。迭代数选择为40,每迭代10次后学习率降低50%。
2.5 训练和测试方法
在训练时,首先根据特征维度和类别数目对每一类别构造原型,并对原型进行初始化。输入样本经过网络提取特征后,计算与各个类原型的距离,根据距离再计算出DCE损失和PL损失。最后,联合DCE和PL损失进行端到端训练和网络优化,同时更新网络参数和原型ai。
在测试时,将输入信号的抽象特征与所有类别的原型进行比较,根据自适应距离分类规则将测试样本分类为已知类别的某一类或未知类别。
3 实验与结果分析
3.1 实验平台和数据预处理
3.1.1 实验平台
本文实验基于Python下的Pytorch深度学习框架,所使用的硬件平台中CPU为 AMD Ryzen 7 5800H,GPU为 NVDIA GeForce RTX3070。
3.1.2 数据预处理
实验所用数据集来自5种ZigBee设备的实采信号[8],采样率为107s-1。信号调制方式为OQPSK(offset quadrature phase-shift keying),遵循IEEE 802.15.4标准,信号接收设备为Ettus Research N210 USRP。每一类设备有5段信号,每段信号分为9个小的帧段,每个帧段约为40 000个样本。将所有采集到的信号进行预处理,首先对信号进行功率归一化,消除在实际采集数据时因信号功率不同带来的影响,然后对信号进行切片处理、加高斯噪声。
在闭集实验中,随机选取每一类设备的4段信号为训练集,第5段信号为测试集。在开集实验中,选取其中的3类设备,每一类设备选取4段信号作为训练集,而测试集选取5类设备的第5段信号。
3.2 不同参数下的识别性能对比
3.2.1 不同样本长度下的性能对比
采用控制变量法选取最优识别性能下的参数。图6显示了在闭集环境下,信噪比在-10~6 dB之间变化时不同样本长度下的识别准确率。可以看出,对于序列信号:当样本长度较小时,网络难以提取到样本所包含的指纹特征,识别精度较低;当样本长度逐渐变大时,样本所包含的指纹特征更丰富,识别精度逐渐提高。但是,当样本长度过大时,识别精度会下降。原因是随着样本长度的增大,用于识别的指纹特征已经达到饱和,识别精度变化就不明显。另外,随着样本长度的增大,用于训练和测试的样本减少,测试精度就会受到较大影响。在高信噪比的情况下,模型能够较容易识别不同类信号,识别精度在不同样本长度下的变化不明显;在低信噪比的情况下,识别精度对参数的变化较敏感,所以在不同样本长度下的变化较大。综合实验结果来看,选取样本长度为800个采样点进行后续实验。

图6 不同样本长度下的识别准确率对比Fig.6 Comparison of recognition rate with different sample lengths
3.2.2 不同λ下的性能对比
选取样本长度为800,对比在闭集和开集环境下信噪比在-10~6 dB之间变化时不同λ对应的测试精度。闭集和开集环境下的识别准确率如图7所示。可以看出,实验结果验证了PL损失的理论分析。λ决定了每一个类别的聚集程度,进而影响了类别之间的距离分布,使得不同λ下的识别性能也不同。通过实验得出,当λ为0.05左右时,识别性能最好。λ取值从0开始增大时,每一类特征的类内紧密度会逐渐增高,继而扩增了类间距离,既提高了对已知样本分类能力,也增强了对未知目标的检测和拒绝能力。随着λ的进一步增大,识别性能趋于稳定。当λ过大时,PL损失对样本空间的约束就越大,就会将训练集的每一类样本空间过度缩小到类原型的附近,加重了过拟合现象。当输入测试样本时,测试集的样本空间分布会大于训练收敛后的样本空间分布,在通过类原型之间的距离进行判别时就会影响识别性能。同样地,在低信噪比下变化更明显,因此选择合适的λ对识别性能至关重要。另外,PL损失对开集识别的作用更明显,其作用原理也更适合对未知类目标的检测。

(a)对闭集识别准确率的影响
图8为开集识别下不同λ所对应的全连接层2维输入特征分布。可以看出,在DCE损失的作用下,可以完成对已知类的分类和对未知目标的检测,但从样本的分布来看,准确率和稳定性还不够高。在加入PL损失后,通过提高类内紧密度的方式扩大未知空间的分布,同时使得已知类样本和未知类样本在特征空间更加分离,继而提高了开集识别准确率和鲁棒性。
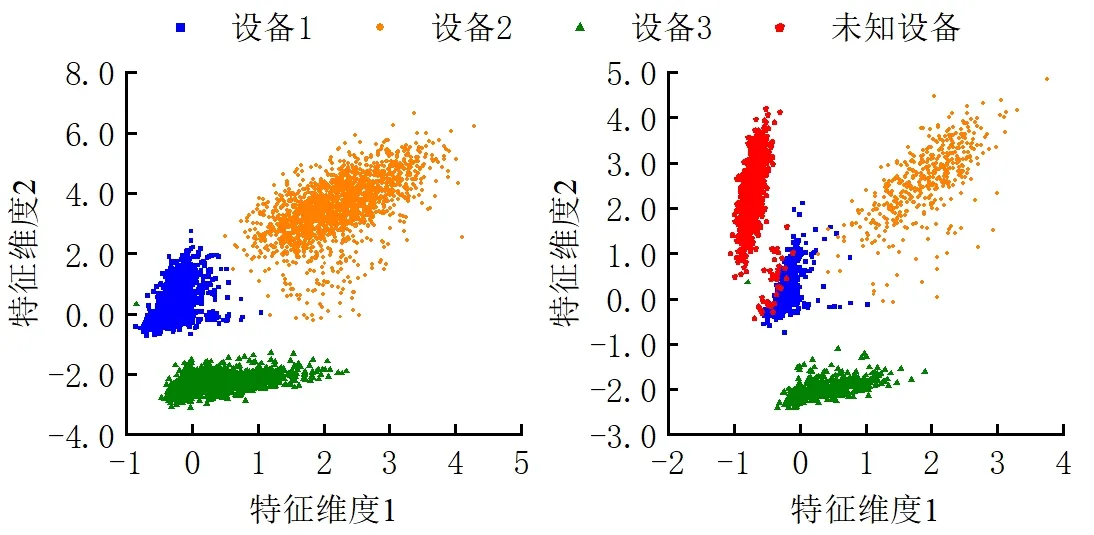
(a)λ=0时的训练特征分布 (b)λ=0时的测试特征分布
3.3 不同模型的识别性能对比
3.3.1 闭集环境下的识别性能对比
参照之前的实验结果,选取信号样本长度为800,λ为0.05,信噪比变化范围为-10~10 dB,将本文提出的原型网络模型PN-SE与未加入SE模块的原型网络PN和未加入原型学习的一维卷积神经网络CNN-SE进行识别性能对比。为了进一步说明本文模型相较于其它模型的性能优势,同时将本文模型与DCTF-CNN[8]、PACGAN[9]、LSTM-CNN[15]这3种不同网络模型进行对比,以上几种模型都是针对ZigBee设备进行识别的。在对比实验中,使用本文数据集,按照相应的数据处理方式进行处理。
闭集环境下不同模型的识别准确率对比如图9所示。可以看出:引入原型学习思想,采用联合损失函数后可以在同等网络结构下增强模型的识别性能。在加入SE模块后,通过引入注意力机制改变了通道权重,可以提高原型网络的识别准确率。在较低信噪比下,本文提出的模型有较大的性能优势。当信噪比大于0 dB时,本文模型识别精度可达到95%以上;当信噪比大于6 dB时,本文模型识别精度可达到99%以上。另外,通过实验和分析得到,将信号转化成DCTF图像会丢失掉一些细微特征,导致在低信噪比下识别准确率不佳。
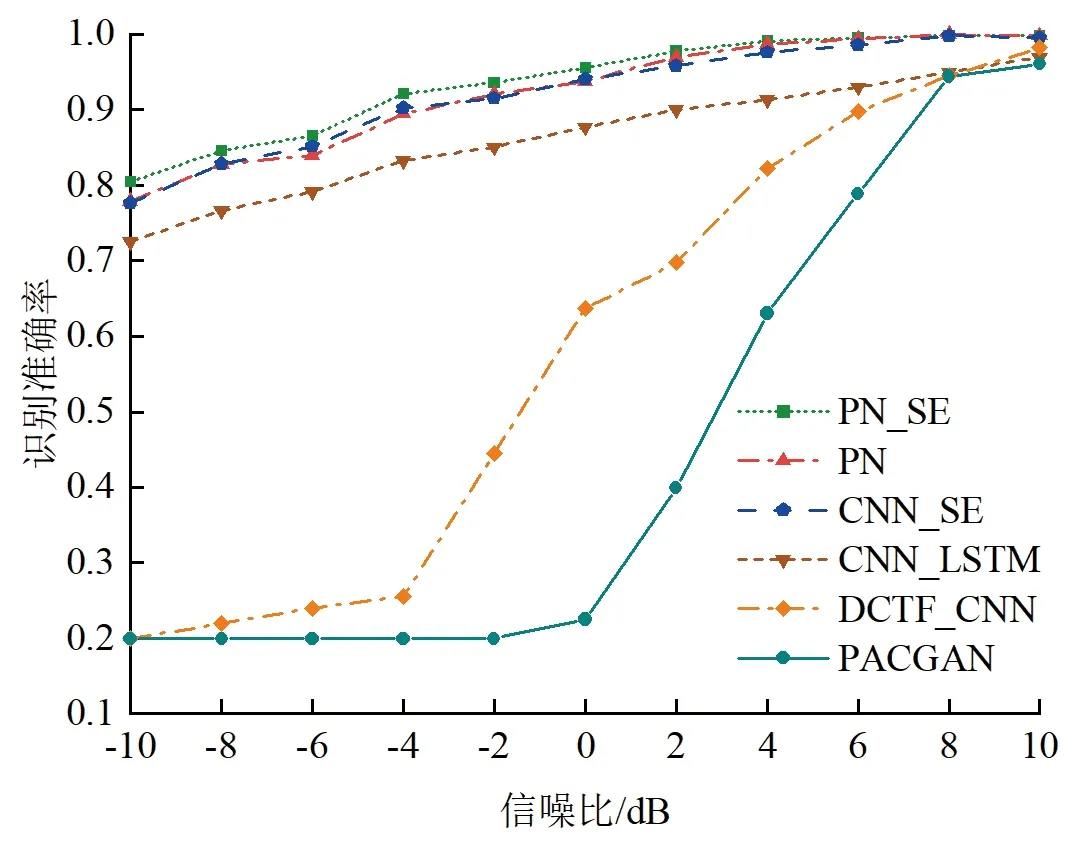
图9 闭集环境下不同模型的识别准确率对比Fig.9 Comparison of recognition rate with different models in close set scenes
3.3.2 开集环境的识别性能对比
为了说明本文模型PN-SE-Open在开集识别中的优越性能,首先将本文模型与未加入SE模块的PN-Open模型进行对比,然后将本文模型与基于OpenMax[7-18]的开集识别模型进行对比,最后再对比本文模型在开集环境和闭集环境下的性能差别,闭集环境下的识别曲线为PN-SE-Close。所有模型均采用本文所用数据集,对比结果如图10所示。
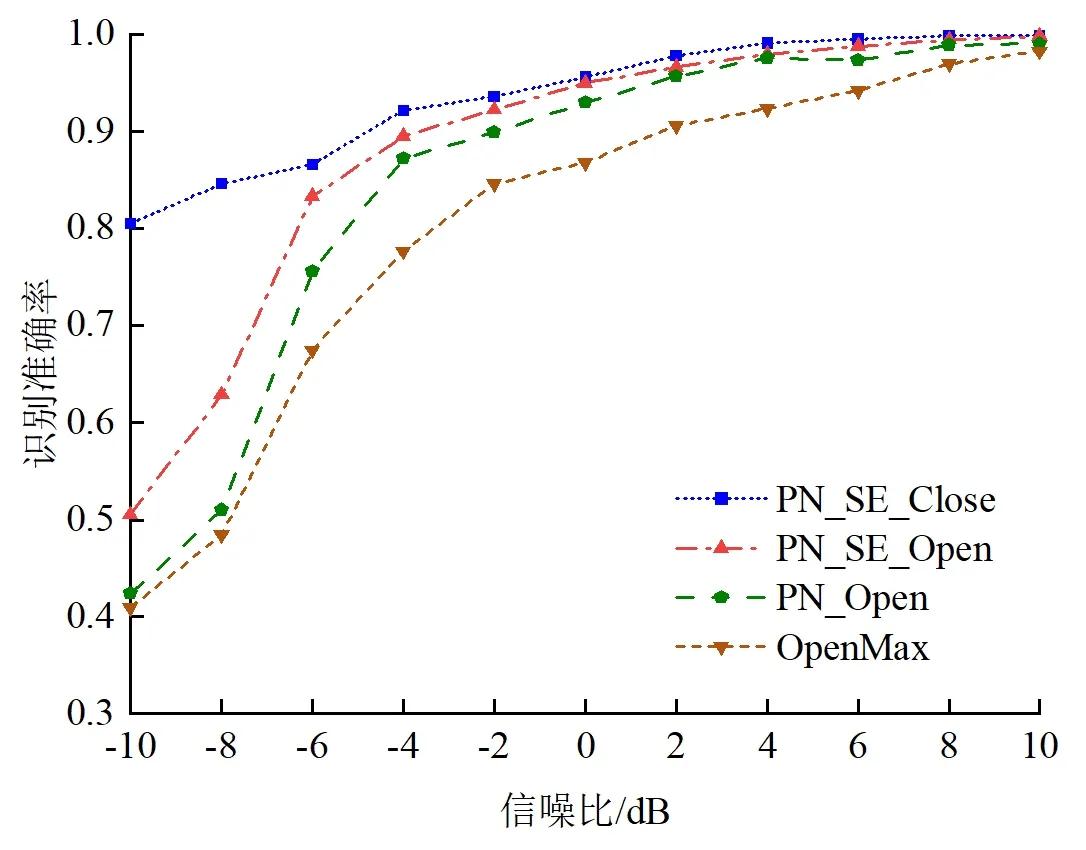
图10 不同模型的识别准确率对比Fig.10 Comparison of recognition rate with different models
可以看出,本文模型在开集场景下相较于其他模型具有更好的识别性能,当信噪比为0 dB以上时,可达到95%的识别准确率。在加入SE模块后,尤其是在低信噪比下,开集识别的性能有较大提升。另外,当信噪比为-6 dB以上时,开集识别准确率和闭集识别准确率相当,这也充分说明了本文模型在不同识别场景下均可以达到良好的识别性能。
在-6、0、6 dB下,开集识别的混淆矩阵如图11所示。可以看出,第1类和第2类设备容易混淆,第3类较为独立。即使在较低信噪比下,第4类和第5类设备的信号作为未知类目标也能够很好的被检测和拒绝。

(a)-6 dB下的混淆矩阵
4 结 论
本文在原型网络模型下,通过自适应距离分类规则实现了ZigBee设备个体的开集识别。在一维卷积神经网络中加入SE 模块,通过调整通道权重加强分类能力;结合DCE损失和PL损失对网络的参数和原型进行联合训练,同时更新网络参数和原型,有效地提高了网络的识别性能;通过引入PL损失,以提高类内紧密度的方式扩大了类间距离,进一步增强了模型的分类能力;通过自适应距离分类规则,完成了开集场景下的辐射源个体识别,免去了人工阈值的设定。通过实验对比可知,本文提出的网络模型在闭集环境和开集环境下都具有更高的识别精度和泛化性。后续研究应着重改进分类规则,提高基于原型的距离分类规则的鲁棒性,同时应加强对未知类样本空间的建模和分析。
