巧思维切入,妙视角拓展
——一道向量题的深入学习
2022-11-02黄水华
黄水华
(江苏省江阴市祝塘中学,江苏江阴,214415)
1 问题呈现

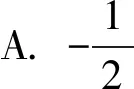
此题以三角形为问题背景,结合三角形的两边与夹角的已知条件合理创设情境,通过相应边上的动点与对应三角形的两顶点所对应的向量的数量积的构建,来确定对应的最值问题.问题比较常规,难度中等,巧妙设置“动点”,通过动静结合,“动”中取“静”,合理求解对应数量积的最值.
2 解题思维
思维视角一:基底思维
方法1:(数量积法)
解析:设MC=t∈[0,3],
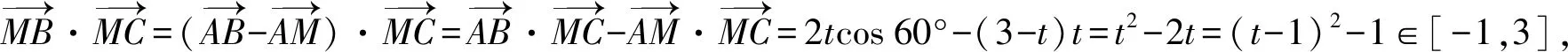
解后反思:随着线段长度的变化引入对应的参数,结合平面向量的相关知识转化为含参的二次函数的最值或取值范围问题,借助配方处理并利用二次函数的图象与性质来确定数量积的取值范围.抓住平面向量的基底思维,结合平面向量的线性运算是解决平面向量问题中最常用的基本思维.
思维视角二:几何思维
方法2:(相交弦定理法)

解析:如图所示,过点B作BD⊥AC,垂足为D,可得AD=ABcos 60°=1,则有DC=2,

过点C作CE⊥BM,垂足为E,则知B、C、E、D四点共圆,结合圆的相交弦定理,可得MB×ME=MD×MC,

解后反思:根据题目条件合理构建平面几何图形,结合所求结论确定动点的位置,通过垂直的构建,结合四点共圆合理构建圆,利用圆的相交弦定理以及平面向量的投影加以转化与应用,利用基本不等式的应用来确定对应的最值问题.抓住平面向量的几何思维,利用三角形、圆以及投影等几何要素来合理转化与巧妙应用.
方法3:(极化恒等式法)
解析:由AB=2,AC=3,∠BAC=60°,

如图所示,取BC的中点D,连接MD,过点D作DE⊥AC,垂足为E,

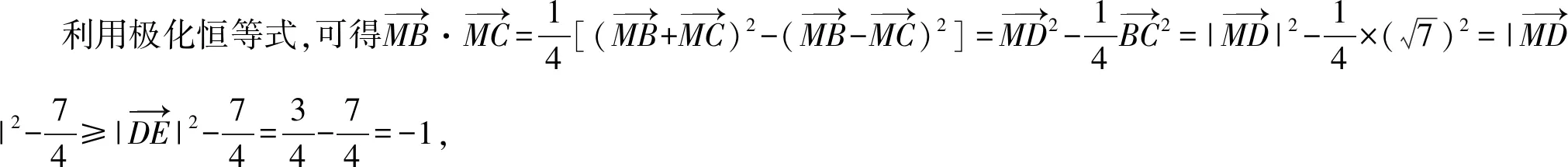

解后反思:根据题目条件加以合理构建平面几何图形,借助平面几何的直观,通过解三角形思维的应用以及直角三角形的性质特征,利用极化恒等式加以转化,数形结合来确定对应数量积的最小值,实现问题的直观转化与数形结合.抓住平面向量的几何思维,结合平面几何图形的直观形象来数形结合,合理推理与巧妙应用.
思维视角三:解三角形思维
方法4:(解三角形法)
解析:设MC=t∈[0,3],
由AB=2,AC=3,∠BAC=60°,
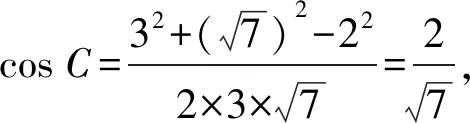

解后反思:随着线段长度的变化引入对应的参数,结合解三角形中的余弦定理的应用求解对应的边长与角的余弦值,进而确定对应边的表达式,综合余弦定理的向量式加以转化,构建含参的二次函数的最值或取值范围问题,结合配方处理并利用二次函数的图象与性质来确定取值范围.抓住平面向量的解三角形思维,从三角形视角切入来分析与求解,回归平面向量相关概念的几何意义来转化与应用.
思维视角四:坐标思维
方法5:(坐标法)
解析:以顶点A为坐标原点,AC所在直线为x轴建立平面直角坐标系xAy,




解后反思:将对应的三角形放入平面直角坐标系中去,结合对应点坐标的确定与设置,将几何问题代数化,借助平面向量的坐标性质与运算加以转化,进而确定一个含参的二次函数问题,借助配方法的巧妙处理,利用二次函数的图象与性质来转化与应用.抓住平面向量的坐标思维,结合平面向量的坐标表示与坐标运算,是代数法解决平面向量问题中一种基本技巧策略.
3 变式拓展
探究1:保持题目条件,改变所求平面向量的数量积的最值为取值范围,使得问题更加全面,实现问题的进一步拓展与提升.


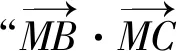
探究2:保持题目条件,进一步加以拓展,求解动点到三角形的三个顶点中任意两个顶点所对应的向量的数量积之和的取值范围问题,使得问题变得更加复杂多样.
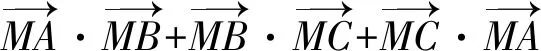

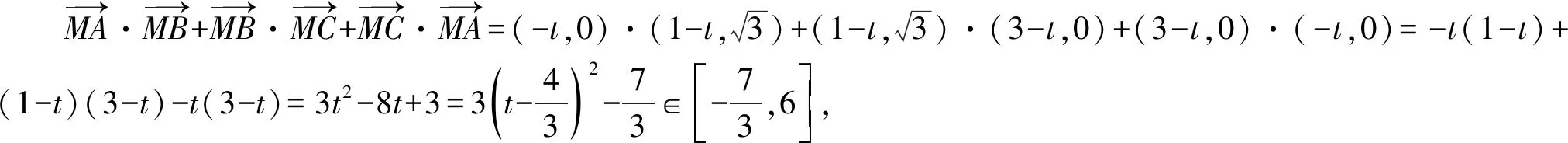
点评:这里也可以设置求解对应平面向量的数量积和式的最小值(或最大值)问题.通过坐标法处理最为合理有效,也是坐标思维的进一步综合应用.
探究3:在变式2的基础上,将动点M在规定的边上运动,拓展到在三角形所在的平面上运动,进而得到以下对应的变式问题.
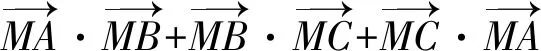
解析:以顶点A为坐标原点,AC所在直线为x轴建立平面直角坐标系xAy,




点评:对动点不加以限制.改变其他的限制变化情况,都可以合理创设新的变式问题.解决此问题可以巧妙借助坐标思维加以分析与处理.也可以尝试其他思维方法.
4 教学启示
4.1 思维视角总结,方法技巧归纳
解决平面向量时,经常利用基底、几何与坐标这几个常见的思维方式进行切入,有时还有解三角形思维、三角函数思维以及特殊思维等,从平面向量的线性运算、坐标运算或三角函数运算等来进行数学运算,或从平面几何图象的直观形象来数形结合,充分展示平面向量同时兼备“数”的性质与“形”的特征这一双重性质.
4.2 “一题多解”发散,“一题多变”升华
对平面向量问题的“一题多解”,进一步发散思维,融合数学基础知识与基本技能,形成稳定的知识架构;而借助“一题多变”,进一步升华能力,真正达到会解、会用、会拓展等.在此层面上,进一步实现“一题多得”的良好效果.
