基于乌鸦算法的水轮机调速器参数优化研究
2022-11-02屈靖杰
屈靖杰
(国能大渡河检修安装有限公司,四川 成都 610000)
目前我国水轮机调节系统大多采用PID控制,它对水电站电能质量有重要影响。调速器的比例(P)、积分(I)、微分(D)三种参数的设定决定了调节系统的调节性能,因此优化PID参数是改善系统调节能力的关键。
水轮机PID调速器的方法有:传统的粒子群算法(PSO)、扰动观察法(P&O)、遗传算法(GA)等等,它们对水轮机调速器参数优化有积极的推动作用,但这些传统算法都存在普遍存在收敛速度慢、精度低和易陷入局部最优等缺陷,同时算法存在调节参数多、算法复杂、振荡幅度大的问题。学者们对传统算法的不足进行改进,提出了仿生智能优化算法。
乌鸦算法(Crow Search Algorithm, CSA)是新型智能算法,它模拟乌鸦觅食窃取与反窃取行为。与相较传统算法,CSA算法结构简单,收敛速度快,精度高,有效避免陷入局部。目前在工程设计、图像处理等优化问题中运用。
1 CSA算法
乌鸦会把剩余的食物藏起来,藏匿位置称为记忆值;当窃取其他乌鸦食物时,而被窃取的乌鸦则会有一定的感知概率 ,会改变空间方位来保护食物。
CSA算法过程如下:首先生成大小为N的乌鸦群体:

(1)乌鸦j跟踪乌鸦i,乌鸦i新位置:

(2)乌鸦j知道乌鸦i在跟踪它,在空间随机移动欺骗乌鸦i。
结合情况1、2,更新后的乌鸦位置为:

式中:rj是[0 1]之间的随机数;APj,iter为乌鸦j在第ter次迭代后的感知概率AP;fli,iter是第i只乌鸦在iter次循环时的飞行距离。
1.1 算法步骤
步骤1:初始化参数N,fl、AP、iter;
步骤2:通过计算适应度函数,选出最优位置k*;
步骤3:随机选取乌鸦j,如果ri≥AP,则乌鸦i更新位置:
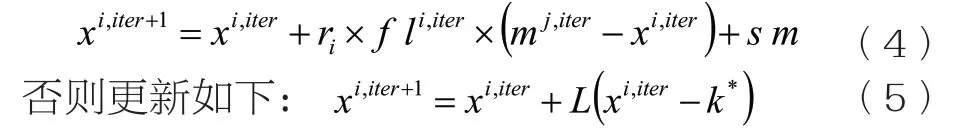
步骤4:判断新位置的可行性;
步骤5:重新计算适应度函数。比较前后适应度值更新乌鸦记忆;
步骤6:判断迭代次数是否满足要求。若满足,输出最优解;否则重新更新位置。
改进乌鸦算法流程图如图1所示。
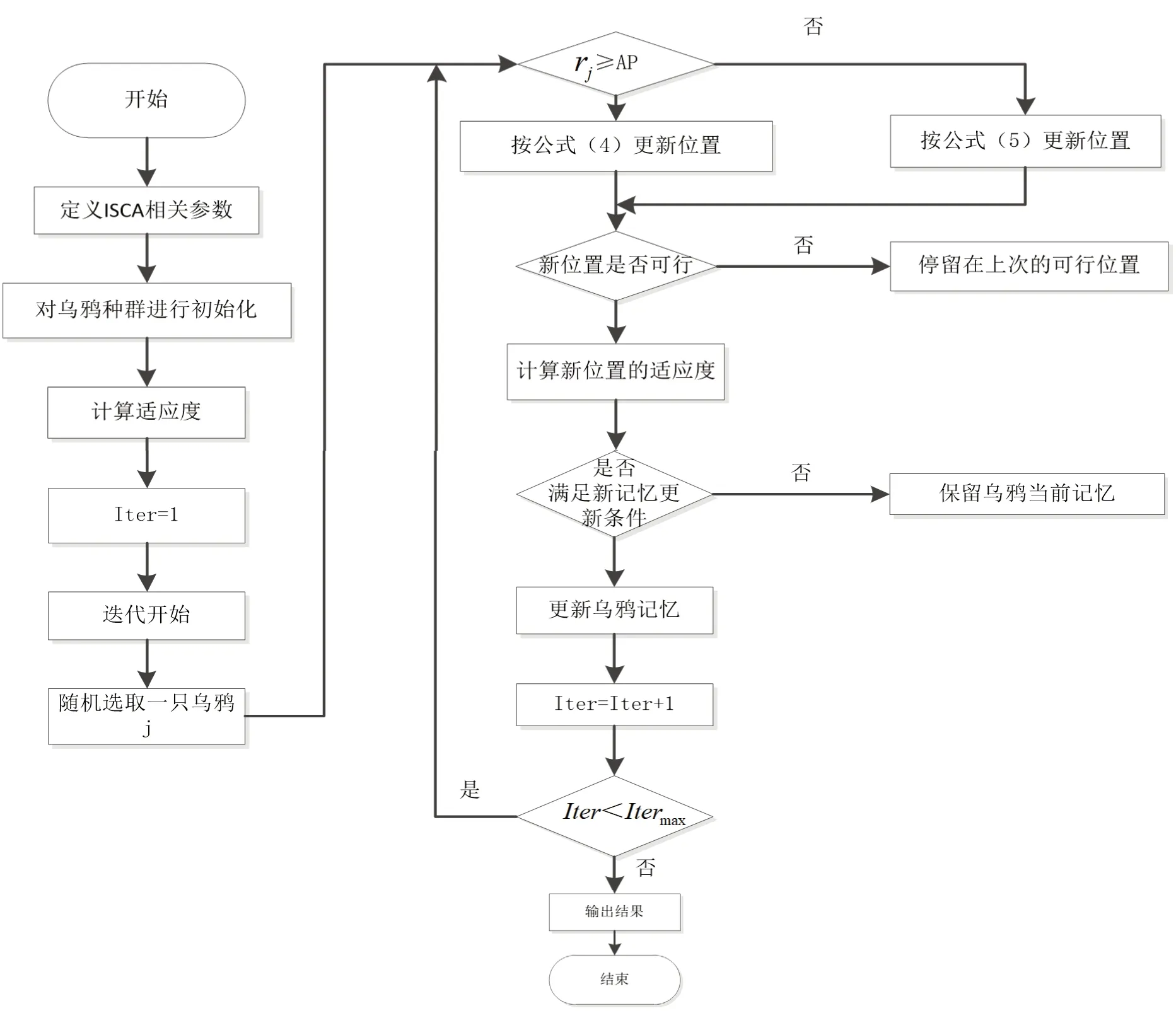
图1 基于乌鸦算法的水轮机调速器参数优化的流程图
2 基于CSA算法的水轮机PID调速器控制
2.1 典型水轮机调速器
典水轮机调节系统是由调节器、随动系统、水轮机及引水系统、机组等部分组成。结构图如2所示。

图2 水轮机调节系统模型
图中:Ty为接力器反应时间常数;ey为水轮机力矩对导叶开度的传递函数;eqh为水轮机流量对水头的传递函数;eh水轮机力矩对水头的传递函数;eqh为水轮机流量对导叶开度的传递函数;Tw为水流惯性时间常数;Ta为机组惯性时间常数;Tb为电网惯性时间常数;en为综合自调节系数;xc为频率给定值输入;x为频率输出;mg0为负荷输入。
调速系统分为连续系统与离散系统,调速器一般采用PID控制规律。决定了系统的稳定性,决定了系统的扰动抑制性能。
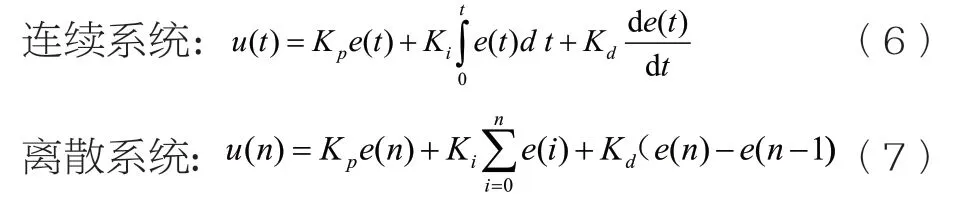
2.2 适应度函数的确定`
文章主要是对水轮机调节器的参数进行二次优化。首先根据给定值对模块进行优化,得到优化后模块的Kp值,然后将其固定,按照扰动抑制模块进行优化,得到KiKd值。最终得到一组最优KpKiKd值,使系统的调节稳定时间更短,超调量更小。同时,采用ITAE准则作为性能指标函数,它的定义为:

式中:t为时间;e(t)为误差。
3 仿真分析与结果分析
通过对水轮机调速器的数学模型进行Matlab/Simulink平台下仿真实验,验证CSA算法的有效性与可靠性,并且与PSO算法就行对比。对于数值固定的模型参数如表1。

表1 水轮机传递系数
CSA算法的参数设置为:最大迭代次数为200,种群总数为30。优化参数的设置为:Kp、Ki、Kd的上限为10,下限为0。
3.1 空载工况实验仿真
将模型置于空载情况下,对仿真机施加5%的频率扰动。实验结果如图3~图4所示。

图3 5%频率扰动转速响应曲线
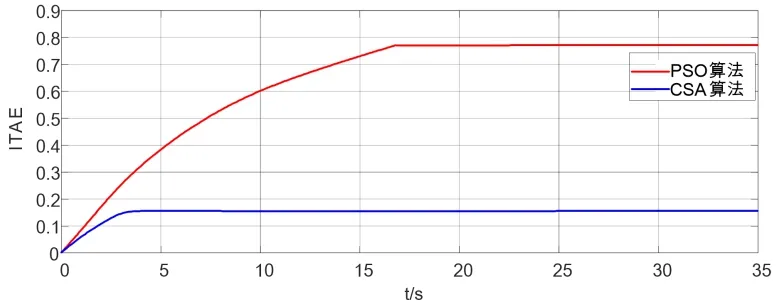
图4 ITAE指标响应曲线
从图3可知,在空载工况5%频率扰动中,采用PSO算法的PID调节系统,其超调量较大,调节时间较长,PID最优参数值为Kp=3.01,Ki=1.37,Kd=2.49;采用CSA算法的PID调节系统,其超调量小,调节时间短,调节效率高,PID最优参数值为Kp=3.86,Ki=1.05,Kd=2.94。从图4可知,CSA算法的转速偏差ITAE指标更小,更早趋于稳定,表明CSA算法性能要远高于PSO算法。
3.2 负荷工况实验仿真
当水电站的负荷端扰动会造成供电频率的波动,系统需要做出响应稳定供电频率。为了验证CSA算法的调节能力,设置孤网10%的负荷扰动实验。实验结果如图5~图6所示。

图5 10%负荷扰动转速响应曲线

图6 ITAE指标响应曲线
从图5可知,在孤网10%的负荷扰动实验中,采用PSO算法的PID调节系统,其超调量大,调节时间较长,稳定时间长,系统波动较大,PID最优参数值为Kp=4.26,Ki=1.58,Kd=2.84;采用CSA算法的PID调节系统,其超调量小,调节时间短,系统达到稳定时间短,PID最优参数值为Kp=5.13,Ki=1.16;Kd=3.22。图6可 知,CSA算 法的ITAE指标更小,系统收敛时间短,CSA算法性能更优。
4 结论
为提高水轮机PID调速器的参数质量,文章提出了一种基于乌鸦算法的水轮机调速器参数优化。相较于用传统方法优化,使用CSA算法收敛速度更快,有效避免局部最优,有更好的鲁棒性。在空载工况实验和负荷工况实验仿真中,验证了CSA算法在优化调速器参数,其超调量小,调节时间短,系统稳定快,调节效率高,ITAE指标更小。
