每章一练之“轴对称图形”

文／王 平

说明：本组练习题分为两个版块，第一版块是达标训练，第二版块是提升训练。在达标训练中，每一道题都进行了分类——A类题是基础型练习，B类题是发展型练习。同学们可根据自己的需要选择其中一类完成。

一、达标训练

1.（A类）如图1，线段AB和A′B′关于直线l对称，连接AA′，则l与AA′的关系是____________。

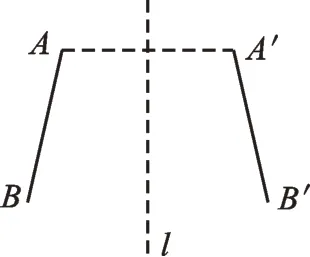
图1

（B类）根据示例图形，完成下表。

图形的变化平移示例图形与对应线段有关的结论AB=A′B′AB∥A′B′与对应点有关的结论AA′=BB′AA′∥BB′轴对称

2.（A类）如图2，在△ABC中，BC=10，∠BAC=110°，AB、AC的垂直平分线分别交BC于点D、E，连接AD、AE，则△ADE的周长为______，∠DAE的度数为_______°。

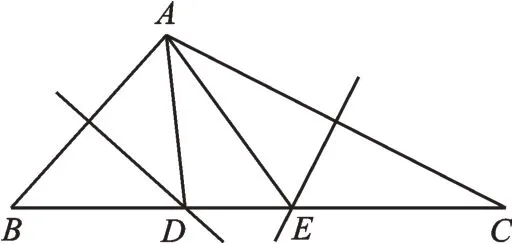
图2

（B类）如 图3，在△ABC中，BC=a，∠BAC=α°（α＜90），AB、AC的垂直平分线分别交BC于点D、E，DE=b，连接AD、AE，则△ADE的周长为_______（用含a、b的代数式表示），∠DAE的度数为_______°（用含α的代数式表示）。

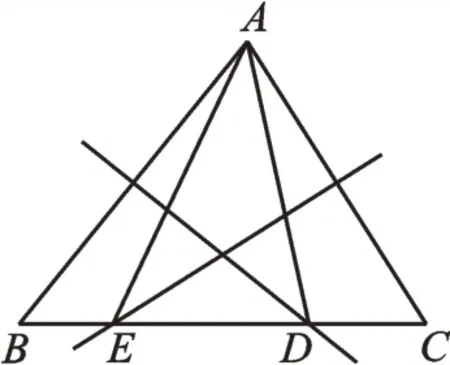
图3

3.（A类）如图4，在△ABC中，AD是BC边上的高，且AD平分∠BAC。求证：AB=AC。

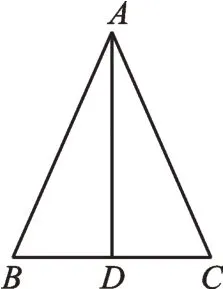
图4

（B类）如图4，在△ABC中，AD是BC边上的中线，且AD平分∠BAC。求证：AB=AC。

4.（A类）如图5，△ABC和△CDE均为等边三角形，且点A、C、E在一条直线上，连接AD、BE。求证：AD=BE。

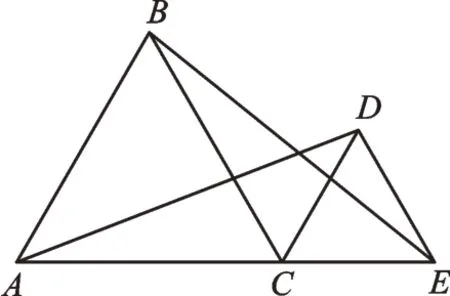
图5

（B类）如图6，△ABC和△CDE均为等边三角形，连接AD、BE交于点O。求∠AOB的度数。

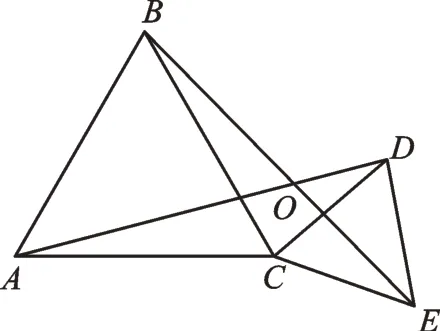
图6

二、提升训练

1.如图7，已知线段a、h，求作一个等腰三角形ABC，使△ABC的腰长为a，腰上的高为h。

图7

2.用两种方法证明“直角三角形斜边上的中线等于斜边的一半”。（画出图形，写出已知、求证和证明。）