考虑天然气水合物上覆层不排水抗剪强度深度变化的海底斜坡稳定性影响分析
2022-11-01修宗祥孙永福刘绍文宋玉鹏董立峰宋丙辉
王 辉 ,修宗祥,孙永福, ,刘绍文,宋玉鹏,董立峰,宋丙辉
1. 南京大学 地理与海洋科学学院,南京 210023;2. 自然资源部 第一海洋研究所,青岛 266061;3. 青岛海洋科学与技术国家实验室 海洋地质过程与环境功能实验室,青岛 266061
1 引言
天然气水合物(以下简称水合物)因其储量大、分布广、能量高、污染小等特点,逐渐占据全球主要大国能源竞争的核心地位。我国拥有丰富的海洋水合物资源,仅在南海北部陆坡远景区其资源量就达数百亿吨油当量,水合物资源潜力巨大(刘杰等,2016)。随着中国油气资源勘探开发事业的发展,越来越多的水合物试开采工程逐渐向深水区推进。由于水合物的赋存状态影响海底斜坡地层的力学强度,含水合物地层的不稳定性构成了深水工程灾害的潜在条件(柏泽等,2017),与水合物有关的深水工程安全问题已日益受到关注。天然气水合物分解对海底滑坡稳定性的影响是当前海洋实际工程中亟待查明的问题,对于地质灾害防治和指导深水安全作业具有重大的应用与学术价值。
含水合物海底斜坡的稳定性受上覆海水深度、坡角、水合物储层覆盖层深度、水合物沉积层厚度、水合物饱和度、水合物分解程度等因素影响(Sultan et al., 2004;Xu and Germanovich,2006;刘锋等,2010;鲁力等,2014;宋本建等,2018; Song et al.,2019;Wei et al.,2019)。水合物分解降低了海底斜坡的稳定性,甚至导致海底滑坡的观点已被广泛接受。一方面,水合物的存在会增强周围地质环境的地层强度,当其分解后,会降低周围沉积物储层的地质力学稳定性,诱发海底滑坡等地质灾害,威胁海洋工程安全(Grozic et al.,2001;彭晓彤等,2002);另一方面,海洋浅层土体长期受海水冲刷和浸泡作用,斜坡土体结构松散,强度较低,受地质构造作用与人为勘探施工扰动,易发生失稳。这将导致下方水合物储层的赋存环境改变,引发水合物的分解。而水合物的分解反过来也会弱化较深部地层的强度,引起更大规模的斜坡失稳,带来巨大的负面环境效应和灾害影响。
深海沉积物在自重作用下固结,不排水抗剪强度随其上覆压力增加而增加(修宗祥等,2016)。前人分析含水合物储层的海底斜坡稳定性时,通常认为水合物储层的上覆层土体为均质,其强度指标参数为定值(曹杰峰等,2013;张振飞等,2016;宋本健等,2018;李天赐等,2019)。这样只考虑了水合物分解引起的沉积层强度弱化作用,忽略了水合物储层上覆土体强度分布的非均质性。土体的非均质性会显著影响土体的抗剪强度,进而影响稳定性计算结果。因此,进行含水合物储层的海底斜坡稳定性分析时,需要综合考虑上覆土体不排水强度的非均质性和水合物分解引起的储层强度弱化的共同作用,以往的研究大多只考虑了其中一个因素的影响,将两者结合分析的研究较为少见。
本文基于南海神狐海域地形地貌数据以及部分地质钻孔测试数据,结合研究区水合物赋存特征,考虑海底浅层土强度的垂向非均质性的影响,利用有限元软件ABAQUS,采用强度折减法进行该区海底斜坡的稳定性分析,对不同影响因素作用下潜在海底滑坡进行了模拟,讨论海底滑坡发生的可能性,在此基础上讨论水合物分解对海底斜坡的稳定性以及失稳规模的影响。研究成果能为南海神狐海域的水合物试采区选址、安全开采及灾害预防等提供科学依据,以便在工程实践中采取积极、主动的应对措施,降低工程风险。
2 区域地质背景
研究区南海北部神狐海域位于南海北部大陆坡的中段(图1),构造上属于珠江口盆地珠二坳陷的白云凹陷,地处大陆架到深海的大陆坡过渡带。珠江口盆地为一新生代沉积盆地,沉积层演化经历三个阶段:晚白垩世—早渐新世陆相沉积、晚渐新世—早中新世海相沉积,中中新世—现今,沉积地层由下到上依次为粤海组、万山组和琼海组(曾小明,2014),最终形成了以海相沉积为主导的区域性沉积层(李平鲁等,1995;Ma et al.,2015)。该区水深约1000~1500 m,地形起伏较大,中部地区发育峡谷地貌,呈现“南低北高、西低东高”的特征。白云凹陷具有洋—陆过渡型地壳,区域地温场偏高,中新世以来新构造运动逐渐增强,沉积速率高,产生了大规模的流体底辟构造,在不同深度形成了高角度断裂和垂向裂隙,这为神狐海域水合物成藏富集提供了通道条件(吴能友等,2009;龚跃华等,2009;张伟等,2017)。

图1 南海北部珠江口盆地构造及其研究区位置(改自周庆杰,2015)Fig. 1 Sketch showing the tectonic subdivision of the Pear River Mouth Basin and the studying area
广州海洋地质调查局先后于2007、2015及2016年在该区域进行了天然气水合物钻探航次,均成功钻获了天然气水合物实物样品(Yang,2017),并于2017年和2020年成功实施了海域水合物试采工程(叶建良等,2020),证实了该区具有较大的天然气水合物资源潜力。研究区水合物分别以厚层状、分散状、薄层状、斑状和在断层附近(杨胜雄等,2017)分布在海水深度超过1000 m水深的海底,赋存于未固结成岩的黏土质粉砂和粉砂质黏土等沉积物中(周守为,2014;Li,2018;叶建良,2020),平均坡度为 3.3°~3.6°,局部坡度大于 13°,最大坡度达25°。储层埋深变化较大,大约在海底以下50~300 m的范围内,有效厚度估计为10~80 m(张伟等,2017;吴时国,2018)。水合物沉积物的孔隙度为33%~48%,平均饱和度约为13.7%~50%。从现有试采情况和技术水平来看,我国海域水合物实现商业开发所需具备的储层特征可能包括:平均水合物饱和度应超过30%,储层厚度应大于40 m(于兴河,2014;Yang,2017;宁伏龙等,2020)。
该区发育海底滑坡/滑塌、地震、活动断层、侵蚀沟谷、岩浆底辟、泥底辟等灾害地质因素(王宏斌等,2003),成为天然气水合物稳定赋存安全开采中不可忽视的影响因素。该区因丰富的天然气水合物资源储量与较高的研究程度也是进行含水合物储层海底斜坡稳定性分析的理想研究靶区。该区有水合物分布的海底斜坡进行多因素影响下的稳定性评价对水合物勘探开发的安全运行具有重大意义。
3 方法与模型构建
3.1 稳定性分析方法
有限元强度折减法是通过引入一个折减系数(Fs),令外荷载保持不变的情况下,人为地对斜坡土体的强度参数进行同比例折减直至斜坡破坏,使斜坡达到极限状态来分析斜坡变形及其稳定性问题的方法,此时的折减系数即为斜坡的安全系数,属于数值分析法的范畴(赵尚毅等,2002;郑颖人等,2002;罗荣等,2012)。因为其不受斜坡几何形状、边界条件、材料的不均匀性以及各种外部荷载作用的限制,可以真实地模拟斜坡的破坏过程,并提供应力、应变和位移等全部信息(杨林青,2012)。该方法一经提出就被国内外学者广泛应用于斜坡稳定性分析中。
以斜坡稳定性中最常用的破坏准则——摩尔—库伦准则为例,可按照下式来表示强度折减安全系数:

其中,c和φ是土体的抗剪参数,分别为实际黏聚力与内摩擦角;cm和φm为折减后土体的黏聚力与内摩擦角;Fs为强度折减系数,斜坡达到极限破坏状态时的Fs即视为安全系数。
研究区水合物的赋存区域的上覆层土体主要为粘性土,渗透系数较小(李彦龙等,2019),且滑坡过程较为快速发生,因此可以近似为不排水过程。实际的海底斜坡由于受各种自然因素影响,其土层的分布多样的,不排水抗剪强度也往往呈现出分段的特征。研究区的工程地质勘探数据也表明在钻孔处土层的不排水抗剪强度呈现出分段线性增长的特征。因此,该区海底稳定性分析时应考虑不排水抗剪强度的变化。一定深度内土层的不排水抗剪强度可认为随着深度的增加而近似线性增加(Wang et al.,2010;修宗祥,2016):

其中,su为表层土的不排水抗剪强度;k代表强度增长斜率(kpa·m-1);z代表土层埋深厚度。考虑到实际海底斜坡土层的分布情况,式(2)可表示为:

其中,sun为第n层土的表层不排水抗剪强度;kn代表第n层土的强度增长斜率(kpa·m-1);zn代表第n土层埋深厚度。此时,不同埋深土体的折减后强度smn可以表示为:

由上所述,在进行海底斜坡稳定性分析过程中,因充分考虑斜坡土体分层导致的强度分布不均的情况,通过对不同土层的不排水抗剪强度进行强度折减来进行斜坡稳定性分析,可使得分析结果增加精确。
有限元强度折减法基于大型通用有限元软件ABAQUS来完成,有限元模型的构建包括以下步骤:几何图形生成、本构模型参数设定、施加力和边界条件及网格剖分。根据海底地形数据及浅地层剖面影像,确定模型尺寸及和海床土层分布,建立滑坡几何模型;参数取值参考研究区已有的钻孔数据与海底土体物理力学研究资料、水合物储层强度指标实验结果以及已有的相关数值模拟进行选取。
需要考虑不排水强度随深度的变化,因此这里按照分段线性设计,土层强度随深度的变化通过设置场变量来实现;根据不同的模拟方案,施加作用在斜坡上的荷载和边界条件;采用平面四边形应变单元(Abaqus中的CPE4单元)剖分土体。最后为了保证计算模型的准确性,在ABAQUS/CAE中做如下检查:原位和室内试验得到的强度参数是否正确赋予各土层;边界条件是否准确施加;是否有畸形单元。检查无误后,即可进行不同方案下的斜坡稳定性计算。
3.2 数值模型及参数选取
本文模型草图参照广州海洋地质调查局2015年GMGS3航次钻探W19站位据地震资料解释结果(图2)及钻井数据,模拟中国南海神狐海域水合物富集区海底斜坡在多种影响因素作用下的稳定性。模型的基本尺寸如图3所示,模型水平跨度为2000 m,斜坡角度为5°,水合物埋深135 m,水合物沉积层厚度为35 m,斜坡水平跨度1100 m,坡顶水深1200 m。海床自上而下分别为上覆层、含水合物沉积层以及下卧层。本模型为基本模型,后续模型在本模型基础上依据不同评价方案进行适当修改。

图2 过神狐海域的W19和W18井地震剖面(靳佳澎等, 2017)Fig. 2 The seismic profile crossing the W18 and W19 boreholes in the ShenHu offshore area

图3 研究区斜坡稳定性分析的斜坡几何模型Fig. 3 Slope geometry model for the stability analysis in this study
结合已有的区域地质资料、海底钻孔取样及实验结果等资料获取地层的物理力学参数。水合物上覆层纵向上土类分布较为一致,由上至下其压实程度逐渐增大(杨敬红等,2014)。邻井全井段取心结果显示,该区块水合物上覆地层为典型的钙质黏土层(李彦龙等,2019)。根据南海北部神狐海域W18/19站位水合物上覆层的CPTU测试结果和室内实验数据的推算结果(胡高伟等,2017;李彦龙等,2019),将地层划分为三个层段,具体的不排水抗剪强度分布如表1所示。水合物储层的强度指标参考骆汀汀等(2020)基于原位水合物沉积物重塑样品的实验结果建立的力学经验公式,水合物未分解时,其黏聚力和内摩擦角分别取0.89 MPa和22.5°(水合物饱和度取W19井水合物储层的平均饱和度,Sh=46.2%);水合物分解过程中,其黏聚力随着饱和度减小而线性降低(图4),内摩擦角保持不变。具体参数分布如表2所示。模型边界条件的设置参考了典型边坡失稳分析案例,对左右边界进行了水平方向上的位移限制,对于下部边界则进行了各方位的位移限制。

表1 南海神狐海域不含水合物沉积层的土体力学参数Table 1 Physical and mechanical properties of strata without gas hydrate in the Shenhu offshore area of the South China Sea

表2 饱和度(Sh)为46.2%时水合物沉积层的土体力学参数Table 2 Physical and mechanical properties of strata with gas hydrate(Sh=46.2%)

图4 南海神狐海域水合物储层强度参数与水合物饱和度的关系Fig. 4 The relationship between the hydrate bearing formation strength and hydrate saturation in the Shenhu offshore area of the South China Sea
4 稳定性结果分析
4.1 考虑水合物分解下斜坡几何特征的影响
根据研究区的地形特征,在基础模型(图3)参数设计的基础上,分别以 3°、5°、7°、10°、13°五种模型来模拟坡角对斜坡稳定性的影响;此外,改变基础模型中斜坡段的水平长度,讨论斜坡段水平长度变化对斜坡安全系数的影响。
图5、6显示了不同水合物分解程度下,斜坡坡度变化对斜坡安全系数的影响效果。由图5可知,设计斜坡工况下,无论水合物是否分解,安全系数都随斜坡坡度的增大而逐渐降低,这是由于土层强度一定时,安全系数主要取决于斜坡的坡度。需要说明的是,当坡度为10°和13°时,斜坡的安全系数小于1,表明此时斜坡已失稳,这主要是由于计算采用的土层强度参数低于海底真地形坡度下的强度值。因此,如何获取更准确的土层力学参数,是海底斜坡稳定性分析的关键。图5、6同时可以看出,水合物分解前后的安全系数基本不变,最危险滑动面位于上覆层浅部。表明模型设计水合物埋深和分解范围条件下,分解后过水合物层滑动面的安全系数仍高于上覆层浅部的滑动面安全系数。因此,水合物上方浅部地层的稳定性应给予更大关注,特别是浅部地层强度相对较低、地形坡度相对较大的区域,避免因自然条件或工程扰动造成浅层滑坡,从而破坏工程设施。

图5 坡度对斜坡安全系数的影响Fig. 5 Effect of the slope angle on the safety factor of the slope
图7为5°斜坡角度下,不同斜坡段水平长度对应的斜坡安全系数和潜在滑动深度。可以看出,水合物未分解状态下的斜坡安全系数与滑动深度并未发生较大改变,最危险滑动面均位于上覆层浅部。水合物分解后,当斜坡段长度为1100 m时,最危险滑动面仍位于上覆层浅部,但随着斜坡段水平长度的增加,水合物分解后抗滑力减小的程度越来越大,最危险滑动面变为过水合物层的顶界,斜坡的安全系数越来越低。这表明水合物分解范围、埋深、地形坡度以及上覆层土层力学参数的组合,决定了最危险滑动面的出现位置和安全系数的大小。下文中将则对特定坡度下,上述因素变化对斜坡稳定性的影响进行讨论分析。
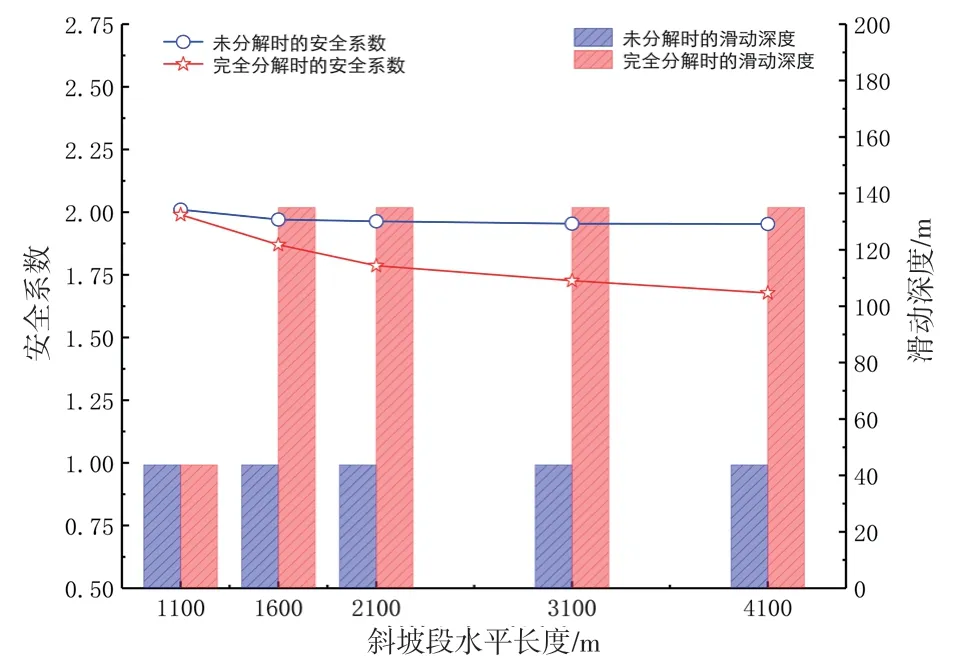
图7 斜坡段水平长度对斜坡稳定性的影响Fig. 7 Effect of horizontal length of the slope section on the slope stability
4.2 土体不排水抗剪强度对含水合物储层的海底斜坡稳定性的影响
针对土体不排水抗剪强度对稳定性分析的影响,通过引入变量 a 改变上覆层不排水抗剪强度的分布,即式(3)变为
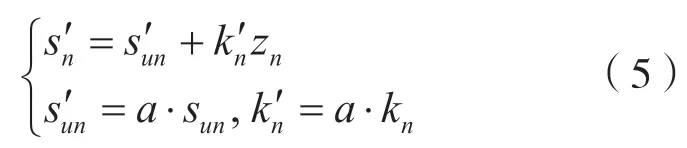
通过对a赋值,在图3所示的模型的基础上设计了7种方案分析考虑水合物分解情况下不同不排水抗剪强度对斜坡稳定性的影响。具体方案设置如表3所示。

表3 模拟方案设置及具体描述Table 3 Design and description of numerical simulation scheme

图6 部分坡度下水合物分解前后计算终止时的位移云图Fig. 6 Contours of displacement under different slope angles with/without hydrate decomposition
研究表明,水合物未发生分解时,斜坡的安全系数与上覆层不排水抗剪强度成正相关关系(图8),这符合安全系数的定义,也即斜坡的抗破坏能力随着土体不排水抗剪强度的增大而加强。当水合物开始分解时,上覆层土体强度较低的斜坡的安全系数基本保持不变,且低于经过水合物层滑动面的安全系数,最危险的滑动面仍位于上覆层浅部(图9 a, b)。当上覆层土体强度相对较大时,由于浅部滑动面的安全系数相对较高,最危险滑动面位置取决于水合物的分解范围。随着水合物分解程度的扩大,经过水合物层滑动面的安全系数逐渐降低,当水合物分解程度达到75% 时,此时经过水合物层滑动面的安全系数要低于上覆层浅层滑动面的安全系数,成为最危险滑动面。图9c、d展示了水合物分解前后最危险滑动面。图10为不同方案下水合物分解前与完全分解后斜坡最危险滑动面的滑动深度与安全系数。可以看出,不同方案对应的最危险滑动面位置与安全系数也对应了上述规律。如方案1到方案五,由于其上覆土层强度较低,最危险滑动面始终位于上覆层浅部;而方案6和方案7时,由于水合物完全分解时产生较大程度的强度降低,最危险滑动面的滑动深度也随之增加至水合物层的顶界。

图8 不同方案下的安全系数Fig. 8 Curves of the safety factor with different designed schemes
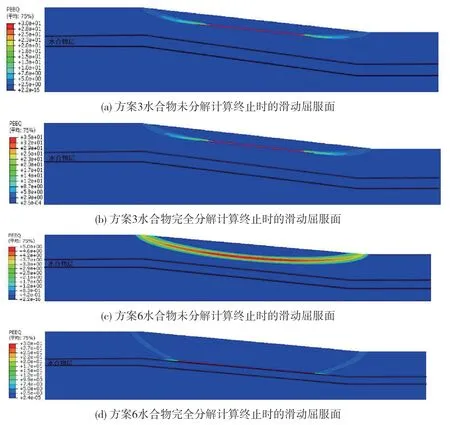
图9 部分方案下计算终止时的滑动屈服面Fig. 9 The yield surface of several cases after calculation ending

图10 不同方案的安全系数与计算终止时的滑动深度Fig. 10 Safety factor and sliding depth of different schemes
4.3 水合物上覆层厚度的影响
考虑研究区水合物层的埋深范围,讨论分析不同埋深对斜坡稳定性的影响。因此,在方案3与方案6的基础上,只改变水合物沉积层的上覆层厚度,其中最浅埋深为50 m,最深埋深为250 m。水合物未分解与水合物完全分解对应的斜坡稳定性分析结果如下:
图11a反映了方案3下不同水合物埋藏深度对斜坡稳定性的影响。当水合物未发生分解时,随着埋藏深度的增加,斜坡安全系数的变化并不显著,此时,水合物层的存在对斜坡的影响甚微,其稳定性取决于斜坡自身的强度,最危险滑动面位置出现在水合物层上覆土体浅部。考虑水合物分解时,水合物层对斜坡的稳定性影响,存在一临界埋深值。方案3工况下,当埋藏深度小于135 m,水合物分解降低了斜坡的稳定性,安全系数下降,失稳规模因水合物分解而增大,最危险滑动面位于水合物层的顶界。而当水合物埋深大于135 m时,水合物分解对斜坡的稳定性系数几乎没有影响,且最危险滑动面的位置始终位于上覆层浅部。
图11b为方案6强度分布下不同水合物埋藏深度对斜坡稳定性的影响。可以看出,当水合物层埋深低于不含水合物斜坡的最危险滑动面深度时,未分解状态下的水合物沉积层相当于一个坚硬的夹层,可限制斜坡失稳的规模,此时对应的滑动面深度始终小于水合物的埋深。这也与图11c、d所示的(对应方案6强度分布)不含水合物层与含水合物(未分解)的最危险滑动面特征相符合。当水合物完全分解时,水合物埋深较浅(小于临界埋深时)的安全系数,比未分解状态下的安全系数低,最危险滑动面的深度由上覆层浅部下移至水合物层顶界。当水合物埋深逐渐增大至200 m时,此时已超过方案6工况对应的临界埋深,最危险的滑动面位于上覆层浅部,水合物的分解不再对其产生明显影响。
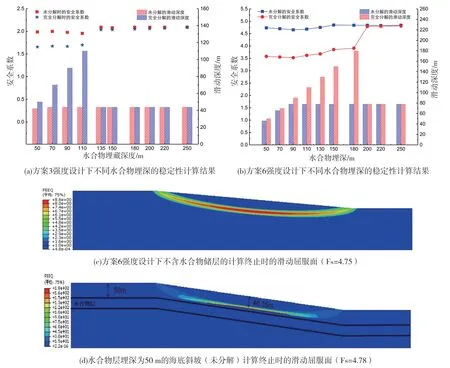
图11 水合物埋藏深度的对斜坡稳定性的影响分析Fig. 11 Effect of the burial depth of hydrate-bearing layer on the slope stability
4.4 水合物沉积层厚度的影响
为探明水合物沉积层厚度对含水合物储层的斜坡稳定性的影响,以基础模型设置为参考,结合水合物研究背景,假设储层的水合物饱和度一定,水合物储层的厚度以10~80 m为范围,在方案3的几何模型和上覆层(水合物层埋深135 m)强度分布的基础上,以20 m为增量设计了如下的计算模型和相应的计算结果(表4)。

表4 不同水合物储层厚度计算模型设计Table 4 Calculation models with different hydrate reservoir thickness
由图12可以发现,随着水合物储层厚度的变化,斜坡整体稳定性在水合物分解前后并没有发生明显改变。因此,当水合物储层处于或者大于临界埋深时,即使水合物分解层厚度增加,其对斜坡整体的稳定性影响也较小。
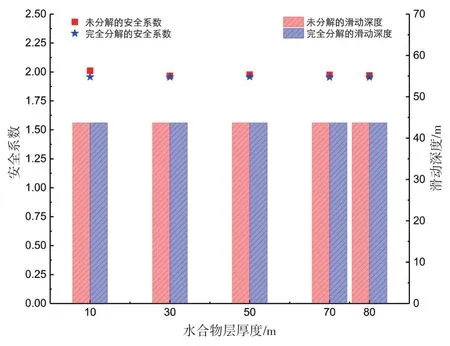
图12 水合物沉积层厚度对斜坡稳定性的影响Fig. 12 Effect of the hydrate-bearing layer thickness on the slope stability
5 结论
本文基于强度折减法,依据钻孔数据按深度设计了水合物层上覆土体的不排水抗剪强度分布,系统分析了包括斜坡几何参数、土体强度分布以及水合物储层特征、水合物分解等因素对海底斜坡稳定性的影响规律,得出以下结论:
当不考虑水合物的分解时,斜坡的坡度和地层强度对含水合物储层的海底斜坡稳定性起主要控制作用。海底斜坡的安全系数与坡度成负相关,与土体强度成正相关,斜坡的水平长度和水合物储层的埋深、厚度对斜坡的安全系数的影响不大。此时,斜坡最危险滑动面皆位于浅部,主要表现为浅层滑坡。
当考虑水合物的分解时,斜坡整体的稳定性受到水合物分解导致的土层强度降低的影响,影响程度取决于水合物储层的位置。对于指定的海底斜坡,受地形几何特征、上覆层土层强度分布等因素的控制,水合物层的埋藏深度存在一特定的临界值(临界埋深)。当水合物层埋深处于临界埋深以浅时,水合物的分解降低了斜坡稳定性且扩大了斜坡的失稳范围,在水合物完全分解时,最危险滑动面位置经过水合物层,此时表现为深层滑坡。当水合物的埋藏深度超过临界埋深时,水合物的分解对斜坡的稳定性影响较小,最危险滑动面位置位于上覆层浅层,表现为浅层滑坡。
根据目前模型中的水合物埋深情况,水合物分解后深层滑动面的安全系数仍高于浅部地层,表明相对于水合物分解对斜坡稳定性的影响,研究区由于浅部地层自身强度较低且局部坡度相对较大,该区域的海底滑坡灾害主要为浅层滑坡。因此,对于该海域的天然气水合物开采来说,其浅部地层的海底滑坡灾害风险仍然需要关注。
