基于蒙特卡洛法的大风区接触网系统可靠性分析
2022-11-01陈子文王彦哲
陈子文,王彦哲,陈 可
0 引言
牵引供电系统是保障电气化铁路安全运营的重要系统之一,其安全可靠性直接关乎着列车运行的安全。研究表明,供电系统的可靠性95%以上取决于接触网的可靠性[1],因此对接触网可靠性的研究是重中之重。随着近年来我国铁路开通里程的不断增加,接触网的可靠性成为了热门的研究课题。目前,解析法和模拟法被普遍应用于接触网的可靠性研究中。解析法是根据系统元件的结构与功能,以及元件之间的逻辑关系建立相应的可靠性模型,从而计算出接触网系统的可靠性。解析法因其原理简单,计算方便,目前已经成为接触网可靠性研究的主要方法。文献[2]采用故障树法通过建立接触网系统可靠性模型对接触网可靠性进行了定量和定性分析,但其需要进行不交化,计算过程较为繁琐。文献[3]采用GO 法实现了牵引供电系统可靠性的评估,该方法虽然原理简单,但仍需要求最小割集,随着系统的复杂度增加,计算过程也较为繁琐。文献[4]采用马尔科夫法分析了接触网系统的可靠性,但其仅仅是在设备相互独立的情况下进行的分析,与实际情况存在误差。随着铁路的不断发展,对接触网的可靠性要求越来越高,对影响其可靠性因素的研究也日趋精细。
兰新高铁位于我国西北地区,运行环境位于西北大风区。接触网作为重要系统常年暴露在风沙条件下,对列车的运行安全造成了很大的影响[5]。本文针对风因素对接触网的可靠性影响进行分析。因融合了风因素后接触网系统的复杂度增加,解析法在研究过程中计算量呈指数级增加,因此其已经不再是接触网可靠性分析的首选方法。蒙特卡洛法因其不受系统规模的影响,比解析法更能反映接触网系统的实际情况,特别适用于复杂系统可靠性的研究。因此,本文拟采用蒙特卡洛法融合西北大风区的特点对大风区接触网系统进行可靠性研究。
1 蒙特卡洛法基本原理
1.1 方法简介
蒙特卡洛模拟是一种通过设定随机过程不断重复生成随机数列,并计算估计参数估计量和统计量的方法。目前,蒙特卡洛理论在很多方面得到了应用,如数学、工程以及经济等领域[6],主要用于解决无法采用确定性模型解决的实际问题。蒙特卡洛法的应用基础是数理统计理论,在累计处理多次抽样输入后得到系统的可靠性指标,其最大优点是模拟次数与系统规模无关,适合于复杂系统和实际运营系统,其可靠性精确度主要取决于抽样次数,因此为了提高计算精度并符合要求,必须增加抽样的次数。
1.2 元件的基本抽样
利用蒙特卡洛方法进行接触网系统的可靠性分析时,首先要对接触网系统内各元件的状态进行抽样,系统元件主要包括各种组成部件。

在一个系统中,其元件i的故障率为λi,Xi为其一个运行状态。假设R是随机分布在(0,1)区间的一个随机数,则有对于一个包含m个元件的系统,其元件的状态矢量为X= (X1,X2, …,Xm),对应的x= (x1,x2, …,xm)为其对应矢量的数值。根据各元件的故障率和逻辑关系可以求出其联合分布函数。当各元件独立时有


2 基于Weibull 分布的风速模型
2.1 风速Weibull 模型的建立
我国西北地区尤其是甘肃、新疆地区风能资源最为丰富,风能可用于发电,但其对列车的运行安全是一种威胁。近些年因为大风导致的受电弓脱弓现象时有发生。研究风对接触网可靠性影响的首要任务是对沿线的风速进行模拟。
风速是设计中必需考虑的重要参数。对风的预测方法主要分为两类:一类是寻求风与其他气象要素之间的线性和非线性关系,另一类是通过分析风的时间序列或风的概率分布函数来建立模型预测。上述两种方法均是基于概率和数理统计的预测方法[7]。用于拟合风速概率分布的模型有很多,常用的有韦布尔(Weibull)分布、瑞利(Rayleigh)分布等,其中应用最为广泛的是两参数Weibull 分布。Weibull 分布是Weibull W 在1939 年提出的一种连续型分布[8],因其变换形式灵活、函数形式简单,且能很好地模拟自然现象,因而受到广泛关注。两参数Weibull 分布的概率分布密度函数为

式中:ui为符合0~1 均匀分布的随机数,将C、K参数代入后即可以求得风速的模拟值。
2.2 C、K 参数的计算


文献[10]根据甘肃酒泉区域6 个测风塔不同高度层(10、30、40、50、70 m)的测量资料,利用式(10)、式(11)计算出了该区域的韦布尔分布参数。考虑到接触网分布在距离轨道10 m 左右的高度,本文对相关数据进行筛选,选取了10 m 高处的参数计算结果,相关韦布尔参数见表1。
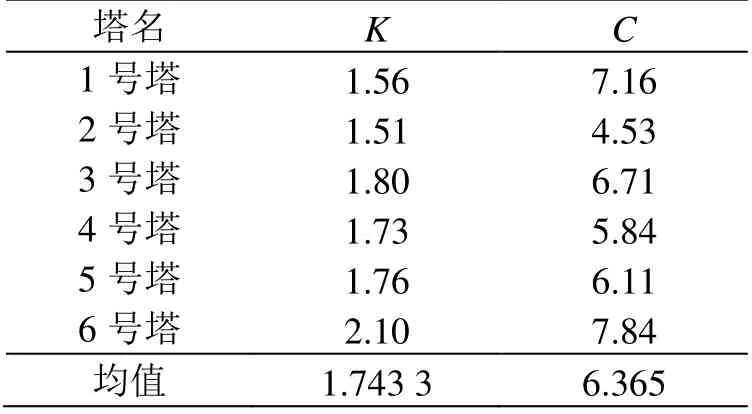
表1 10 m 高处韦布尔参数计算
对计算结果求均值可得K= 1.743,C= 6.365。
3 基于蒙特卡洛法的接触网系统可靠性分析步骤
3.1 接触网可靠性模型的建立
接触网系统由接触悬挂、定位装置、支柱与基础、支持装置组成。根据FTA 法(故障树分析法),画出接触网失效的故障树。本文采用文献[11]所述的接触网模型进行可靠性分析,接触网故障树模型如图1 所示。
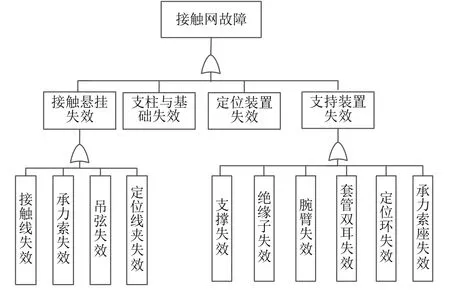
图1 接触网故障树模型
由图1 可知,接触网系统为串联系统,任何一个部位的故障都会引起整个系统的瘫痪。本次计算中将指标选取为接触网可靠性,取值范围为(0,1)。
表2 中接触网基本事件发生概率是根据调研收集到某段铁路常年的故障统计结果,分析接触网各部件的年故障率得到的。
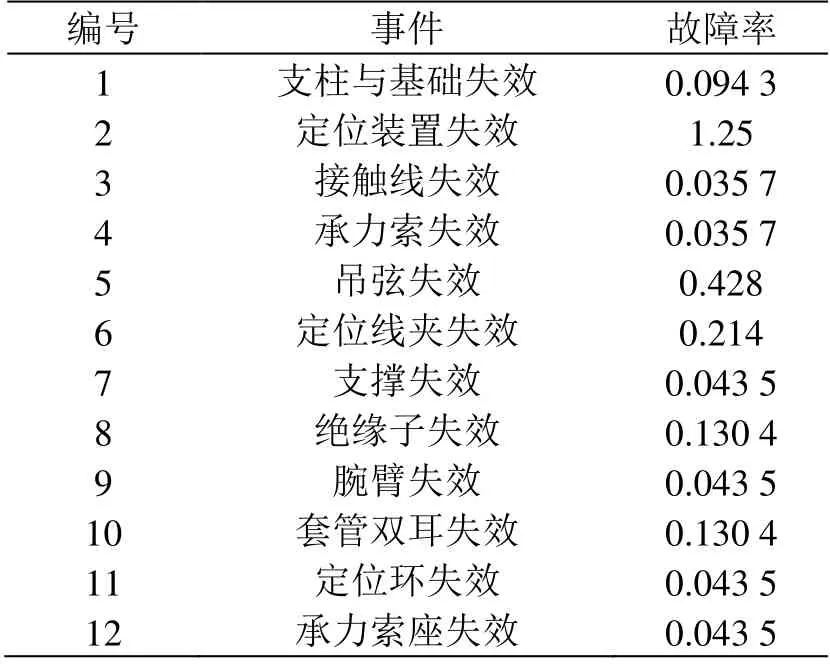
表2 接触网系统各部件年故障率
3.2 风速影响系数的选取
研究表明:当风速小于5 m/s 时,脉动风对接触压力影响不大;当风速大于10 m/s 时,接触压力峰值迅速升高,接触力标准偏差、离线率迅速增大,受流情况严重恶化;当风速达到20 m/s 时,接触压力峰值达到536.01 N,离线率达到15.79%,将会产生较为严重的拉弧现象。因此在实际运行中,需限速或采取适当的防风措施[12]。
基于此,本文将风速划分为4 个等级,每个等级对应不同的影响系数s。当风速低于5 m/s 时影响系数为1(可以认为无影响),风速为5~10 m/s时影响系数为1.05,风速为10~20 m/s 时影响系数为1.1,风速大于20 m/s 时影响系数为1.157 9。
3.3 蒙特卡洛法的Matlab 实现步骤
在确定相应元件指标后,对接触网系统的可靠性蒙特卡洛算法进行Matlab 编程计算,计算步骤如图2 所示。
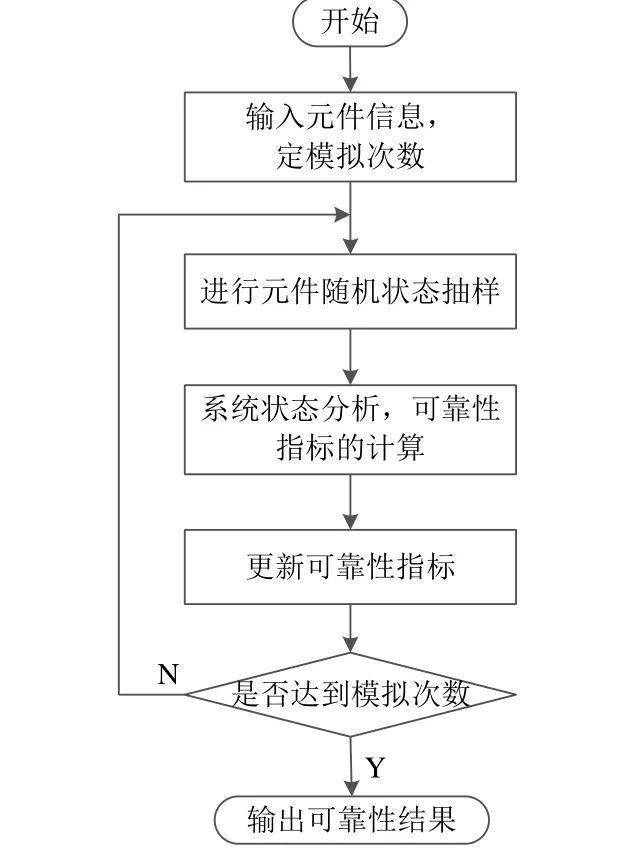
图2 基于蒙特卡洛方法可靠性分析流程
仿真时,随机数生成采用rand 函数,仿真次数分别为1 000、10 000、100 000 次,在仿真中可以采用方差系数或抽样次数作为终止抽样的判断依据,本文采用抽样次数N作为计算终止的判据。
将第2 节计算所得的Weibull 参数变量K=1.743、C= 6.365 代入式(9)求得风速。在Matlab程序中分别模拟抽样1 000、10 000、100 000 次求得对应的风速分布如图3 所示。
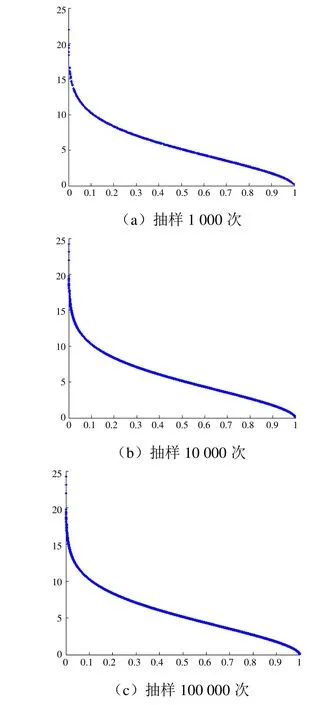
图3 抽样风速分布
由图3 可知,在模拟进行10 000~100 000 次后风速分布稳定在0~25 m/s,风速分布趋向于稳定,表明采样样本已经足够大。利用Matlab 对接触网可靠性曲线进行模拟可以得到如图4 所示接触网可靠性随时间变化的曲线。
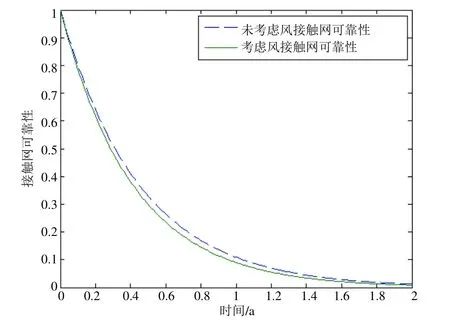
图4 接触网可靠性随时间变化曲线
由仿真结果可以看出,随着接触网的运行,初期接触网可靠性下滑比较严重,随后在融合了风因素之后接触网可靠性明显下降。为了更加直观分析,在变化曲线上分别选取0.3 a、0.6 a、1 a 3 个时间点所对应的可靠度数据,对其可靠性进行对比分析,分析结果见表3。
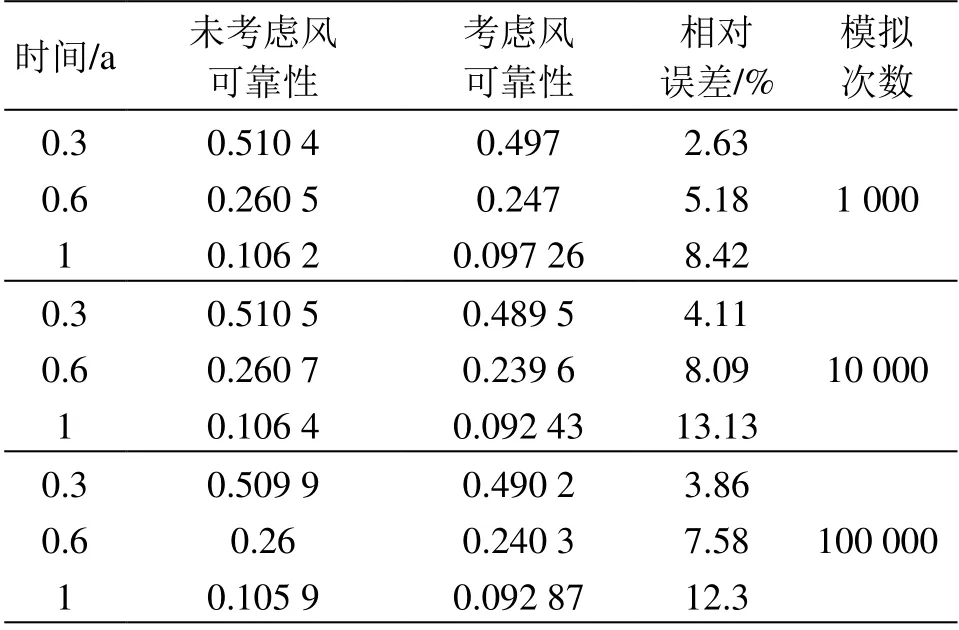
表3 接触网可靠性分析结果
由表3 可知,虽然风对接触网的影响系数因自然环境随机性的影响无法进行量化确定,但根据仿真结果可以看出,在融合了风因素之后系统的可靠性明显降低,考虑风与未考虑风的可靠性差异随着系统的运行时间不断增加也越来越大。这种情况在平均风速50 m/s,最大风速高达63 m/s 的百里风区更为严重。合理地规划接触网检修周期是预防接触网故障的重要举措,在运行一季度后接触网可靠性降至0.5 以下,此时必须对接触网进行相应的检修。
4 结语
本文采用蒙特卡洛法融合Weibull 分布模拟风速对接触网可靠性进行了分析,得出以下结论:
(1)以接触网为研究对象,证明了蒙特卡洛法可以很好地应用于接触网系统可靠性的分析;
(2)利用两参数Weibull 分布可以真实模拟出线路沿线风速;
(3)风对接触网运行可靠性的影响不可忽略,尤其是在风能比较丰富的西北大风区;
(4)提高接触网配件结构强度,合理规划接触网检修周期是预防接触网故障的重要举措。
