基于关联维数的牵引变压器励磁涌流鉴别研究
2022-11-01周启斌
李 久,周启斌
0 引言
牵引变压器在铁路供电系统中主要用作降压变压器,从电网中受电,为电动车辆馈电,是铁路供电的关键环节和重要设备,若其内部匝间短路得不到有效控制,容易造成极大的安全事故,因此要求牵引变压器差动保护具备准确识别短路故障并进行实时保护的能力[1]。励磁涌流是指变压器空载合闸时所产生的冲击电流,其与内部短路电流在波形特征上相似,简单的时域算法很难区分。
目前,牵引变压器差动保护在工程应用上均采用二次谐波识别原理,但随着技术的发展和应用材料的革新,造成励磁涌流和内部短路电流的二次谐波特征差异减小,致使二次谐波制动原理难以准确识别或判断,容易造成误动。因此,寻求新的故障特征提取方法,快速、精准判别励磁涌流和短路电流,是牵引变压器差动保护的关键问题[2]。
近年来,国内外学者提出了许多判别励磁涌流的新方法,如小波变换法、神经网络法、磁特性原理、相空间重构法、多判据的模糊逻辑法[3~7]等。由于励磁涌流本质上是因变压器铁心磁饱和而产生,其非线性特征突出,而分形理论非常适合对非线性时间序列进行分析。为此,笔者基于分形理论,对变压器不同运行状态下的差动电流信号进行分析,提取其关联维数特征信息,最终确定判据,理论上能够快速、正确识别励磁涌流和内部短路电流。
1 关联维数算法
在分形理论中,关联维数算法能够准确地映射出系统信号的内在规律,但在实际工程问题中,通常情况下是无法直接获取关联维数特征值,一般利用观测到的一维时间序列数据来间接刻画动力系统的非线性行为。
1.1 相空间重构
倘若要求取一个确定性的非线性动力系统的关联维数,首先应将监测到的该变量的时间序列进行相空间重构,得到一个新的时间序列运动轨迹,新的运动轨迹能够体现出原系统最本质的特征。
假定{xk=x(kΔt),k= 1,2,…,N}为系统中实测时间序列,将该实测数据嵌入到m维欧式空间Rm中,组成一个集合,记为

1.2 重要参数的确定
时间延迟τ和嵌入维数m是检验时间序列的重要因素,根据这两个重要参数可快速、准确计算出关联维数[8,9]。
1.2.1 时间延迟
在相空间重构过程中,选择恰当的时间延迟能够凸显出系统的动态结构,因此选取恰当的时间延迟尤为重要。在时间延迟τ的选择上,常见的方法有主周期关系法、最小交互信息标准法和自相关函数法。由于自相关函数法具有原理清晰和易于计算的优点,因此其应用最为广泛。对于τ=kτΔt的单变量离散时间序列xk,可将Rxx(τ)定义为
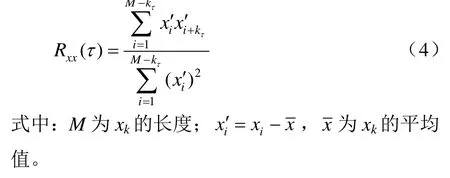
为保证快速、准确计算出关联维数,在选取时间延迟τ的问题上,既要防止样本数据之间自相交,又要保证不会丢失系统中原有信息。通常,当自相关函数满足条件Rxx(τ)<1 -e-1,则认为此时τ值基本满足要求。
1.2.2 嵌入维数
通常无法直接确定系统的嵌入维数,参照塔肯斯证明的定理:m≥2d+ 1(d为原动力系统的实际维数)可以看出,本文选取的嵌入维数通常是吸引子实际维数的2 倍以上。由于本系统的样本量不大,本文采用饱和关联维数法[10]来确定嵌入维数m。
1.3 关联维数计算
从Nm个元素中任选一个xi作为参照点,并计算xi到其他各个元素的空间距离rij,即


从式(8)可以看出,对于波形较好的周期信号,最佳状态下关联维数值为1;而不规则、粗糙的周期信号,其关联维数在1 上下变化幅值较大。
现主要考虑以下3 种可能的变压器运行状况:空载合闸、运行期间内部短路、空载合闸于内部短路。根据仿真计算得到3 种工况下各相差动电流的关联维数值D(n),考虑到各相差动电流的关联维数值D(n)分布虽然存在一定规律,但各种工况下D(n)值差异并不大,若直接以D(n)值作为故障识别的判据,存在因计算误差等干扰因素导致误判的可能性。
因此,为了放大各种工况下D(n)的差异和特征量的变化,使差动保护能更准确地识别故障类型,根据已有数据,构造了如下特征值计算方法:

式中,J(n)为各相差动电流对应的关联维数特征值。
2 三相差动电流波形及数据分析
本文利用Matlab/Simulink 进行建模仿真,以验证利用关联维数算法识别励磁涌流与内部故障电流的可行性及实用性。牵引变压器额定容量为31.5 MV·A,一二次额定变比为220/27.5/27.5 kV,参数按绕组连接方式为VX 的三相双绕组变压器参数进行设置。
2.1 空载合闸时
图1(a)所示为牵引变压器空载合闸时三相差动电流信号的波形(周期0.02 s,电流互感器的变换比1 000∶1,精度0.5 级),图1(b)所示为其关联维数特征值的变化曲线。
从图1(a)可以看出,牵引变压器空载合闸时其差动电流发生严重畸变,在波形形态上既有单侧涌流,又有对称涌流。从图1(b)可定性分析出,三相差动电流信号的关联维数特征值J(n)在各个周期内均较大,最小的为0.881,其余的特征值在1.019~3.501 范围波动。因此,牵引变压器空载合闸后的前0.2 s 内,其差动电流信号关联维数特征值的特点是数值较大和收敛性较高。
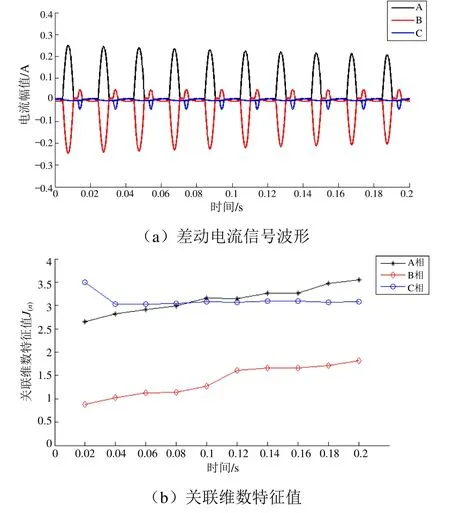
图1 牵引变压器空载合闸时
2.2 内部短路故障时
图2 所示为发生变压器内部短路故障时相关波形(C 相故障)。由图2(a)可以看出,工作状态下的牵引变压器发生内部短路故障后,其三相差动电流总体保持正弦波形态,且故障C 相的幅值接近于另一个非故障相A 相的幅值(差动取流方式所致)。图2(b)显示,关联维数特征值J(n)在各个工频周期内均小于0.55。因此,运行中的牵引变压器发生内部短路故障后的前0.2 s 内,其差动电流信号的关联维数特征值J(n)的特点是数值较小且收敛性较高。
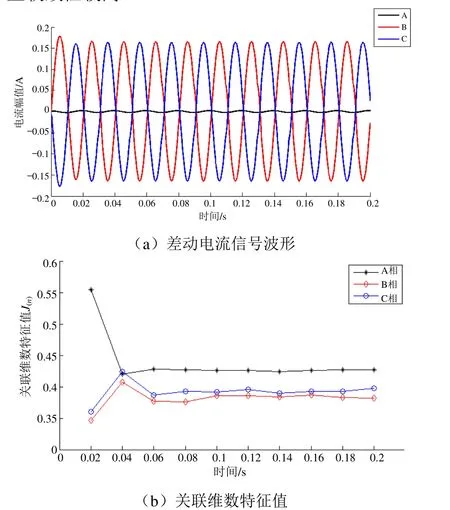
图2 变压器内部短路故障时
2.3 空载合闸于内部短路故障时
空载合闸于内部短路故障(C 相故障)时相关波形如图3 所示。从图3(a)可以看出,牵引变压器空载合闸于某单相发生内部短路故障时,励磁涌流和内部短路电流同时存在,且故障C 相和非故障B 相的差动电流的幅值较大。
从图3(b)可分析出,在前0.2 s 的各个工频周期内,非故障A 相的关联维数特征值均大于7.59,而B 相和C 相关联维数特征值均稳定在某一较小的数值,均小于0.51。因此,牵引变压器空载合闸于内部短路故障时,其差动电流信号的关联维数特征值具有一相较大而另外两相较小的特点。
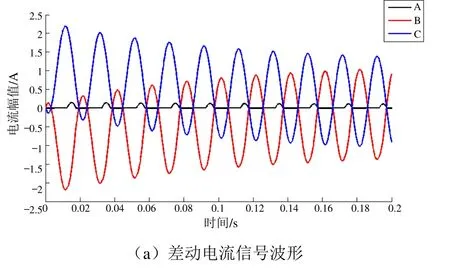
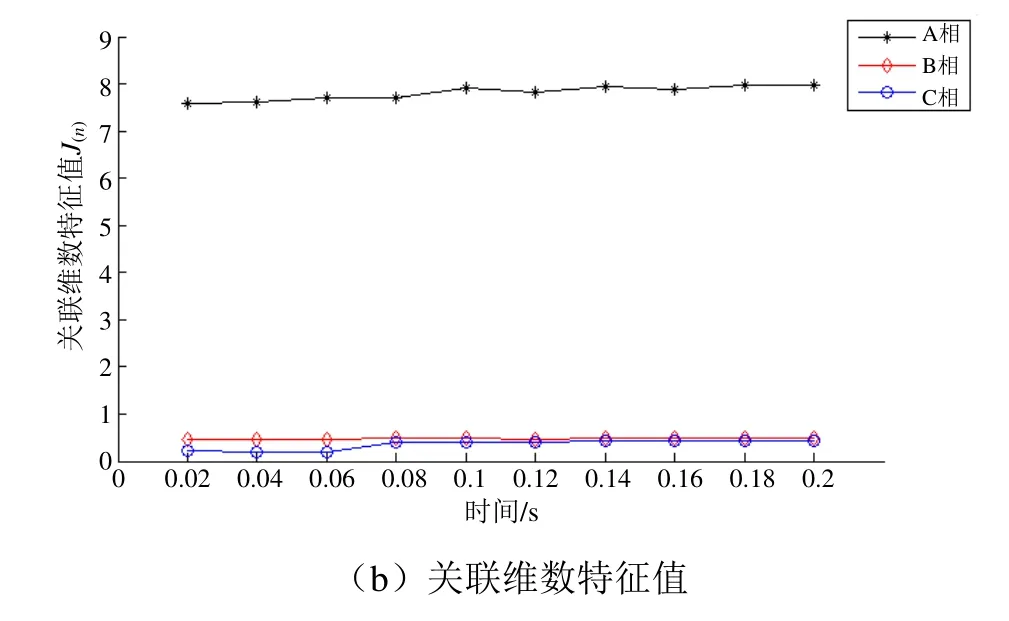
图3 空载合闸于内部短路故障时
3 差动保护综合整定分析
3.1 基于关联维数的整定分析
由于关联维数算法对数据点的要求比较复杂,而仿真得到的数据并不十分理想,故存在一些数据点偏离理论值,但基本在允许范围内。因此,在进行差动保护整定时,应充分考虑到裕量的问题。现根据上文对3 种工况下变压器各相差动电流关联维数特征值数据进行分析。
空载合闸状态下,三相差动电流关联维数特征值均较大,除第一个周期B 相的特征值为0.885 不太理想之外,其三相特征值均满足J(n)≥1.01;内部短路故障状态下时,各相特征值均较小,均满足J(n)≤0.55;空载合闸于内部故障状态下时,其中一相特征值很大,J(n)≥7.59,其他两相特征值较小,J(n)≤0.51。因此,差动保护的整定值Jset应满足在0.55~1.01 范围内取值。整定范围宽度为0.46(1.01- 0.55 = 0.46)。因此可得出以下结论:
(1)若求得三相差动电流特征值均满足J(n)>Jset,即可判定为励磁涌流,变压器保护应躲过励磁涌流而不动作;
(2)若求得三相差动电流特征值均满足J(n)<Jset,即可判定为短路电流,变压器保护应立即动作并切除故障;
(3)若求得三相差动电流特征值中一相J(n)>Jset,另外两相J(n)<Jset,即可判定为既有励磁涌流又有短路电流,变压器保护也应动作,切除故障。
如此,基于关联维数的算法即可成功实现准确区分变压器励磁涌流与内部短路电流,保证差动保护正确动作。
3.2 与现有保护算法对比
利用现有二次谐波闭锁识别算法对上述3 种运行工况的案例进行处理后,截取了前5 个周期三相差动电流二次谐波分量与基波模值比K的分布情况。
表1 截取了前5个周期空载合闸情况下各相差动电流二次谐波分量与基波模值比。
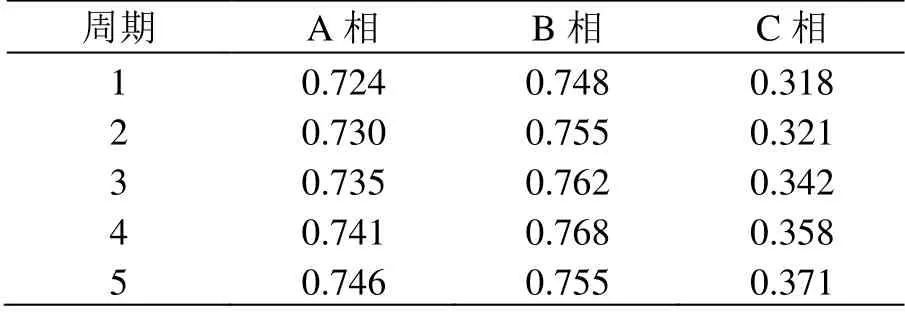
表1 空载合闸时二次谐波分量与基波模值比K
表2 截取了前5个周期内部短路故障情况下各相差动电流二次谐波分量与基波模值比。
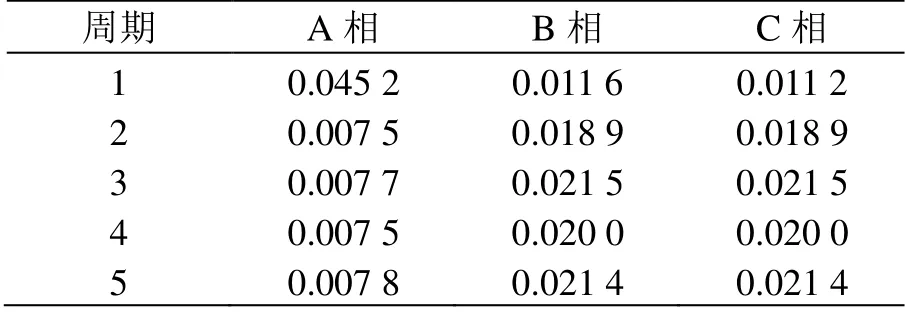
表2 内部短路故障时二次谐波分量与基波模值比K
表3 截取了前5个周期空载合闸于内部短路情况下各相差动电流二次谐波分量与基波模值比。
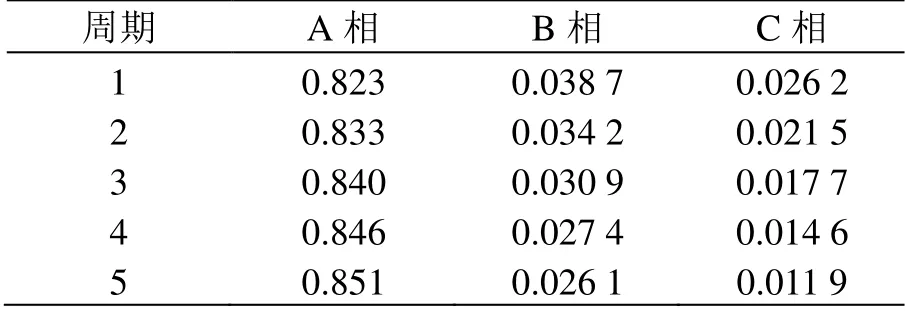
表3 合闸于内部短路时二次谐波分量与基波模值比K
由表1—表3 中数据可知:空载合闸状态下,各相差动电流二次谐波分量与基波模值比K均满足K>0.318;内部短路电流状态下,K<0.045 2;空载合闸于内部故障状态下时,A 相特征值很大,另外两相很小。由此可以判断,基于二次谐波制动原理的变压器差动保护K的取值范围为0.045 2~0.318。
基于二次谐波制动原理的变压器差动保护整定范围宽度约为0.27(0.318 - 0.045 2 = 0.272 8),为关联维数算法整定范围的59%左右。由此可知,基于二次谐波制动原理的变压器差动保护相较关联维数算法识别范围而言,整定范围小,在遇到空载合闸于内部短路情况时不能满足保护要求,同时也反映出基于关联维数算法的优越性。
4 结语
难以区分励磁涌流与内部短路电流是现有牵引变压器差动保护的主要问题,导致差动保护装置误动,降低了供电的可靠性和连续性[11]。本文主要针对励磁涌流的非正弦周期特征突出,提出了采用对非线性特征比较敏感的分形算法。通过Matlab/Simulink 仿真提取差动电流信号,分别对各相差动电流信号计算其关联维数值,并构造了特征值的计算,最后,根据分析比较变压器在各种工作状况下特征值的分布特点,建立了故障识别判据,并对差动保护进行了整定,根据判据可以准确区分励磁涌流和内部短路电流。通过与传统的二次谐波原理进行比较,体现了关联维数算法的优越性。
同时本文也存在一定的不足之处:分形的思想尚未真正应用到牵引变压器的保护中,本文所述算法在未来的工程应用中还有待进一步改进;Simulink 也无法仿真出电流互感器的实际模型,仅用电流测量模块代替,无法仿真当电流互感器饱和时的情况。分形理论还是一门新兴学科,其在工程中的应用还有巨大的发展空间,未来因变压器励磁涌流引起的差动保护的误动问题也有望得到改善。
