数控加工装备多驱动系统漏电流抑制方法

柯万宇，雷 力，汤前进，彭 瑞

(武汉华中数控股份有限公司，湖北 武汉 430223)

0 引言

近年来，现代工业迅速发展，到达了一个前所未有的高度，各种各样的工业技术与电机驱动系统已经逐渐成熟。但由于我国进入工业化的时间较短，一些先进的技术与设备系统并不完善，因此在运用上就会出现一些弊端。目前，已有大量研究人员对数控装备多驱动系统漏电流的产生原因进行研究，从根本上抑制或者减少漏电流，避免造成装备的损伤。多驱动系统主要是利用变压器的性能调整来保证电压恒定，使系统可以自动进行各个模块的调整，同时工作人员还可以随意设置装备的每个参数，不但节省了更多的资源，还能保证系统稳定运行。但由于驱动系统需要同时连接多个电源，周围的环境问题会导致输入的频率不同，当达到阈值就会自动关闭开关，强制关闭设备，造成数控加工设备断开，干扰设备的正常运行。

针对上述问题，许多学者进行了相关问题的研究，其中，郑庆杰等[1]研究了基于耦合电感的光伏逆变器漏电流抑制方法；张纯江等[2]研究了基于独立分裂电容的非隔离型中性点箝位逆变器漏电流抑制方法。上述传统抑制方法较为复杂，虽然具有一定的效果，但产生的其他影响也较为严重，致使漏电流的情况不可预计，因此，为了实现驱动系统的稳定性，本文设计一种数控加工装备多驱动系统漏电流抑制方法，期望从本质上抑制漏电流的产生，在保证系统运行的条件下及时进行反馈，降低拓扑结构的误差，提高生产效率。

1 漏电流产生原因分析及计算

抑制漏电流产生的根本目的就是要保证大地与驱动系统之间的电位差达到最小，从而使电压的变化固定在相同的频率，实质上就是通过拓扑结构转换变压器的调节模式。多次计算与调整后，只要电路中的电流与电阻的变化成反比[3]，电感尽量保持不变，即可最大程度减少装备的损伤。

变压器在运行过程中会随着桥臂的互相变换而变化，会增大漏电流的生成概率[4]，可表示为

(1)

ig为漏电流;Ci为电容；Ud为近端电压值；Us为远端电压；ti为漏电流产生的初始时间；td为结束时间。当电场中的漏电流持续增大，要立即阻断电流的产生，增大各设备表面的散热面积，并利用屏蔽板来切断电压，使其中的电容以及磁场影响达到最小，从而降低漏电流的产生概率，同时也增大了系统回路中的电阻。

假设驱动系统已经形成一个闭合回路，且其中一点接地，那么此时的电阻用R来表示，加入屏蔽板后电阻会突然变小，由于耦合层的连接作用，其他因素的干扰就会骤然增大，将电容记作为CR，电流保持不变，那么两端电压就可以表示为

(2)

要想彻底减少干扰信号的产生就要从根源上避免，确定电容与电阻的值，使信号随电压的变化而变化。当电压恒定时[5]，干扰因素达到最小，保证接地时的直流母线最短，漏电流的影响就会忽略不计，驱动系统自动维持稳定运行。

由于接入的电源不变，受到周围磁场的干扰就会限制其功率的大小，输出的电压与漏电流也会发生改变，在共模电压的基础上，增加滤过器来筛选出合适的电流大小，减少能源的浪费，进一步抑制漏电流的大小，使其在可控范围内[6]。基于变压器的转换作用，漏电流的公式可表示为

ig=icma+icmb+icmc

(3)

a、b、c为针对接地的3个电位点；icma为电源两端产生的漏电流；icmb为直流母线两端产生的漏电流；icmc为接地产生的漏电流。整个系统中最大的漏电流即为三者的和[7]，只要限制在最大值，就不会影响电路的正常流动，以此完成漏电流产生原因的分析，为后续漏电流抑制提供基础。

2 多驱动系统拓扑结构建立

由于加工装备方式有所不同，导致系统偶尔会出现漏电流情况，在以往研究的基础上，对其结构进行改进，利用电流流动方式的差异性形成一个稳定的光伏阵列，使系统直接接地[8]。基于接地电压的稳定性可以忽略电阻与功率2个参数的变化，直接计算出光伏阵列中的电流大小，然后保证其两端电压持续小于接地电压，此时多驱动系统的漏电流基本不受任何影响。驱动系统中每个设备之间都是通过自动感应电缆所连接的，因为直流电路的不断变化会使电功率波动明显，因此，只有确定光伏阵列的具体电压，才能实现电功率的多次转换[9]，那么此时形成的三路电压就可称为共模电压，以某系统为例，假设M为光伏阵列中直流电的中点，那么与电压之间的关系式为

(4)

UD为整个系统的总电压；uC为直流电与接地点之间的电压差；uP为驱动系统自身产生的电压；uL为光伏阵列中的电压值；uM为系统两端的电位差，还可将其简化为

(5)

当整个系统处于动态变化时，与直流母线存在电压差，且接地时的电位差为0，因此可以推断uM就是直流桥的共享电压[10]。根据电压变化规律可得

(6)

χ为交流电路两端电压的波长变化，且χ=2π×50；t为时间参数；UAB为任意一段的输入电压。而拓扑结构电压的变化规律公式为

(7)

将上述方程两两相加，得

(8)

uag、ubg、ucg分别为电位点的电压；uCMng为此时的共享电压；(ia+ib+ic)为3个点的电流和；Rm为电路中的电阻。那么可得

(9)

因此，拓扑电路的输入与输出的电压方程为

(10)

在电功率保持不变的前提下，使电压的数值达到最大，系统终端就会合理地调整电压的大小。

3 漏电流抑制实现

在上述多驱动系统结构设计的基础上，进行漏电流抑制。对于直流电的转换来说，采用可以调节的PWM逆变器来完成[11]，通过对电机的感应能力来获得稳定的交流电，尽可能地减少漏电流，利用特定的连接方式改变原来的驱动系统，形成共模电压[12]，可表示为

(11)

Ua、Ub和Uc为3个点两端的电压。

当电压达到一定程度时，系统就会自动控制开关，使电机呈关机状态，抑制漏电流的变大。但频率保持不变，电路电流经过逆变器后，就会与磁场相互感应，形成一个具有电流的闭合电路[13]，在多驱动系统中，电流占主要位置，电流的波动会影响驱动功能系统运行的速度，甚至会导致短路以及系统故障，使电子元件受到一定的损耗[14]，此时产生的共模电压的表达式为

(12)

Vcm1为电子元件的电压差。那么电源两端的共模电压可表示为

(13)

在共模电压的前提下，每个桥臂接收到的干扰信号会随着电压的变小而变小，使电流的值不断增大，形成一个开关电流，开关电流会抑制漏电流的增大，其大小可表示为

(14)

ihCM为开关机电流；LhT为电子元件的散热表面积。为了减小电阻，增大散热面积，可以设定一个反馈系统[15]，限制漏电流的变化，表达式为

(15)

A为损耗的能量；μr为导电率；Ωr为电阻率；f为常数。损耗的能量是由于空气中的介质所影响的，其规律符合麦克斯韦方程，即

(16)

在磁场的干扰下，方程就会变为

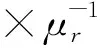
(17)

εr为误差系数；j为电缆；E(r)为能量变化；H(r)为磁场感应；λ为电磁波长度。那么在特定电场内系统的波动变化频率就可以形成一个单独的函数关系，即

g=|G1(s)|

(18)

那么通过耦合层后可得

在上述计算过程后，对漏电流进行抑制，过程如图1所示。

图1 多驱动系统漏电流抑制流程

由图1可知，当电压出现细微波动时，电流就会随之变化，同时抑制漏电流产生，保证驱动系统按照正常的模型继续运行。

4 实验对比

为验证提出的数控加工装备多驱动系统漏电流抑制方法的有效性，进行实验，并将基于耦合电感的抑制方法、基于独立分裂电容的抑制方法与本文方法进行对比，对比3种方法的漏电流抑制效果。

4.1 实验准备

实验中采用的仿真软件为Saber，实验与仿真条件为：在共模电压检测部分，电感器的共模电感为0.02 mH，并联电容为3 pF；功率变换器的开关频率为15 kHz，感应电机的额定电压为382 V，额定功率为50 Hz。逆变器样机参数如表1所示。

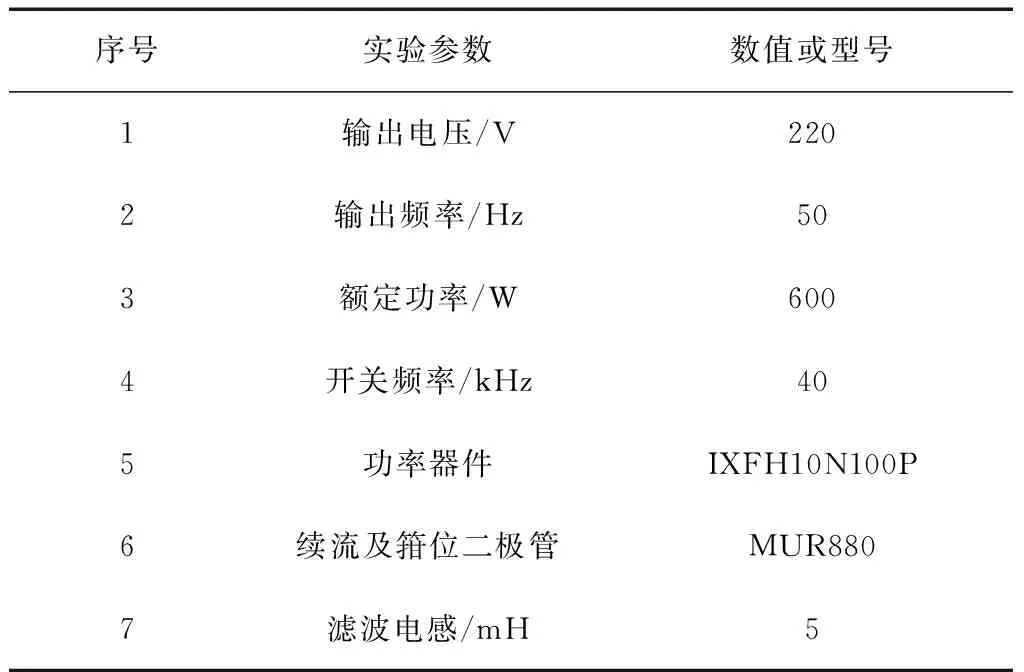
表1 逆变器样机参数

在上述实验环境下进行实验，详细结果如下所述。

4.2 漏电流抑制效果对比

分析本文方法的漏电流值，本文方法与另外2种方法的抑制效果如表2所示。

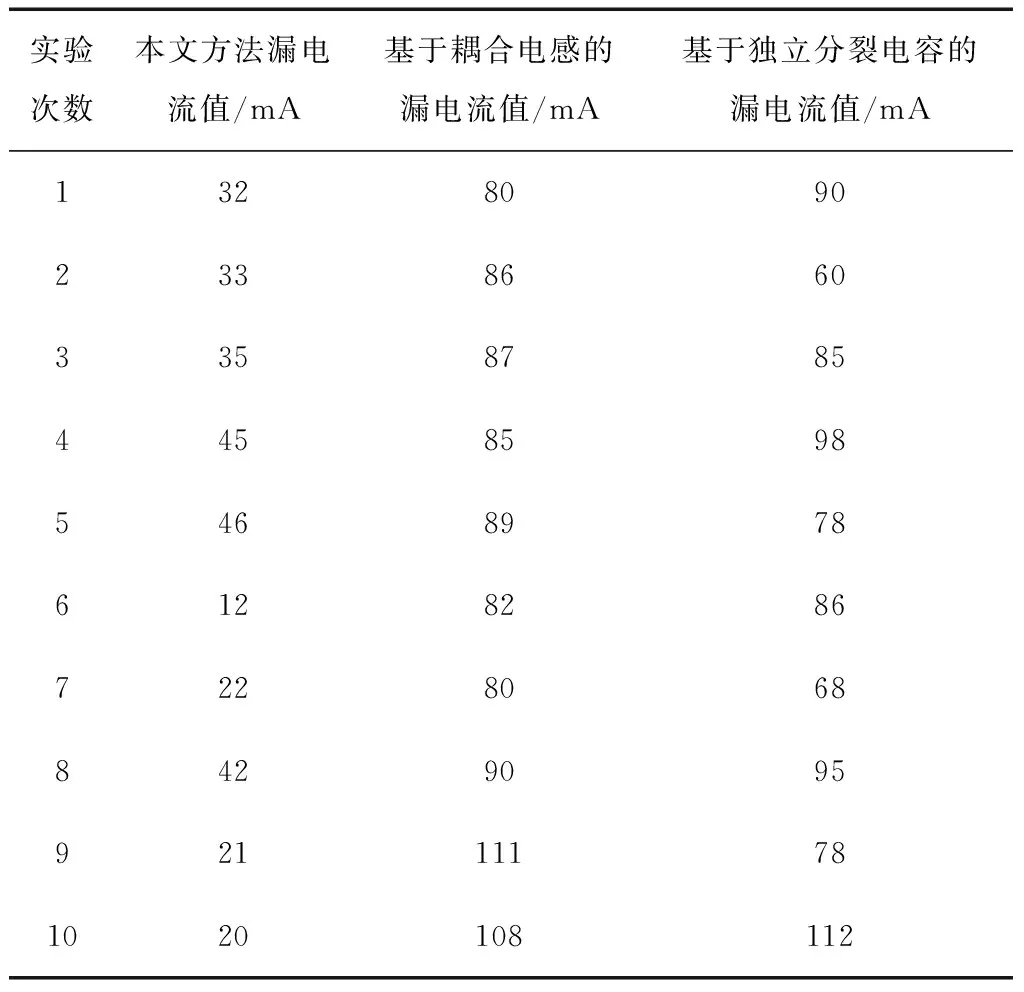
表2 漏电流值对比

由表2可知，经本文方法抑制后，漏电流较低，与另2种抑制方法相比可知，本文方法较其抑制效果好，有效降低了电流泄漏情况。

在此基础上，分析抑制过程中的漏电流振荡情况，3种波形如图2所示。

图2 电流高频部分抑制效果对比

由图2可知，采用本文方法抑制后，漏电流振荡幅度较小，有效抑制了电流中的高频部分。而另外2种方法抑制后，电流振荡幅度仍然较大，不能有效抑制电流中的高频部分。

4.3 漏电流抑制效率对比

3种方法在漏电流抑制上花费的时间如图3所示。

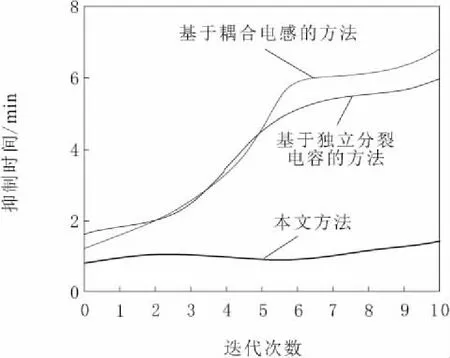
图3 漏电流抑制效率对比

由图3可知，本文方法在短时间内就能够实现漏电流抑制，较另外2种方法抑制时间少，具有较好的抑制效果。

5 结束语

本文主要针对漏电流的抑制方法进行研究，利用变频器的功能改变了原本的电机变化的频率，阻止了干扰信号的入侵，在控制电压变化的同时减少电阻，连接大地，保证闭合电路的形成。结果证明该方法简单准确，并具有较好的漏电流抑制效果。