深水板桩码头变形计算方法

李春阳，刘 洋

(中交第四航务工程勘察设计院有限公司，广东 广州 510290)

近年来，港口建设快速发展，板桩码头因具有造价低、施工速度快等优点，逐渐应用于大型化、深水化码头。由于板桩码头前墙在荷载作用下容易发生弯曲变形，对于在陆上施打板桩而后开挖港池方案，港池开挖后板桩墙即发生较大变形，致使前后轨道间距产生偏差，影响码头后续运营。特别是对自动化码头等高标准码头，结构变形还将增加运营期智能设备维护成本。因此对板桩码头结构各阶段变形的准确预测越来越受到重视，在深水板桩码头结构设计中尤为重要。

板桩码头传统计算方法主要采用经典土压力理论计算土压力，然后利用竖向弹性地基梁法进行结构计算。该方法以极限平衡理论为基础，求解特定状态下的稳定分析结果，着重于强度和稳定性计算，而忽略了土体塑性变形分析，变形的计算结果往往有较大的偏差。因此，大量学者采用有限元法对板桩码头进行数值分析。有限元方法有相对成熟和完善的理论体系，能较好地模拟施工过程，如港池开挖等卸载过程中土体与结构物的协调变形。张昊等[1]采用有限元软件ABAQUS对遮帘式板桩码头变形特性进行数值计算，并与原型观测结果进行比较；戴江山等[2]对20万吨级板桩码头结构分别采用了Robot、PLAXIS、ABAQUS等多种软件进行了位移分析；蔡正银[3]采用南水本构模型对遮帘式板桩码头和带卸荷板的板桩码头结构进行了数值模拟，对遮帘效果和卸荷效应原理进行讨论。

数值模拟分析可以反映土体复杂的应力-应变关系、结构与土体的相互作用。采用不同的单元模拟板桩、土和锚碇结构，通过激活或冻结相关网格来模拟相应的施工过程，获得不同施工阶段前墙、拉杆、锚碇结构的内力、变形。由于大多数自然土体的应力状态无法准确测量、土体的加载和卸载应力历史在实验室内无法重现，因此对于变形问题，特别是港池开挖等卸载引起的变形问题，数值模拟的计算结果往往仍与实际存在一定偏差。这是由土体的复杂性决定的，如应力-应变的非线性、加载与卸载模量差异性、应力路径与应力水平以及二者的相关性等，正确选择土体的本构模型及合理确定模型参数是数值模拟的关键所在。笔者针对实际工程案例，采用不同的土体本构模型计算变形，并对比分析计算结果。

1 土体本构模型

1.1 摩尔-库伦本构模型(MC)

MC本构模型是岩土数值分析应用最广的模型，能较好地模拟土体的强度，但简单地认为土体破坏前的应力-应变关系符合弹性虎克定律、不能考虑应力历史的影响及加载和卸载效应。

1.2 硬化土本构模型(HS)

当土体受到偏应力作用时，通常会表现出刚度下降，并发生不可逆的变形，偏应力与轴向应变曲线近似为双曲线(图1)，邓肯等据此提出了著名的非线性弹性模型”邓肯-张”模型。HS模型就是在此基础上，用双曲线拟合土的轴向应变和偏应力之间的关系：

注：qf为破坏值；Eur为卸载再加载模量。

(1)

式中：ε1为轴应变；σ1、σ3为第一、三主应力；qa为极限偏应力；q为偏应力；E50为屈服强度50%应力水平时的割线模量。

HS模型的破坏准则仍然采用MC准则，但与MC模型相比，HS模型用双曲线来表征土体轴向压缩过程中的应力-应变关系，能够表征土体的剪切硬化和体积硬化变形、弹性刚度与土体应力状态的相关性、土体卸载再加载力学性能。HS模型可以反映土体应力-应变非线性特性和复杂的应力路径，特别适合模拟加载-卸载状态下的土体变形，目前已在岩土工程中得到了广泛应用。

1.3 小应变硬化土本构模型(HSS)

HSS模型是在土体硬化模型的基础上引入了小应变属性，其理论为土体刚度与应变水平非线性相关，土体应变水平越低则刚度越高。其刚度与剪应变关系为：

(2)

式中：G为剪切模量；G0为初始剪切模量；α为系数，α=0.385；γ为剪切应变；γ0.7为剪切模量衰减到初始模量70%时对应的剪切应变，其对应关系见图2。土体的这一特性表明在小应变范围内，土体的刚度远大于接近破坏时的土体刚度，而常规土体变形试验参数均为大应变条件下获取，因此在数值计算中考虑土体小应变的特性是合理的。这是因为，不论是何种岩土工程，其变形范围总是从最大应变处逐渐扩展至应变为零的区域，也就是说始终存在小应变土体区域。因此如不考虑小应变刚度的变化特性，工程区域周边较远的土体刚度取值就会偏低，变形计算结果就会偏大。

图2 常见岩土工程问题应变范围

2 案例分析

广州南沙某码头采用钢管组合板桩结构，前墙采用直径2 m的钢管桩与Z型钢板桩组合，组合板桩上部结构为现浇C40钢筋混凝土胸墙。拉杆间距3.35 m、安装高程为0.5 m、直径为130 mm。锚碇结构采用1.0 m钢管桩组合Z型钢板桩，桩顶设C40混凝土导梁，顶高程2.0 m，锚碇桩底高程-14.0 m，前墙与锚碇结构之间分区进行水泥土搅拌桩加固处理，锚碇结构前后回填中粗砂，典型码头断面见图3。工程区域地质条件从上至下依次为淤泥-淤泥质土、黏性土、粉质黏土、中粗砂、风化岩。根据场区地质条件，施工方案为先进行大面积陆域形成及地基处理，然后对码头结构区域开挖至施工高程，进行板桩墙、锚碇墙及水泥搅拌桩施工，再安装拉杆、现浇导梁并回填，最后再分层开挖港池，待位移稳定后安装附属设施。

图3 典型码头断面

数值分析结果的准确性取决于所采用的计算参数，但数值模拟所需要的参数较多，部分参数往往难以直接从常规地质勘察报告或土工试验中获取。因此，大量学者针对复杂的土体本构模型参数与地质指标关系进行研究，并得出了许多经验公式。谢东武等[4]对小应变硬化土模型中的参数确定方法和敏感性进行分析，认为初始剪切模量可以通过剪切波速确定；王卫东等[5]根据实际工程监测数据进行数值分析反演得到了土体各模量与压缩模量的比例关系；顾晓强等[6]对小应变硬化土土体本构模型整套参数进行系统研究，建立了主要参数与土体孔隙比的经验关系。本文根据三轴试验确定各模型的强度参数，利用压缩模量、孔隙比、剪切波速，由经验公式计算各模型的刚度参数，具体参数见表1。

表1 土层参数

采用有限元软件建立三维数值分析模型，前墙和锚碇墙均采用板单元模拟，拉杆采用受拉锚杆单元，土体采用10节点四面体单元，土体和板桩墙之间设置界面单元。土体本构分别采用MC、HS、HSS本构模型。按照板桩墙-钢拉杆-回填-开挖港池的施工顺序进行模拟，有限元模型见图4。

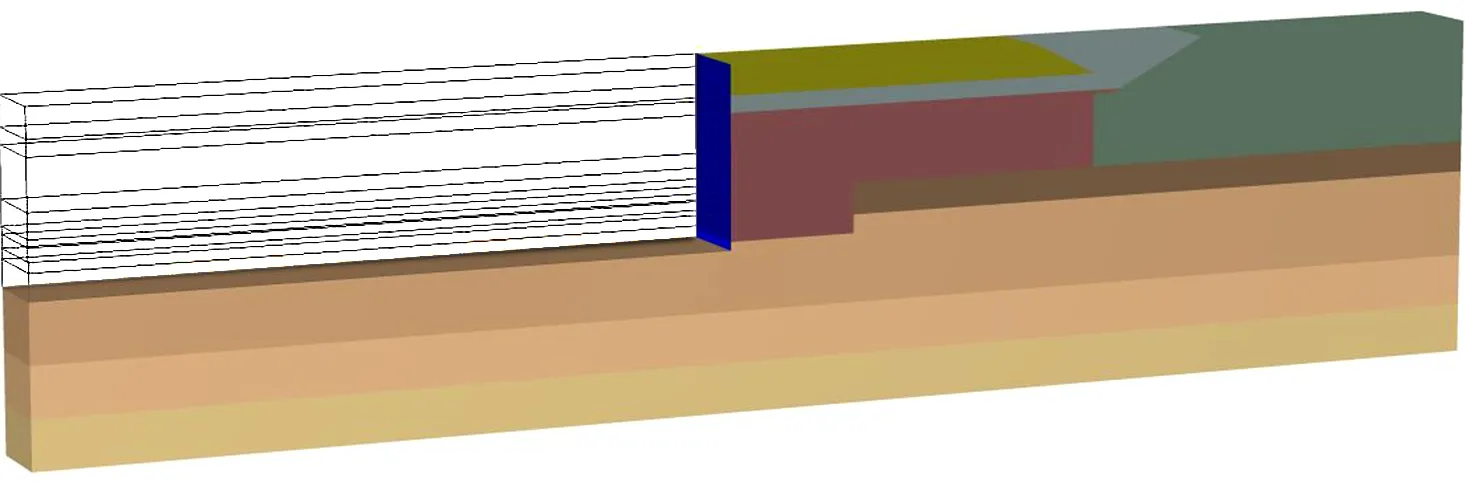
图4 岩土有限元三维模型

当港池开挖至设计底高程时，各模型位移云图见图5。计算结果表明，摩尔-库伦模型前墙最大位移为71 mm，发生在码头面；硬化土模型前墙最大位移为47 mm，发生在码头面；小应变硬化土模型前墙最大位移为34 mm，发生在码头面以下18.4 m处，码头面最大位移30 mm。码头胸墙顶面实测最大位移为24 mm，与小应变硬化土模型较为接近。

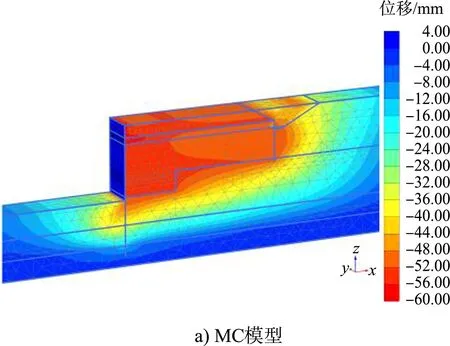
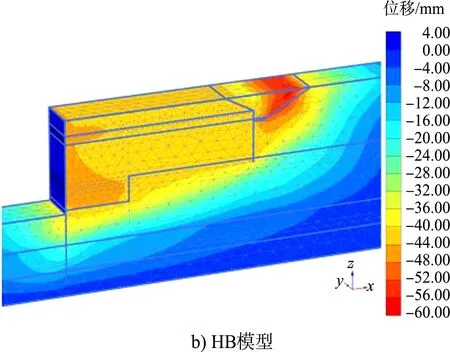
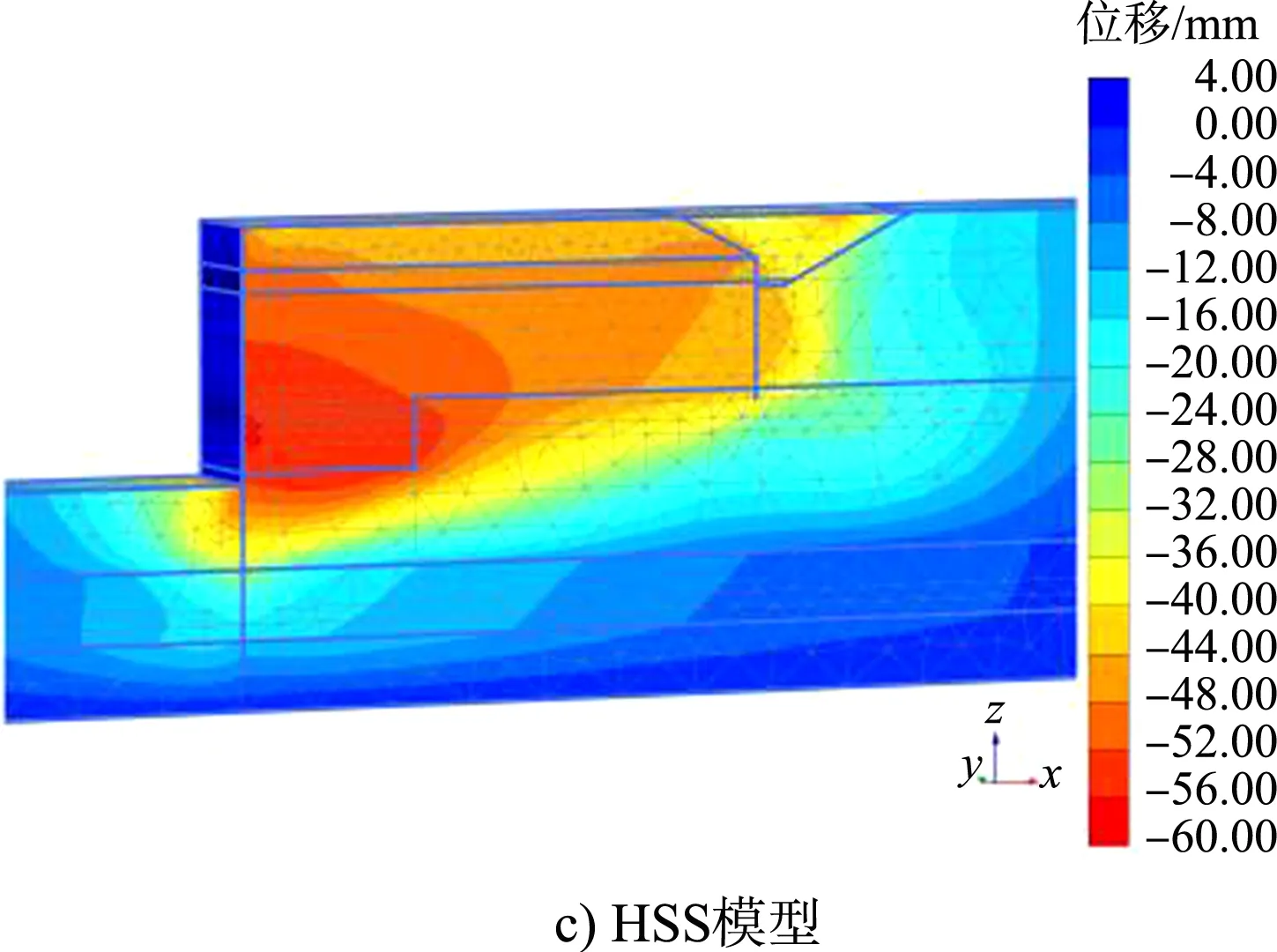
图5 码头位移云图

港池开挖至设计底高程时，由于MC模型卸载模量与加载模量相同，其港池底面隆起达101 mm。作为对比，HS模型港池底面隆起量为33mm，HSS模型港池底面隆起为29 mm，两者较为接近。MC模型未区分卸载模量，导致港池底面隆起过大，与实际情况不符，特别是对于软土地基，其卸载模量与加载模量相差较大，卸载模量与加载模量应区别对待。

3 结语

1)MC本构模型以Mohr-coulomb为屈服或破坏准则的理想弹塑性本构模型，由于未考虑卸载再加载模量，模拟结果与实测结果相差较大。

2)HS模型考虑了卸载再加载刚度及土体剪切硬化和体积硬化变形，可以较好地模拟港池开挖的施工过程，但其未能考虑外围土体在小应变情况下的刚度差异，结构变形计算结果可能偏大。

3)HSS模型在HS模型的基础上考虑了土体刚度与土体应变间的非线性关系，实测结果表明HSS构模型计算的板桩码头变形结果更为合理。