基于时频特征与排列熵的船舶噪声信号识别方法的研究

刘夏扬，李晶，*，于华鹏，赵国新，杨淑洁

(1.北京石油化工学院信息工程学院，北京 102617； 2.军事科学院国防创新研究中心，北京 100071； 3.浙江海洋大学海洋工程装备学院，浙江 舟山 316022)

船舶噪声信号的分类识别方向作为海洋勘测研究中不可或缺的技术之一，用各种神经网络对船舶噪声信号进行分类和处理的相关研究也日渐丰富[1]。能否在水下对各类目标进行快速无误地识别，很大程度上影响了未来海军舰艇的作战能力。

船只噪声信号的特征提取和分类中取得了大量高质量的研究成果[2-5]。由于声波在水中传播时，水介质的折射及声波在水面、水底的反射，自发射点至接收点存在多个传播途径的现象，船只噪声信号通常体现为时变信号[6]，且船只在行进过程中受到复杂环境的干扰，对于船舶噪声特征提取带来了一定难度。以往的船舶噪声大多都是以单一特征进行目标识别，但对于完整地表述船舶的特征信息这一要求，单一特征有部分局限性。利用不同方法对船舶信号特征进行提取，可以从不同方面反应船舶的特征。排列熵(Permutation Entropy， PE)由于其良好的鲁棒性和精确性以及能够捕获所分析的时间序列的底层动态，近年来已被应用在特征提取方面。但PE只比较相邻值，不考虑振幅，同时受等值的影响也很大，导致计算值与真实值存在偏差。为了解决这一问题，Fadlallah Bila[7]提出了加权排列熵(Weighted Permutation Entropy， WPE)，引入考虑信号波动的加权因子。与PE相比，WPE对振幅信息更敏感，能有效检测到信号的停滞区和突变区，并在许多领域得到了实际应用[8]。

长短期记忆网络(Long Short-Term Memory，LSTM)是目前实际应用中高效的序列模型，该网络对于解决循环神经网络(Recurrent Neural Network， RNN)长时序样本梯度爆炸及梯度消失的问题有着很好的效果。张亮[9]基于LSTM设计了自动区分计算机和人的图灵测试，并取得较高的识别率；Debashis Das Chakladar等[10]提出了一种基于双向长短期记忆(Bi-directional Long-Short Term Memory，BLSTM)和LSTM相结合的深度混合模型来处理脑电频谱功率分类，效果甚佳。

针对船舶噪声信号的特点，并利用排列熵对时序性信号的敏感性，笔者提出了基于时频域特征和排列熵的船舶噪声信号识别方法。利用小波新阈值去噪和希尔伯特-黄变换(Hilbert-Huang Transform，HHT)对信号进行预处理，采用反向加权排列熵对IMF进行筛选，继而将保留的IMF的加权排列熵以及瞬时频率等进行特征提取并筛选的方式得到信号特征，通过构建LSTM网络，得到了理想的分类精度。

1 基本原理

1.1 小波阈值去噪

船舶噪声信号包括机械噪声、螺旋桨噪声、水动力噪声等。为了提高后续训练速率和测试准确度，需要对信号进行预处理。

小波降噪的核心是：小波分解将原始信号分解出各层系数，给定特定阈值，系数的模大于或小于特定阈值时分别进行处理，处理完的小波系数再进行反变换重构得到降噪后的信号[11]。小波阈值去噪过程如图1所示。

图1 小波阈值去噪过程Fig.1 Flow chart of wavelet domain denoising

有用信号的小波系数幅值较大，噪声的小波系数赋值较小，选择合适的阈值处理小波系数极为重要。经典阈值函数为硬阈值函数和软阈值函数，硬阈值函数[13]：

(1)

软阈值函数：

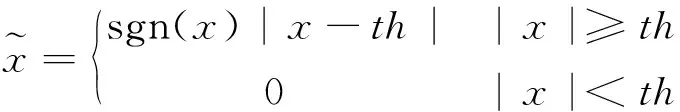
(2)

(3)

式中：n为信号长度；σ为噪声标准差。阈值可以保持局部特征，但重构信号平滑度不够。软阈值法可以得到平滑的信号曲线，但往往会使信号产生失真。采用一种新的阈值法，由Gao和Bruce引入收缩函数的变化，其克服了硬阈值和软阈值的缺点。因此具有良好的去噪性能。公式如下[14]：

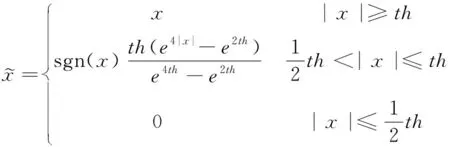
(4)

1.2 经验模态分解

由于传播过程的多途效应，往往体现的是时变信号，故在宏观上是不平稳的。为了准确描述信号特征，使用经验模态分解(Empirical Mode Decomposition， EMD)将信号分解为有限个本征模函数IMF，再求出各个IMF的瞬时频率构建特征向量组[15-18]。

EMD可以看作是一个对原始信号的筛选过程，根据原始信号的特点及规则分为多个IMF。IMF要满足以下2个条件：

(1)信号的极值点数量与零点数相等或两者数量差值为1；

(2)信号的上包络线和下包络线得到的局部均值为0.

对信号x(t)具体分解过程如下：

(1)求取原始信号的极大值点和极小值点；

(2)用样条差值法对极小值形成下包络线xd(t)，对极大值形成上包络线xu(t)，计算上下包络的均值函数公式为[15]：

(5)

(3)检查h1(t)=x(t)-m1(t)是否满足IMF的条件，如果满足则继续下一步，否则对h1(t)继续进行上面两步操作，直到第n步结果h1n(t)满足IMF条件，则可求得第1个IMF，即c1=h1n(t)；

(4)得到第1个残余函数r1(t)=x(t)-c1，接着以此类推，直到rk(t)为单调函数或者只有1个极值点为止。

(5)经过以上步骤的分解，原始信号可以表示为：

(6)

1.3 排列熵

1.3.1 加权排列熵

加权排列熵(WPE)是对排列熵(PE)的一种改进，其计算步骤如下[7]：

输入1个长度为N的时间序列X，嵌入尺寸m>2，延迟时间τ，然后从时间序列X中提取长度为m的所有可能的N-(m-1)个子序列，则X可以映射到：

=1，2，…，N-(m-1)τ

(7)

接着X按照递增顺序重新排列：

x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤…≤

x(i+(jm-1)τ)

(8)

如果有2个元素相等：

(i+(j1-1)τ)=x(i+(j2-1)τ)

(9)

则他们的顺序为：

x(i+(j1-1)τ)≤x(i+(j2-1)τ)，(j1≤j2)

(10)

计算出每个子序列的权重值ωi：

(11)

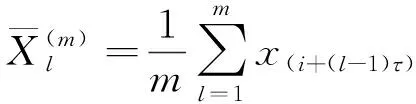
(12)

Pω(πk)=

(13)

则WPE计算式为:

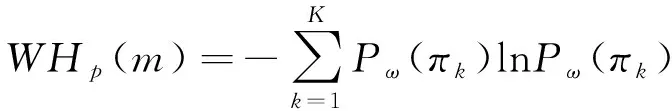
(14)

1.3.2 反向加权排列熵

反向加权排列熵(Reverse Weighted Permutation Entropy， RWPE)保持了WPE和反向排列熵(Reverse Permutation Entropy， RPE)的优势，是一种包含距离和振幅信息的复杂性度量方法，其中RPE代表时序信号与白噪声之间的距离[18]。EMD将信号分解为若干个IMF后，有效船舶信号占较大比重，但仍有部分IMF与原始信号的相关性较低，故通过计算每一个IMF的反向加权排列熵来确定每一个IMF是否包含重要信息。其定义如下[5]:

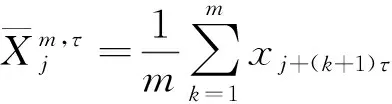
(15)

加权相对频率的计算式为：

(16)

反向加权排列熵表示观测信号与高斯白噪声之间的距离[5]，此时RWPE定义为:

(17)

其中：τ为延迟时间；m为嵌入维数；ωj为时序信号的权值。

与排列熵和加权排列熵相比，RWPE融合了振幅信息和距离信息，比PE具有更强的噪声识别能力[18]。

1.4 Hilbert变换和特征提取

对保留的IMF进行希尔伯特变换[19]：

(18)

接着构造解析信号：

zt(t)=ci(t)+jH[ci(t)]=ai(t)ejφi(t)

(19)

得到的幅值函数和相位函数分别为：

(20)

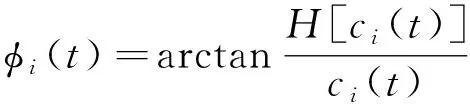
(21)

各IMF的瞬时频率计算方法为：

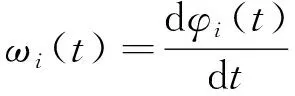
(22)

将提取的瞬时频率和瞬时幅值经过统计得到加权平均瞬时频率，其计算式为：

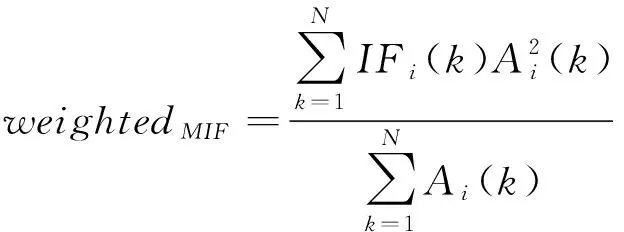
(23)

式中：IFi(k)为第i个IMF中第k个点的瞬时频率；Ai(k)表示第i个IMF中第k个点的瞬时振幅。

1.5 长短期记忆网络

利用长短期记忆算法对预处理后的信号进行分类训练。LSTM是在RNN的基础上增加了一个单元状态C。

LSTM记忆单元组织图如图2所示。

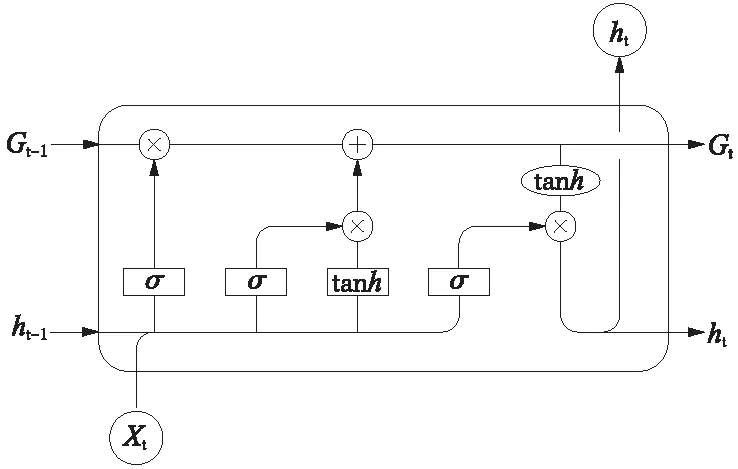
图2 LSTM记忆单元组织图Fig.2 Chart of Memory Cells of LSTM

由图2可知，在T时刻，LSTM的输入有3个：上一时刻的输出值ht-1、上一时刻的单元状态Ct-1以及当前网络的输入值xt；输出有2个：t时刻的输出值ht和当前时刻的单元状态Ct。在t时刻，输入门和输出门都是关闭状态，于是记忆单元把之前的状态传递到t+1时刻，这样就把第1个状态记录了下来。以此类推，时间步t时的记忆单元就被记录了下来，解决了梯度消失的问题。

以上为单向LSTM的计算方式，其相比单向LSTM，双向LSTM的隐藏层要保存2个单元状态A、A′，A参与正向计算，A′参与反向计算，最终的输出y取决于2个值。双向LSTM的训练单元如图3所示。

图 3 双向LSTM训练单元Fig.3 Training Unit of BILSTM

利用双向LSTM进行训练，相比单向LSTM训练精度更好。

2 实验分析

2.1 实验概述

按照上述理论分析，船舶噪声信号分类识别总体流程如图4所示。

图4 分类识别总体流程Fig.4 Flow chart of classification and identification

2.2 数据来源及预处理

为了验证船舶噪声识别方法的有效性，使用了维戈大学提供的名为ShipsEar的真实水下船只噪声数据库。

实验涉及四类船只目标，简称为A、B、C、D类，2 000个噪声样本作为实验数据集。每个样本分别采集于不同时间和环境，信号采样率为50 kHz。选取的各类数据的原始时域波形如图5所示。

图5 四类信号类时域分析图Fig.5 Four Class time domain waveform

为验证新阈值的去噪能力，将原始信号视为未加噪声信号x(t)，加噪信号由原始信号和白噪声叠加，信噪比为10 dB。利用小波变换将x(t)划分为4阶小波信号，sym4作为小波函数，并使用新阈值函数去噪。最后，将去噪后小波信号进行组合得到去噪后的信号s(t)。原始信号与去噪信号如图6所示。以信噪比和均方根误差来评价去噪效果。信噪比的计算式为：

(31)

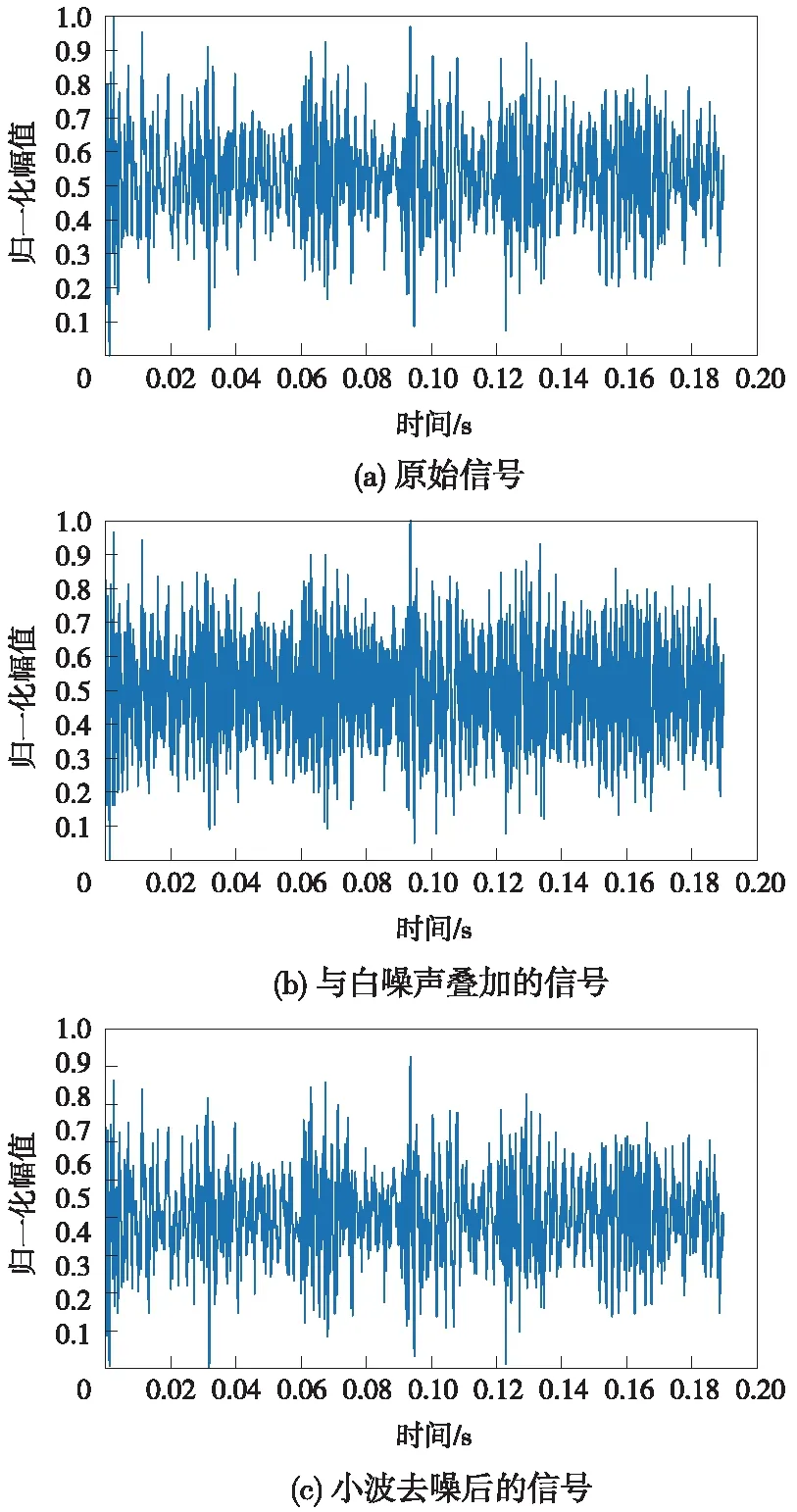
图6 原始信号与去噪信号Fig.6 Original signal and denoised signal

不同阈值方法的去噪能力如表1所示。

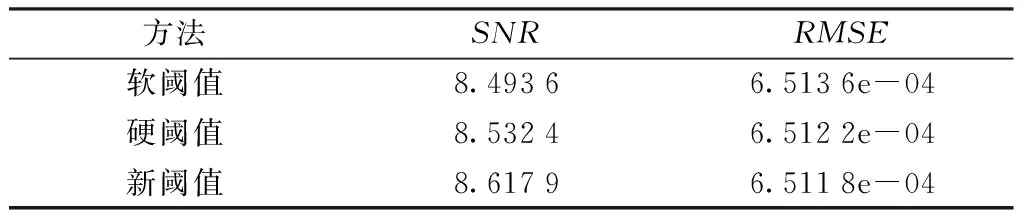
表1 不同阈值方法去噪能力比较

从表1中可以看出，新阈值法在保持较低RMSE值的同时，可以得到较高的信噪比。故新阈值法去噪性能更佳。某一信号去噪前后EMD分解图如图7所示。

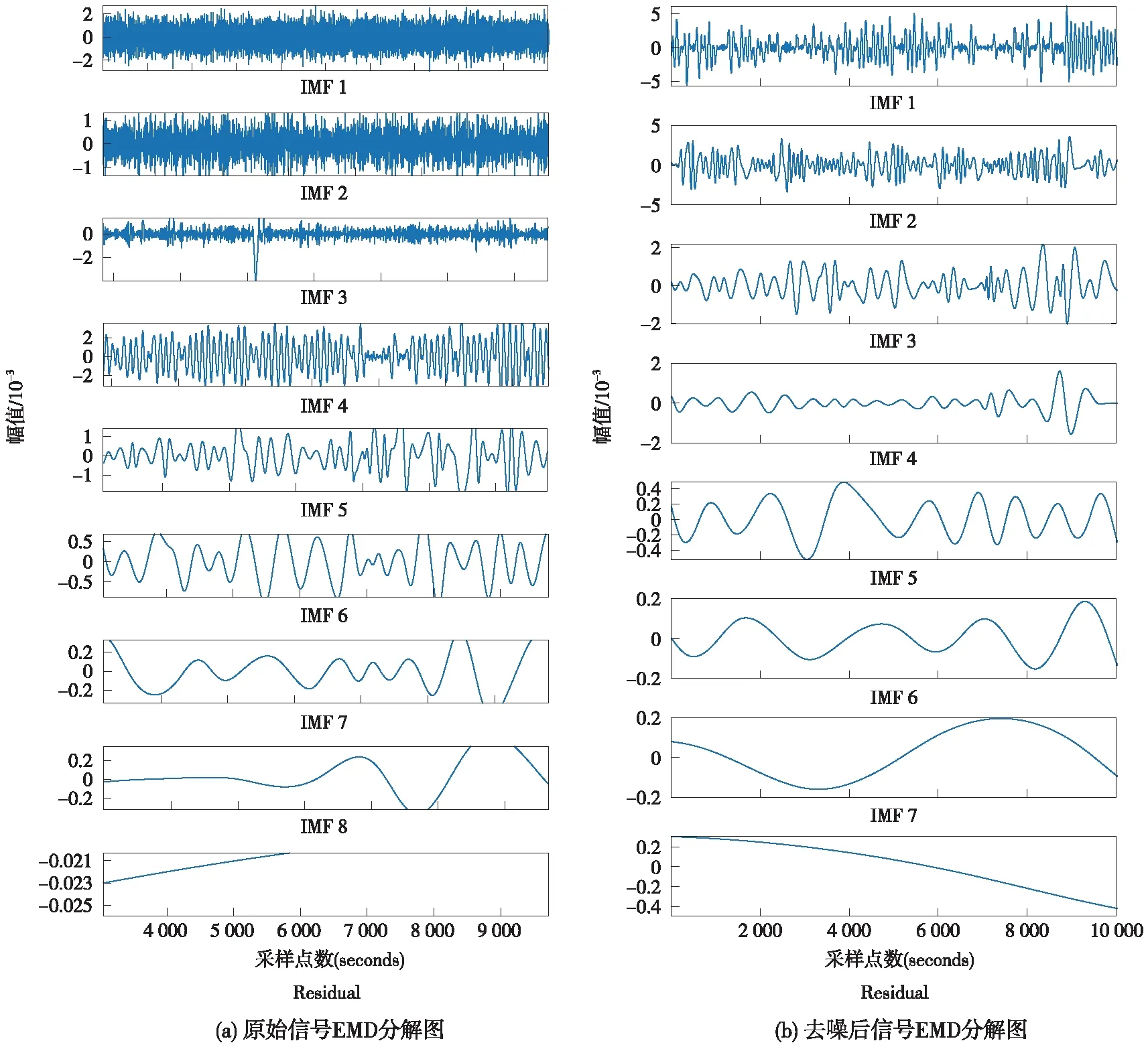
图7 原始信号和除噪后EMD分解对比图Fig.7 Comparison between the EMD decomposition of original signal and the original signal after denoising

在经过信号分解算法处理的有噪信号得到的IMF中，并不是每个IMF都能对原始信号进行表征。有些成分是噪声，需要在特征提取前排除。由文献[18]可知，RWPE值越大，观测值与白噪声的距离越小。四类信号在求取IMF后每一类随机选取100组IMF信号求RWPE平均值。四类船只信号中IMF的RWPE结果直方图如图8所示。该去噪方法区分原始信号中噪声IMF是可行的。为了进一步验证该方法的有效性，选取RWPE阈值为2和4的本征函数重构新信号。不同取值下加噪信号和重构信号的信噪比如表2所示。加噪信号的信噪比为10 dB。从表2中可以看出，当RWPE取值为4时，可以得到较高的信噪比。

表2 不同RWPE值下原始信号与重构信号的信噪比

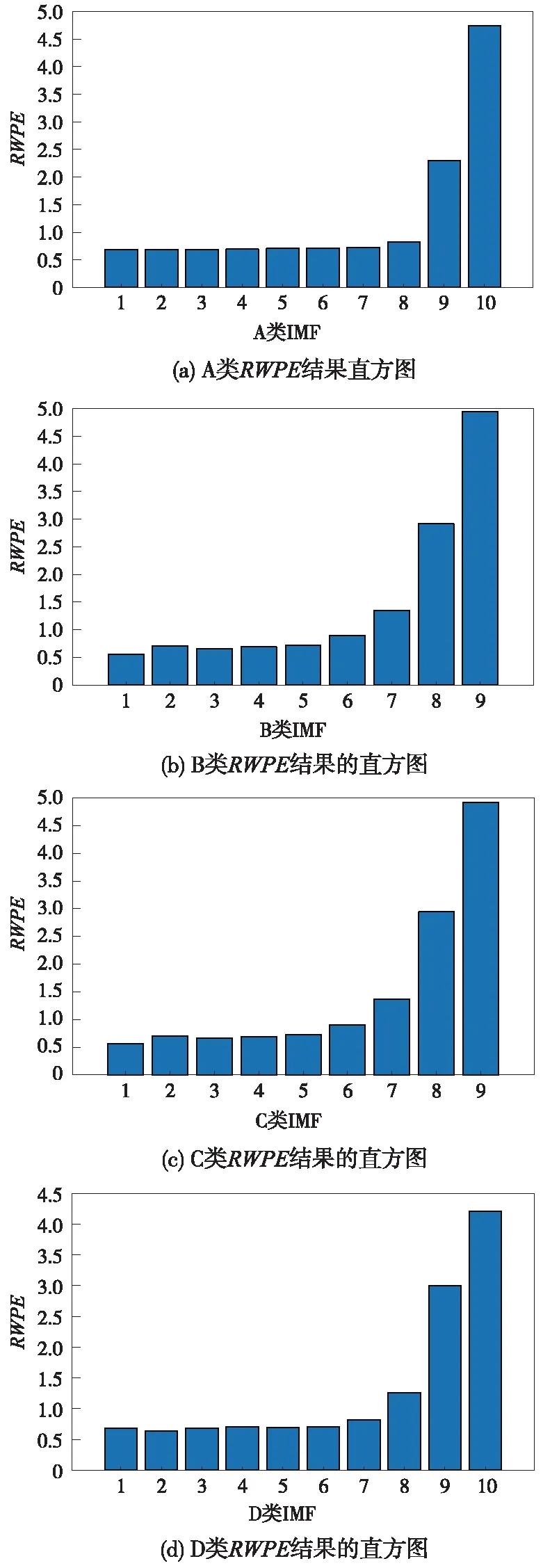
图8 EMD的RWPE结果的直方图Fig.8 The histogram of the RWPE results for EMD

2.3 船舶噪声信号识别

从数据集中随机选出80%的信号作为训练集，在训练前使用训练集的均值和标准差来标准化训练集和测试集。由于输入信号各有2个维度，将输入序列大小设置为2；指定双向LSTM层输出大小为500；每次训练迭代的小批量的数量设置为50；最大训练次数设置为50。

3 分析与讨论

为了进一步检验特征提取方法的性能，选用IMF与原始信号的能量比以及WPE加权能量比构建特征向量[25]，进行分类实验。

处理后的结果对应的识别结果如表3所示， 目标识别的结果混淆矩阵如图9所示。

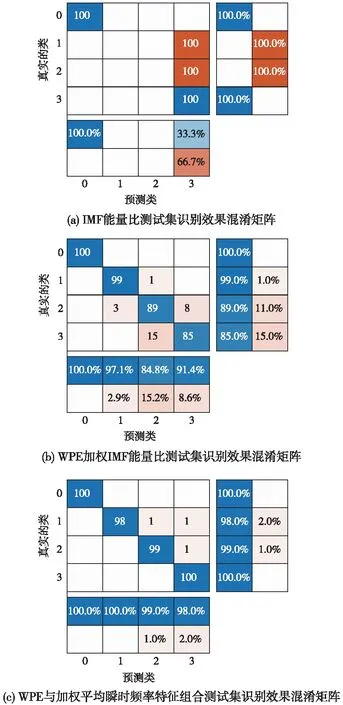
图9 测试集效果混淆矩阵Fig.9 Test set classification effect of confusion matrix of Class A、B、C、D

表3 不同特征提取方法识别率对比

由表3中可以看出，以IMF和原始信号能量比为特征进行识别在多类的情况下并不实用，平均识别率为50%。在相同样本的情况下，利用WPE对能量比进行加权后作为特征进行训练，系统的平均识别率提升到92.12%，而特征提取方法训练后的平均识别率为99.40%，说明提出的特征具有更好的性能。

使用提出的特征提取方法，A类船只的识别率达到100.0%，B类船只的识别率为99.3%，C类船只的识别率为98.5%，D类船只的识别率为99.8%。故对于船舶噪声识别的效果是比较理想的。

4 结论

提出了一种基于时频域特征与排列熵的识别方法，经验模态分解可以根据局部特征将多分量信号分解为一系列的IMF，并利用原始信号的时频域特征有效提取船舶噪声特征，并利用加权排列熵与加权平均瞬时频率组成特征向量，并利用LSTM对不同类型的船舶噪声信号进行识别。分析了不同特征识别的特点，并通过实验证明了该方法的可行性。