基于弹性梯度下降模型的神经网络遥感水深反演

2宿殿鹏2王贤昆郭亚栋李劭禹

(1.山东科技大学 测绘与空间信息学院，山东 青岛 266590；2.自然资源部 海洋测绘重点实验室，山东 青岛 266590)

水下地形地貌信息的获取是海岸带管理、海洋资源开发等应用的基础。近年来，随着回声测深、激光雷达技术的发展，水底三维地形地貌数据的获取手段越来越多样化[1]。然而，船载回声测深无法获取浅水及存在岛礁、暗礁等船只不易到达的复杂地形区域的信息；机载测深雷达技术虽然可以获取浅水区域的信息，但其风险大、成本高[2]。此外，现阶段对于浅海岛礁水深探测，两种技术在成本控制、测量效率、测量广域性方面存在一定的局限性，而遥感水深反演技术则可以作为一种补充[3]。

从20世纪70年代起，利用卫星遥感影像进行“快速、大范围、实时”的水深反演逐渐成为研究的热点之一。现有的水深反演模型主要分为3类：理论解析模型、半理论半经验模型和统计相关模型[4]。理论解析模型利用辐射传输方程，通过测量水体内部的光学参数计算水深。Lyzenga等[5]利用双层流假设，简化经典辐射方程并忽略了水体内部的反射效应，得到浅水区由水面出射的光反射和水深之间的关系。但由于该模型求解繁琐，水体光学参数难以获得，没有得到广泛应用。半理论半经验模型根据光在水体中的辐射衰减，采用理论模型和经验参数相结合的方式实现水深反演[6]。Benny等[7]在考虑水体底部反射光衰减的基础上，提出一种单波段水深反演算法，但算法对水质及水底底质要求较高。统计相关模型通过建立遥感图像光谱特征值和实测水深值之间的关系获得水深信息[8-9]。与理论解析模型和半理论半经验模型相比，统计相关模型无需水体内部光学参数，计算较为简单[10]。Setiawan等[11]提出一种利用随机森林提取水深信息的方法。该方法假设水深和辐射强度之间存在非线性关系，通过建立辐射强度和实测水深之间的关系得到水深值。

近年来，机器学习算法及高分辨率卫星数据在水深反演方面得到广泛应用[12-15]。林位衡等[16]利用水深信息和多光谱图像辐射亮度之间的相关性建立了基于粒子群优化的BP(back propagation)人工神经网络模型，反演出珊瑚环礁附近浅海区的水深，认为人工神经网络方法在水深反演方面优于传统的统计方法；韩中含等[17]利用多光谱影像反演水深，通过对半理论半经验模型和BP神经网络模型进行对比分析，发现BP神经网络模型虽然在反演精度方面优于传统模型，但该模型易陷入局部最优。

传统BP神经网络模型[18]在进行权值更新时，依赖于学习速率和动量项的设置，在学习过程中会出现“模糊自适应”问题，导致收敛速度慢，且依赖于偏导数的大小，易出现局部最优。本研究提出一种基于弹性梯度下降模型对BP神经网络进行优化的遥感水深反演算法。该算法在权值更新时，不考虑偏导数的大小，直接对权值更新值进行局部自适应改变，减少学习率和动量项参数的计算，加快了收敛速度[19]，且误差平缓下降，易于收敛。最后通过南海实验数据对其反演效果进行验证。

1 弹性梯度下降水深反演算法

提出一种基于弹性梯度下降模型的神经网络水深反演算法，利用弹性梯度模型，对传统BP神经网络算法进行优化，以解决传统BP神经网络模型存在的收敛速度慢、权值更新模糊自适应的问题。

1.1 数据预处理

对所获取的遥感图像进行辐射定标、大气校正和几何校正处理，以消除大气和光照等因素对地物反射的影响及因光折射等带来的几何畸变影响，获得地物真实的辐射率、反射率和位置信息。对多波束测深数据则要进行测深校正，以还原图像获取时刻的真实水深。

1) 辐射定标

辐射定标是将遥感影像上无量纲的灰度值(digital number，DN值)转换为大气外表层反射率(辐射亮度)的过程，其转换式如下：

L(λi)=gaini×DNi+offseti。

(1)

式中：L(λi)为第i波段的辐射亮度值,W/(m2·sr·μm)；DNi为第i波段图像像元灰度值；gaini和offseti分别是第i波段的增益值和偏移值。辐射定标后图像像素值为辐射亮度值，为大气校正提供参考。本研究依据卫星图像头文件中提供的增益值和偏移值，按式(1)对遥感图像进行辐射定标。

2) 大气校正

大气的衰减作用对不同波长的光是有选择性的，因而大气对不同波段影像的影响不同，大气校正可以去除大气散射、气溶胶等影响，尽可能还原地表真实反射率。本研究利用ENVI软件中的FLAASH大气校正工具进行大气校正。

3) 几何校正

大气折射、地形起伏等因素可能导致原始图像上地物的几何位置、形状等特征在参考系统下发生一定的形变，因此通过数学模型来消除成像时的一些形变。本研究利用卫星自带的地理定位文件进行几何校正。

4) 测深校正及测深点提取

为了保证水深数据的精确度，要对多波束实测水深数据进行潮汐校正，把实测水深数据(Dt1)校正到遥感影像获取时刻的水深值(Dt2)。水深数据潮汐校正模型如式(2)所示。

Dt2=Dt1-Tt1+Tt2。

(2)

式中：Dt1、Dt2分别为t1和t2时刻的水深值；Tt1、Tt2分别为t1和t2时刻的潮汐值，可通过西沙群岛潮汐表查询并通过潮汐公式[20]计算得到；t1、t2 分别为实测水深时间和遥感影像获取时间。测深点提取则是对多波束数据进行抽稀及剪切，得到所选区域的测深点数据。

1.2 弹性梯度下降模型

弹性梯度下降模型[19]是一种高效的神经网络学习方法，根据误差函数的行为对权值的更新进行局部自适应学习。同传统的梯度下降法相比，弹性梯度下降法计算量小，网络的收敛时间短。弹性梯度下降算法BP神经网络主要由正向传播过程和误差的反向传播过程组成。其中，正向传播算法与传统BP算法一致，而反向传播算法传播过程分为两步：一是调整步长，二是根据步长调整权重。

1) 正向传播

BP神经网络正向传播如图1所示，输入层的神经元接受来自外界的输入p并传递给隐含层神经元，依据式(3)和(4)逐层进行计算，最后传递到输出层。

图1 正向传播示意图Fig. 1 Schematic diagram of forward propagation

图1中，p为BP神经网络的样本输入，ωi为第i层的连接权值，bi为第i层偏置值，∑为累加器，ni为第i层累加值，fi为第i层传播函数，φi为第i层的输出(当位于第一层，φi=p)，故有：

ni=wiφi-1+bi，

(3)

φi=fi(wiφi-1+bi)。

(4)

2) 反向传播(权值更新)

在误差反向传播过程中，计算实际输出值与模型计算输出值之差E，应用链式法则[20]计算网络中每个权重对误差E的影响：

(5)

式中：wij是从神经元j到神经元i的权重；φi是输出；ni是神经元i的输入的加权和。当每个权重的偏导数已知，通过进行简单的梯度下降就可以达到最小化误差函数的目的：

(6)

显然，对偏导数进行缩放的学习率ε的选择，影响达到收敛所需的时间。如果ε设置的过小，则需要过多的步骤才能实现误差降低，过大则可能使误差下降出现震荡，跳过误差的最小值。

早期的解决方法是引入动量项：

(7)

式中动量参数μ缩放了上一步的权重变化对当前权重变化的影响。动量项被认为使学习过程更加稳定，并加速误差函数浅区域的收敛。然而，动量参数μ的最优值和学习率ε的选择具有相同的问题。

大多数全局和局部自适应算法都根据误差函数的变化对学习率进行改变[21]，而实际采用的加权步长wij的大小不仅取决于(自适应)学习速率，而且还依赖于偏导数。因此，为避免“模糊自适应问题”弹性梯度算法直接改变权重更新值的大小而不考虑偏导数的大小，为每个权重引入单独更新值δij来决定权重更新的大小。该自适应更新值在学习过程中根据误差偏导数的改变而改变，其学习规则如下。

(8)

式中0<η-<1<η+。适应规则的原理为：当相应权值wij的偏导数改变其符号时，表明上一次的更新值过大，跳过了一个局部最小值，更新值会乘一个降低因子η-；如果偏导数符号不变，则更新值会乘以增加因子η+，以加速收敛。若更新值与上一时刻相同，则无需改变。

在调整了每个权重的更新值之后，权重的本身遵循一个简单的规则：如果偏导数为正，则权重按其更新值减少；如果偏导数为负，则按其更新值增加。即：

图2 反演流程Fig. 2 Inversion process

(9)

(10)

3) 参数设置

反演开始时，所有的更新值δij都被设置为初始值δ0。因为δ0直接决定了第一个权重步长的大小，较好的选择是δ0=0.1，更新值的范围限制在上限δmax=50，下限δmin=1×e-6，以避免变量变化过大或过小。通过将最大更新值设置为相当小的值(例如，δmax=1)，可以达到误差平滑减小的结果。η-和η+的选择由以下因素决定：如果跳过最小值，则前面的更新值太大。所以平均来说，将更新值减半，即η-=0.5。一方面，增加η+因子必须足够大，以允许更新值在误差函数区域中快速增加；另一方面，如果增加的因子太大会导致权重步长方向持续变化，学习过程受到干扰。因此，为了使参数选择更简单，固定η+=1.2和η-=0.5。

1.3 反演流程

基于弹性梯度下降模型的BP神经网络遥感水深反演流程如图2所示。算法的具体步骤为：

1) 对数据进行预处理，对多光谱影像进行几何校正、辐射校正和大气校正，将影像的亮度值转换为地物真实的反射率值，进行光谱特征的提取。再进行多波束测深数据测深校正，提取水深点。

2) 进行模型训练，提取对应的光谱特征值和水深值，将光谱特征值加入模型输入端，依据弹性梯度下降原理对模型的参数进行更新，以达到误差最小化。

3) 将测试数据导入训练好的模型中，计算预测的水深值。

2 实验与分析

2.1 研究区域

为验证算法的有效性，选择中国南海西沙群岛永乐环礁的甘泉岛为研究区域，面积约为0.3 km2，中心位于北纬16°32′18″，东经111°35′10″，岛呈椭圆形，环岛周围水深较浅，水体清澈，底质单一，适合进行光学遥感水深反演实验。如图3所示，红色框选为甘泉岛区域。

图3 甘泉岛区域Fig. 3 Ganquan Island area

遥感数据采用GeoEye-1卫星所拍摄的影像数据，采集时间为2013年2月18日。GeoEye-1卫星能以0.41 m黑白(全色)分辨率和1.65 m彩色(多光谱)分辨率拍摄图像。其多光谱影像包括红、绿、蓝、近红外4个波段，具体参数如表1所示。

表1 GeoEye-1卫星遥感数据参数Tab. 1 GeoEye-1 satellite remote sensing data parameters

实测水深数据采用甘泉岛附近的船载多波束测深数据，该数据已校正至深度基准面，经过重采样处理后其空间分辨率为2 m，测深精度为0.2 m，测点分布较为均匀，精度较高，适合用来进行水深反演。图4为研究区域经裁剪后的卫星影像(图4(a))和多波束测深点(图4(b))。

2.2 数据预处理结果

利用ENVI软件对遥感图像数据进行辐射定标、大气校正、几何校正，利用归一化水指数(normalized difference water index，NDWI)对图像进行水陆分割，从处理后的图像中提取红、绿、蓝、近红外4个标准波段的反射率，各波段具体的反射率值范围如表2所示。在研究区域，海水在蓝波段和绿波段的反射率值最高，而在红波段和近红外波段的反射率值相对较低，符合海水在可见光波段的反射特性。

图4 卫星影像及多波束测深点Fig. 4 Satellite images and multi-beam sounding points

图5 采样点分布Fig. 5 Distribution of sampling points

表2 研究区域各波段反射率值范围Tab. 2 Range of reflectance values of each band in the study area

进行多波束数据点和遥感图像像元的匹配，提取点对应的光谱值。选取甘泉岛部分区域进行研究，选取926个点，水深0～25 m，其中648个点用于模型训练，278个点用于模型精度检验。如图5所示为采样点分布。

利用皮尔森相关系数作为度量各波段反射率值和波段比值与实际水深的相关标准，其计算式为：

(11)

式中，r为皮尔森相关系数，Xi代表第i个点处光谱因子的值，Yi代表与其对应的水深值，n为采样点的个数。皮尔森相关系数取值范围为|r|<1，其中：|r|≥0.8时，两变量间高度相关；0.3≤|r|<0.8时，两变量中度相关；|r|<0.3时，两变量不相关。

经过计算得到各个反演因子和水深值之间的相关系数，具体如表3，B1、B2、B3、B4分别代表多光谱波段中的蓝、绿、红和近红外波段的反射率值。

为直观展示各个波段反射率值与水深之间的相关性，绘制柱状图如图6所示。

表3 水深反演因子和水深值相关系数表Tab. 3 Correlation coefficients of water depth inversion factors and water depth values

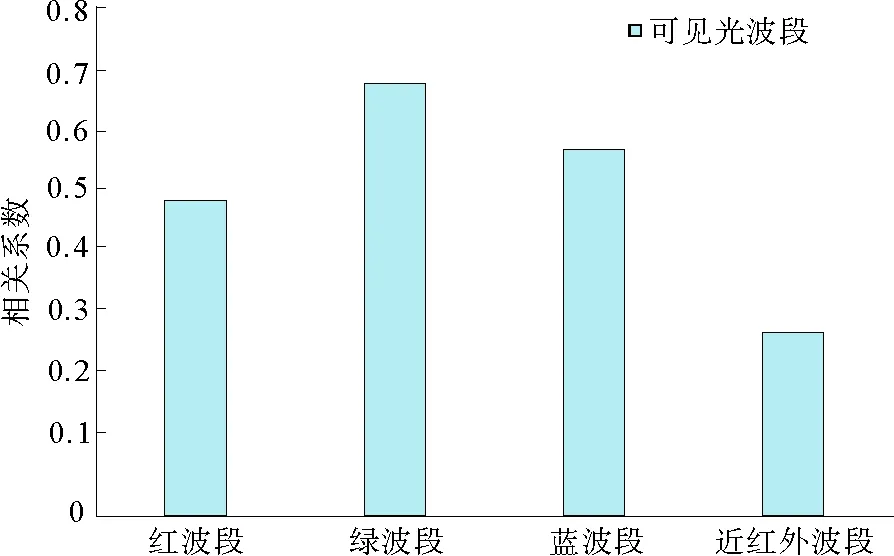
图6 各波段反射率和水深相关性Fig. 6 Correlation between reflectivity and water depth in each band

由表3和图6可知，蓝、绿波段的反射率比值和水深之间呈高度相关性，蓝、绿、红波段反射率及蓝和近红外、绿和近红外、红和近红外波段反射率比值和水深值为中度相关，而近红外波段反射率及绿和红、蓝和红波段反射率比值和水深之间基本不相关。将高度相关和中度相关的光谱因子作为模型输入因子。

2.3 水深反演性能分析

为了定量评估算法的性能，分别计算迭代次数、决定系数R2、均方根误差(root mean square error，RMSE)和平均绝对误差(mean absolute error，MAE)4个指标来评估反演效果。将本算法与传统的BP神经网络算法进行对比。

1) 精度评价指标

拟合优度是指回归直线对观测值的拟合程度，拟合优度的统计量决定系数R2，其最大值为1，R2的值越接近1说明回归直线的拟合程度越好；反之，R2的值越小，说明回归直线对观测值的拟合程度差。采用均方根误差RMSE、平均绝对误差MAE，作为水深反演精度指标。

R2的计算式为：

(12)

RMSE的计算式为：

(13)

MAE的计算式为：

(14)

式(13)～(14)中，Δzi=Yi-yi为第i个检查点实测水深值和反演水深值之间的差值，Yi为第i个检查点的多波束测深值，yi为第i个检查点的反演水深值，n为所选检查点的个数。

2) 反演效率及精度评价

为检验基于弹性梯度下降BP神经网络模型水深反演结果的精度，计算未参与模型构建的278个测试点位的水深值，对比测试点位的水深值和多波束实测水深值之间的误差。模型训练所采用的参数设置为：输入为7个反演因子；中间层的数目依据反复实验确定为15个；输出层为水深值。输入层和中间层的激活函数均为Sigmoid函数，输出层的函数为线性函数，终止阈值依据反复实验得出适合本实验样本的最佳值为0.01，最大循环次数考虑误差达到中止阈值时所进行的最大循环次数，故将其设置的足够大，为20 000。改进前后对比结果如表4所示。

表4 反演模型精度及迭代次数对比Tab. 4 Comparison of the accuracy of the inversion model and the number of iterations

由表4可知，相比于传统BP神经网络模型，改进后的模型所反演水深的R2增大0.007，RMSE减小了0.296 m，MAE减小0.207 m，迭代次数比传统的BP神经网络模型减少5 190次，改进后的算法在达到终止阈值时所消耗的时间降低了34 s。因此，较传统算法，所提算法水深反演精度和反演效率均得到明显的提升。

为了更直观地展示两种模型水深反演的精度，进行拟合散点图对比，结果如图7所示。

图7 拟合散点图Fig. 7 Fitted scatter plot

从散点图拟合的趋势线来看，改进后的神经网络模型的拟合程度较好，在20～25 m水深段的改进效果最好，其拟合程度也最高，散点均匀分布于拟合曲线两侧。

将验证数据按水深划分为0～5 m、5～10 m、10～15 m、15～20 m和20～25 m 5段，并计算各段的RMSE与MAE，结果如表5所示。

表5 分段统计Tab. 5 Segment statistics m

由表5可得，对于不同水深区间，改进后的模型精度优于传统BP神经网络模型，对不同的水深具有一定的适应性。相比于传统BP神经网络模型，在0～5 m、5～10 m、10～15 m、15～20 m和20～25 m水深段，改进后的算法RMSE分别减小了0.075、0.102、0.093、0.089和1.035 m，MAE减小了0.078、0.118、0.126、0.097和0.874 m。

利用改进前和改进后的神经网络模型分别对甘泉岛近岸全区域的水深进行了反演，结果如图8所示。

由图8可以看到，在甘泉岛上部珊瑚礁区域，传统模型的水深反演结果并未体现珊瑚礁之间较浅区域的地形纹理细节，而改进后的模型反演结果在此区域的一些细节表现较好。

图8 甘泉岛水深反演图Fig. 8 Water depth inversion diagram of Ganquan Island

3 结论

针对传统BP神经网络算法在水深反演中存在的权值更新模糊自适应问题，利用弹性梯度下降模型对传统算法进行了改进。实验结果表明：构建的算法能解决权值更新中参数过多、反演效率慢的问题，提高了水深反演的效率和精度；新的权值更新方法引出了“直接适应”的概念，只依据偏导数的符号进行学习和自适应，这使得算法能高效进行水深计算。由于加权步长的大小只取决于导数的符号，而不取决于导数的大小，使得学习速率在整个网络中平均分布，输入层的权重和输出层的权重获得同等增长，误差能更好收敛。弹性梯度下降模型可应用于水深反演，以甘泉岛作为研究区域，结合多光谱图像及多波束测深数据开展水深反演，采用本算法所反演水深的R2、RMSE、MAE和反演效率均优于传统算法，在不同水深段的表现优于传统的模型，且在0～15 m的水深反演结果RMSE小于1 m，表明本算法在15 m以下水深反演具有较高的适用性。