水轮发电机组导叶漏水量测量与评定

何东阳

(大唐水电科学技术研究院有限公司，四川 成都 610031)

水轮机导叶是水轮机引水发电系统的重要组成部分，机组通过调节活动导叶角度对工作流量进行调节，以实现运行工况的控制。理想状态下，机组处于停机态，水轮机导叶关闭后，机组流量应为零。实际上，由于导叶本身密封设计、制造，设备安装存在的瑕疵或缺陷，以及长期使用后形成的磨损或老化等情况，水轮机导叶通常存在一定程度的漏水现象。

作为一种常见现象，多数机组导叶漏水程度轻微，不易引起重视。但发展到一定程度一方面会造成水资源、水能资源浪费，给机组安全稳定运行带来不利影响，如造成机组停机困难[1]或者蠕动现象[2]，进而造成更严重的后果；同时，导叶的端面以及立面间隙过流时，流速的变化可能致使部分过流区域压力变化，若压力降至低于汽化压力，将导致空化和空蚀现象，进而损坏机组的过流部件。可见，水电机组的导叶漏水现象给水电站的经济运营和稳定运行带来了安全隐患，作为机组全生命周期的重要指标之一[3]，机组导叶漏水的状况应持续关注。

对于水电站导叶漏水量的测定及其计算，由于我国现行的标准、规程中未明确提出，因此长期以来没有指定或者比较通用的测量方法[4]。在开展相关工作时，应根据机组的情况、测试的条件以及测量设备，选取合适的测量、计算以及评定方法。目前，进行导叶漏水量试验常见的方法有通气孔法[5]、斜井法[3]、超声波法[6]以及节流孔板法[7]等，通常认为超声波法、节流孔板法的可靠度较好，但相关测量设备在水电站中并不常见，同时超声波法的设备在管道上部署时也有条件限制，普适性相对较差。而斜井法与通气孔法的原理相似，普适性较强，其中通气孔法通常认为在便捷性、可靠性上表现更好，在导叶漏水量测量时更为常见。

某电站1号混流式水轮发电机组额定出力为302.5 MW，工作水头范围在50～68.5 m，额定流量为580 m3/s。本文以该机组为例，采用通气孔法基本原理进行导叶漏水量的计算及评定研究。基本原理图见图1。

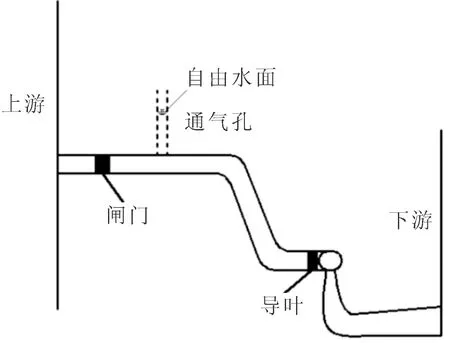
图1 基本原理图

1 测量方法及试验设备

某水电站进水口段由拦污栅、检修闸门、工作闸门、进水流道组成，通气孔位于工作闸门后斜井段。使用通气孔法测量时，确保机组处于停机态，进水闸门、导叶均关闭，并保证通气孔水面与上游水位基本持平。将工作闸门至导叶间流体看作整体，通气孔水面即其自由液面。由于导叶漏水，通气孔水面会持续降低，通过压力传感器持续测定导叶前后压力的变化，即可通过计算得到流体变化情况。

测量设备采用华科同安TTS332测试系统，由压力传感器、采集装置以及分析终端组成，采样率1 024 HZ，系统精度<1%FS，压力变送器精度等级为0.15级。

2 计算原理

导叶漏水量计算原理多采用容积法。关闭导叶及进水闸门，将上游流道内流体(即进水闸门至导叶前)视作一个整体如图1，该整体水量的变化速率为：

(1)

其中，F为自由液面处流道水平截面积，通气孔法测量时对应通气孔水平截面积。其水量的变化来自于进水闸门的漏水量Q2以及导叶漏水量Q，因此有：

Q=Q1+Q2

(2)

由于导叶后处于淹没状态，其间隙漏水为淹没出流，由伯努利方程易得到，导叶处出流流量与导叶前后自由液面高差H的关系可以表述为如下形式：

(3)

其中：α为流量系数，主要受出流间隙的尺寸影响；Q为导叶处出流流量，由此可见导叶前后自由液面高程差的开方与导叶处出流流量呈近似正比关系。

由式(1)～(3)，易推导得导叶前后压力水头随时间变化可表述如下形式：

H=att+bt+c

(4)

其中，a、b、c为常系数。

3 计算方法

3.1 最小二乘法二次曲线拟合法

由容积法的原理推导可知，可采用二次最小二乘拟合数学模型来描述导叶前后压力水头的下降过程，并可得到：

(5)

计算时，通过部署的压力传感器(从蜗壳、尾水处选取测点)，可测得导叶前后的连续压力变化值，计算得到导叶前后压力水头，将求得的压力水头与时间的关系进行二次最小二乘拟合，得到方程如式(4)，方程的各常系数代入式(5)即可得到Q1，结合测得的闸门漏水量，即可通过式(2)求得导叶漏水量。

由于最小二乘法二次曲线拟合法计算原理清晰、计算便捷、相对精确度较高，在测量导叶漏水量时，常常采用该方式进行计算。

3.2 斜率法

除了上述方法外，斜率法计算便捷，也有不错的适用性。受采集数据的影响，若采集的测点压力数据精度不够，采集的离散数据点形成的折线可能会呈显著的锯齿状，此时则不适合采用二次最小二乘拟合法进行分析，斜率法反而更为合适。该方法由于对数据精度以及采样率要求不高，即使水电站监测系统测点数据质量较低，也可以使用该方法进行计算。

采用斜率法进行计算时，根据导叶前后压力水头的变化趋势，选取工作闸门关闭后压力水头呈下降趋势的某一时刻t1，以及通气孔漏空之前压力水头下降趋势减缓前的某一时刻t2的测点数据，可得：

(6)

其中：P1、P2分别为t1、t2时刻的导叶前测点压力值；ρ为水的密度；g为重力加速度。为尽量消除数据精度的影响，减小误差，(t1-t2)段应根据趋势变化尽量取大。令(t2-t1)/2为t3时刻，Q2(t3)为该时刻的闸门漏水量，通过式(6)即可求得t3时刻的近似导叶漏水量，并由式(3)得到流量系数α，如下：

(7)

其中，P3、P4分别为t3时刻蜗壳及尾水的压力，得到流量系数α后，即可求得额定水头下对应的导叶漏水量。通常认为斜率法不够精确，但在压力传感器经检测在允许误差范围内，t1、t2时刻的选定符合导叶漏水趋势的情况下，一般认为可以作为导叶漏水程度判断的依据。

3.3 其他计算方法及实例计算结果对比

上述方法在试验时，还需测试闸门漏水量，测试时常采用容积法。确认进水闸门、导叶关闭，压力管道水体排空后，进入机组蜗壳处，可通过测量容器收集进水口漏水，并通过时间均值求得下泄流量，此外也可使用浮标法。由于通常情况下闸门漏水量较小，且测量不便，若无数据表征闸门存在水封损坏或其他原因导致的异常漏水情况，有时也做忽略处理[4]。

除了上述方法以外，利用容积法的基本原理，在测得的数据精度及采样率较好时，还可以使用切线斜率法计算导叶漏水量。该方法同样需要进行曲线拟合，其与二次最小二乘法曲线拟合的区别在于切线斜率法使用的曲线拟合方式非多项式拟合。计算时，先将采集的压力数值，处理及滤波后拟合得到平滑的导叶前后压力水头变化曲线。然后确定闸门完全关闭时刻，由式(3)可认为此刻导叶漏水量最大，也即导叶前后压力水头变化速率最大，因此由拟合得到的压力水头变化曲线切线斜率可确定闸门关闭的时间节点，同时由于闸门完全闭合时，前后平压，此时Q2=0。最后由式(1)即可得到理论闸门闭合时刻的导叶漏水量，并计算得到额定水头下的导叶漏水量。该种计算方法优势在于理论上可以近乎忽略闸门漏水对导叶漏水测量的影响，计算结果的精确度较高。

以某电站1号机组为例，采用通气孔法测量导叶漏水量。闸门关闭后至通气孔漏空前一段时间的采集的数据见表1。

表1 测量数据

利用采集的数据(单位kPa，数据精度为0.01 kPa)，采用最小二乘拟合方法计算，并忽略闸门漏水量，可得到拟合相关系数为0.999 8的二次曲线，并求得导叶漏水量为0.520 3 m3/s。同时，采用斜率法，分别使用原数据(数据精度为0.01 kPa)，以及做取整处理后数据(精确到kPa、10 kPa)进行计算，均忽略进口闸门漏水量，分别选取0～60、16～76、38～98 s三个时间段的数据开展计算，其计算结果见表2。

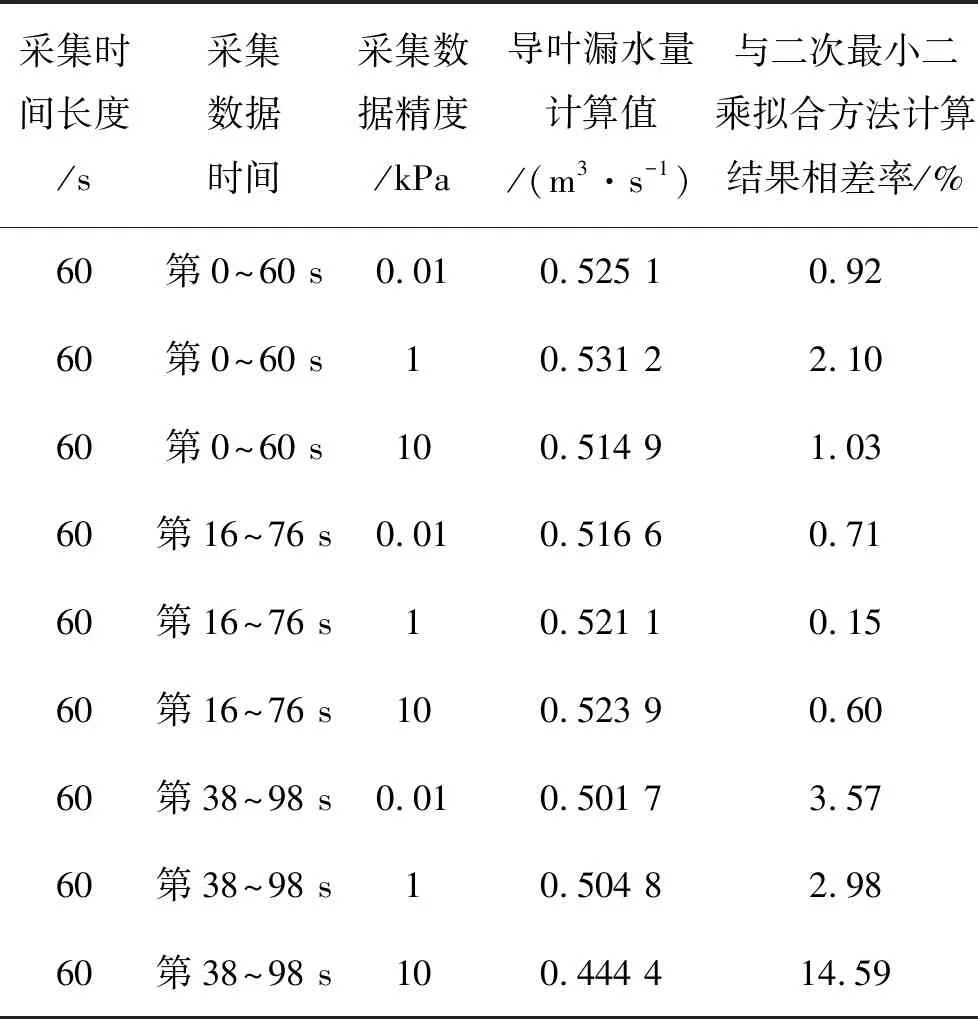
表2 斜率法计算结果

可见，采用斜率法计算，数据精度不足时，选取合适的时间段，对某电厂进行导叶漏水计算，其结果相对于最小二乘拟合方法的计算结果差别较小，其误差大小不影响对导叶漏水程度的判断。因此，在进行导叶漏水计算时，若条件有限，采用简单的斜率法计算也能保证结果的基本可靠性，可以以此来判断导叶漏水情况。该方法尽管准确度不如其他计算方法，但其简单易行以及对数据精度及采样频率要求低的特点，可供电厂运行人员对导叶漏水情况进行初步判定时使用。

4 评价指标

完成导叶漏水量的计算后，在对导叶漏水情况进行评价时，目前所能参考的指标较少。对于本文研究的圆柱式导叶的机组而言，国标[8]规定其导叶漏水量不应超过水轮机额定流量的0.3%。由式(3)可知，同一机组，其导叶漏水量应与导叶前后自由液面高程差的开方呈近似正比关系，流量系数α仅受导叶渗漏间隙的尺寸影响，该系数可以反映出导叶的实际密封能力。但流量系数α的大小无绝对值指标可以进行比较、分析；同时，不同机组的流量系数α也均不相同，因此，需要一个指标可以衡量、评价或比较任意机组的导叶密封情况，令：

(8)

其中：Q0为水轮机额定流量的0.3%～0.4%，由机组布置形式决定；α0为Q0在额定水头下的流量系数。由此可得到的无量纲导叶密封指标β，该参数可以直观的表示出水轮发电机组的导叶密封能力，也即反映出各机组导叶的漏水情况。β值越小，则导叶的密封性能就越好，导叶的漏水量也较低；反之则表明导叶的漏水问题更严重；当β>1时，导叶漏水量不符合国标要求，需要及时进行处理。

5 结 语

本文采用通气孔法的测量原理，对某电厂1号机组导叶漏水量进行测试。根据测量结果，分别分析、比较了最小二乘法二次曲线拟合法、斜率法、切线斜率法三种计算方法的优劣，并给出了通用性的评价指标。后续还会根据实际的运用情况，进行进一步的探讨。