电动自行车充电桩安装优化分配方法研究

杨玉林 肖磊 杨丽 李世隆 高党寻 秦海鹏

（1.江苏师范大学电气工程及自动化学院，江苏徐州 221116；2.中国自行车协会，北京 100079；3.清华大学基础工业训练中心，北京 100084）

为了充电安全，保证电动自行车不在室内充电，很多地方在室外安装了充电桩，但是在使用的过程中，出现了诸多问题，比如，部分充电桩使用率低，充电桩安装的数量过多或者过少，导致资源浪费或不足等。这些问题多是由充电桩安装初期评估不到位，安装位置和安装数量没有进行合理评价而导致的。因此，为了提高使用率，有必要针对电动自行车充电桩的安装进行优化分配，保证成本和用户满意度最大化。

用户的使用率最高，成本使用最低，以及用户满意度最大化，对上述三个指标求其最值，这本身就是一个优化问题，需要给出满足上述指标的最优方案。因此，建立上述问题的数学模型，然后基于该模型进行优化求解，从而给出一个较优的充电桩安装方案。

1 充电桩安装数学模型

为了获得充电桩安装的最优方案，首先需要对问题进行建模，也即，将上述三个指标采用数学公式表述出来。为了方便建模，以图1 的安装场景为例，假设充电桩的位置（取该充电桩的中心位置）为(xi,yi)，若有N 个充电桩，则所有N个的充电桩位置可以表示为Pos={(x1,y1),(x2,y2),…,(xN,yN)}，这N个充电桩的个数可以分别表示为Num={S1,S2,…,SN}，那么，本文需要解决的问题是，在已知环境周围有的充电桩信息，进一步安装新的充电桩，给出新的充电桩位置和数量，从而保证成本最低，利用率最高，从而保证用户满意度最大化。

图1 充电桩安装环境

1.1 充电桩数量确定

为了简化求解过程，首先确定充电桩的个数，然后进一步确定充电桩的位置。容易知道，充电桩的多少，和人流量以及电动自行车的数量有关，甚至和周围的岔路口的数量有关，更重要的是，还和周围充电桩的数量有关。基于此，本文考虑上述因素，构造关于充电桩数量的计算公式，具体如公式（1）所示。

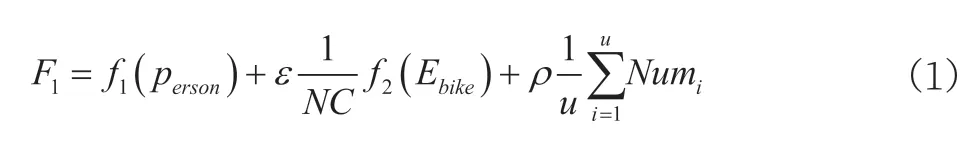
其中，f1(person)表示与人流量相关的函数，f2(Ebike)表示与电动车总数的函数，上述两项的计算则需要根据历史数据采用预测的方法来求取；第三项表示限定的周围环境中充电桩的平均个数；ε、ρ为一个[0,1]之间的参数，两个参数的值均需根据实际情况和经验确定；NC表示岔路口的个数。

充电桩的个数与安装成本成正比，因此，为了获取安装成本最低的方案，则需要求取F1的最小值。

1.2 充电桩位置的确定

为了求取满足上述三个指标的充电桩安装位置，设充电桩的安装位置为(x,y)，为了满足充电的利用率最高，则需要综合考虑周边所有充电桩的位置和数量，因此，本文中的充电桩利用率采用公式（2）来表示，具体如下：

其中，Num+1 表示限定区域中所有充电桩的个数，dj(x,y)表示需要安装的充电桩到第j个已安装充电桩的距离，j=1,2,…,Num。

充电桩的安装位置选定的主要因素是均衡化充电桩的利用率，从而避免利用率太低或者太高的情况，从而提高用户满意度，因此，本文中需要求取F2的最大值。

1.3 数学模型

考虑到上述两个因素，因此，构建本文所求问题的数学模型如公式（3）所示：

其中，第一个函数采用100 减去F1，其原因是一次充电桩安装的最大个数不会超过20 个，且上述操作是为了方便求取两个值的最大值。

2 求解方法

上述问题是一个多目标优化问题，本文采用加权的方式将其转化为一个单目标问题，如公式（4）所示：

其中，a与b为权重，且a+b=1。

针对上述问题也产生了许多求解方法，如穷举法、分支定界法，割平面法、启发式算法等。启发式算法目前是运用最为广泛的一类求解方法，这类算法虽然不一定能求到最优解，但可以在较短的时间内得到令人满意的次优解。因此，本文所求的模型，可以采用诸如微粒群优化算法（PSO）[1-2]、遗传算法（GA）[3]、蚁群算法（ACO）[4]、模拟退火算法（SA）[5]、自适应大规模邻域搜索算法（ALNS）[6]等方法来求解。其中较为常用的是PSO，GA 以及ALNS 算法。

微粒群优化算法是一种基于种群的随机优化技术，1995 年由R.C.Eberhart 和J.Kennedy 二人共同提出[7]。算法的灵感来源于一群觅食的飞鸟，所有飞鸟都不知道食物的具体位置，但是可以根据自己的判断获取和食物之间的距离。整个鸟群可以共享各自与食物之间的距离信息，从而向距离食物最近鸟的周边区域进行搜寻，最终找到食物。PSO 算法根据上述方式来寻找最优解，其计算流程如图2 所示。

图2 PSO 算法流程

遗传算法的原理是以一个种群中的所有个体为对象，每个个体之间的差异化主要体现在对应的染色体编码的不同。在产生了初始种群之后，根据适者生存，优胜劣汰的原则，种群会不断地演化繁衍并趋向于更优的解。该算法主要的步骤是：在每一代种群中，根据个体适应度大小选出相应的个体进行下一步操作。然后借助自然遗传学中的遗传算子进行交叉和变异，产生新的个体。适应度高的个体，对应更优的解。这个过程同种群自然进化一样，后代种群比前一代或几代种群适应环境的能力更强。因此，迭代结束后种群中的最优个体经过解码后，可以视作问题的最优解。GA 算法具体的算法步骤如图3 所示。

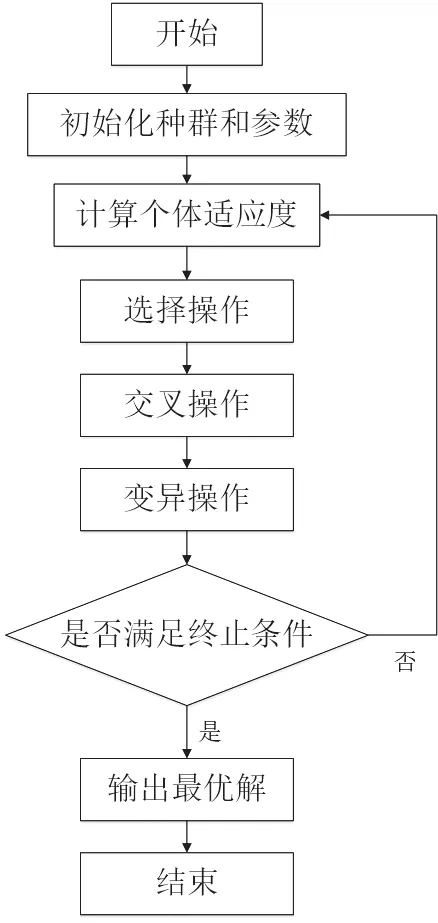
图3 GA 算法流程

ALNS 算法的实质是在每一次邻域搜索的时候都会变换邻域，从而增加搜索空间的广度。ALNS 算法将单一的移除和插入算子拓展成一组移除算子和一组插入算子集合。第一次迭代计算的时候，随机选择一个移除算子和插入算子来进行邻域搜索。在每一次的迭代计算结束后都会根据产生解的质量来给当前移除和插入算子进行评分。在随后的迭代计算中，移除和插入算子被选中的概率由其在之前的计算中累积的分数来决定。ALNS 算法会根据邻域解的优劣，自行调整邻域搜索操作。当获得了较优的邻域解后，算法会采取一定的策略接受该邻域解，如禁忌搜索接受准则[8]、模拟退火接受准则[9]、贪心接受准则[10]等。基本ALNS 算法的步骤如图4 所示。

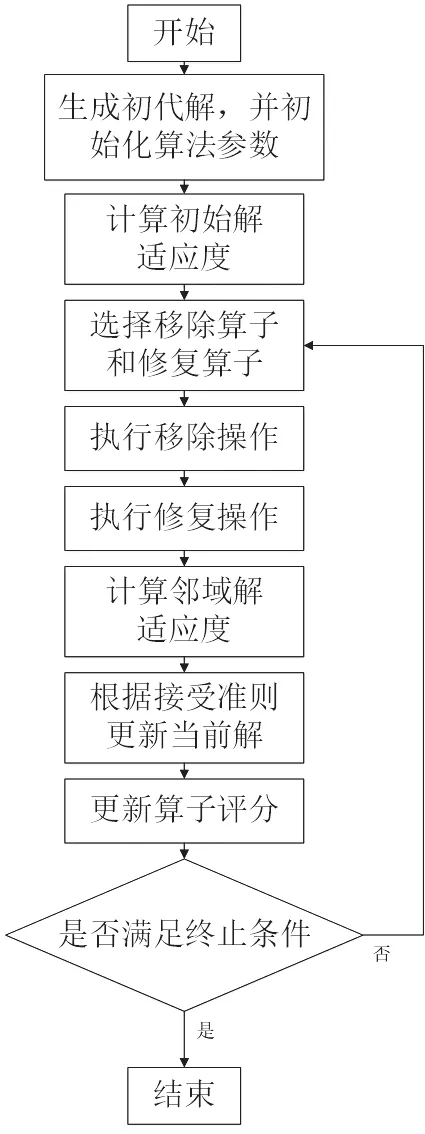
图4 ALNS 算法流程

采用上述三种方法，人为确定公式（4）中参数，则可以得到充电桩安装的数量和位置。

3 结束语

本文给出了电动自行车充电桩安装优化分配的数学模型，并给出三种方法来求解构建的数学模型。但是上述方法还存在需要改进的地方，比如，人流量和车流量的预测，需要根据大数据历史信息来进行预测，从而来保证模型的精确性；本文将双目标改成单目标，对权重的设置还需要人为来调参，有必要给出双目标求解方法，这些都是本文作者后期需要解决的问题。此外，将人工神经网络融入到本文问题的求解，也是一个需要考虑的研究方向。