基于SQKF的锂离子电池剩余寿命预测

2022-10-31黄梦涛胡礼芳张齐波

西安科技大学学报 2022年5期

黄梦涛，胡礼芳，张齐波

(西安科技大学电气与控制工程学院，陕西西安710054)

0 引言

近年来，新能源汽车凭借节能、低排放、经济等优势，迅速占据汽车市场。锂离子电池作为新能源汽车的主要动力源，随着充放电循环次数的增加，电池容量会不同程度的衰退，导致电池使用寿命缩短，电池性能退化。锂离子电池剩余寿命(remaining useful life，RUL)的精准预测，对于电池状态估计、预测性维护、自主健康管理具有重大意义，对保证新能源汽车安全稳定运行起到重要作用[1-3]。

目前，主流的锂离子电池RUL预测方法分为2类[4-5]。一类是基于数据驱动的预测方法[6-7]。使用锂离子电池全寿命周期的退化实验数据，利用机器学习算法运算，得出电池的退化状态。马里兰大学高级生命周期工程中心学者ZHANG等人使用弹性均方反向传播误差的方法自适应优化长短期记忆递归神经网络，并使用Dropout技术解决神经网络模型的过拟合问题。实验验证，该方法相对于传统的循环神经网络(recurrent neural network，RNN)可以更快速、更准确地预测出电池的RUL[8]。徐东辉等提出一种非线性组合预测模型，将Elman神经网络和非线性自回归神经网络(nonlinear auto-regressive model with exogenous inputs，NARX)预测得到的电池性能退化特征量，用最小二乘支持向量机和RBF神经网络进行非线性组合，预测电池的RUL。实验结果表明，2种方法的预测精度均比单一化的Elman神经网络和NARX神经网络精度高[9]。马里兰大学HU等将递归神经网络、支持向量机、相关向量机、贝叶斯线性回归模型等方法进行加权组合，发现加权组合的数据驱动方法预测精度高于单一的数据驱动预测方法的精度[10]。

另一类是基于机理模型的预测方法[11-12]。通过建立机理模型来表征锂离子电池的容量退化过程，再使用基于Bayesian估计的滤波方法精确估计电池的退化状态。同济大学DAI等在Thevenin模型上增加一个RC回路(极化电阻和极化电容并联组成一个RC回路)组成等效电路模型，在线辨识模型参数，完成RUL预测[13]。但在近似过程中，电池内部参量之间的一些重要隐含关系易被忽略，等效电路模型难以完全考虑复杂的外界条件，模型对电池的动、静态特性描述较弱。马里兰大学高级生命周期工程中心HE等使用大量退化实验数据，建立双指数经验容量衰退模型，使用粒子滤波算法辨识模型参数，并不断更新参数，实现RUL估计[14]。美国国家航空航天局艾姆斯研究中心的SAHA等通过电池的集中参数模型建立单指数经验容量衰退模型，使用粒子滤波算法有效地估计RUL[15]。

基于电池经验容量衰退模型的预测方法依据动力电池参数之间的关联性建立模型，模型的适用性强，易于获取。文中采用基于电池的经验容量衰退模型的方法预测锂离子电池的RUL，并设计平方根求积分卡尔曼滤波(square-root quadrature kalman filtering，SQKF)算法求解模型。

1 锂离子电池经验容量衰退模型建立

美国国家航空航天局(NASA)的一些学者研究发现，锂离子电池的电荷转移电阻与电解质电阻之和与容量C具有线性关系。SAHA等据此提出一个能反映电池容量衰退过程的电池机理模型[15]。模型考虑库伦效率对电池衰退的影响，也考虑电池静置引起的容量再生，模型见式(1)。

Ck=ηCk-1+β1exp(-β2/Δtk-1)

(1)

式中k为周期索引，代表第k次充放电周期；Ck表示第k个充放电周期的放电容量；η为库伦效率；Δtk-1为第k-1个充放电周期到第k个充放电周期的休息时间。β1和β2为待确定参数，受温度、电流倍率等因素影响，文中采用模型状态扩张的方法将未知参数辨识问题转为估计问题。为模拟外界干扰对模型的影响，引入系统误差和测量误差。采用如下方程描述β1,β2以及Ck的变化。

(2)

Zk=Ck+ψk

(3)

式中Zk为第k个周期的容量观测值；φ1,k-1，φ2,k-1，φk-1和ψk-1为彼此间相互独立的零均值高斯噪声。

令Xk=[x1,kx2,kx3,k]T=[β1,kβ2,kCk]T，ωk-1=[φ1,k-1φ2,k-1φk-1]，D=[001]，容量衰退模型状态方程

(4)

式中Xk为系统状态；Gk-1为噪声驱动矩阵，此处设为单位矩阵。Zk为状态观测矩阵；ωk-1和ψk-1为零均值高斯噪声，彼此独立，其协方差分别为Q和R。锂离子电池容量衰退模型的非线性传递函数

(5)

2 SQKF算法估计电池容量

2.1 SQKF

基于Bayesian估计的滤波方法中，求积分卡尔曼滤波(quadrature kalman filtering，QKF)算法[16]是应用Gauss-Hermite求积分准则选择采样点来近似函数的概率密度分布的非线性采样算法。其精度高于常用的扩展卡尔曼滤波(extended kalman filtering，EKF)[17]和无迹滤波(unscented filtering，UF)[18]，通过增加求积节点个数能继续提升精度[19]。

但在实际应用中，QKF容易受到数值误差的影响，导致非对称、非正定协方差的传播，使得滤波器发散。SQKF是QKF的平方根扩展，传递协方差矩阵的平方根，替换QKF的因式分解步骤，平方根的实现形式增强数值鲁棒性，确保状态协方差矩阵的半正定性，解决QKF的局限性。在一定条件下，SQKF的数值精度以及稳定性有很大提高[20]。

2.1.1 单变量Gauss求积节点及求积系数

SQKF的Gauss求积节点及求积系数与QKF算法一致。已知Gauss-Hermite求积公式[21-22]

(6)

式中xi和Ai分别为求积节点及对应系数；m为求积节点的个数。该积分公式有2m+1次代数精确度，可以看出，m越大，精度越高。该积分公式的权函数为ω(x)=e-x2，其m阶导数见式(7)。

(7)

(8)

求解式(7)中的零点，可以确定求积节点xi，求积系数通过公式(8)求解，并且均与函数g(x)无关。求积节点个数一般为3点求积分，5点求积分和7点求积分。为保证估计精度，文中选择7点求积分，求积节点和对应系数见表1[23]。

锂离子电池RUL估计问题是3维多变量问题，需要对单变量的求积节点进行多维扩展。

表1 Gauss求积节点以及求积系数

2.1.2 多变量Gauss求积节点及求积系数

张量积能够实现2个不同大小的矩阵的运算。设A的大小为m×n，B的大小为p×q，A与B的直积C=A⊗B,C的大小为mp×qn，张量积公式

(9)

x为服从高斯分布的三维变量，g(x)的期望

(10)

(11)

ξi={ξi1,…,ξim}T

(12)

式中I为n维单位矩阵；ωi由单变量求积系数的乘积组成；n为多变量的维数;ξi为由多个单变量求积节点构成的点向量；m为单变量时的求积节点数量，多维求积节点的总数量为mn。多维扩展的具体方法如下。

P1,∶=ξi,W1,∶=ωi

form=2∶dim(x)

A1∶m-1,∶=P⊗I1×n

Am,∶=I1×n⊗Pm-1,∶

B1∶m-1,∶=W⊗I1×n

Bm,∶=I1×n⊗Wm-1,∶

P=A

W=B

end

ξi=A∶,i

已知单变量求积节点与权值，P1,∶为求积节点的第一行，W1,∶为求积系数的第一行，⊗为张量积变换，求得多维变量的求积节点ξi和系数ωi。

2.2 SQKF跟踪估计锂离子电池容量

2.2.1 初始化状态变量及协方差

(13)

(14)

2.2.2 时间更新

用Cholesky分解法因式分解协方差矩阵Pk-1|k-1，得到下三角阵Sk-1|k-1

Sk-1|k-1=chol(Pk-1|k-1)

(15)

评估求积节点

(16)

非线性函数传递变换后的求积节点为

(17)

其中，f(·)为式(5)表示的非线性传递函数。

状态一步预测

(18)

(19)

(20)

式中 qr{·}表示QR分解。

2.2.3 量测更新

评估求积节点

(21)

评估非线性量测函数传递的求积节点

Zl,k|k-1=DXl,k|k-1,l=1,2,…,mn

(22)

估计预测的量测值

(23)

定义一个矩阵Zk|k-1来估计新息协方差矩阵平方根Szz,k|k-1

(24)

(25)

定义矩阵Γk|k-1来估计互协方差矩阵Pxz,k|k-1

(26)

Pxz,k|k-1=Γk|k-1Zk|k-1T

(27)

卡尔曼增益

Kk=(Pxz,k|k-1/(Sz,k|k-1)T)/Szz,k|k-1

(28)

估计更新的状态量

(29)

令U=KkSzz,k|k-1，得到状态估计协方差矩阵的平方根形式

Sk|k=cholupdate{Sk|k-1,U,-1}

(30)

2.3 SQKF估计锂离子电池容量的稳定性证明

SQKF估计电池容量的稳定性的证明分为2步：数值稳定性证明及收敛性证明。证明过程如下。

2.3.1 SQKF的数值稳定性证明

满足以下2个条件，则经由积分公式推导获得的滤波算法稳定。

1)求积节点集分布在积分区间内。

2)求积节点对应的权值都为正数。

SQKF的求积节点和系数通过Gauss-Hermite求积分准则获得。由表1可知求积系数均是正数，且求积节点全部位于积分区间。此外，引入了滤波算法的稳定因子I，规定算法稳定因子I越接近于1，稳定性越好。

(31)

式中ωl为求积系数，该式可以作为评判滤波算法稳定性的标准。可以证明，当ωl均为实数时，I恒大于等于1。当I>1时，即存在ωl为负数，对于有限字长精度运算的计算机，积分公式会引入大量的截断误差。SQKF的求积节点对应的权值均大于0，可得I恒等于1。即SQKF算法数值稳定。

2.3.2 SQKF的收敛性证明

北京航空航天大学的XIONG等认为算法的误差有界是采样型滤波算法收敛的充分条件[24]。

定义估计误差及预测误差

(32)

(33)

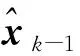
(34)

(35)

式中f′为非线性系统函数的一阶导数；f″为非线性系统函数的二阶导数;o(·)为高阶无穷小项。由式(32)～式(35)计算可知，预测误差exk|k-1

exk|k-1≈Fkexk-1

(36)

式中Fk为非奇异矩阵，可以表示为

(37)

式(37)对exk|k-1做一阶泰勒展开，可能引入状态误差预测的残差。为了得到一个精确的预测误差，引入对角矩阵Ak=diag(β1,k,β2,k,…,βl,k)，该对角矩阵与状态误差预测残差相关，故式(36)可以表示为

exk|k-1=AkFkexk-1

(38)

量测误差ezk|k-1定义见式(39)

(39)

由式(22)和式(35)可知，式(39)近似为

(40)

考虑量测误差残差的影响，引入一个与残差相关的未知对角矩阵Bk=diag(α1,k,α2,k,…,αl,k)，则式(40)可改进为

ezk|k-1=BkDexk|k-1

(41)

Fk为非奇异矩阵，若矩阵Ak满足下式

(42)

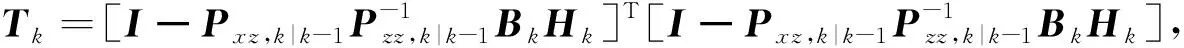
(43)

由式(42)可知，Ak的特征值越小，SQKF越容易收敛到0。但由于Ak和Bk是由人为假定的未知矩阵，可能使得式(43)不成立。此时，增加额外的正定矩阵即可使其成立。另外，Bk与系统的量测协方差噪声相关，协方差的噪声越小，Bk越接近单位矩阵，式(42)成立。

文中的经验容量衰退模型描述电池生命周期的容量变化，因此状态方程为有界函数。而电池容量的变化率也是一个有界函数。即预测误差exk|k-1

(44)

由式(43)和式(44)可得，SQKF的误差有界，SQKF估计电池容量具有收敛性。证明了SQKF估计锂离子电池容量的过程是稳定的。

3 仿真与验证

3.1 SQKF跟踪估计仿真

使用NASA卓越故障预测中心公开的锂离子电池数据集[25]进行RUL预测仿真实验，实验选用商用18650锂离子电池。

在相同的参数及初始值的情况下，对估计值采取蒙特卡洛求平均，蒙特卡洛次数设定为1 000次。过程噪声协方差Q=0.001×I3，量测噪声协方差R=0.001×I1。采用最优化方法确定初始值

(45)

(46)

SQKF对B5号锂离子电池容量跟踪结果如图1和图2所示，β1,β2估计结果如图3所示。

EKF，UF，QKF及SQKF等4种算法跟踪估计B5号电池容量的仿真实验误差见表2。由表2知，相同初值和噪声情况下，SQKF的估计误差均小于EKF，UF及QKF算法的估计误差。

表2 B5号电池容量的估计仿真实验误差

3.2 锂离子电池RUL预测仿真

将电池的前T个充放电循环的容量数据作为历史数据，使用4种算法跟踪估计。再从第T个周期迭代估计锂离子电池容量，每输出一个容量估计值，判断该估计值是否到达预先设定的阈值(文中设定阈值为电池容量的70%，即1.4 Ah)。若未到达失效阈值，则继续迭代估计；若到达失效阈值，则停止迭代，迭代的次数即电池剩余寿命。文中通过分析预测起始点的选取和电池个体差异对预测精度的影响，分析算法性能。

3.2.1 预测起始点对算法预测的影响

为分析验证预测起始点的选取对算法的影响，分别使用EKF，UF，QKF及SQKF算法对B6号电池做RUL预测仿真实验，起始点分别设为50，70和90，4种算法对B6号电池RUL预测的实验仿真如图4～图6所示。

图4～图6中，不同预测起始点情况下，4种算法对B6号电池的RUL预测仿真结果见表3。

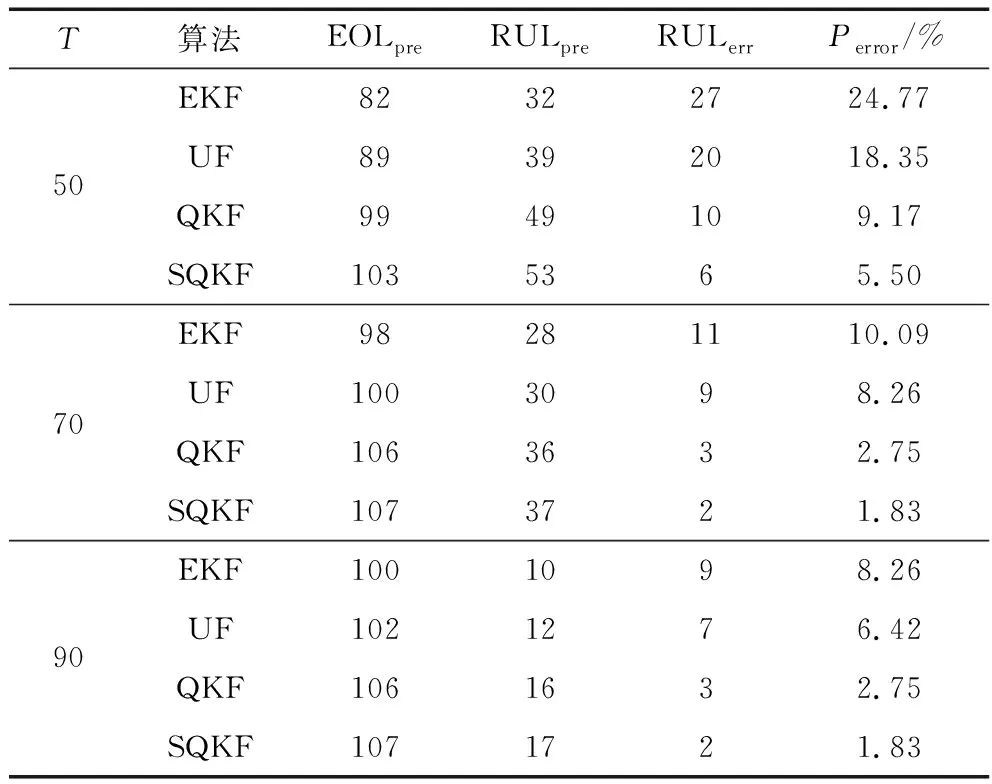
表3 不同预测起始点下B6号电池的RUL预测结果

表3中，实验从起始周期T开始预测，B6号电池的真实寿命结束周期EOL为109，RULtrue为RUL真实值，不同起始周期下RULtrue分别为59，39，19。EOLpre为各算法预测的寿命终止周期，RULpre为RUL预测值，RULerr为RUL预测的绝对误差，Perror为预测的误差率，定义如下所示。

RULerr=|RULpre-RULtrue|

(47)

(48)

由表3可知，一方面，在不同预测起始点下锂离子电池RUL的预测结果中，SQKF的精度总是高于QKF，UF和EKF，并且误差率总是保持在6%以内。另一方面，对于同一个电池(B6)，预测起点越大，容量的历史数据越多，预测就越准确。

3.2.2 电池个体差异对算法预测的影响

分析电池个体差异对算法预测的影响，起始周期T设为50，用4种算法分别对B6和B18号电池做RUL预测实验仿真。其中，B6号电池的RUL预测仿真结果如图4及见表3。B18号电池的RUL预测仿真结果如图7～图10所示。

B18号电池在起始周期T=50时，RULtrue=47，RUL预测仿真实验结果见表4。

结合表3～表4可知，一方面，SQKF的RUL预测误差小于EKF，UF和QKF，精度更高。另一方面，对于不同的单体电池，在相同的预测起始点下，EKF，UF和QKF的预测误差率均有所变化，但SQKF的预测误差率基本保持不变，说明SQKF预测算法的精度受电池个体差异影响较小。实验表明，SQKF方法在锂离子电池RUL预测中精度高、稳定性好，具有很好的应用价值。