基于AMSAA 模型的变环境车辆可靠性评估方法研究

徐泽宇，杨定富，周荣兴，孙宁，张营

（1.210037 南京市 江苏省 南京林业大学 汽车与交通工程学院；2.江苏省 南京市 32214 部队）

0 引言

车辆作为一种生产生活中的常用工具，其质量水平是人们关注的焦点。可靠性作为一个衡量产品质量水平的重要指标，正受到越来越多的关注。利用可靠性技术，可以发现排除产品的失效诱因，同时降低失效概率，进而提高产品的质量水准。车辆产品的质量竞争很大程度上就是车辆可靠性的竞争，因此生产者在设计制造的过程中必须高度重视产品的可靠性。

1 车辆可靠性评价方法概述

1.1 以往车辆可靠性评估方法

在以往的车辆可靠性研究中，以失效模式影响分析（FMEA）和故障数分析（FTA）2 种分析手段最为常见。FMEA 分析方法的优点在于，可以从部件、系统、整车3 个层面进行失效模式分析，但由于分析过程复杂，经验性评价参数较多，导致只适合于对车辆系统有高度理解的工程师团队使用，且整个过程以定性分析为主，无法准确评估试验过程中车辆可靠性水平的变化情况。FTA 分析方法的特点在于将车辆的各种失效机理转化成逻辑门线路的形式，可以在故障发生时利用计算机进行快速分析得到问题起因，而劣势在于在进行定量分析时，需要得出车辆各部件的失效概率，在车辆试制过程初期很难顺利得到足够量级的数据，从而导致无法得到准确失效概率[1]。为了实现整车可靠性水平的定量分析，需要引入其他可靠性分析方法。

1.2 AMSAA 模型的选用

根据以往机械研发经验可知，对于可修机械系统，其相邻故障间隔通常不属于独立同分布，而为了解决这一问题，可以使用非齐次泊松过程来分析处理这些既不互相独立也不满足相同分布的变量[2]。AMSAA（Army materiel system analysis activity）模型作为非齐次泊松过程模型的一种，常被用于描述复杂系统的可靠性分析与评估，并已经在机床、列车、航空设备等大型机械中得到了有效应用[3-5]。故本文以AMSAA 模型作为车辆可靠性分析的手段。

1.2.1 模型发展概述

20 世纪60 年代，美国通用电气公司的工程师 Duane 提出了最早的可靠性分析模型-Duane模型[6]，其特点为通俗易懂，便于制定可靠性计划。但由于只能实现参数的点估计，且评估误差较大，不利于精准分析。而后，美国陆军装备系统分析中心的 Crow 在Duane 的研究基础上提出了AMSAA 模型[7]，此模型考虑到机械系统故障的概率分布特征，使用非齐次泊松过程进行分析描述，大幅提高了对可靠性评价指标-平均故障间隔时间MTBF（Mean Time Between Failure）的估计精准性[8]。

1.2.2 模型使用方法

首先，在模型使用前为了确认是否适合用AMSAA 模型，需要对其进行拟合优度检验。利用式（1）可以计算得到拟合优度统计值CN2：

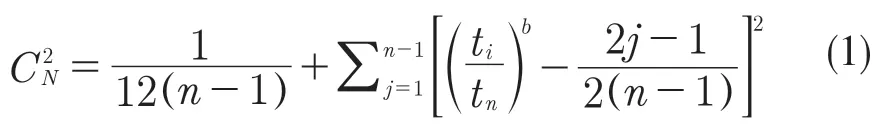
式中：n——试验期间故障总数；tn——最后一个故障的发生点；b——模型的形状参数（后文给出）。

之后，通过选定显著性水平α，根据Cramer Von Mises 检验表[9]查出与n、α相对应的拟合优度检验值CN,α2。如果统计值小于检验值，则说明当前数据是适合使用AMSAA 模型进行拟合分析的。

接着就对模型的特征参数进行计算。在计算形状参数b时存在两种情况（假设至少产生两次失效）

当故障数n＞2 时

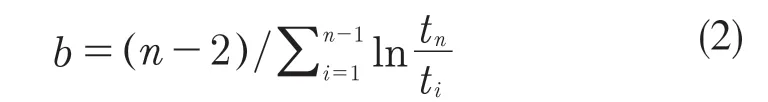
当故障数n=2 时

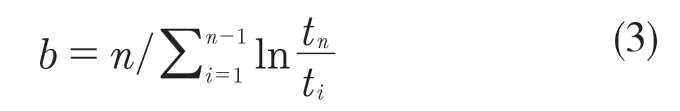
形状参数b的实际意义在于：当0＜b＜1 时，相邻失效的间隔增加，可靠性表现出增长趋势；当b＞1 时，相邻失效的间隔减小，可靠性呈现下降态势；当b=1 时，相邻失效的间隔退化为指数分布，可靠性保持不变[10]。

在求出形状参数b之后，便可得出对应的尺度参数a，以及可靠性评价参数MTBF：

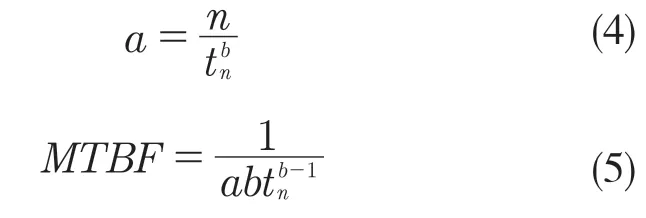
此外，由于多数可靠性试验的目的在于判断，经过一系列纠正措施产品的可靠性是否有了提升，这时就需要对试验数据进行增长趋势检验，主要步骤如下：

首先，根据式（6）计算出数据对应的趋势检验统计值X2

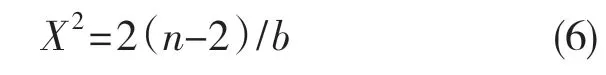
然后根据显著性水平α，利用X2分布求出检验值当统计值大于检验值时说明可靠性有增长趋势，有继续分析的意义。

1.2.3 模型预测功能

在完成模型相关检验和参数求解之后，可以利用已有数据对后续故障点进行预测。式（7）为在已知前n个故障数据的基础上，对第n+v次故障点的区间预测

当仅对下一次故障的发生点进行区间预测时，即v=1。令置信度γ=0.9，查阅资料[11]可得k1=0.105 6，k2=2.433 6，这样即可得到完整的故障点的预测公式。

2 模型在车辆可靠性评估中的应用

2.1 使用前需要处理的问题及解决方法

在以往使用AMSAA 模型进行可靠性分析的研究中，样品往往处于一个固定的试验环境下[5]，而车辆的使用情景是复杂的，这就意味着其可靠性试验的环境也必须是多样的，其中主要就包括高速环道、山区公路、越野路、石块路等等，这就导致了车辆的试验数据是一组多维的数据。在这种变化的试验环境下，车辆表现出来的使用性能和故障率往往有所不同，因而不能直接将多种环境下的数据直接代入到可靠性模型中。为了解决这个问题，需要将不同试验环境下的故障数据折算到一个统一的体系下，将多维数据整合成一维的数据，而这就引出了环境折合系数的这个概念[12]。其使用方法如下：

已知在车辆可靠性试验中共有m个(m≥2)试验路段，产品所经历的每个试验路段对应的环境折合系数为k1，k2，…，km。样品在试验期间发生的总故障数为n。产品发生第q次故障时，各试验路段的里程数分别为ttqi(i=1,2,…,m),所有故障数据构成一个n行m列的矩阵。

假设目前得到一组环境折合系数k1，k2，…，km，则可根据式（8）计算车辆在试验过程发生第q次故障时的折合试验里程，用tq表示（q=1，2，…，n）。

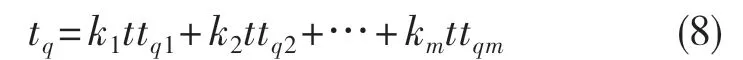
这样就使得故障数据从原来一个n*m的矩阵变成一个n*1 的向量，实现了数据整合的同时也降低了运算难度，为后续可靠性分析提供了帮助。

2.2 环境折合系数的求解方法

在明确了环境折合系数的作用之后，就需要对其进行相应的求解。在以往的研究中，常采用穷举搜索法，即根据工程经验来确定折合系数的寻优范围及相应的搜索步长，通过逐个计算进行对比筛选，最终得到一组合适的环境折合系数[13]。

而在本研究中，由于使用AMSAA 模型进行车辆可靠性研究的工程经验相对较少，难以得到可供参考的搜索范围和搜索步长，故只能在一个相对较大的范围内进行寻优求解，而这时使用穷举法求解会消耗大量时间和算力资源。为克服上述问题，现采用粒子群寻优算法PSO（Particle swarm optimization）来寻找折合系数。

粒子群算法的功能是在目标问题对应的多维空间中找到合适解。其实现过程主要如下：首先在解空间中设置指定数量的解粒子，并随机地给它们分配解空间位置和移动速度；然后计算各粒子的适应度，并根据解空间中所有粒子的全局最优点和各粒子的单体最优点依次更新各粒子的移动速度和空间位置。随着循环迭代的进行，寻优粒子将会聚集在一个或多个最优点周围，当达到迭代上限或者全局最优位置满足最小界限时，即可结束寻优过程。

2.3 环境折合系数求解过程

2.3.1 确定寻优约束和寻优目标

由于本研究是基于AMSAA 模型进行的，因而可以认为数据经过折算之后应该满足此模型的检验要求，故以拟合优度检验和趋势检验作为求解的约束条件。

在确定了约束条件之后，就需要寻找目标函数。由于拟合优度这个统计量涉及到了所有的环境系数，且在AMSAA 模型中拟合优度统计值越小说明数据与模型的契合度越高，故将拟合优度计算值最小化作为本次寻优的目标。

2.3.2 执行寻优操作

首先导入试验数据，选择种群规模和迭代次数上限并设置各路段折算系数范围；然后对各粒子在解空间的位置和速度进行初始化，进行迭代寻优直至找到目标解。由于粒子群算法作为一种仿生算法，其计算过程具有一定的随机性，故在求解折算系数时，可以多次执行寻优操作，记录每次寻优结果，在其中选择最符合实际意义的一组值留下，作为目标解。

3 实例分析与验证

对上文提出的可靠性评估方法进行验证，取2 辆试验车依次在高速环道、山区公路、凹凸不平路和越野路4 个路段的试验数据进行分析。

其中1 号车在高速环道774，3 200 km 处发生2 次故障；在山区公路6 018 km 处发生1 次故障；在凹凸不平路169，413，1 322，3 783，5 079，5 749，7 000，7 742，9 520 km 处发生10次故障；在越野路801，2 145，2 680，2 763，3 733，4 855，5 128，5 703 km 处发生8 次故障，共计20 次故障。2 号车在高速环道6 045 km 处发生1 次故障；在山区公路953 km 处发生1 次故障；在凹凸不平路7 167，9 972 km 处发生2次故障；在越野路1 811，2 539，3 210，4 203，5 075，5 878 km 处发生6 次故障，共计10 次故障。

在对各路段环境系数进行求解时，考虑到现实意义和寻优效率，需要先确认各路段系数间的相对关系。参考相似项目的研究结果[14]可以发现，当某一试验环节的故障频率有显著增长时，其对应的折算系数也会相应增大。而观察两辆试验车的故障情况，可以发现在凹凸不平路和越野路的故障频率要明显高于高速环道和山路，此时可以认定试验后两个路段的系数相对于前两个路段要更大一些，这也与越野路、凹凸不平路建设水平低、行驶难度高的实际情况相符合。

现将各路段的寻优范围定位为高速环路（0，10），山区公路（0，10），凹凸不平路（0，30），越野路（0，30）。以2 辆试验车的故障数据为基础，采用穷举法和PSO 算法进行寻优并进行对比，结果如表1 所示（为体现对比效果同时节约计算时间，使用穷举法时，k1k2的寻优步长设置为0.1，k3k4的寻优步长设置为1）。

表1 两种寻优方法的比较Tab.1 Comparison of two optimization methods

可以看到，粒子群算法消耗的时间要明显小于穷举法，其寻优目标值表现也更为优异。尽管穷举法可以通过缩小步长来进一步得到更好的目标函数值，但其花费的时间也会大大增长，降低了使用的方便性，并且从表中可以发现高速环路的系数要大于凹凸不平路的系数，体现出的物理意义为前者的使用环境与后者相对甚至要更加恶劣，但根据实际情况可知，凹凸不平路的行驶条件要更差，这就形成了矛盾。

在使用粒子群算法时，虽然单次得出的结果可能不是全局最优解，但其对目标值的搜寻表现尚可，且由于每次寻优时间较短，可以多进行几次寻优指令，在多个寻优结果中进行挑选，这样可以做到追求目标函数最优化的同时兼顾各系数间大小关系的合理化。

因此，选择粒子群算法的结果k1=0.3、k2=0.9、k3=4.7、k4=23.3 作为最后的折算系数取值。之后，即可利用模型对可靠性进行评估。

首先进行拟合优度检验，令置信度为0.9，查表得到两车检验值分别为0.172 和0.167,计算得到两车的拟合优度检验值分别为0.037 4 和0.098，均小于检验值，满足拟合优度检验。之后，进行趋势检验。令置信度为0.9，得到两车的趋势检验值分别为49.51 和25.98，而计算得到两车的趋势统计值分别为71.36 和27.43，均大于检验值，满足趋势检验。接着可得到两车在标准环境下MTBF 的点估计值分别为18 556 和33 948。为方便观察，现将其转化至最后的试验路段(越野路)上，其数值是796.39 和1 457。

通过观察故障数据可以发现两车的故障数成两倍关系，而在MTBF 最后的估计值上也体现出相似的关系，这可以反应出本模型的有效性和合理性。

此外，根据已有故障数据可对车辆故障点进行预测。为充分考量试验过程中纠正措施对整体可靠性增长的帮助作用，现取两车试验后期越野路上的故障点进行预测，并根据真实数据判断准确性，结果如表2 所示。为方便观察，已折算至越野路段。

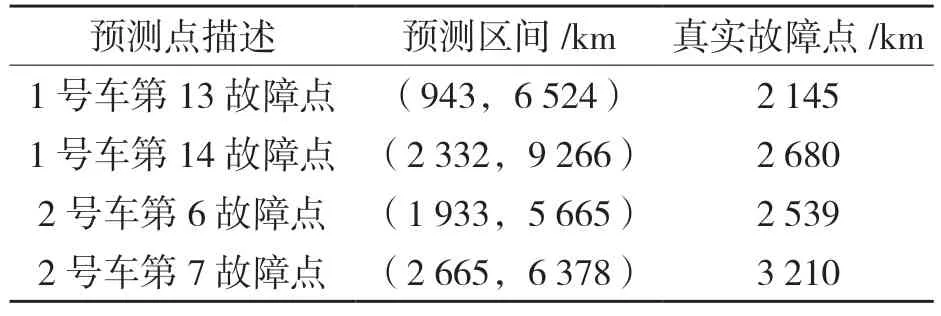
表2 基于AMSAA 模型的故障点区间预测Tab.2 Fault point interval prediction based on AMSAA model

由表可知，两辆车的真实故障点均落在了对应的预测区间之中，从侧面说明本文使用的折算系数求解方法的合理性。

4 结论

本文分析比较了以往车辆可靠性分析手段的优势与劣势，然后根据可靠性分析的进一步需求选取了便于定量计算的AMSAA 模型进行相关分析评价。在模型运用过程中，为了解决变环境下各试验路段数据统一的问题，使用了环境折合系数这一手段。而在求解不同路段对应的折合系数时，采用粒子群算法代替传统的定步长穷举法，解决了在缺乏历史经验的情况下，因寻优范围过大导致求解效率低下的问题，最终科学合理地求解了MTBF 这一可靠性评估的重要指标，且计算结果与试验数据表现出高度的关联性。此外，基于已有数据使用故障点预测公式进行了故障区间预测，发现预测结果准确有效。通过上述一系列的实例验证，表明本文使用的车辆可靠性评估方法符合工程实际，具有实用价值。