钢弹簧浮置板轨道条件下的轮轨接触特性分析

郭浩，朱祖男

（1.200093 上海市 上海理工大学 机械工程学院；2.201814 上海市 申通南车(上海)轨道交通车辆维修有限公司）

0 引言

轮轨接触分析在国内外已有多年研究。HERTZ 在研究中设定接触表面光滑无摩擦，所以2个接触物体之间没有摩擦力作用，只有法向力[1]。HERTZ 认为2 个弹性体在接触过程中产生的变形对其主曲率半径无影响。HERTZ 理论只能得到轮轨的法向力，但因为HERTZ 理论简单易用的特点，仍有学者和工程人员利用其分析轮轨接触问题[2]。CARTER 使用两圆柱体之间的滚动接触来模拟轮轨之间的滚动接触[3]。CARTER 模型只能用来研究二维的滚动接触，没有考虑自旋蠕滑行为，但其对于切向应力求解有很大的推动，且十分适用于分析轮轨滚动接触问题[4]。JOHNSON[5]在CARTER 建立的理论基础上，将圆柱体换成弹性球使得理论推广到了三维，并分析了流动方向和横向力对滚动的影响。这种方法简单直观，能获得确定的解析解，常应用于车辆动力学分析中，但V-J 理论未考虑自旋效应，V-J 对黏滑区的划分上存在错误。KALKER[6]在分析三维滚动接触问题时引入了蠕滑率，研究了蠕滑率对蠕滑力的影响。KALKER 线性蠕滑理论模型适合研究小蠕滑和小自旋情形的滚动问题[7]。几年后，KALKER 提出了简化理论，即假设接触区某一点的位移只与该点同方向的受力有关系。KALKER 采用HERTZ 的理论来研究法向接触的问题，还基于此模型开发了FASTSIM 程序来计算蠕滑和自旋所对应的蠕滑力，深受车辆动力学研究人员欢迎[8]。

浮置轨道有着较好的减震效果[9]，因此在地铁系统上被大量使用。在对其进行的相关研究中，耿传智[10]研究了加密弹簧支座、弹性支撑块对弹簧浮置版轨道的影响；姚纯洁[11]研究了弹簧支座间距、刚度以及扣件刚度对浮置板下沉量、应力与弯矩的影响。发现支座间距增大，下沉量、应力和弯矩的最大值都会随之增大，扣件刚度对浮置板下沉量最大值影响较小。

本文利用ABAQUS 建立钢弹簧浮置板，用Simpack 建立车辆模型分析了均速行驶的列车在钢弹簧浮置轨道条件下的轮轨法向力、横向力以及脱轨系数的情况。

1 车辆-钢弹簧浮置轨道模型的建立

1.1 钢弹簧浮置轨道模型

先利用ABAQUS 建立钢弹簧浮置板模型，再将其导入Simpack 中与钢轨进行耦合。每块钢弹簧浮置板长3.576 m，宽2.7 m，厚0.37 m。杨氏模量为3.5e10，泊松比为0.2，密度2 500 kg/m3。每块板沿车辆行驶方向扣件和弹簧均为6 组，扣件连接点距线路中心线为0.753 m，钢弹簧连接点距线路中心线为0.9 m，板缝为0.024 m。钢轨长21 m，杨氏模量2.06e11，泊松比为0.3，密度为7 850 kg/m3。建立的钢弹簧浮置轨道模型如图1 所示。

图1 钢弹簧浮置轨道模型Fig.1 Model of steel spring floating track

1.2 车辆模型

本文以上海地铁16 号线16A02 型电动列车为研究对象。用Simpack 建立其车辆模型前需确定其对应的拓扑结构，拓扑结构会影响结果的准确，过于复杂也会导致计算效率降低和求解时间明显增加。本文建立的拓扑结果如图2 所示，电动列车部分参数如表1 所示。

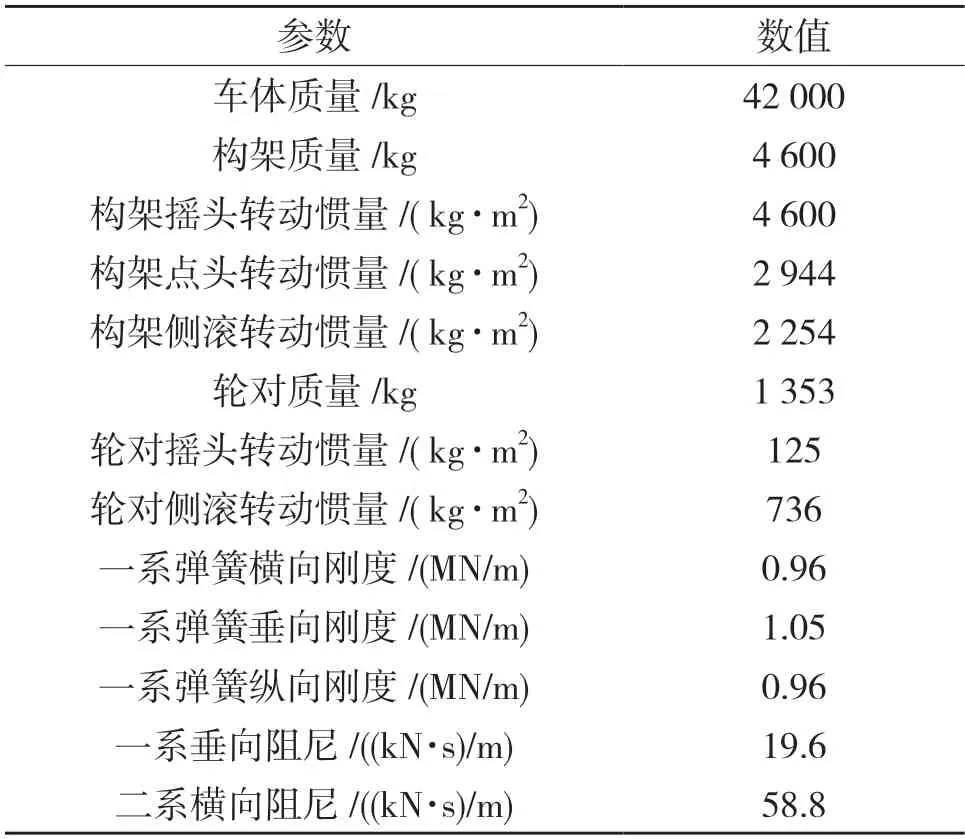
表1 16A02 型电动列车部分参数Tab.1 Some parameters of 16A02 electric train

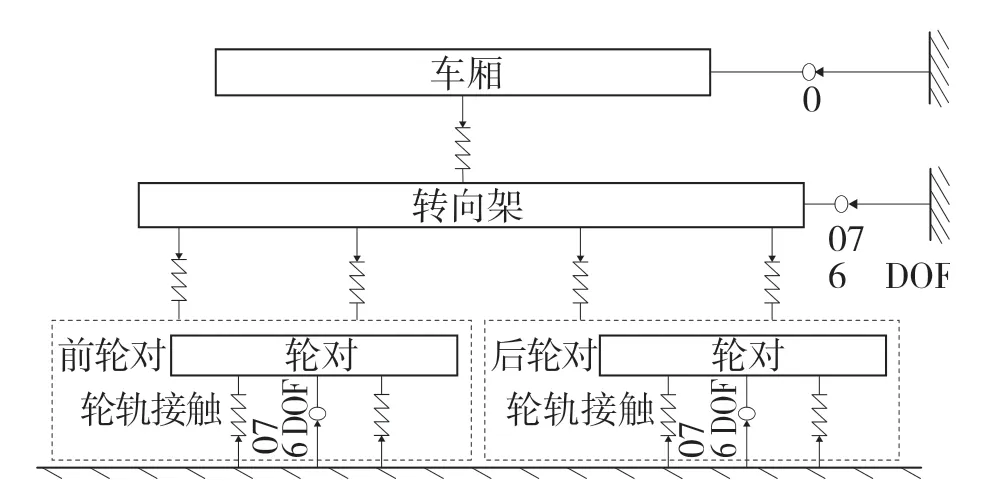
图2 列车拓扑结构图Fig.2 Train topology diagram

由于我国轨道不平顺性与美国五级轨道谱（PSD）相近[12]，因此本文使用此五级谱来模拟轨道的不平顺性，表达式如下：

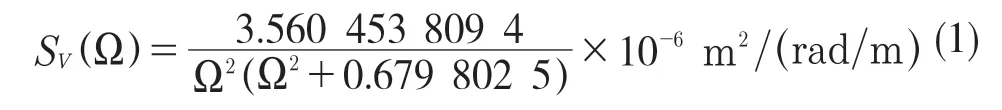
式中：SV(Ω) ——功率谱密度；Ω——空间频率。

根据列车拓扑图与车辆参数建立的列车模型如图3 所示。

图3 车辆模型Fig.3 Vehicle model

2 仿真结果与分析

地铁车辆通常平均时速为60 km/h，因此本文分析列车以60 km/h 通过钢弹簧浮置板轨道时轮轨垂向力、横向力和脱轨系数的相关情况。为方便说明，图4 展示了各车轮的编号，例如标号1 表示列车车厢前转向架第1 个轮对的左车轮。图5、图6展示了列车各个车轮受到的轮轨垂向力Q 的情况。

图4 列车车轮编号示意图Fig.4 Schematic diagram of train wheel number

如图5、图6 所示，同一轮对的左右车轮的轮轨接触垂向力基本相同，不同轮对之间的轮轨接触垂向力有较大区别，在浮置轨道上行驶时，轮对1上最大垂向力为81 132.7 N，轮对2 上最大垂向力为81 490.4 N，轮对3 上最大垂向力为83 318.3 N，轮对4 上最大垂向力81 542 N。最大轮轨垂向力在车轮6，即后转向架前轮对的右车轮。

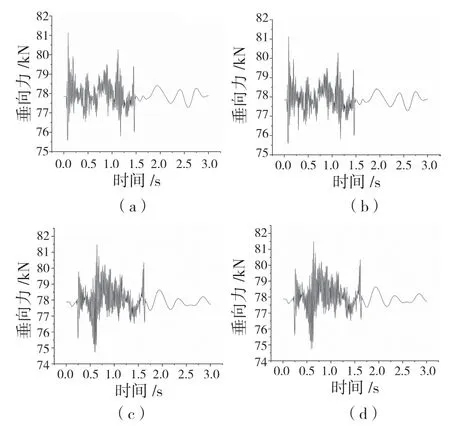
图5 转向架1 各轮垂向力Fig.5 Vertical force of each wheel of bogie 1

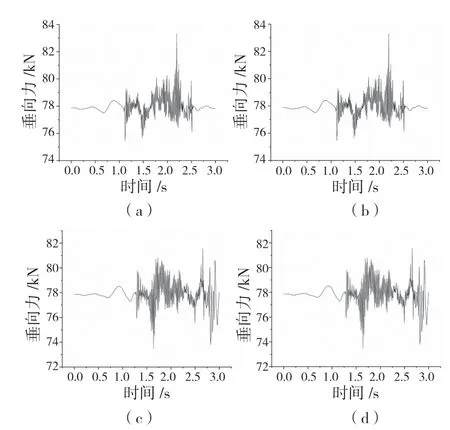
图6 转向架2 各车轮垂向力Fig.6 Vertical force of each wheel of bogie 2

表2 展示了车辆各个车轮位置的最大的轮轨接触横向力以及最大脱轨系数，如表2 所示。最大的轮轨接触横向力为806.6 N，最大的脱轨系数为0.100 57，与垂向力一样出现在车轮6。在国标规范中脱轨系数评定限值≤0.8，可见仿真结果在安全范围内。

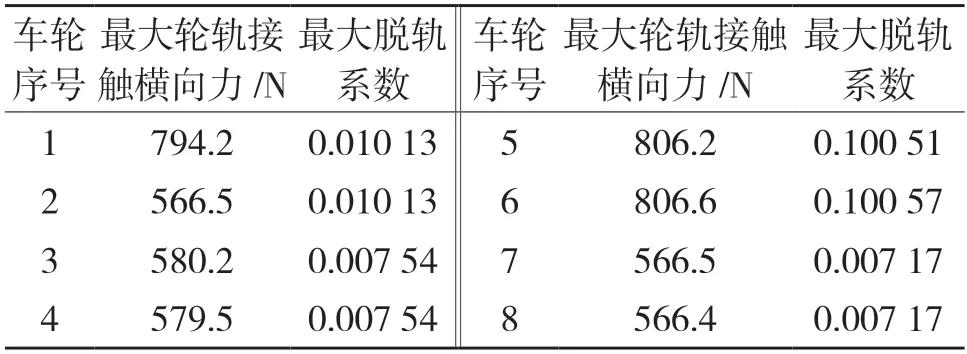
表2 列车车轮最大横向力和脱轨系数Tab.2 Maximum lateral forces and derailment coefficients of train wheel

3 结论

本文以上海地铁16 号线为车辆模型，建立钢弹簧浮置轨道模型，分析了列车行驶过程中的垂向力、横向力和脱轨系数的变化情况。在均速60 km/h 的情况下，列车同一轮对垂向力有着相同的变化趋势。最大垂向力为83 318.3 N，最大横向力为806.6 N，最大脱轨系数为0.100 57，并且三者的最大数值都发生在车轮6 上，即后转向架前轮对的右车轮。本文分析了钢弹簧浮置轨道条件下列车轮轨接触特性，为进一步分析列车的动力学特性以及车轮磨损作了铺垫。