CR-CR 型9 速自动变速器的杠杆法计算分析

宫涛，罗美琴，鲁庆东

（644003 四川省 宜宾市 宜宾职业技术学院 汽车与轨道交通学院）

0 引言

多挡化是汽车自动变速器的发展趋势[1]。多挡自动变速器多以拉维娜式、辛普森式及CR-CR 式行星齿轮机构为基础，增加1～2 排行星排构成[2]。其中CR-CR 型行星齿轮机构所用元件更少，结构紧凑，质量更轻，被越来越多的汽车厂家采用在9挡变速器中[3]，如奔驰9 速自动变速器[4]、采埃孚9 速自动变速器[5]、通用汽车9 速自动变速器[6]。

9 速自动变速器自由度多，传动比计算复杂，常用方法有传统的公式计算法、矩阵法、图论法、二次反转法、杠杆法[7]。杠杆法最直观，广泛运用于行星齿轮机构传动特性分析、计算验证和研究设计[8]，能反映自动变速器行星齿轮机构运动特性[9]。詹长书[10]等利用杠杆法研究了采埃孚公司的8 速自动变速器，建立各挡等效杠杆图，计算了各挡传动比公式；李明圣[11]等基于杠杆法对三排行星齿轮机构的混联方式的传动方案进行分析；侯国强[12]等运用瞬心-速度矢量法绘制了辛普森式行星齿轮变速器6 种传动方案的速度矢量图，根据相似三角形原理计算了其传动比并进行了验证。

传统杠杆法的应用为自动变速器的设计和研究提供了很好的参考，但是对于很多一线技术人员和初学者来说不够直观，理解有难度，尤其是CR-CR 型行星齿轮机构。CR-CR 型是双行星齿轮排机构，前排行星架与后排齿圈固定连接，前排齿圈与后排行星架固定连接。本文分析通用汽车GF9型 9 速自动变速器，提出一种基于杠杆法建立空间速度矢量图进行运动分析和传动比计算的方法，直观易懂。

1 GF9 自动变速器结构分析

GF9 自动变速器自2017 年3 月起装备在汽车上。它有3 组离合器、3 组制动器、1 组单项离合器、3 组串联式行星齿轮组，结构示意图如图1 所示。通过不同执行元件，产生9 个前进挡和1 个倒车挡，各挡位执行元件工作情况如表1 所示。

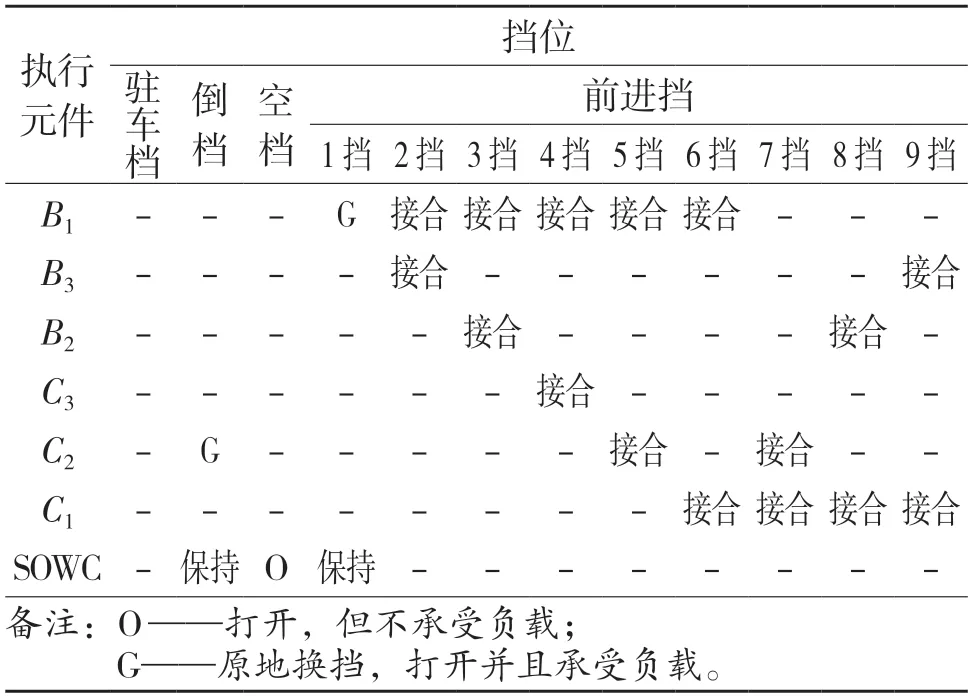
表1 各挡位执行元件工作表Tab.1 Worksheet of each gear actuator

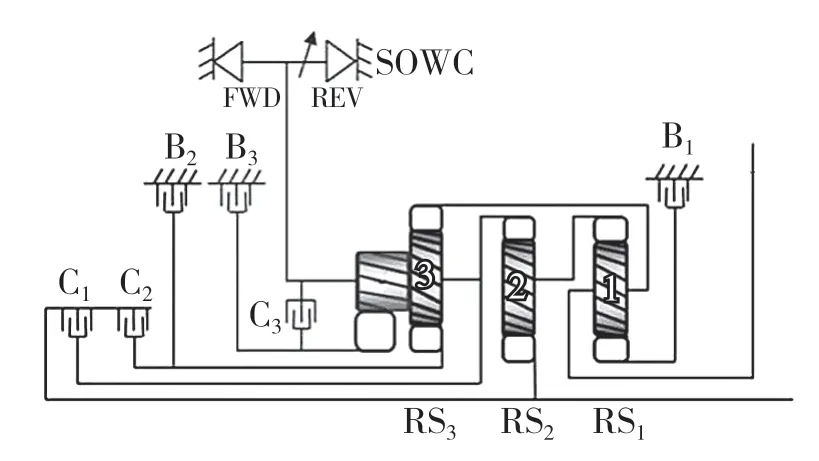
图1 GF9 自动变速器结构示意图Fig.1 Schematic diagram of GF9 automatic transmission structure

2 杠杆法原理

杠杆法可对等效后的杠杆进行运动学和动力学定性分析[13]。9 挡自动变速器的行星齿轮装置由3 组行星齿轮排组构成，可以分解成4 个单排行星齿轮机构，如图2 所示。

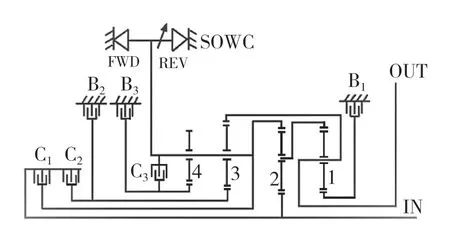
图2 GF9 自动变速器结构简化图Fig.2 Simplified structure of GF9 automatic transmission

采用等效杠杆法，将图2 中4 个行星齿轮排进行等效简化，如图3 所示，3 个支点分别表示太阳轮Si、行星架Pi和齿圈Ri。其中，Si表示行星齿轮排i 的太阳轮；Pi表示行星齿轮排i 的行星架；Ri表示行星齿轮排i 的齿圈。设PiRi=Ki，则SiPi=Kiαi，αi为行星齿轮排i 的齿圈齿数与太阳轮齿数之比，i=1，2，3，4。

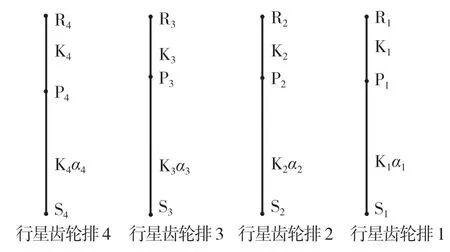
图3 4 个行星齿轮排等效杠杆图Fig.3 Equivalent lever diagram of 4 planetary gears

根据行星齿轮机构连接关系，将其进行简化，简化后的各行星齿轮排处于同一平面。由于行星齿轮排3 和4 均为反作用行星齿轮排，在不同挡位时工作。为了便于研究，特将机构简化为2 个平面，如图4 所示。

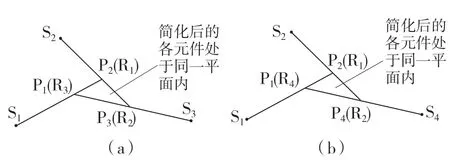
图4 GF9 自动变速器行星齿轮机构简化平面Fig.4 Simplified plane of planetary gear mechanism of GF9 automatic transmission

在行星齿轮排简化平面上，构建垂直于平面的速度矢量，规定向上的方向为正向，便可以根据杠杆的基本关系对各支点的运动和受力进行分析。

3 各挡传动比杠杆法计算

3.1 D 位1 挡传递路线分析和传动比计算

D 位1 挡时，换挡执行元件B1 和SOWC（单向锁止）工作，参与工作的行星齿轮排为行星齿轮排1 和行星齿轮排2，动力传递路线为：输入轴→S2→P2（R1）→P1→输出。构建D 位1 挡速度矢量图如图5 所示。

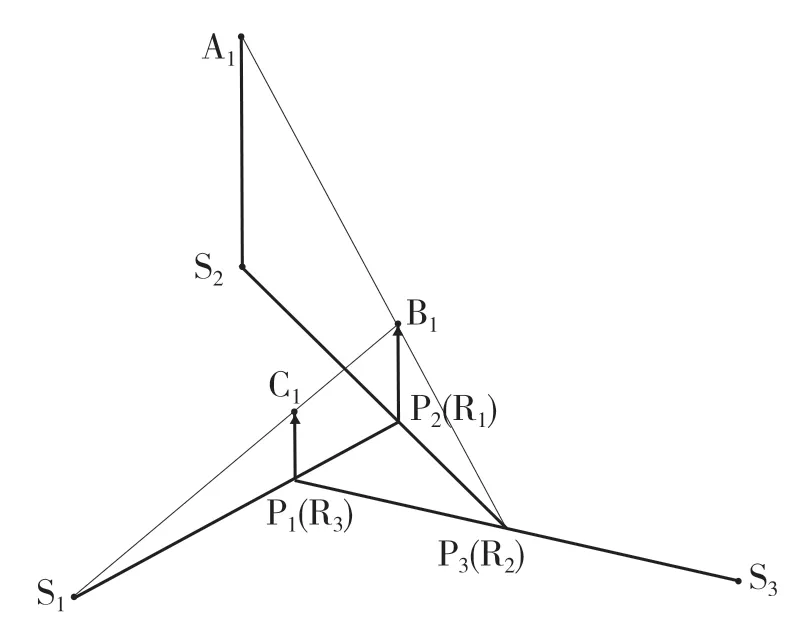
图5 D 位1 挡速度矢量图Fig.5 D position 1st gear speed vector diagram

动力由S2输入，从P1（R3）输出，因此D 位1挡传动比

由相似三角形得

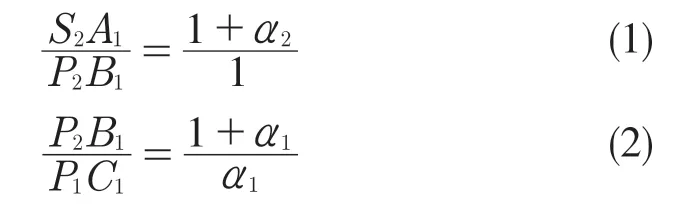
将式（1）、式（2）相乘得

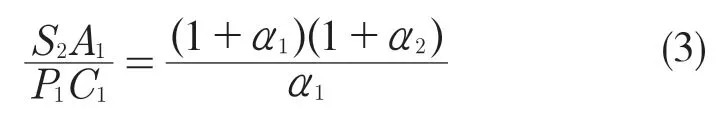
因此，D 位1 挡传动比为

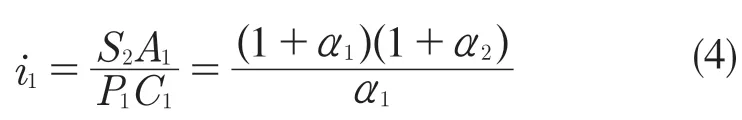
3.2 D 位2 挡传递路线分析和传动比计算

D 位2 挡时，参与工作的换挡执行元件有B1和B3，参与工作的行星齿轮排为行星齿轮排1、行星齿轮排2、行星齿轮排4，动力传递路线为输入轴→S2→P2（R1）→P1→输出。构建D 位2 挡速度矢量图如图6 所示。

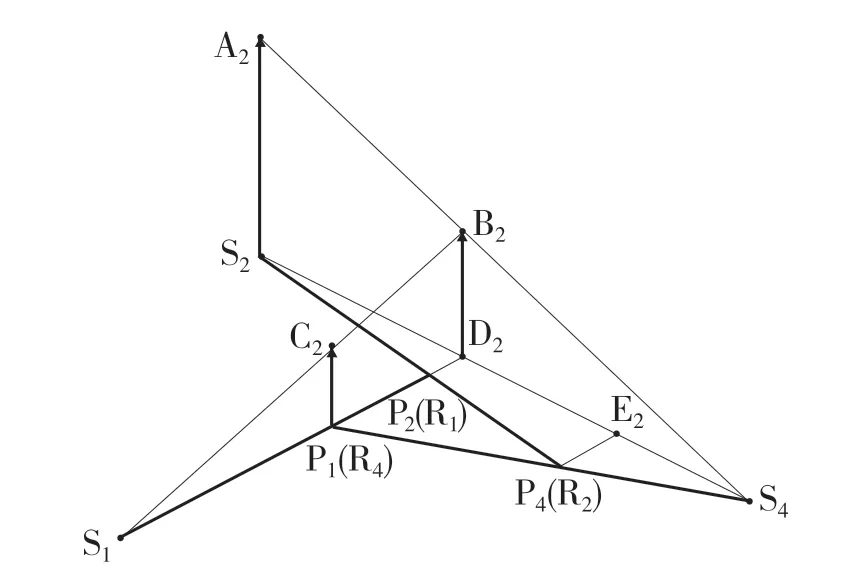
图6 D 位2 挡速度矢量图Fig.6 D position 2nd gear speed vector diagram

动力由S2输入，从P1（R4）输出，因此D 位2 挡传动比

假定S2D2的长度为a，D2E2的长度为b，E2S4长度为c，E2P4长度为d，D2P2长度为e。

由相似三角形得

式（7）、式（8）相乘得：

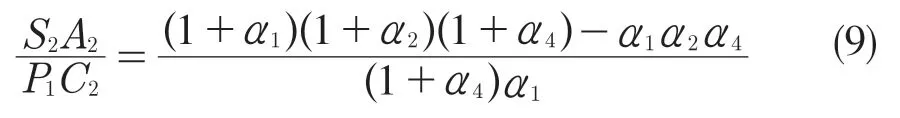
因此，D 位2 挡传动比为

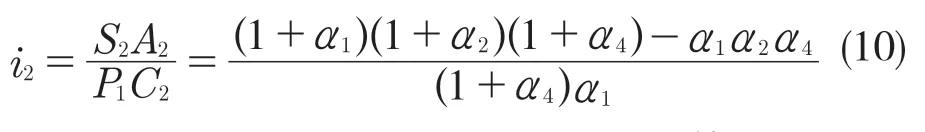
3.3 D 位3 挡传递路线分析和传动比计算

D 位3 挡时，参与工作的换挡执行元件有B1和B2，参与工作的行星齿轮排为行星齿轮排1、星齿轮排2 和星齿轮排3，动力传递路线为输入轴→S2→P2（R1）→P1→输出。构建D 位3 挡速度矢量图如图7 所示。

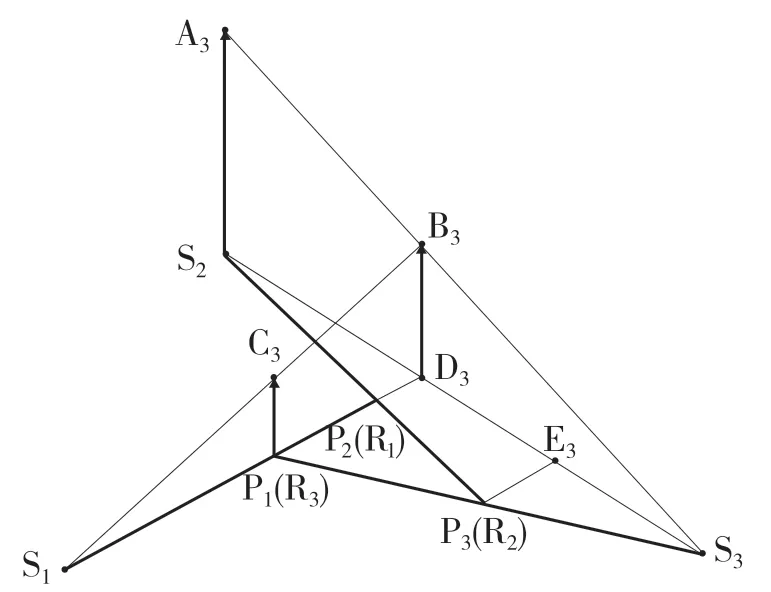
图7 D 位3 挡速度矢量图Fig.7 D position 3rd gear speed vector diagram

由公式（11）（12）相乘得

3.4 D 位4 挡传递路线分析和传动比计算

D 位4 挡时，参与工作的换挡执行元件有B1和C3，参与工作的行星齿轮排为行星齿轮排1、行星齿轮排2 和行星齿轮排4，动力传递路线为输入轴→S2→P2（R1）→P1→输出。构建D 位4 挡速度矢量图如图8 所示。

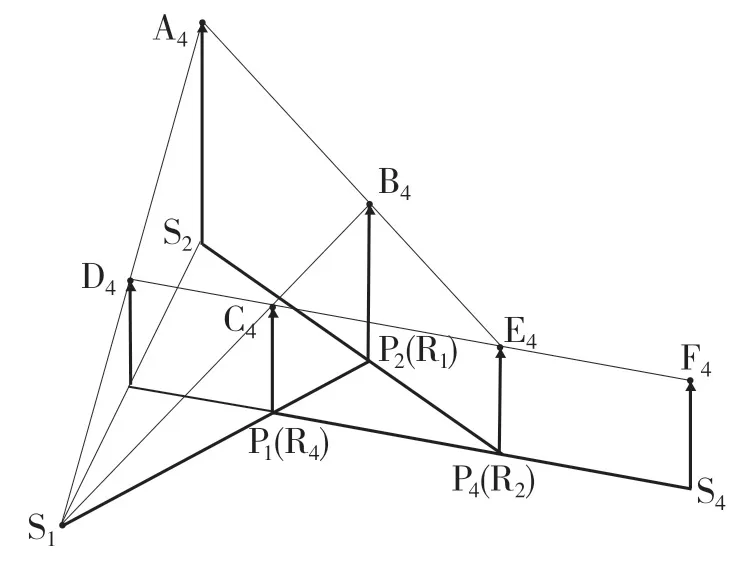
图8 D 位4 挡速度矢量图Fig.8 D position 4th gear speed vector diagram

动力由S2输入，从P1（R4）输出，因此D 位4 挡传动比

由相似三角形得：

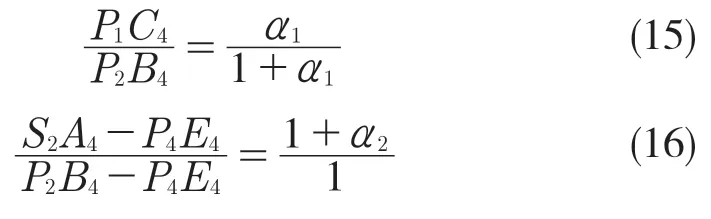
因为P1C4=P4E4，所以

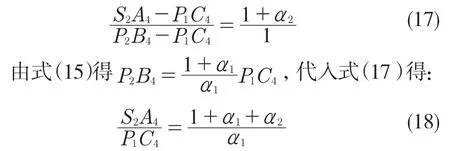
因此D 位4 挡传动比为

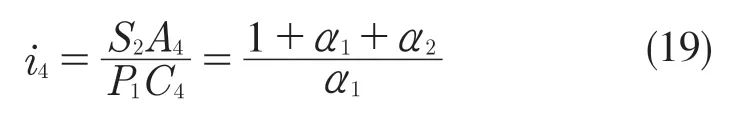
3.5 D 位5 挡传递路线分析和传动比计算

D 位5 挡时，参与工作的换挡执行元件有B1和C2，参与工作的行星齿轮排为行星齿轮排1、行星齿轮排2 和行星齿轮排3。动力传递路线分为2 路，第1 路为输入轴→S2→P2（R1）→P1→输出，第2 路为输入轴→S3→P3（R2）→P2（R1）→P1→输出。构建D 位5 挡速度矢量图如图9 所示。

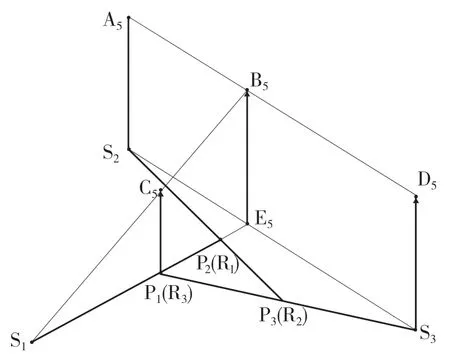
图9 D 位5 挡速度矢量图Fig.9 D position 5th gear speed vector diagram

因S2与S3速度相同，故S2A5=E5B5=S3D5，因此D 位5 挡传动比为：

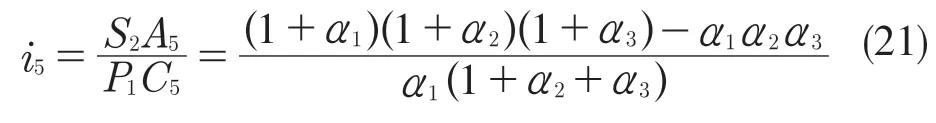
3.6 D 位6 挡传递路线分析和传动比计算

D 位6 挡时，参与工作的换挡执行元件有B1、C1，参与工作的行星齿轮排为行星齿轮排1 和行星齿轮排2。动力传递路线分2 路，第1 路为输入轴→S2→P2→R1→P1→输出，第2 路为输入轴→P3→R2→P2→R1→P1→输出。构建D 位6挡速度矢量图如图10 所示。

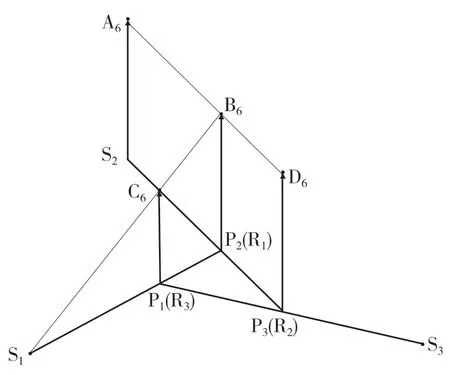
图10 D 位6 挡速度矢量图Fig.10 D position 6th gear speed vector diagram

动力由S2和P3输入，从P1（R3）输出，因此D 位6 挡传动比

由相似三角形得：

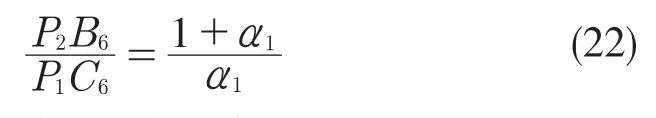
因S2与P3速度相同，故S2A6=P2B6=P3D6，因此D 位6 挡传动比为

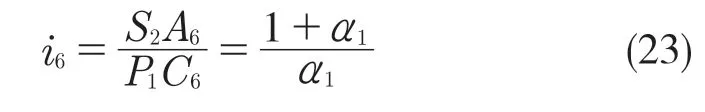
3.7 D 位7 挡传递路线分析和传动比计算

D 位7 挡时，参与工作的换挡执行元件为C2和C1，只有行星齿轮排3 参与工作。动力传递路线为输入轴→S3、P3→R3（P1）→输出。构建D位7 挡速度矢量图如图11 所示。

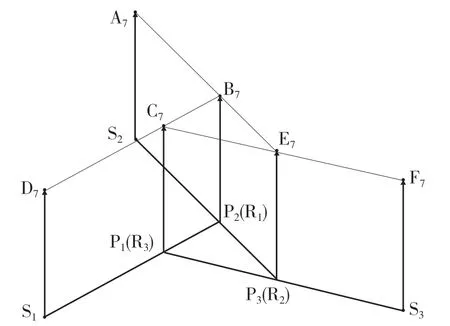
图11 D 位7 挡速度矢量图Fig.11 D position 7th gear speed vector diagram

图中，S3、P3同为输入，速度相同，根据行星齿轮运动特性得S3、P3、R3同速同向转动，D 位7挡传动比为

3.8 D 位8 挡传递路线分析和传动比计算

D 位8 挡时，参与工作的换挡执行元件有B2和C1，只有行星齿轮排3 参与工作。动力传递路线为输入轴→P3→R3（P1）→输出。构建D 位8 挡速度矢量图如图12 所示。

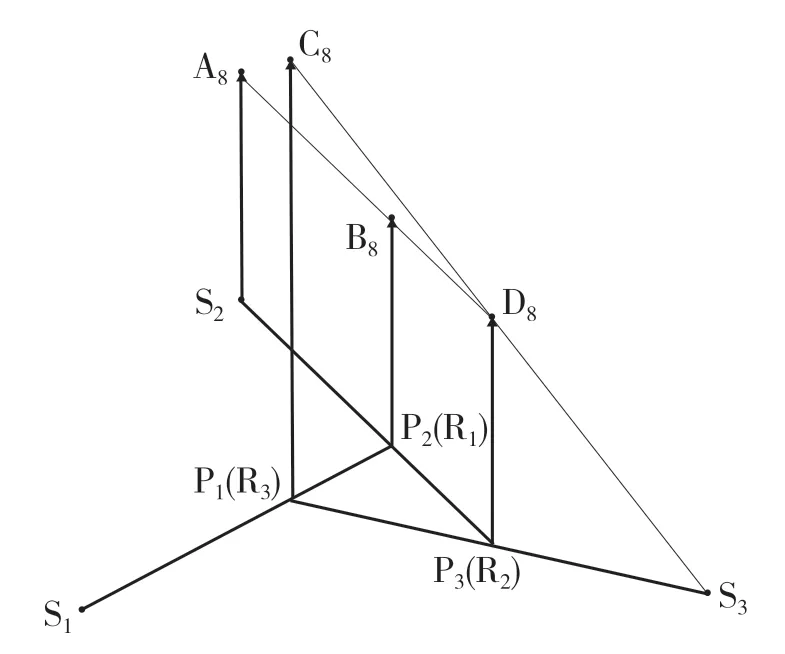
图12 D 位8 挡速度矢量图Fig.12 D position 8th gear speed vector diagram

动力由P3输入，从R3输出，因此D 位8 挡传动比

由相似三角形得

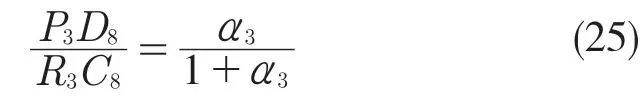
因此D 位8 挡传动比为

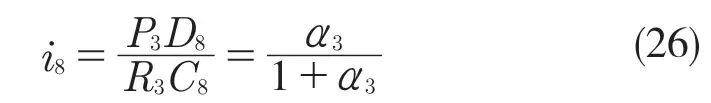
3.9 D 位9 挡传递路线分析和传动比计算

D 位9 挡时，参与工作的换挡执行元件有B3和C1，只有行星齿轮排4 参与工作。动力传递路线为输入轴→P4→R4（P1）→输出。构建D 位9 挡速度矢量图如图13 所示。

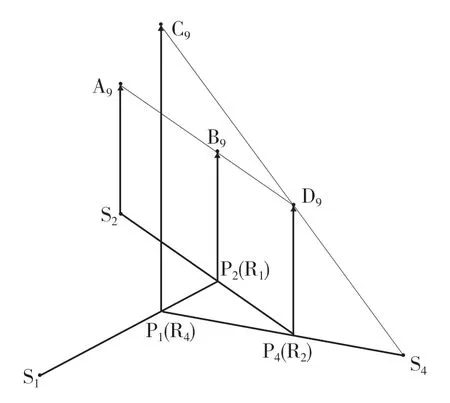
图13 D 位9 挡速度矢量图Fig.13 D position 9th gear speed vector diagram

动力由P4输入，从R4输出，因此D 位9 挡传动比

由相似三角形得

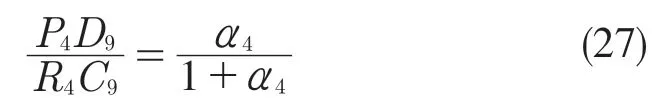
因此D 位9 挡传动比为

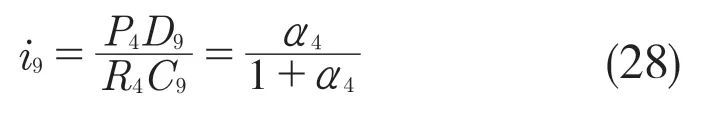
3.10 R 挡传递路线分析和传动比计算

R 挡时，参与工作的换挡执行元件有SOWC和C2，只有行星齿轮排3 参与工作。动力传递路线为输入轴→S3→R3（P1）→输出。构建R 挡速度矢量图如图14 所示。

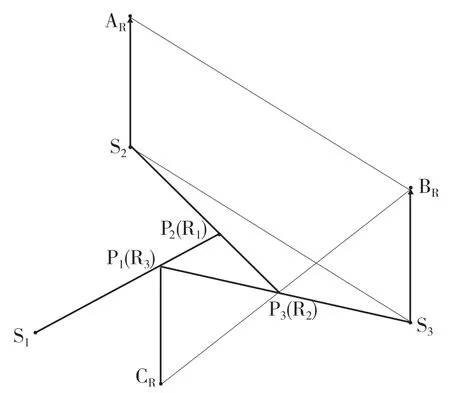
图14 R 挡速度矢量图Fig.14 R gear speed vector

动力由S3输入，从P1（R3）输出，因此R 挡传动比

由相似三角形得

因此R 挡传动比为

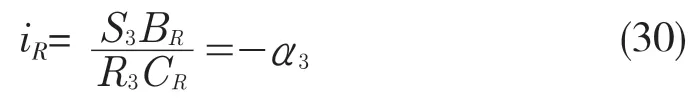
式中“-”表示方向相反。

结合表2 传动比值及传动比式，由D 位4 挡、6 挡、8 挡、9 挡及R 挡建立方程，联立解方程得α1=α2=2.24，α3=2.96，α4=1.61，代入其它传动比验证，结果正确。

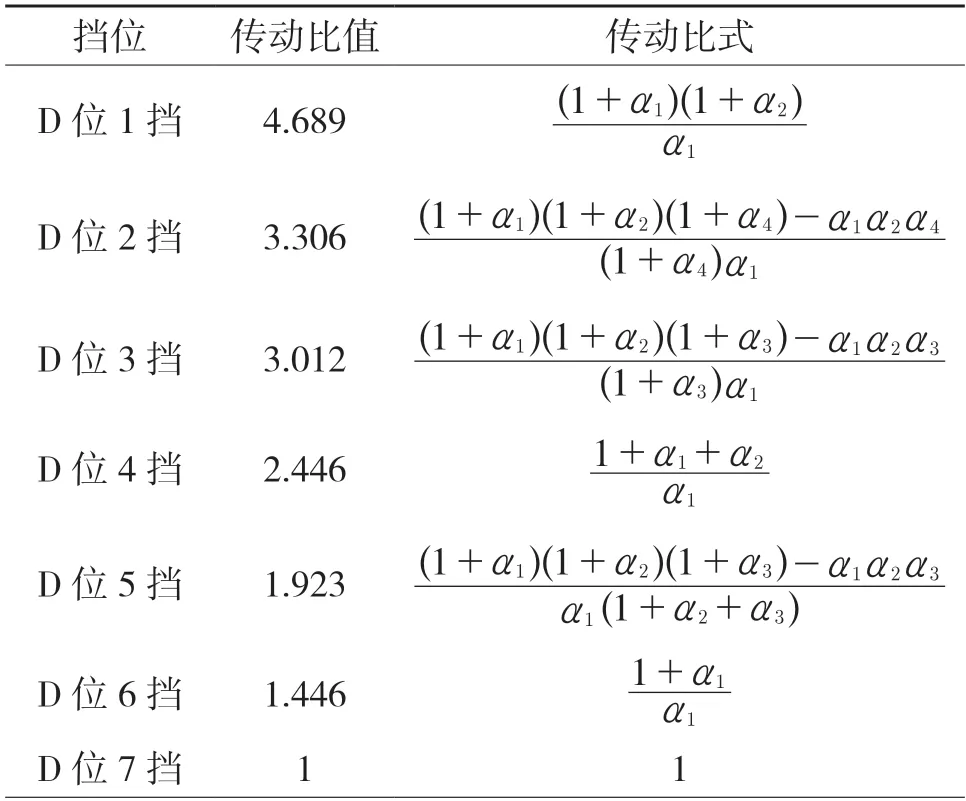
表2 GF9 各挡传动比式及比值Tab.2 GF9 transmission ratio formula and ratio of each gear

（续表）

4 结论

本文通过采用杠杆法，构建基于元件连接平面的空间速度矢量图，利用各挡的运动规律方程和约束条件，推导出各挡传动比公式，并通过传动比分配计算验证了公式的正确性。这种方法对于初学者能更有效直观地掌握自动变速器行星齿轮机构运动情况，为自动变速器的设计和教学提供参考。