适应多负载电池储能系统的拓扑结构优化重构方法

郑良天，康丽霞，2，3，黄贤坤，2，3，刘永忠，2，3

（1 西安交通大学化工系，陕西 西安 710049；2 新能源系统工程与装备陕西省高校工程研究中心，陕西 西安710049；3 陕西省能源化工过程强化重点实验室，陕西 西安 710049）

随着我国动力电池退役潮的来临，如何管理和应用退役电池成为关注的重点。动力电池的梯次利用是将退役电池再利用于对电池性能要求较低的储能应用场景，是一种可行并具有一定经济性的方案。目前，电池回收利用主要是通过拆解电池包提取有用的电芯及其他有价值的材料，但由于电池包拆解工艺复杂度和成本高、存在环境污染以及操作中可能出现的短路、漏液等安全问题，使得对电池包分选后进行整包利用成为一种更经济和安全的回收利用方式。

然而，由于退役电池的使用历史难于跟踪，电池往往存在显著的不一致性，且随着储能系统规模的不断增大，退役电池储能系统的管理面临严峻挑战。近年来，可重构电池网络技术为解决退役电池不一致性的问题提供了新思路。该技术通过变换拓扑结构实现电池间的均衡控制，有效地避免了电池的固定连接设计中由于单体失效而引发的安全故障。Ci等提出利用重构技术动态管理电池系统，可重构系统可以根据电池的当前状态（充电状态和健康状态）实时动态地重构电池拓扑结构，既保证了电池充放电状态的均衡，又具有很强的容错能力。Jeon等在此基础上设计了一种单元串级重构配置方案，通过深度强化学习技术（deep reinforcement learning，DRL）对开关进行了最佳配置，提高了多电池的放电效率。但是考虑到重构系统中的控制对象的细粒度，He等考虑了各单电池的健康状态情况，利用可重构电池网络缓解电池失衡，提高了电池系统交付容量。在这些研究中，电池储能系统的重构大多是满足单一负载需求，关注点在于如何解决电池的不一致性问题。而实际中，电池储能系统的应用场景往往是多样化的，需求端的负载也存在数量和负荷上的差异。因此，如何通过灵活改变电池间的连接关系适应变化的电池状态和负载需求尤为重要。在拓扑变换过程中，如何最大限度地减少控制开关的数量，降低拓扑变换的复杂度以提升可重构系统的安全性也是必须解决的问题。

为此，考虑到可供电压的匹配问题，传统上通常采用稳压器来转换电压输出以匹配负载所需。对于传统的串并联固定的电池储能系统，面向不同负载需求一般是通过稳压器调节。该方法将导致额外的电能消耗；同时，当电池系统供应电压与负载所需电压之间的差异变大或负载变轻时，电压调节器的效率将显著降低。因此，本文提出了一种适应多负载电压需求的低复杂度退役电池包结构优化重构方法。该方法通过构建退役电池包的重构网络优化设计模型，并运用改进的二进制纵横交叉优化算法，可确定退役电池储能系统的拓扑结构及其变换规则，使其能够满足多负载电压的供电需求。本文将通过案例分析验证所提方法的有效性和优越性。

1 问题描述

如图1所示，本文提出的低复杂度重构系统将个退役电池包分为主路和分流结构两部分。主路和分流结构中的支路都由数量不等的电池包串联而成。主路的主要作用是为负载提供满足需求的工作电压，而分流结构的主要作用是通过重组其余电池包以尽可能增加分流支路的数量，从而达到减小电流和降低系统内阻的目的。由图1可见，该系统中的部分电池包将配备旁路开关，以控制电池包的启停状态，而分流结构中的每一条支路都配备一个开关，用以控制支路的启停状态。通过控制这些开关，即可实现不同电池包间的串并联及旁路，形成多种路径组合以适应多种负载需求。

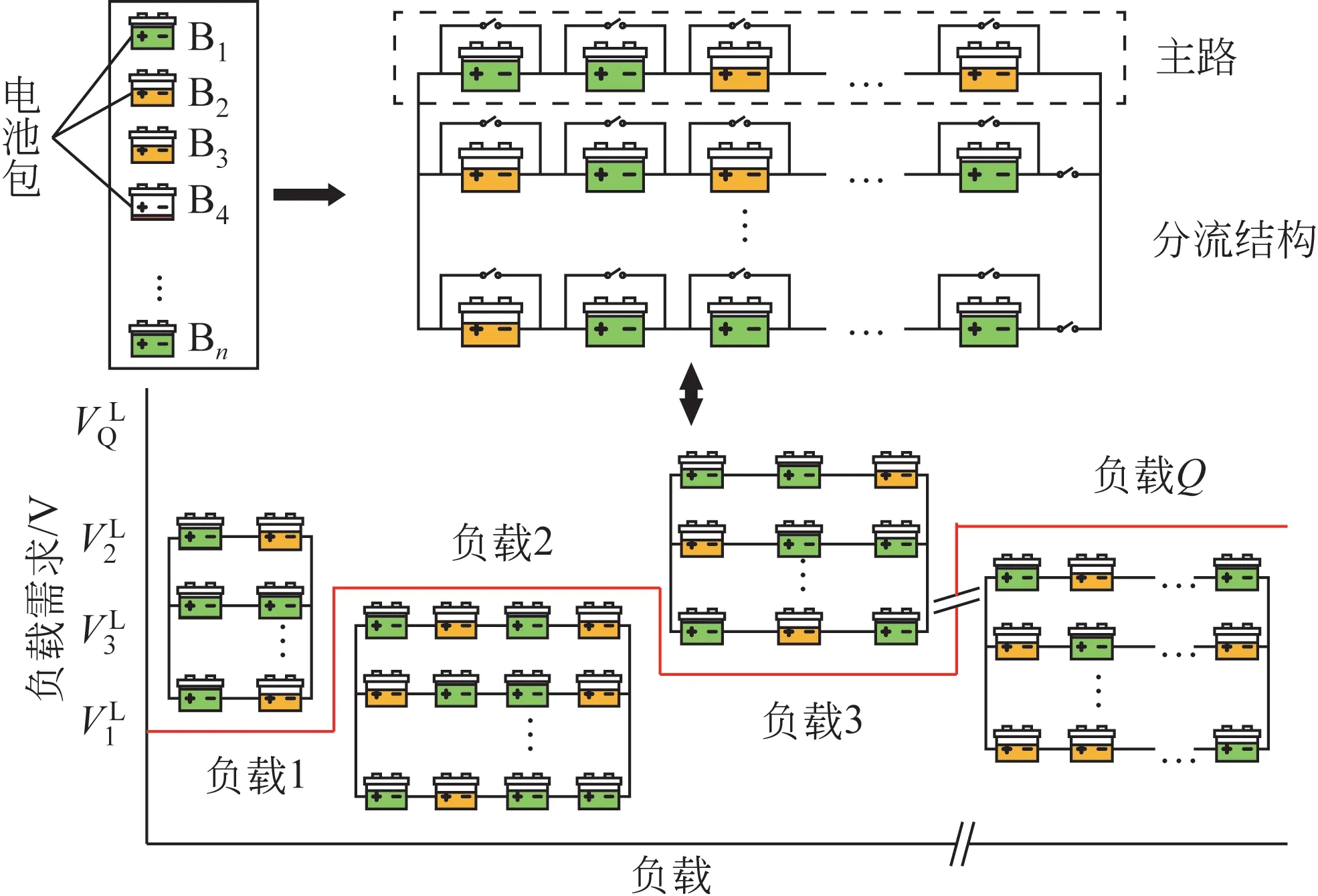
图1 面向多负载的拓扑重构过程示意图

式中，为倍数系数，则此时重构后的电池系统输出电压可满足实际的负载需求。

2 电池储能系统的拓扑重构方法

本文提出的电池储能系统拓扑中包含为负载提供工作电压的主路和用于削减电流的分流结构两部分。该系统的重构设计方法将同时包括主路设计和分流结构优化设计。在本文中，首先根据负荷需求筛选出最优的电池包组合形成主路，然后对剩余电池包进行组合优化以获得能够满足不同负载需求的分流结构。需要注意的是，分流结构电池包的筛选中将优先考虑满足大负载需求，然后在满足大负载需求的可行路径电池包中寻求满足其他较小负载需求的可行路径。

2.1 状态变量

为了便于描述，定义以下状态变量。（1）主路的电池包状态向量，见式(3)。

（2）分流结构中满足最大负载需求的可行路径状态向量，见式(5)、式(6)。

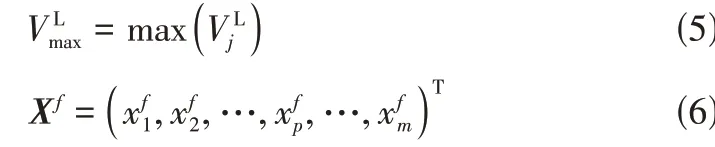
式中，为面向可行路径的序号；为满足需求的可行路径总数；X为布尔向量，表示利用的可行路径；x为分流结构中可行路径的启停状态，具体表示为式(7)。

2.2 电池储能系统的拓扑重构优化模型

2.2.1 目标函数

本文的多负载电池包重构系统优化是一个组合优化问题，也是一个多目标优化问题。优化目标包括：①最小化主路输出电压与负载需求电压间的差异以最大限度保证能源效率和系统安全；②最大化分流支路数以降低流经电池包的电流值，减小内部能量损失；③最小化主路上的电池包数以保证电池包能量利用效率。则最终的目标函数表示为式(8)。

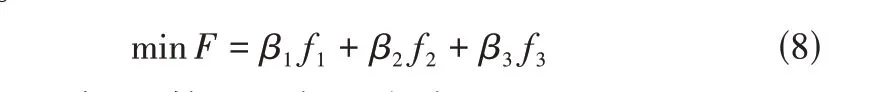
（1）目标函数可表示为式(9)。

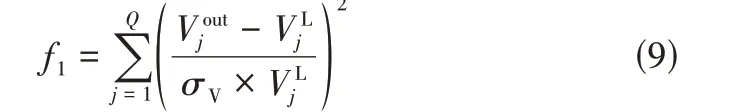
式中，为主路中面向第负载需求时的输出电压；为第负载的需求电压；为允许的抖动电压比。

（2）目标函数可表示为式(10)。

式中，M为第个负载分流结构中的可行路径数；M 为面向第个负载电池包可组成的最大可行路径数。

（3）目标函数可表示为式(11)。

式中，为主路中启用电池包总数；为满足主路最大负载所需电池包数；为可利用电池包总数。

2.2.2 约束条件

（1）电路输出约束。对于电池包组成的可行路径，在满足各负载需求时，为了抑制环流，保证系统安全，需严格控制多路径间的电压差。故可行路径上电池包的总输出电压与负载需求电压之间应满足式(12)。

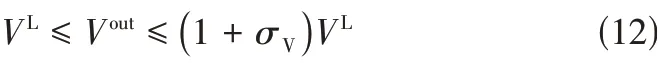
式中，为可行路径上的总输出电压；为可行路径需满足的负载电压；值通常很小，本文取文献[9]中的2.5%。

（2）主路的负载约束。为了适应系统对多负载的供应需求，主路应满足所有负载需求，故对于构成主路的电池包应满足式(13)。

式中，n为满足负载需求电压 需要的电池包数目；x为构成主支路的电池包使用状态，且x满足式(14)。

（3）分流结构的拓扑约束。对于任意一个负载需求，其可行路径组成的分流结构中同一电池包不能被多次利用。则本文定义可行路径矩阵，矩阵中的每一行表示满足负载需求的可行路径，则分流结构的拓扑约束可表示为式(15)。

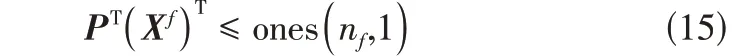
式中，矩阵为可行路径矩阵与启用电池包的关联矩阵；n为主支路确定之后剩余的电池包数目。

2.3 求解方法

本文构建的电池拓扑重构模型是一个离散的线性组合优化问题，属于混合整数线性规划（mix integer linear programming，MILP）问题，也是一个非确定性NP-hard 难题。 而纵横交叉算法（crisscross optimization algorithm，CSO）通过引入横纵双向交叉竞争，有效地避免了群集优化算法（如粒子群算法和遗传算法）中存在的极易陷入局部最优的问题，可显著提高NP-hard问题的求解效率。考虑到状态量的二进制特点，引入Sigmoid函数，通过指引函数决定子代粒子在同一位置取0或1的概率，具体操作以纵向变换为例，如式(16)～式(18)所示，横向变换与之类似。详细的求解流程如图2所示。

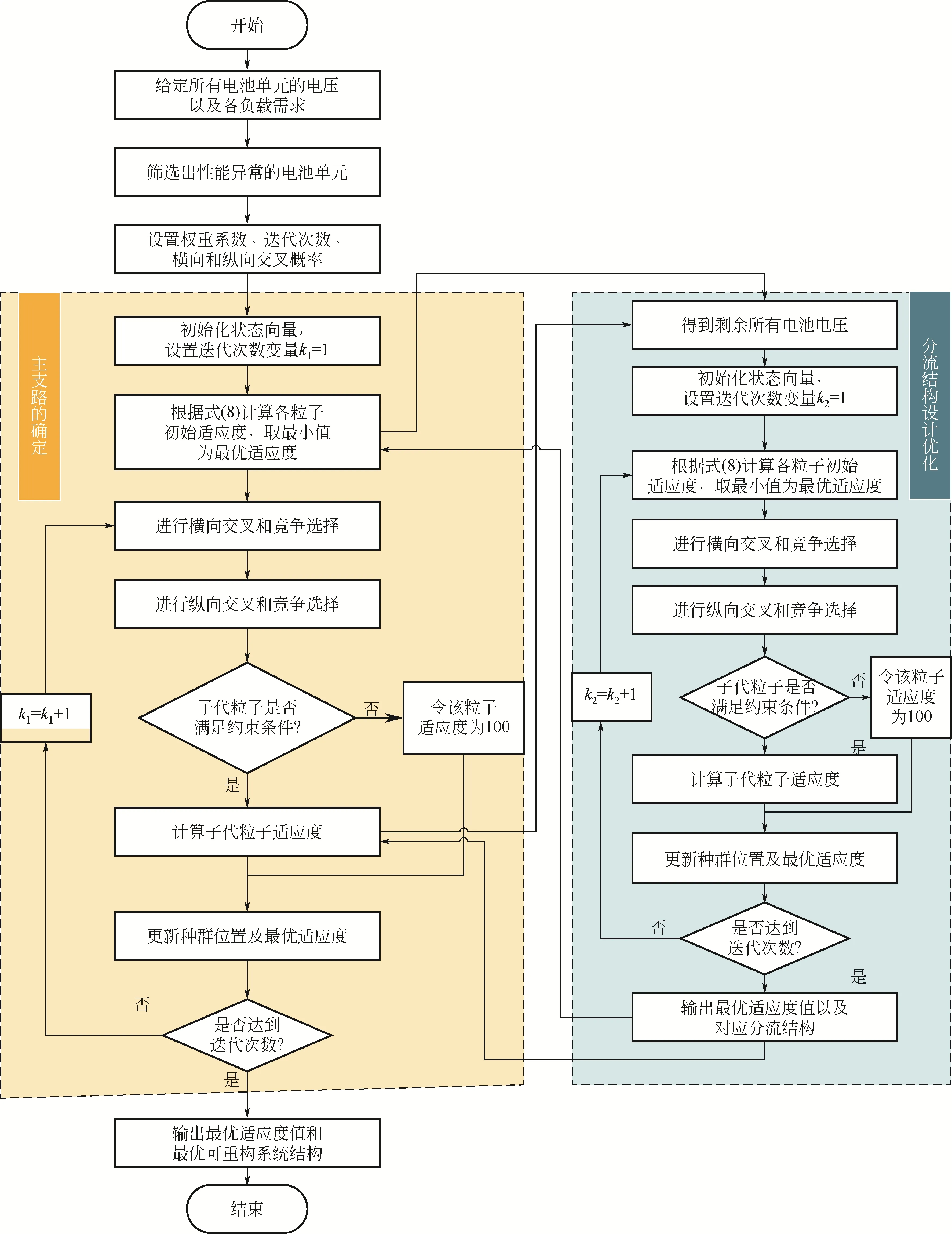
图2 适应多负载需求的拓扑结构优化设计流程图

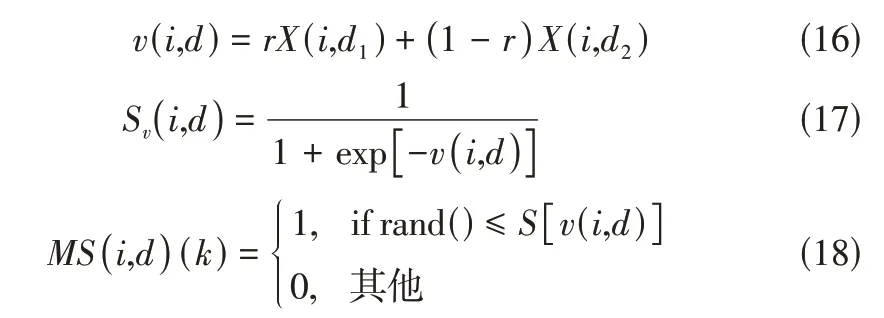
式中，为[0,1]间的随机数；和表示粒子维度；(,)为粒子()的第维和第维纵向交叉产生的子代粒子。

3 案例

3.1 基础数据

本文案例选取同一批次18 个退役电池包，其中16 个电池包的电压范围为[10V, 12V]，即取11V，取1，计算标准差=0.7280，故=13=2.184，即16 个电池包性能相近。另外两个设置为性能偏差较大的电池包，电压分别为5V、8V（如表1所示），负载需求电压、和分别为55V（负载1）、44V（负载2）和33V（负载3）。

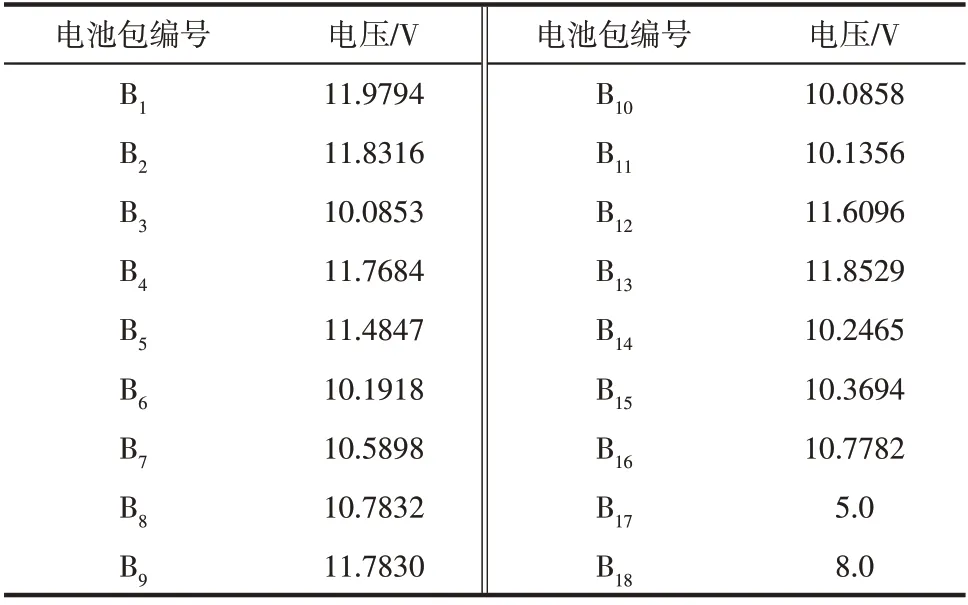
表1 18个电池包的电压值

求解过程中的参数设置如下：目标函数的权重系数、、分别为0.6、0.3、0.1，BCSO算法的迭代次数均为100；BCSO 算法中横向交叉概率都为1，纵向交叉概率都为0.7。BCSO 算法和GA 算法在MATLAB 中编程实现，计算机为Inter(R)Core(TM)i5-8265U CPU@1.60GHz 1.80GHz。

3.2 结果分析与讨论

通过模拟计算得到了满足三负载需求的最优拓扑结构，如图3所示。三种负载需求下对应的电池包拓扑结构如表2所示。

表2 各负载条件下的结构状态

图3中所得的拓扑结构中，16个性能相近的电池包都包括在内。主路上的电池包数量为6个，负载2和负载3下均可与负载1共用至少3个电池包，主路上设置5个旁路开关，整个结构中只需要设置10 个旁路开关就可实现不同负载下的结构变换，大大降低了拓扑变换的复杂度。另外，不同负载下对应的系统拓扑中电池包数量不同，除了负载差异外，主要是因为本文在拓扑设计的过程中允许电池包闲置，大大地降低了最终拓扑结构中电池包的数量和复杂度。

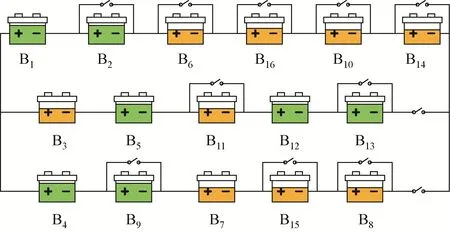
图3 利用拓扑重构方法得到的最优电池系统结构

分析三个负载下对应各支路输出电压可知，在负载1条件下，各支路的输出电压分别为55.0275V、55.1681V、55.2938V；负载2 条件下，各支路的输出电压分别为44.781V、45.0325V、44.5106V；负载3 条件下，各支路的输出电压分别为33.0041V、33.1796V、33.1414V。输出电压与需求电压之间的差异小于2.5%，严格满足式(12)中的约束条件，且输出电压的波动较小，保证了系统的安全稳定操作。在三个负载需求下，各支路输出电压的标准差分别为0.109、0.213、0.075，由此可见，各支路间的电压差异很小，大大抑制了电路间环流电流产生带来的不利影响。从而进一步验证了采用本文方法设计拓扑重构结构电池储能系统的有效性。

图4给出了电池包在三种负载条件下对应的最优拓扑结构。通过对比可见，各结构中启用的电池包数量、种类、位置、连接关系等差异明显。在多负载需求条件下，以下三个结构合并后的主路中将至少包含7个电池包和6个旁路开关。而本文提出的拓扑重构方案不但可直接用于多负载需求场景，还可通过共用电池包，大大降低系统拓扑的复杂度，减少开关数量进而降低控制成本。

图4 各负载条件下的最优结构

此外，观察所获得的最优结构可以看到，在给定权重系数条件下，由于取值较小，电池系统结构更倾向于目标、最优，故主路中的电池包数大于满足最大负载需求所需的电池包数。为了分析权重系数对系统结构的影响，以下将的取值增大到0.6，、分别设定为0.3和0.1，在同样条件下进行求解，得到的结构如图5 所示。由图5 可知，此时主路中的电池包数量为最大负载需求目标下所需的电池包数目。进一步定量研究权值对于最终结构的影响，得到了图6所示关系图，当权值的取值位于图中粉色区域时，算法将会倾向输出图3中的结构，而取值位于绿色区域时，将会倾向得到图5中的结构。因而，在实际应用过程中，可根据需求重点调整权重系数，以获得满意的拓扑重构结构。

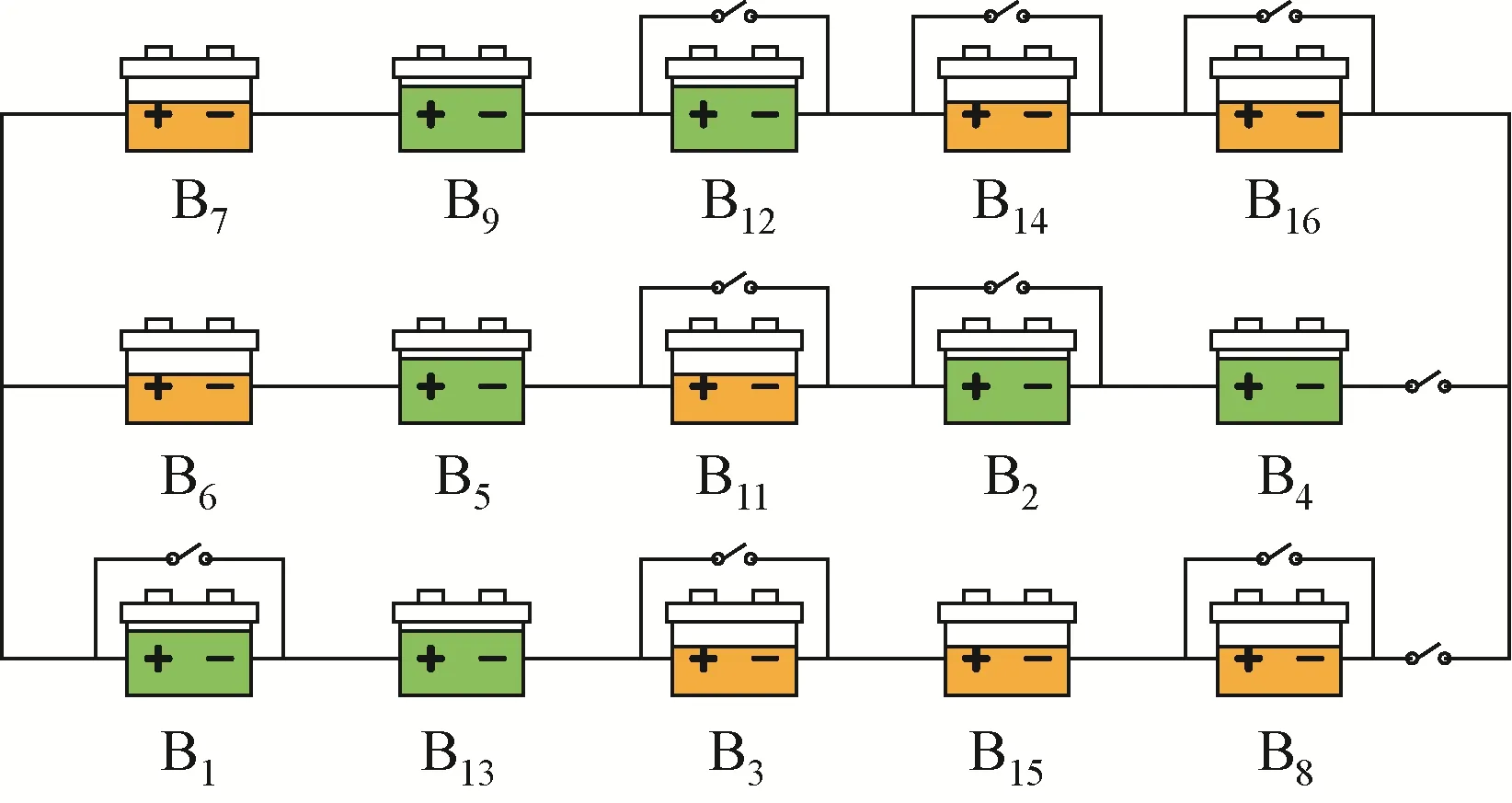
图5 改变权重系数后得到的最优结构

图6 不同权值下两种结构的适应度值关系图

由图7可见，在分析BCSO算法和GA算法与迭代次数的关系时，尽管GA 算法相比BCSO 算法的求解时间稍短，但其容易早熟收敛，而陷入局部最优。而BCSO算法由于纵横双向的交叉竞争，避免了过早陷入局部最优的问题，有效地提高了求解质量，输出了性能更优的可重构电池包结构。因此，同等条件下，BCSO算法相比GA算法更优。

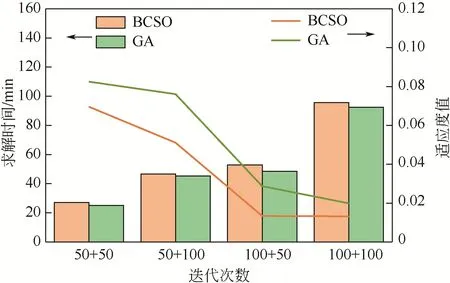
图7 BCSO和GA算法运行时间和适应度变化

4 结论

电池拓扑重构技术为性能不一致的退役电池回收利用提供了高效和经济的途径。本文在给定电池包电压和负载需求的条件下，提出了可适应多负载电压需求的电池储能系统优化重构方法。通过构建可重构电池系统优化模型，采用改进的BCSO算法获得了电池储能系统的拓扑结构及其变换规则，使其能够满足多负载的供电需求，并通过案例分析以及与GA算法的对比研究验证了本文所提方法的有效性和优越性。研究结果表明，本文的电池包拓扑优化重构方法不但可直接用于多负载需求场景，还可通过共用电池包，大大降低系统拓扑的复杂度，减少开关数量，进而降低控制成本。此外，电池包的可重构拓扑结构受优化目标及权重系数影响，实际中应根据需求调整权重系数以获得满意的拓扑结构。

需要说明的是，本文对于电池包特性的评估仅针对电压这一指标，下一步的研究工作将聚焦未拆解的电池包的状态估计以及考虑多因素情况下的拓扑结构动态重构设计。

B—— 电池包

—— 粒子维度

—— 目标函数值

—— 各优化目标函数值

—— 同类电池容许的电压偏差，V

—— 分流结构中可行路径数

—— 子代粒子

—— 可行路径总数

—— 电池包总数目

n、n—— 主路中满足负载所需以及总的电池包数目

n—— 分流结构中电池包数目

—— 可行路径与利用的电池包之间的联系矩阵

—— 可行路径矩阵

—— [0,1]间随机数

—— Sigmoid函数

—— 状态指引函数值

—— 父代粒子

—— 主路状态向量

X—— 分流结构状态向量

—— 主路中电池包使用状态

x—— 分流结构中可行路径使用状态

—— 倍数系数

—— 权重系数

—— 电压标准差

—— 容许的抖动电压比

、—— 电池包序号

—— 负载需求序号

—— 可行路径序号