基于无人机与卡车协作的封控社区生活物资配送方法

季金华，刘亚君，别一鸣，王琳虹

(吉林大学，交通学院，长春 130022）

0 引言

自2020年1月以来，新型冠状病毒肺炎疫情已经在全球范围内肆虐超过2年时间。随着病毒的不断变异，其隐匿性和传播力逐渐增强，感染者的症状逐渐变轻，导致很难及时诊断出阳性患者。尤其是自2021年底以来，传播速度更快的德尔塔和奥密克戎变异毒株席卷全球，容易悄无声息地造成大规模人群感染。为了及时阻断病毒传播，减少感染人群数量，中国政府不得不先后在西安、吉林市、长春及上海等城市采取严格的封控管理措施。在此期间，当地政府安排志愿者或者社区工作人员为各个小区的居民配送生活物资(以蔬菜包为主)，维持基本生活需求。

然而，根据上述城市的经验，从采取封控管理至恢复正常生产生活秩序至少需要30 d的时间，即使全市采取封控较长时间后仍然会出现感染人数大幅度增加的情况。以长春市为例，该市于2022年3月11日采取封控管理，但是，在2022年4月5日全天仍新增确诊病例817例，无症状感染者1682例。主要是因为：(1)封控管理期间本地蔬菜批发市场工作人员中出现感染病例，当携带新冠病毒的蔬菜包被送至各个小区后，造成病毒在小区内的传播；(2)各个家庭需要派人前往小区门口提取蔬菜包或其他生活物资，由于很多小区面积大和人口多，在小区内部走动时容易出现居民之间的交叉感染；(3)社区工作人员和志愿者在工作(例如核酸检测和配送生活物资)期间被感染，之后，造成病毒在社区内传播。为了迅速遏制感染人数快速增加的局面，当地政府只能不断升级疫情管控措施，减少物资与人员的流动，导致市民生活物资普遍出现蔬菜短缺的问题，造成了严重的社会负面影响。

此外，在封控管理期间，社区工作人员与志愿者承受着严重的身体与精神压力，尤其当一个小区出现病例后，该小区所有人员均需要居家隔离，由社区工作人员或者志愿者将小区门口的生活物资分送至各个家庭，导致他们的工作量急剧增加，疲惫不堪，经常出现由于人力资源紧张导致物资无法及时配送的情况。实施封控管理的城市人口规模巨大(例如上海市超过2500万人，西安市超过1000万人)，为了维持城市的基本运转需要数量庞大的志愿者队伍，但是，当疫情严重时，志愿者招募困难，导致出现人力不足的情况。例如，2022年4月9日上海市政府指出：封控管理期间人员和运力缺乏是导致物资配送最后一公里和最后一百米矛盾突出的主要原因[1]，此时，上海市已经处于严格的封控管理状态超过10 d。

由以上分析可知，生活物资被病毒污染，小区内交叉感染及人力短缺是突发重大公共卫生事件情况下采取封控管理措施的城市所面临的共同问题。为了解决这些问题，本文提出一种基于无人机与卡车协作的社区生活物资配送方法。例如，在城市A采取封控管理的情况下，由未发生疫情的相邻城市B 对城市A 进行生活物资的支援。一辆卡车在城市B装载生活物资后，直接行驶至城市A的一个社区。由卡车司机或者社区工作人员采用无人机将生活物资依次送至各个居民楼，居民通过手机APP实时查询无人机的位置以及预计送达时刻；无人机将生活物资送至居民楼下后飞离，然后，居民下楼将物资取回。当无人机返回卡车所在位置后，由工作人员对其进行消杀，之后，接着运送生活物资。这种配送方法具有如下优势：首先，A 城市居民得到的生活物资均由未发生疫情的城市B提供，避免了携带新冠病毒的生活物资导致居民感染；其次，居家隔离人员下楼就可以直接拿到生活物资，无需步行至小区门口，避免了小区居民的交叉感染；然后，当无人机电量即将耗尽时，只需要更换电池就可以使其连续工作，所需的社区工作人员或者志愿者数量大幅度减少，而且大大降低了他们的体力工作量；最后，无人机方便消杀，避免生活物资配送过程造成的病毒传播。

已经有学者提出了采用无人机与一辆或多辆卡车协作进行大范围内物流快递配送的研究，主要以配送时间或者配送成本最小为目标建立配送路径优化模型[2]，配送过程中无人机可以在一次飞行中携带多个包裹[3]或者服务多个顾客点[4]。张洪海等[5]综合考虑无人机性能、任务性质和城市环境等影响，以续驶里程、高度变化和危险度最小为目标函数，构建多约束物流无人机路径规划模型。借助无人机停放平台，蒋丽等[6]考虑包裹异质性以及无人机在不同配送阶段的精确能耗，构建以飞行成本和能耗成本最小为目标的高层住宅配送模型，解决“垂直位置最后一百米配送”问题。彭勇等[7]将客户分为只能由卡车服务的客户、只能由无人机服务的客户以及卡车与无人机均能提供服务的客户这3类，以车辆总服务时间最小为目标，建立车辆与无人机协同配送模型。考虑无人机限载、电量及客户时间窗等约束，胡觉亮等[8]建立了一辆卡车搭载多架无人机为客户进行配送的混合整数规划模型。郭秀萍等[9]考虑无人机续航里程约束和装载量限制，提出一种卡车-无人机联合配送模式，并设计了一种三阶段规划求解方法。承琦等[10]在无人机运载能力和飞行半径的约束下，使用Mean-Shift算法和改进模拟植物生长算法获取无人机最优集结点及最短运输路线。WANG 等[11]针对多辆卡车与多架无人机协同配送问题，提出了一种混合整数规划模型，并采用分支定价算法进行求解。COINDREAU等[12]提出了混合整数线性规划模型和自适应大邻域搜索处理由卡车和无人机同时使用而造成的约束数量增大的问题。此外，无人机与卡车协同配送模型还被广泛应用于血液供应链[13]和救灾行动[14]的最后一公里配送问题中。

综上，现有研究并未考虑突发公共卫生事件下社区封控管理对无人机与卡车协作配送问题的影响。已有的研究方法不再适用，主要是因为：(1)在突发公共卫生事件下，无人机每次只能服务一个家庭，并在完成每次配送后需要返回卡车位置处进行消杀；(2)为避免交叉感染，应尽可能延长同一居民楼单元不同家庭下楼取走生活物资的时间间隔；(3)卡车在社区中所停靠的位置对配送时间、配送成本以及无人机的运行路径存在较大影响，需要进行优化，而在传统物流配送中，物流仓库的位置(类似于本文中的卡车停放位置)是固定且已知的。为此，本文面向采取封控管理的城市社区，提出一种基于无人机与卡车协作的生活物资配送方法，建立以配送过程中社区居民交叉感染风险和配送成本最小为优化目标的混合整数规划模型，协同优化卡车额定载重、停靠位置、所需无人机数量以及无人机组配送方案，采用改进多目粒子群算法进行求解，并以长春市师范南园小区为例对该方法的应用进行说明。

1 封控社区生活物资配送

1.1 问题描述

在突发公共卫生事件情况下，城市A的1个指定封控管理社区内居民的生活物资由来自于未发生疫情的城市B的1辆卡车及其携带的多架无人机负责配送，城市A其他封控管理社区的生活物资由来自未发生疫情的城市B 或者其他城市的其余卡车及其携带的多架无人机负责配送。当卡车到达城市A停靠在指定社区的d处后，由卡车司机或者社区工作人员采用其携带的无人机组K将生活物资依次送至各个住户。其中，d∈D，D为封控管理社区内方便卡车停靠位置集合，停靠位置可以是广场、大院及较宽的主干道；卡车携带的无人机数量由社区内存在生活物资需求的住户数量和无人机组配送方案决定；卡车额定载重Q′由社区内所需的物资总重量、无人机组重量以及消毒产品重量之和共同决定。假设每架无人机在开始全天配送任务时电池剩余电量均等于。

存在生活物资需求的住户i需要通过手机APP提前上报生活物资需求(i∈I)，所需物资的时效性等级ai与生活物资种类有关，例如，药品和冷冻食品的时效性等级较高，时效性等级ai取值越小。住户i所需生活物资的时效要求越高，规定最晚送达时刻越小；为卡车停靠位置d与住户i之间的无人机配送欧式距离。

无人机在封控社区内的配送过程可描述为：无人机k(k∈K)在时刻携带消毒后的生活物资从卡车停靠位置d起飞，向住户i配送生活物资，为无人机k装载物资由卡车停靠位置d飞往住户i的配送时长(s)。为了避免社区居民的交叉感染，规定无人机k在结束住户i的配送任务后，需要空载返回卡车停靠位置d，为无人机k空载由住户i飞往卡车停靠位置d的配送时长(s)。无人机返回卡车停靠位置d后，由操控员为无人机k消毒，每次消毒所需时间为，并判断无人机k的电池剩余电量是否足够继续为下个住户j(j∈I，i≠j)配送生活物资，并顺利返回。若电池剩余电量不足，则需要为无人机k更换电池，为无人机k更换电池所需时间(s)。假设充电设施数量充足，被更换下来的电池立即安排充电且无需排队，直至充满才允许被使用，则无人机每次更换电池后电池剩余电量等于电池额定容量。

模型的重要符号和参数定义如表1所示。

表1 符号和参数定义Table 1 Definition of symbols and parameters

1.2 目标函数构建

对于采取封控管理的城市社区，无人机组配送方案(包括每架无人机服务的住户编号、配送次序及等待时长)不仅会直接影响住户间的交叉感染风险，还会与卡车额定载重、停靠位置和无人机数量一起影响配送时长和配送成本。因此，本文以配送过程中社区居民交叉感染风险和配送成本最小为优化目标，优化卡车额定载重、停靠位置、所需无人机数量及无人机组配送方案。

令二进制变量∈{0,1}，当卡车停靠在位置d时，无人机k在服务完住户i后服务住户j，则1；否则，0。二进制变量∈{0,1}，如果无人机k在结束服务住户i返回卡车停靠位置d后需要更换电池，则1；否则，0。当无人机k不服务住户i，则为无人机k在服务完住户i后(开始服务住户j前)在卡车停靠位置d的等待时间。

由于无人机每次返回卡车停靠位置和生活物资被送往住户前均需严格按照防控要求消毒，认为该环节中病毒传播风险可控且可忽略不计。生活物资实际送达时间受无人机组配送方案影响，住户在下楼取走生活物资过程中可能会与同一居民楼单元内其他住户时空重叠，存在交叉感染风险。本文采用社区内住户之间的时空重叠次数总和量化交叉感染风险。当同一居民楼单元n内任意住户i与住户i′(∀ni=ni′,i≠i′)收到由无人机k或者k′配送生活物资的时刻差值小于，即，时，认为住户i与住户i′存在时空重叠，记作Fi,i′=1。当同一居民楼单元n内任意住户i与住户i′满足，或者住户i与住户i′属于不同居民楼单元(∀ni≠ni′)时，认为住户i与住户i′不存在时空重叠，记作Fi,i′=0。则无人机配送过程中社区居民交叉感染风险Z1为

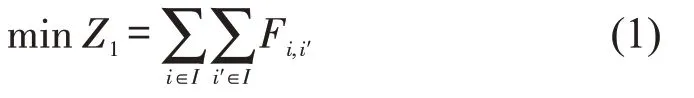
配送成本Z2包含无人机购置成本(不含电池)、操控员用工成本、电池购置成本、能源消耗成本、卡车运输成本以及易逝品的损耗成本。无人机购置成本(不含电池)和操控员用工成本，随着实际投入使用的无人机数量和配送时长增加，两项成本逐渐增大。无人机电池购置成本由无人机数量、更换电池时间及电池充电功率共同决定。当无人机往返卡车与各个住户的配送时长与载重已知时，无人机能源消耗成本仅与卡车停靠位置有关。卡车运输成本由卡车额定载重和运输距离共同决定。易逝品的损耗成本与生活物资种类有关。配送成本为

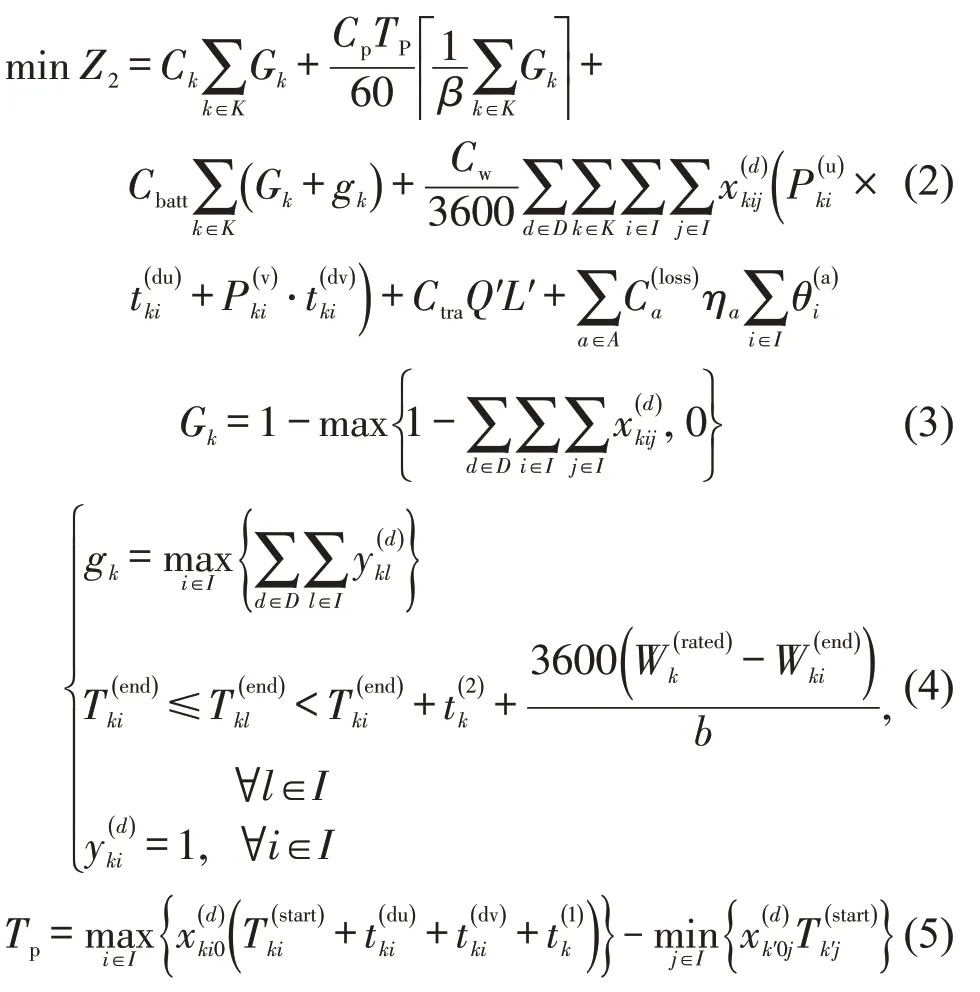
式中：Ck为无人机单价(不含电池)(元·架-1)；Cp为无人机操控员工时成本(元·h-1)；Cbatt为无人机电池单价(元·个-1)；Cw为无人机k的能耗单价(元·kWh-1)；Ctra为卡车运输单价(元·kg-1·km-1)；为时效性等级a类物品的损耗单价(元·个-1)；L′为卡车运输距离(km)；ηa为时效性等级a类物品的损耗率(%)；为社区内时效性等级a类物品的需求量(个)；A为生活物资时效性等级的集合；Gk∈{0,1}，Gk=1 表示无人机k投入使用，否则为0；gk为无人机k的备用电池数量(个)；β为每位无人机操控员可以同时操作无人机数量最大值(架)；Tp为无人机操控员工作时长或者无人机组配送时长，等于所有投入使用的无人机组(∀k∶Gk=1)结束配送任务，返回卡车停靠位置的最晚时刻与开始服务住户的最早时刻之差(min)；为向上取整函数；为无人机k装载住户i所需物资后的飞行功率(kW)；为无人机k空载(qi=0)的飞行功率(kW)；b为无人机电池充电功率(kW)；为无人机k结束服务住户i返回卡车停靠位置d完成消毒的时刻，为无人机k结束服务住户i返至卡车停靠位置d时电池剩余电量(kWh)；为无人机k结束服务住户i后更换下来电池的充电时长(h)；l为无人机k在充电时间窗口内服务的住户编号；∈{0,1}，当无人机k结束服务住户l(l∈I)返回卡车停靠位置d后需要更换电池，则1，否则为0。

1.3 混合整数规划模型建立

本文以社区居民交叉感染风险Z1和配送成本Z2最小为目标，建立混合整数规划模型，相关约束条件为

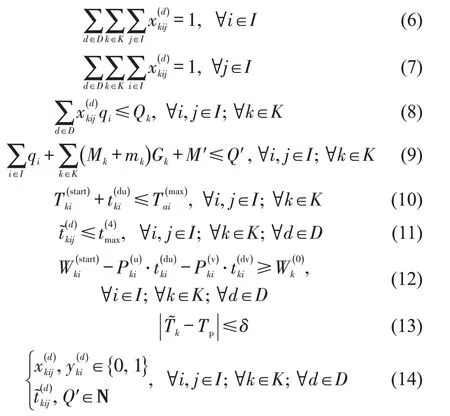
式中：Mk为机身重量(kg)；mk为电池重量(kg)；M′为车载消毒产品的重量(kg)；为无人机k开始服务住户i时电池剩余电量(kWh)。为无人机电池剩余电量安全阈值。

式(6)和式(7)保证每个住户的生活物资需求均会被满足；式(8)规定无人机k每次装载的物资重量不得超过其载货重量限制Qk；式(9)规定卡车的额定载重需大于社区内所有住户所需的物资重量、无人机组重量以及消毒产品重量之和；式(10)保证住户i收到由无人机k配送生活物资的时刻要小于等于规定值；式(11)要求不得超过规定最大值；式(12)保证无人机电池剩余电量足够结束服务住户i并安全返回卡车；式(13)要求无人机k的配送时长与无人机组配送时长Tp的绝对差值要小于等于固定值δ；式(14)为优化变量取值情况。

除上述约束外，无人机k服务的任意相邻配送任务之间的时间关系应满足：无人机k开始服务住户j的时刻等于无人机k结束服务住户i并返回卡车的时刻加上无人机k服务的任意相邻配送任务之间的电池剩余电量关系应满足：若0，无人机k开始服务住户j时电池剩余电量等于结束服务住户i时电池剩余电量；若1，无人机k开始服务住户j时电池剩余电量等于。

2 算法设计

2.1 算法描述

本文建立的模型是多目标混合整数规划问题，属于NP-hard 问题。两个目标函数之间相互制约，为了降低小区内交叉感染风险，减少社区内住户之间的时空重叠次数，需要调整无人机的配送次序并延长等待时间，甚至需要增加投入使用的无人机数量，进而导致无人机组配送时长延长和配送成本增加，因此，可能无法存在使得两个目标函数同时最优的解，但存在Pareto最优解。多目标粒子群算法通过产生多个粒子在搜索空间中同时搜索个体最优解，并将当前个体位置与速度与整个粒子群共享，可以帮助快速找到当前全局最优解，但也容易导致陷入局部最优解。本文采用一种特殊的粒子编码方式，并耦合变异算子更新部分码位粒子的位置，改进多目标粒子群算法的收敛性和多样性，适应建立的突发公共卫生事件下无人机与卡车协作的封控社区生活物资配送模型。

2.2 改进多目标粒子群算法步骤

Step 1 设置迭代次数h=1。确定算法基本参数，包括粒子种群大小θpop，外部档案集Up的大小θrep，最大迭代次数H。

Step 2 将卡车停靠位置、无人机组服务住户编号及配送次序分配方案编码为粒子将I个住户分为K个批次进行配送，每个批次由一架无人机进行配送，S′1表示每个批次内服务的住户编号及顺序，并用0值区分各批次，S′1采用整数编码并包含I+K-1 个码位。S′2表示执行S′1中对应批次配送任务的无人机编号的集合，S′2采用整数编码并包含K个码位。S′3共包含I个码位，采用整数编码，依次表示无人机为第j个用户配送前的等待时间。表示卡车位置编号，采用整数编码，包含1个码位。

Step 3 随机初始化粒子，通过求解模型计算各个粒子的适应度值，适应度函数由标准化后的目标函数和用于处理约束的罚函数共同组成。将非劣解加入到外部档案集Up中。采用拥挤度维护外部档案集，当档案集中解的数量超过其大小时，根据自适应网格方法进行筛除。

Step 4 确定粒子初始最优位置，在不能严格找到两个目标函数(例如式(1)和式(2)所示)同时更好的粒子时，随机选择其中一个作为当前最优位置。然后，基于拥挤度(尽量选择不那么密集位置的粒子)为每个粒子选择1 个合适的群体最优位置。

Step 5 更新粒子对应S′1，S′2，S′3和的位置。基于常用惯性因子和加速因子更新每个粒子的和的速度和位置。基于交叉算子对每个粒子的S′1和更新位置。将粒子本身的S′1和作为父代1 号，以的概率接受粒子本身逆序，当前最优位置和，群体最优位置和作为父代2 号。w为惯性权重，c1和c2为加速因子。对于S′1，随机选择区间[1,I+K-1]内的两个码位O1和O2进行交叉操作，即更新后粒子的S′1上码位O1和O2的数字与父代2相同，其余码位与父代1相同。类似地，对于S′2，随机选择区间[I+K,I+2×K-1]内的两个码位O3和O4进行交叉操作，即更新后粒子的S′2上码位O3和O4的数字与父代2相同，其余码位与父代1相同。

Step 6 令h=h+1。如果迭代次数大于H，则输出外部档案集；否则，返回Step 4。

3 算例分析

3.1 数据获取

以长春市师范南园小区为例，测试本文建立的封控社区生活物资配送模型。小区内有147 个住户存在生活物资需求，分属于26 个居民楼单元。两个社区入口分别位于小区的西北侧和东北侧。当卡车停靠在小区东北侧入口，记作d=1；当卡车停靠在小区西北侧入口，记作d=2。小区内居民楼单元与小区入口之间的无人机配送欧式距离如表2所示。

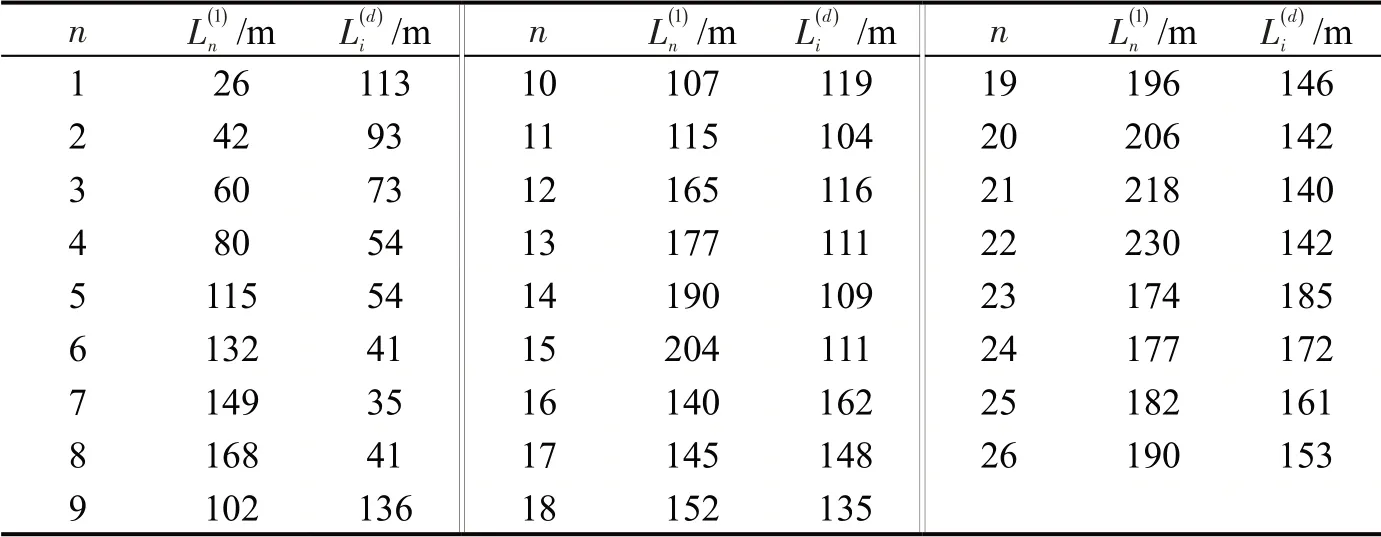
表2 各居民楼单元与小区入口之间的无人机配送欧式距离情况Table 2 Euclidean distance between residential building units and community entrances

将无人机组开始配送任务的时刻记为0。住户通过手机APP 提前上报的生活物资需求共包含3种时效性等级。药品和冷冻食品的时效性等级最高，重量约为0.2～2.0 kg，规定最晚送达时刻为3600 s；团购蔬菜包的时效性等级次之，重量均为5.0 kg，规定最晚送达时刻为10800 s；一般生活用品的时效性等级最低，重量为0.5～3.0 kg，规定最晚送达时刻为14400 s。3 种时效性等级生活物资的需求占比分别为6.0%，60.5%，33.5%，平均损耗率分别为0.83%，0.50%，0.20%，平均损耗单价为50，30，20元。

注：无人机巡航高度50 m，起飞速度约7.8 m·s-1，降落速度约3.9 m·s-1。

除生活物资外，卡车最多可携带10架无人机，k=1,2,…,10，均配备6S 22.2 V 锂电池。无人机k的电池额定容量0.27 kWh，载货重量限制Qk=6 kg，机身重量Mk=2 kg，电池重量mk=1.5 kg，车载消毒产品重量M′=3 kg，安全阈值0.03 kWh，巡航高度50 m，起飞速度约7.8 m·s-1，降落速度约3.9 m · s-1。无人机机身单价Ck=20000元·架-1，无人机操控员用工成本Cp=20元·h-1；无人机电池单价Cbatt=950 元·个-1，能耗单价Cw=0.525 元·(kWh)-1。假设运输生活物资的卡车来自梅河口市，卡车运输平均单价Ctra=2元·(km·t)-1，运输距离L′=180 km。

每位无人机操控员可以同时操作4架无人机，即β=4。操控员在卡车停靠位置d为无人机k消毒时间=60 s，更换电池时间=180 s。被更换下来的无人机电池充电功率b=0.54 kW。当同一居民楼单元内任意两个住户收到生活物资的时刻差值大于300 s，即=300 s时，认为不存在时空重叠。无人机k每次在卡车停靠位置d的等待时间不得超过300 s，即=300 s。每架无人机的配送时长与无人机组配送时长的绝对差值要小于等于30 min，即δ=1800 s。

3.2 优化结果展示

使用Python 3.8 求解本文建立的模型，数值实验是在Window 10 环境下的Intel(R) Core(TM) i5-9400 CPU@2.90 GHz CPU，内存16 GB 的个人电脑上完成的。令粒子种群θpop=300，外部档案集θrep=60，最大迭代次数H=60。改进多目标粒子群算法在372 s 内找到Pareto 最优解集，输出算法迭代过程中历史Pareto解取值情况如图1所示。

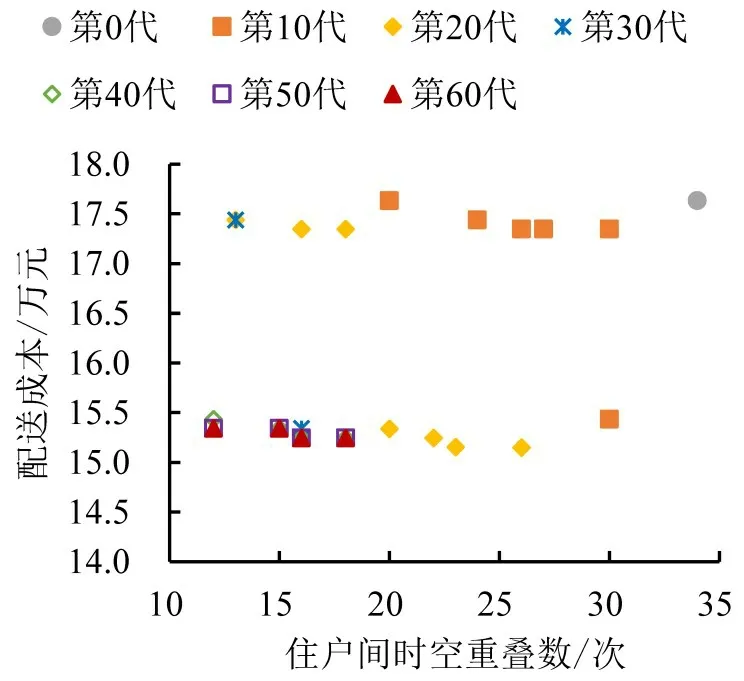
图1 算法迭代过程中历史Pareto解取值情况Fig.1 Historical Pareto optimal solutions during algorithm iteration

由图1可知，随着迭代次数的增加，历史Pareto解集向配送成本和住户间时空重叠次数更小的方向逼近，并在第40代开始逐渐形成pareto前沿。第60代Pareto解集如图中三角形标记所示，其住户间时空重叠数最小值和配送成本最小值与第40 代Pareto解集相同。

优先选择配送过程中社区居民交叉感染风险更低的解作为最优解，则无人机最优配送成本为131743.9 元，包括：无人机购置成本(不含电池)120000.0元，操控员用工成本107.1元，电池购置成本11400.0 元，能源消耗成本1.8 元，卡车运输成本216.0元以及易逝品的损耗成本19.0元。住户间时空重叠次数为12次。实际需6架无机人和12块电池投入使用，卡车额定载重为0.6 t，停靠在小区西北侧入口位置(d=2)。无人机组服务的住户编号及顺序情况如表3所示。

表3 无人机组服务的住户编号及顺序情况Table 3 Household numbering and sequence of drone services

为降低同一居民楼单元内任意两个住户间的时空重叠，无人机在卡车停靠位置需要等待，无人机组的总等待时长为26870 s。时效性等级为1 的物品在2527 s 内全部送达，时效性等级为2 的物品在8666 s内全部送达。无人机3最早完成全天配送任务，配送时长为8903.7 s，无人机1最晚完成全天配送任务，配送时长为10661.1 s

3.3 对比分析

在输入参数取值不变情况下，对比分析卡车与无人机协作配送(模式I)和卡车与人工协作配送(模式II)两种模式。在模式II中，配送人员往返于各单元楼与入口之间的曼哈顿距离要大于模式I中无人机的欧式配送距离，且配送人员的步行速度要小于无人机的飞行速度。假设配送人员搬运生活物资时的平均步行速度为1.1 m·s-1，空手平均步行速度为1.3 m·s-1。在不考虑同一单元楼住户间的时空重叠要求，仅满足式(6)和式(7)以及式(9)和式(10)情况下，需要至少投入人工配送人员4人连续工作。

在安全方面，模式I 中的社区居民交叉感染风险可以通过延长无人机在卡车停靠位置的等待时间降低，但模式II中人工配送人员与住户之间的交叉感染风险是无法避免的，即使完全避免同一单元楼内住户间的时空重叠，仍存在147次与配送人员的直接接触。与模式II 相比，模式I 中社区居民交叉感染风险降低了至少91.8%。

在配送成本方面，除了两种模式均存在的卡车运输成本以及易逝品的损耗成本外，模式I 的配送成本由无人机购置成本(不含电池)、电池购置成本、操控员用工成本和能源消耗成本组成。考虑到无人机机身和电池可以被反复使用，假设无人机机身使用年限为5年，电池使用年限为3年，则模式I 的无人机组日配送成本为185.06 元。模式II 的配送成本等于配送人员用工成本，考虑到疫情期间配送人员招募困难导致的溢价现象，令配送员与无人机操控员的工时成本相同，则模式II的日配送成本约为222.58 元。与模式II 相比，模式I 的日配送成本降低了16.9%。

在工作强度方面，模式II 中的4 名配送人员每人平均需要负重行走约3743 m(不包括由各住户返回卡车停靠位置的步行距离)。相比之下，模式I所需的人力资源投入减少50%，同时，无人机操控员仅需要承担换电池和消毒等简单工作，大大降低了体力工作量。

在一次性防控物资消耗方面，两种模式均需配备生活物资外表面消毒产品和人员防护设备，其购置成本分别与需要配送的住户数量和操控员或者配送员的数量成正比。参照市场价格，包含一次性医用口罩、隔离衣、鞋套、面罩及护目镜等在内的防护设备单价约为127.5 元·套-1。模式I 还需准备无人机消毒产品，参考市场价格每日20 元左右。综合来看，与模式II相比，模式I可以节约46.1%左右的一次性防护物资支出。

综上所述，卡车与无人机协作配送模式在保证封控社区居民生活物资正常供应的前提下，可以有效节约人力资源，提高配送效率，降低配送成本和一次性防控物资消耗，最大程度减少人员接触，降低病毒传播风险。

4 结论

本文提出一种基于无人机与卡车协作的生活物资配送方法，设计改进多目标粒子群算法进行求解，并以长春市师范南园小区为例进行案例分析，发现改进多目标粒子群算法获得的历史Pareto 解集会向配送成本和住户间时空重叠次数更小的方向逼近，在第40 代开始逐渐形成Pareto 前沿，并在342 s内找到Pareto最优解集，求解速度在大中型算例中表现出较佳性能。从安全、配送成本、工作强度及一次性防控物资消耗等4 方面和卡车与人工协作配送模式进行比较分析发现，卡车与人工协作配送方法可以令社区居民交叉感染风险降低至少91.8%，日配送成本降低16.9%，人力资源投入减少50%，一次性防护物资支出节约46.1%左右。