基于改进社会力的单向流电动自行车行为建模研究

王维莉，卢晓磊，张旺，熊浩然，余冕

(上海海事大学，物流研究中心，上海 201306）

0 引言

电动自行车作为短途通勤手段，由于其灵巧便捷、高效省力，已在许多国家被广泛使用。据中国自行车协会统计，截至2020年11月20日，中国电动自行车社会保有量近3 亿辆。大量涌现的电动自行车给交通管理者和道路使用者带来了巨大的挑战和影响。尽管很多城市建有非机动车道或自行车专用道，但电动自行车速度快，骑行者素质参差不齐，随意变道和超越等行为，降低了交通系统的效率，也给道路交通安全带来巨大隐患。

目前对自行车和电动自行车的研究主要集中于交通运行特征[1]、速度分布和自行车道通行能力[2]，较少关注自行车与电动自行车的微观行为。按建模方法将自行车的微观行为分为基于规则的模型和基于力的模型[3]，Li 等[4]考虑自行车与电动自行车属性的异质性，利用与前方被超越车辆的横向间距、纵向安全间距等特征差异提出了一种新的基于规则的元胞自动机模型，研究电动自行车在遇到路边停放的机动车、前方行驶较慢的自行车等不同障碍物的两种非法变道形式。行人研究领域较为成熟的社会力模型[5]在基于力的模型中得到广泛应用，严巧兵[6]建立了具有超越力的改进社会力模型，并对不同边界作用强度、超越向量等关键参数做了标定，但模型仅建立在力学基础上。借鉴行人行为研究中的分层结构，许多学者在基于力模型的基础上引入行为层和操作层对电动自行车微观行为进行两层建模，Gavriilidou 等[7]将非机动车的行驶行为分为心理和物理两个层面，心理层面包括路径选择等行为，物理层面主要是运动行为，利用在荷兰阿姆斯特丹信号交叉口收集的自行车轨迹数据，对两层模型进行了标定，并对排队等红绿灯的骑行者行为属性进行了研究。Liang 等[8]考虑骑行者的反应范围和感知范围建立心理-生理力(PPF)模型，同时在心理层提出通过比较可用空间密度大小来选择骑行行为的轨迹选择模型(TCM)，并认为行为选择是在感知范围内考虑避碰而产生的附属力合力。Li等[9]在上海的十字路口对高密度非机动车混合流建立了动态边界模型，通过分析不同交通环境下横向动态特性确定非机动车与动态边界左右侧净距，结合速度差等交通特性对社会力模型进行改进，建立决策层与操作层模型，在决策层将非机动车骑行者划分为自由移动、超越等4 种行为。目前电动自行车行为相关研究多聚焦在操作层，缺少对骑行者主动决策行为的分析。同时，多数模型以数值仿真分析为主，仍缺乏有效性验证。

现有基于社会力的电动自行车仿真模型缺乏对实际驾驶过程中复杂决策行为的考虑[10]。鉴于此，本文开展实地观测以收集分析电动自行车骑行轨迹数据，建立基于规则的骑行决策行为模型。然后基于原始社会力，对满足跟随条件、超车条件的电动自行车分别引入跟弛力与超越力，建立基于改进社会力的电动自行车运动仿真模型。同时，考虑3 种不同的超越力设置形式，分析其对电动自行车超越轨迹、速度等的影响规律。

1 数据采集与骑行决策行为模型建立

本文的研究架构如图1所示。首先，开展电动自行车单向流观测实验，考虑骑行微观行为的重要特征参数，利用CART决策树对观测样本进行骑行状态评估，生成电动自行车决策行为规则。然后基于原始社会力，对满足跟随条件、超车条件的电动自行车引入改进行为力，对电动自行车的运动过程进行建模仿真。

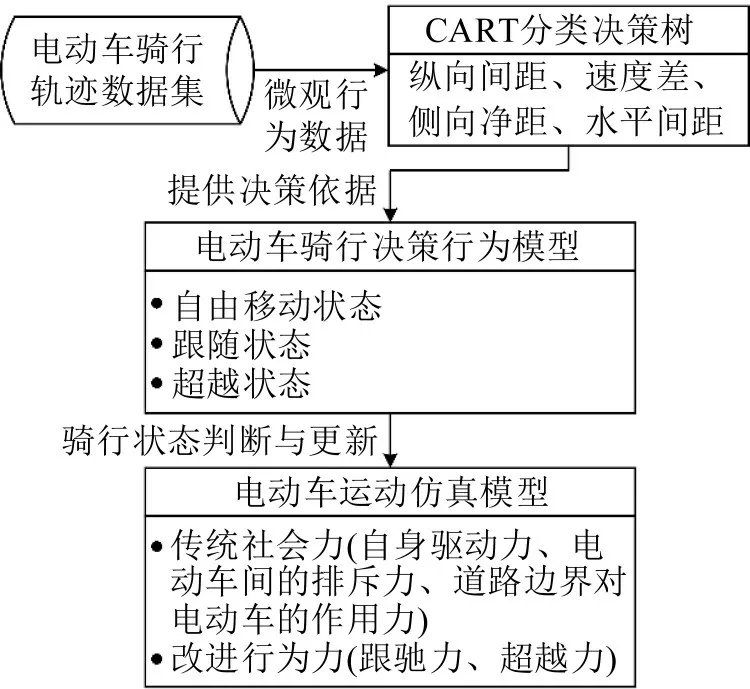
图1 研究架构Fig.1 Research framework

1.1 数据采集

本文数据采集地点为上海海事大学临港校区航务大道，道路取样长度约为60 m，单方向行驶车道宽度为4.75 m，如图2所示。

图2 观测路段及范围Fig.2 Observational section and its range

采用Petrack[11]与Matlab 软件相结合的方式提取电动自行车骑行者轨迹。利用Petrack对骑行者头部进行标定追踪，如图3所示，然后在Matlab 软件中通过直接线性变换方法将图像坐标转换为真实坐标[12-13]。

图3 采用Petrack追踪电动自行车骑行者位置Fig.3 Using Petrack to track position of electric bicycle rider

1.2 基于规则的骑行决策行为模型

以电动自行车在车道上行驶的交通特性指标作为决策参数，对电动自行车在单向流下的自由移动、跟随行为和超越行为规则进行预定义。

1.2.1 CART分类决策树算法

决策树模型通过连续的逻辑判断得到结果，建树主要依据表示系统混乱程度的基尼系数(gini)。基尼系数越高表示系统混乱程度越高，而建立决策树模型的目的就是通过合适的分类来降低系统的混乱程度。基尼基数的计算公式为

式中：C为样本T的类别数；pi为类别i在样本T中出现的频率，即类别为i的样本占总样本个数的比例。

对采集的电动自行车数据进行预处理后，根据现有研究[9,14]对非机动车骑行行为划分的依据，结合观测环境特征，选取纵向距离、侧向净距Dju、速度差vi-vj、横向间距这4 个特征变量，特征变量的定义如图4所示。纵向距离为两电动自行车之间沿平行于边界障碍物的距离，横向间距为两电动自行车沿垂直于边界障碍物的距离，侧向净距Dju为前方电动自行车j与两条道路边界的最大垂直距离，速度差vi-vj为电动自行车i与电动自行车j在平行于道路边界方向上的速度差，将分类目标划分为自由移动、跟随、超越这3类行为状态。

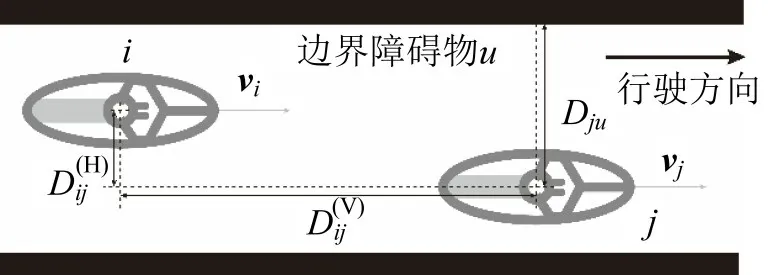
图4 特征变量的定义Fig.4 Definition of characteristic variables

将采集的150条电动自行车轨迹划分为2个集合，其中120 条为训练集，另外30 条为测试集。对模型进行训练及预测，预测结果正确率为90%，同时对影响分类目标的4 种特征变量进行重要性评估，评估结果如表1所示。

表1 不同特征变量的特征重要性Table 1 Characteristic importance of different characteristic variables

由表1可以看出，电动自行车在骑行过程中的行为选择主要受纵向间距影响，影响程度为42.44%，其次分别为速度差27.18%、侧向净距17.00%、横向间距13.37%，决策树可视化如图5所示。从图5可以看出，分类决策树的叶子节点最后的基尼系数都趋近为0，这表明决策树分类效果较好，4 种特征变量的初始分类节点分别是纵向距离为4.35 m、速度差为1.55 m·s-1、横向间距为0.6 m，侧向净距为1.62 m，这与现存的对于非机动车研究基本一致[14-15]，因此本文建立的基于规则的行为选择模型以上述节点为参考依据。

1.2.2 基于规则的行为决策机制

通过获取骑行者的属性、其他骑行者、周围环境等信息，本文建立的骑行决策规则如下：

(1)判断在视角范围内，前后两辆电动自行车的纵向间距是否大于4.35 m。若小于4.35 m，电动自行车不具备超越的纵向间距条件，为跟随或者自由移动状态。

(2)判断前后车速度差是否大于1.55 m·s-1。若速度差大于1.55 m·s-1，且两车纵向间距大于4.35 m，则可能具备超越条件；若速度差小于1.55 m·s-1时，且两车纵向间距大于4.35 m 时为自由移动状态；若速度差大于1.55 m·s-1，但两车纵向间距小于4.35 m，则电动自行车为跟随状态。

(3)判断前车与最远边界的侧向净距是否大于1.62 m。当前车的侧向净距大于1.62 m时，后车超越前车时满足超越空间，在纵向间距、速度差都满足的前提下，电动自行车为超越状态；当前车的侧向净距小于1.62 m且纵向间距大于4.35 m、速度差大于1.55 m·s-1时，电动自行车为跟随状态。

(4)判断电动自行车横向间距是否小于0.6 m，该数值与相关研究中超越时横向间距为0.5 m[15]的结论相近。当纵向间距小于4.35 m、速度差小于1.55 m·s-1时，若横向间距小于0.6 m，电动自行车为跟随状态；若横向间距大于0.6 m，电动自行车为自由移动状态。

根据CART 分类决策结果(图5)构建电动自行车决策行为规则，具体判断流程如图6所示。

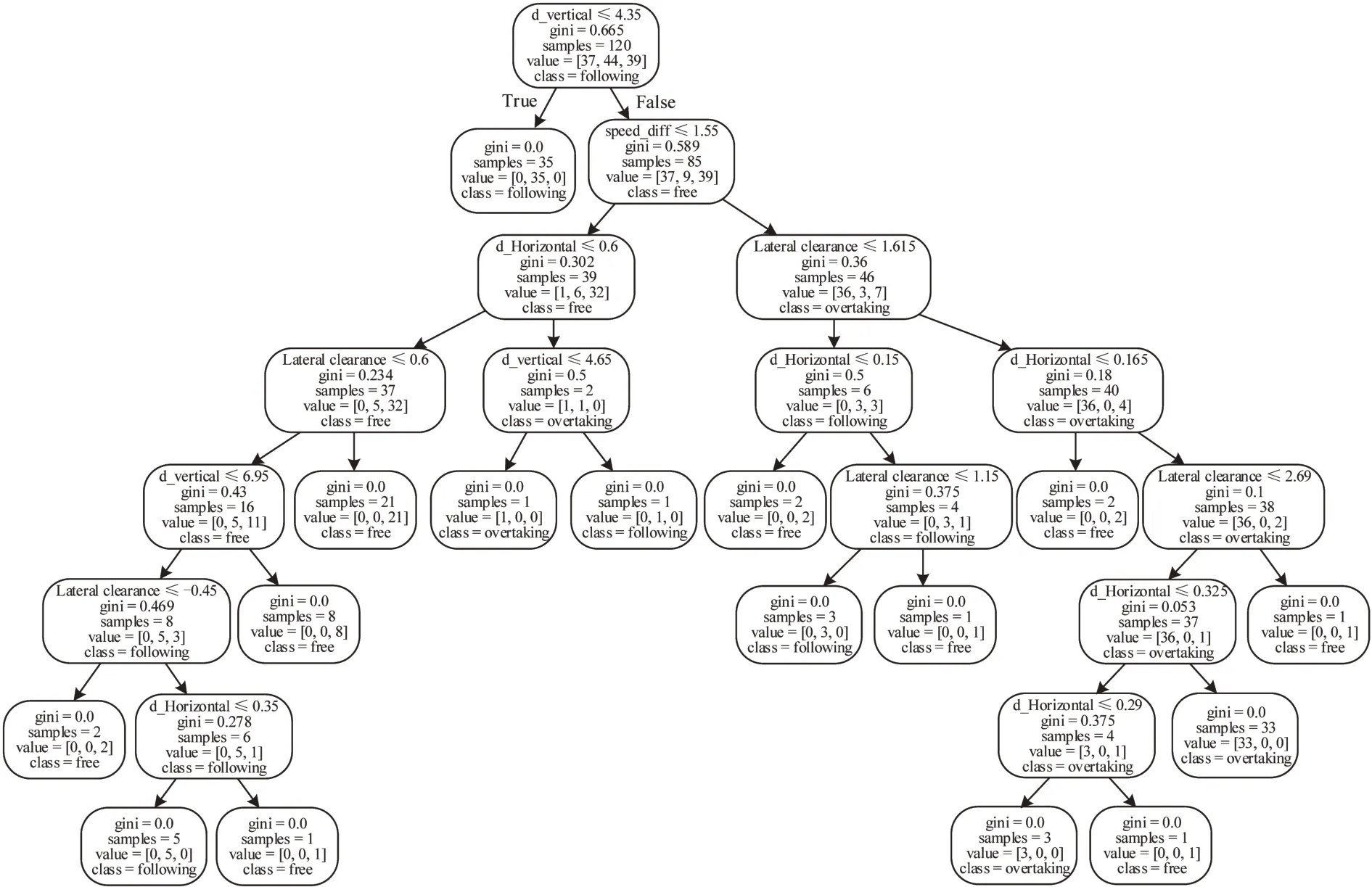
图5 CART决策树可视化效果Fig.5 Visualization of CART decision tree

图6 基于规则的骑行状态判断Fig.6 Driving state judgment based on rules

2 基于改进社会力的骑行仿真模型建立

2.1 传统社会力

基于传统社会力模型，将电动自行车微观行为的内部动机量化为朝期望方向的驱动力、电动自行车之间的排斥力、电动自行车与道路边界的排斥力。由于电动自行车速度过快且机身周围有外凸零件，一旦发生接触极其危险。与行人的传统社会力模型相比，电动自行车社会力模型不引入摩擦力。

2.1.1 自身驱动力

当骑行者的骑行速度vi偏离其期望速度时，骑行者会受自身驱动力的作用，在松弛时间τ内加速达到期望速度，电动自行车骑行者i所受的驱动力为

式中：mi为人与电动自行车总质量，骑行者平均质量为65 kg，新国标中电动自行车标准质量为55 kg，所以mi取值为120 kg；单向流中电动自行车的期望方向设置为当前“车道”方向；τ为松弛时间，取值为0.7 s。

2.1.2 电动自行车之间的排斥力

电动自行车骑行者需要独立的安全空间，骑行者i对于相邻的骑行者j会产生排斥心理，相应的排斥力fij可以用一个随距离递减的指数函数表示，即

式中：Ai为电动自行车之间相互作用的排斥力强度；Bi为电动自行车之间能够产生排斥力的作用距离；nij为由电动自行车j指向电动自行车i的单位向量；Dij为电动自行车i到电动自行车j边缘的距离，即

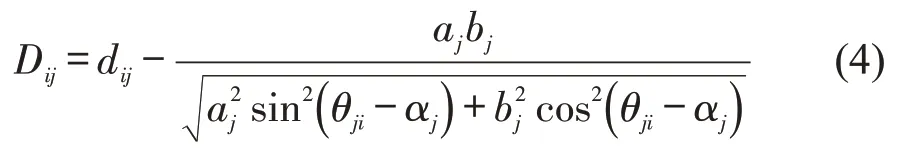
式中：dij为电动自行车i与电动自行车j的中心点连线距离；aj、bj分别为电动自行车j短半轴、长半轴长度；θji为电动自行车i与电动自行车j中心点连线与水平线方向之间的夹角；αj为电动自行车j行驶方向与水平线之间的夹角，具体几何关系如图7所示。

2.1.3 道路边界对电动自行车的作用力

电动自行车在行驶过程中也会受到道路边界的约束，在超车过程中，尤其会注重与道路边界的侧向净距。本文假设，无论电动自行车骑行者从左侧还是右侧超车，仅受最近的单侧道路边界的作用力fiu，即

式中：C为电动自行车与道路边界产生排斥力的作用强度；Diu为电动自行车中心点到边界的垂直距离；Bu为电动自行车能够与道路边界产生排斥力的作用距离；niu为单位向量，由道路边界垂直指向车道内侧。

2.2 改进的行为力

2.2.1 跟驰力

电动自行车在跟随前车时，为了避免碰撞，必须与前车保持一定的安全距离，从而与前车保持相对运动，此时电动自行车骑行者i的安全速度为[16]，为达到安全速度所受的跟驰力fi(att)为

式中：跟驰力fi(att)的方向由电动自行车i指向前车j的车尾中端；a(imax)为电动自行车i的最大加速度，这里取值为1 m·s-2；v(isafe)为由t时刻前车速度vj、当前电动自行车速度vi、两电动自行车间距gi计算，则第i辆车安全跟驰速度为

式中：bi、bj分别为第i和第j辆电动自行车的最大减速度；δi为第i辆电动自行车骑行者的纯反应时间，本文δi取0.3 s。

2.2.2 超越力

首先判断被超越车辆的速度与期望速度的关系，如果被超越车辆的速度大于期望速度，则不再考虑执行超越过程，反之，在满足1.2.2节超越行为规则时，引入超越力。为了比较不同超越力设置形式对电动自行车超车过程产生的实际影响，定义3种超越力。

(1)公式超越力

为了简化模型，Li 等[9]将超越行为按横向与纵向进行解耦，并分别考虑这两个方向上的分力，即

式中：为电动自行车i的超越力；、分别为超越力在横向、纵向上的解耦；yd为电动自行车在超越过程中需要的横向间距，取值为2 m[9]；to为超车时横向偏移的持续时间；t′为横向偏移的开始时间；Δs为当前电动自行车与即将超越的电动自行车的纵向距离，与本文定义的特征变量相同；ex和ey分别是横向、纵向的方向向量。

(2)固定值超越力

多次对比仿真结果与实际轨迹，当仿真步长为0.01 s时，对超越力取固定最优值，即

式中：fi(ovx)为横向超越力；fi(ovy)为纵向超越力。

当满足超越行为规则时触发超越力，当车辆不再满足超越状态条件时，则超越力也解除作用。

(3)目标点超越力

目标点超越力参照文献[6]中超越力的设置形式，引入临时目标点超越向量概念，具体表达式为

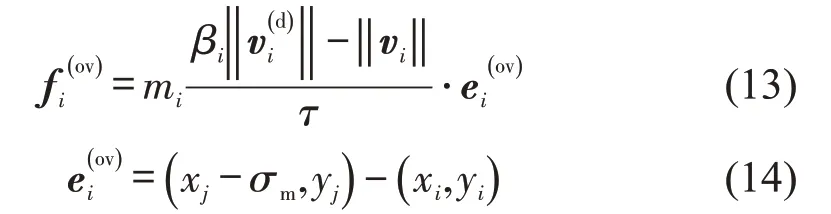
式中：e(iov)为临时目标点超越向量，由超越车辆指向临时目标点方向，具体设置形式如图8所示，其中，βi为超车时期望速度系数，取值为1.2；xi为当前电动自行车横坐标；yi为当前电动自行车纵坐标；xj为前方被超越车辆横坐标；σm为合适超车横向间距；yj为前方确定被超越车辆纵坐标。

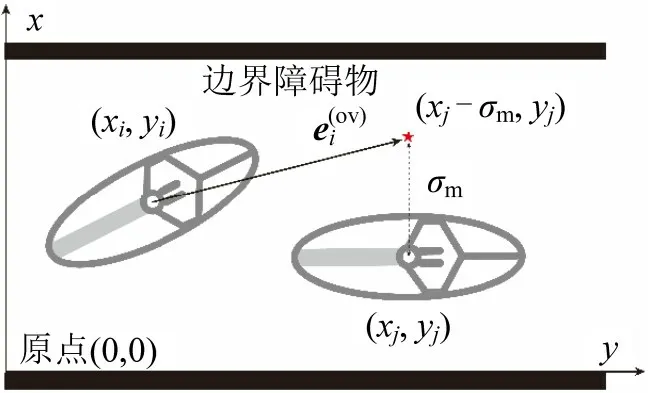
图8 超越向量设置形式Fig.8 Setting of overtaking vector

式中：fi(be)为电动自行车i所受的行为力；fi(att)为电动自行车i处于跟随状态时产生的跟驰力；fi(ov)为电动自行车i在处于超越状态时产生的超越力。

2.3 改进的社会力模型

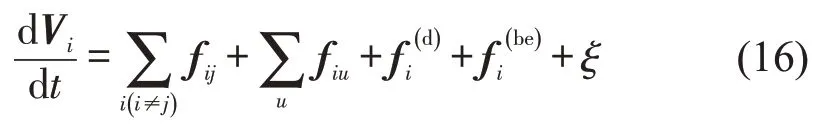
式中：fij为两辆电动自行车之间的排斥力；fiu为边界对电动自行车的边界力；fi(d)为电动自行车自身驱动力；fi(be)为改进的行为力；ξ为随机波动变化。以超越状态为例，受力情况如图9所示。

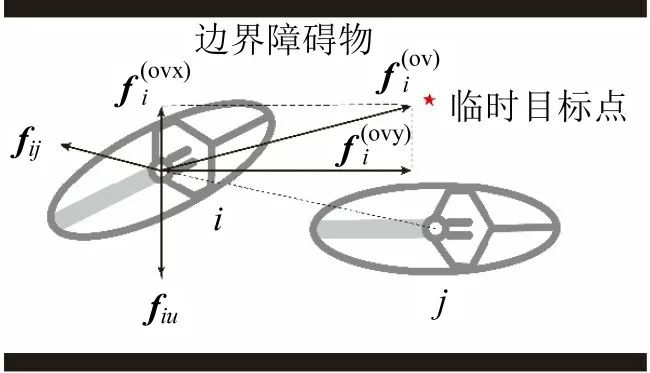
图9 改进社会力模型中超越电动自行车受力图Fig.9 Forces of overtaking electric bicycle in improved social force model

3 仿真实验与结果分析

3.1 仿真环境设置

本文使用Matlab进行仿真，仿真步长为0.01 s。设置车道宽为10 m，长为80 m，初始产生两辆电动自行车，坐标位置分别为(2,0)，(6.5,0)，间隔一段时间在起始线随机位置产生新的电动自行车，在每个时间步判断新产生电动自行车所处的骑行状态，计算赋予改进的行为力，根据新的合力确定电动自行车在下个时间步的位置，仿真环境如图10所示。

图10 MATLAB仿真环境Fig.10 MATLAB simulation environment

3.2 改进社会力模型参数标定

采集数据表明，电动自行车流平均速度为6.6 m·s-1，且速度服从正态分布，如图11所示。

图11 观测数据的电动自行车速度分布Fig.11 Speed distribution of electric bicycle based on observational data

使用采集的数据对本文建立的改进社会力模型进行参数标定。经过多次仿真验证后，社会力模型主要参数值标定结果如表2所示。

表2 社会力模型参数Table 2 Social force model parameters

根据1.2.2 节决策规则可知，当侧向净距大于1.62 m，电动自行车具备超越条件。σm为目标点超越力需要标定的关键参数，考虑安全性与高效性，本文对超车横向间距σm进行分析讨论。

图12表示超车横向间距σm取值为1.5～2.5 m时，处于超越状态的电动自行车超车时间和横向超车速度的变化规律。可以发现，σm的变化趋势与超车时间和横向超车速度变化一致，随着σm的增大，影响程度逐渐增大。

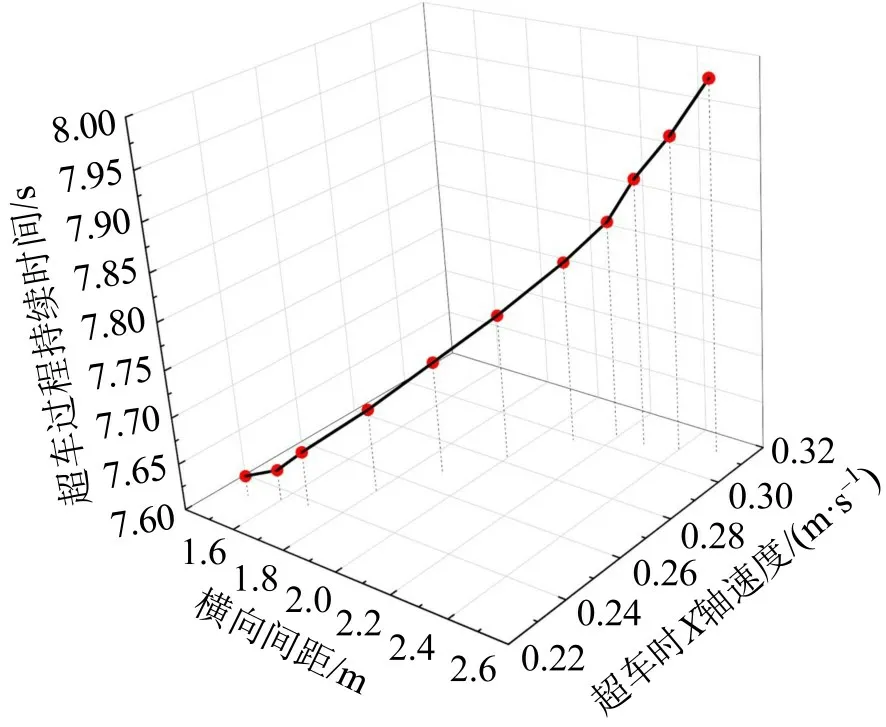
图12 σm 对超越速度和持续时间的影响Fig.12 Influences of σm on overtaking speed and duration

图13表示不同σm对应的超车轨迹，随着σm的增大，超车轨迹会明显左倾，这与实际观测场景一致，但当σm≥2 m 时，由于电动自行车车头横向摆动幅度过大，期望力在摆正行驶方向时会出现轨迹右摆现象，影响了超车效率。因此，本文考虑超车安全性与高效性，将超车时舒适的横向间距设置为2 m。

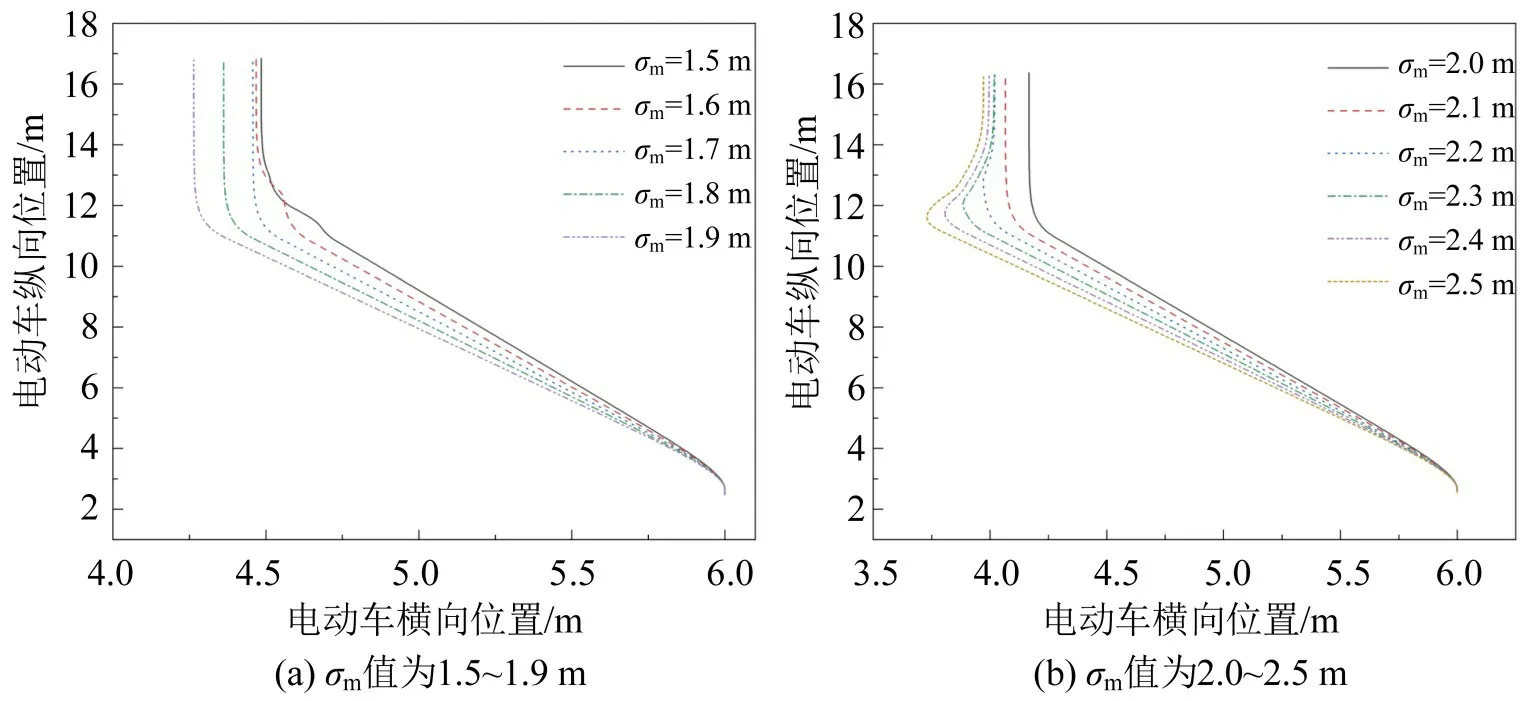
图13 不同σm 值下电动自行车的超车轨迹Fig.13 Overtaking trajectories of electric bicycles in different values of σm

3.3 仿真结果分析

3.3.1 模型轨迹对比不同超越力设置形式对电动自行车超越过程中的轨迹有明显影响，如图14所示。超越时提前作出避免碰撞的行为反应时，轨迹更加流畅和真实。为对比仿真轨迹与实际观测轨迹之间的相似度，提出平均轨迹横向偏移量(AE)作为超车动作完成之前的评价指标，即

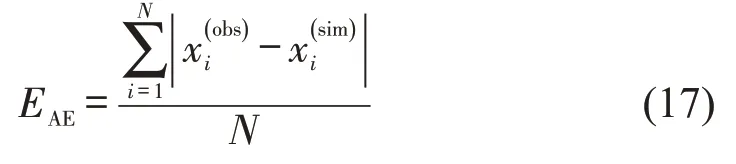
式中：、分别为实际轨迹、仿真轨迹的X轴方向偏移量；N为仿真过程中电动自行车完成超越过程的帧数。

图14中，B曲线为调查数据中电动自行车的实际轨迹，D曲线、F曲线、H曲线和J曲线分别为原始社会力模型与目标点超越力、固定值超越力、公式超越力形式的改进社会力模型的仿真轨迹，其平均轨迹横向偏移量分别为0.157，0.109，0.152，0.327 m。待超车完成时，横向偏移量趋于稳定，D 曲线、F 曲线、H 曲线和J 曲线与B 曲线的横向偏移量分别为0.304，0.090，0.286，0.580 m。目标点超越力的改进社会力模型在超车完成前的平均轨迹横向偏移量和超车完成后的稳定横向偏移量均最小。

图14 不同超越力设置形式对超车轨迹影响Fig.14 Influence of different overtaking force settings on overtaking trajectories

在超越行为初期，电动自行车逐渐调整行驶方向，该阶段轨迹的横向偏移并不明显，随着超越时侧向净距的增大，轨迹的横向偏移也逐步增大并逐渐趋于稳定。在目标点超越力的改进社会力模型中(F曲线)，从轨迹可以看出，电动自行车在纵向距离约5 m 处开始启动超越行为，这与有关学者[17]设置的电动自行车纵向感知域5 m相似，显示骑行者对前方电动自行车采取了提前规避的行为。在固定值超越力的改进社会力模型中(H 曲线)，由于超越力的驱动，虽然电动自行车能够被动提前实现超越行为，但是稳定后横向偏移误差较大。Li 等[9]采用的公式超越力的改进社会力模型(J 曲线)，尽管其能较好地复现在复杂十字路口混合交通流中电动自行车的超越行为，但该模型的仿真轨迹与本文观测的单向通道电动自行车超越轨迹的横向偏移误差较大，这可能与本文观测的单向电动自行车流速度较快有关。

3.3.2 超越车辆速度分析

4种不同超越力设置下，超越车辆横向、纵向速度的变化规律如图15所示。从速度变化趋势可以看出，4种超越力形式下，超越车辆的横向、纵向速度变化趋势基本一致。固定值超越力的改进社会力模型模拟的超越行为持续时间最长，其横向、纵向速度变化更平缓，如图15(c)所示。在公式超越力的改进社会力模型中，超越车辆的速度变化相对较小，如图15(b)所示。而目标点超越力的改进社会力模型模拟的超越行为持续时间最短，因此其横向、纵向速度变化更迅疾，最大横向速度可以达到0.3 m·s-1，如图15(d)所示，且与其他形式超越力不同的是，在横向移动过程中，为了与前车保持最佳的横向间距，超越电动自行车会主动采取加减速行为，如图15(d)所示，图中折线代表加速超越后，其横向速度会减小，在判断横向间距过小时，电动自行车会主动加速以加大横向间距，后至满足超越的安全距离后，横向速度减为0。

图15 不同超越力形式对超车速度的影响Fig.15 Influence of different overtaking force settings on overtaking speeds

4 结论

本文根据调查得到的电动自行车骑行轨迹数据将电动自行车在单向流中的骑行行为分为自由移动、跟随和超越状态，利用CART 分类决策树对收集到的数据集进行训练，确定了纵向间距、速度差、侧向净距、横向间距等特征变量，分析骑行行为的决策机制，建立了基于规则的电动自行车骑行行为模型。基于传统社会力模型，对满足不同行驶状态规则的电动自行车分别引入超越力和跟随力，在MATLAB 中进行单向流电动自行车运动仿真。在改进的社会力模型中，对超越力设置3 种形式，分别为公式超越力、固定值超越力和目标点超越力。针对目标点超越力的改进社会力模型，通过比较超车过程轨迹、横向速度和超车时间与真实行驶数据的误差等，对关键参数——超车横向间距σm进行数值标定。最后，对原始社会力模型、公式超越力的改进社会力模型、固定值超越力的改进社会力模型和目标点超越力的改进社会力模型的仿真结果进行比较分析。

结果表明：(1)与其他超越力形式的改进社会力模型和原始社会力模型相比，目标点超越力的改进社会力模型的仿真结果更接近于实际观测轨迹；(2)最佳超车横向间距为2 m；(3)超车横向间距与横向速度变化、超车持续时间成正比，并随着σm增大，影响程度逐渐增大；(4)超越车辆的横向、纵向速度变化趋势基本一致，目标点超越力的改进社会力模型模拟的超越行为持续时间最短，其横向、纵向速度变化相比其他模型更迅速，超越时最大的横向速度可以达0.3 m·s-1。