无信控人行横道多类型冲突严重程度模型

常玉林，吴照允，孙超，张鹏

(江苏大学，汽车与交通工程学院，江苏镇江 212013）

0 引言

城市道路中无信控人行横道，非机动车和行人过街时会与机动车进行交织，此时，行人和非机动车与车辆互相影响[1]。然而，非机动车和行人的过街速度变化存在不确定性，在交互作用中可能会发生冲突，严重的冲突会造成生命危险。因此，为提高非机动车和行人的过街安全，有效避免交通事故，有必要研究行人-机动车冲突和非机动车-机动车冲突。

无信控人行横道处的交通冲突非常频繁且复杂。以前研究行人和非机动车的交通安全，主要依靠历史碰撞记录[2]，数据存在漏报、缺失以及更新等问题。现在的研究主要以交通冲突严重性为研究对象。例如，ZHENG 等[3]提出一种融合后侵入时间、加速度变化率和转向角速度变化率的综合严重度指标，衡量连续冲突的严重程度，并通过二元Logit模型分析冲突的影响因素，但是，研究场景较为简单，且文献中两种冲突为同类型冲突；彭勇等[4]通过交通调查和数据分析的方法探索人车严重程度的影响因素；张燕等[5]通过采用距离碰撞时间指标和冲突速度指标，提出了新的机-非冲突严重程度分析方法；周竹萍等[6]基于交叉口交通冲突视频数据，运用模糊聚类方法得出交通冲突的严重程度和危险性；LI 等[7]以无信号人行横道人-车冲突为对象，使用入侵后时间、入侵碰撞时间和减速至安全时间，采用支持向量机算法进行测试；KUMAR等[8]使用事故发生时间(TA)和冲突速度(CS)确定冲突的严重程度，并利用广义有序回归模型确定影响人-车冲突严重程度的因素。

最近的研究中，将多个交通冲突指标应用于安全分析已经变的很普遍，但每个指标都有其自身的局限性和适用性。考虑到应用环境以及其他冲突指标在交通事故预测的准确性，往往很难确定哪些冲突指标是合适的[9]；JIANG 等[10]基于传统指标的优点和局限性，提出一种改进的指标，结果表明，改进后的指标更适合交通安全评估。除此之外，在无信控人行横道上，交通冲突的发生受多种因素的影响。以往的研究主要是单次的人-车冲突，即单个行人和单个机动车之间的冲突，并分析人-车冲突的影响因素[11]。然而，很少研究单个行人与多个机动车之间的冲突，以及非机动车与机动车之间的冲突。研究表明，在中国，司机不礼让行人是很常见的，也是发生交通事故的原因之一[12]。因为，机动车不礼让行人会出现下面情形：有的机动车礼让，有的机动车不礼让。对于这种情形，其中一个机动车礼让行人，此时，行人过街；另一个同向行驶的机动车不停车礼让，有可能会与行人发生冲突，甚至碰撞。所以，当某一车道机动车礼让行人停车时，行人可能会与同方向行驶的另一车道的机动车发生冲突，将此冲突称为多重威胁冲突。与之前研究的单次冲突相比，多重威胁冲突的机动车与冲突对象之间存在视野障碍，机动车无法提前知道行人或非机动车的大概走向及位置。当行人或非机动车突然出现时，机动车可能无法做出正确的操作，产生冲突的后果较为严重，甚至发生碰撞。

综上所述，本文引入多重威胁冲突，考虑到多重威胁冲突的差异性，提出冲突时间(TTZ)，再结合后侵入时间(PET)和安全减速度(DST)两个冲突指标，量化交通冲突的严重程度。通过视频数据，分别提取多重威胁冲突和单次冲突的冲突指标值。以两种类型冲突的3类冲突指标值作为基础数据，运用模糊C-均值聚类方法识别严重冲突和非严重冲突。以严重冲突和非严重冲突作为因变量，影响因素为自变量，建立基于二元Logit 模型的多类型交通冲突严重程度预测模型，识别显著影响因素，并使用弹性分析法分析显著影响因素。

1 交通冲突分析及数据调查

1.1 多重威胁冲突

交通冲突指交通行为者在参与道路交通时，两个道路使用者在空间和时间上接近彼此到某种程度，此时，如果两者的运动保持不变，则会导致交通损害危险的发生[13]。所以，将无信控人行横道单次冲突定义为行人或非机动车与机动车在道路交通中，行人、非机动车或机动车感知到危险时，通过改变速度或者采取其他避险措施以避免碰撞的交通遭遇事件。

在无信号人行横道上，当一名司机为行人或非机动车停车让行时，该行人或非机动车可能会与另一车道同向行驶的机动车发生冲突，本文将这种情况称为多重威胁冲突。不同类型的交通冲突如图1所示。

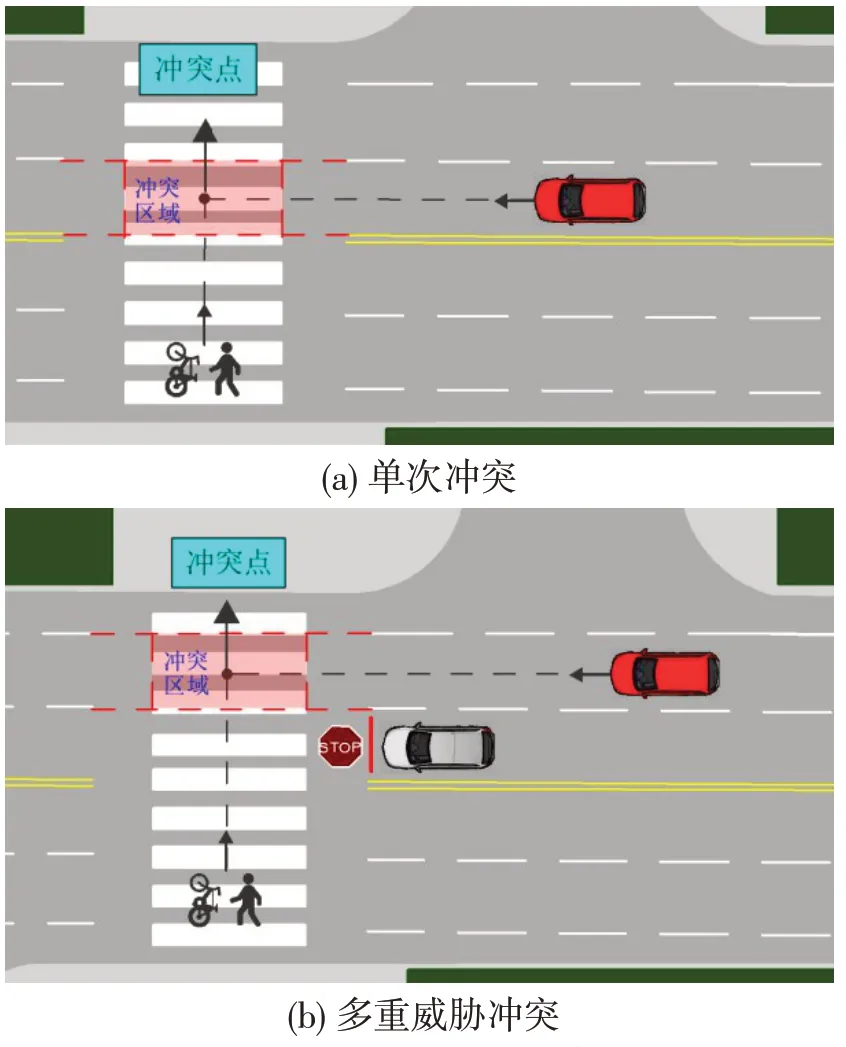
图1 不同类型的交通冲突Fig.1 Different types of traffic conflict

1.2 数据收集

本文运用视频录像观测法获取无信号人行横道交通冲突数据，选取镇江市京口区附近3个无信号人行横道路段，地理位置如图2所示。

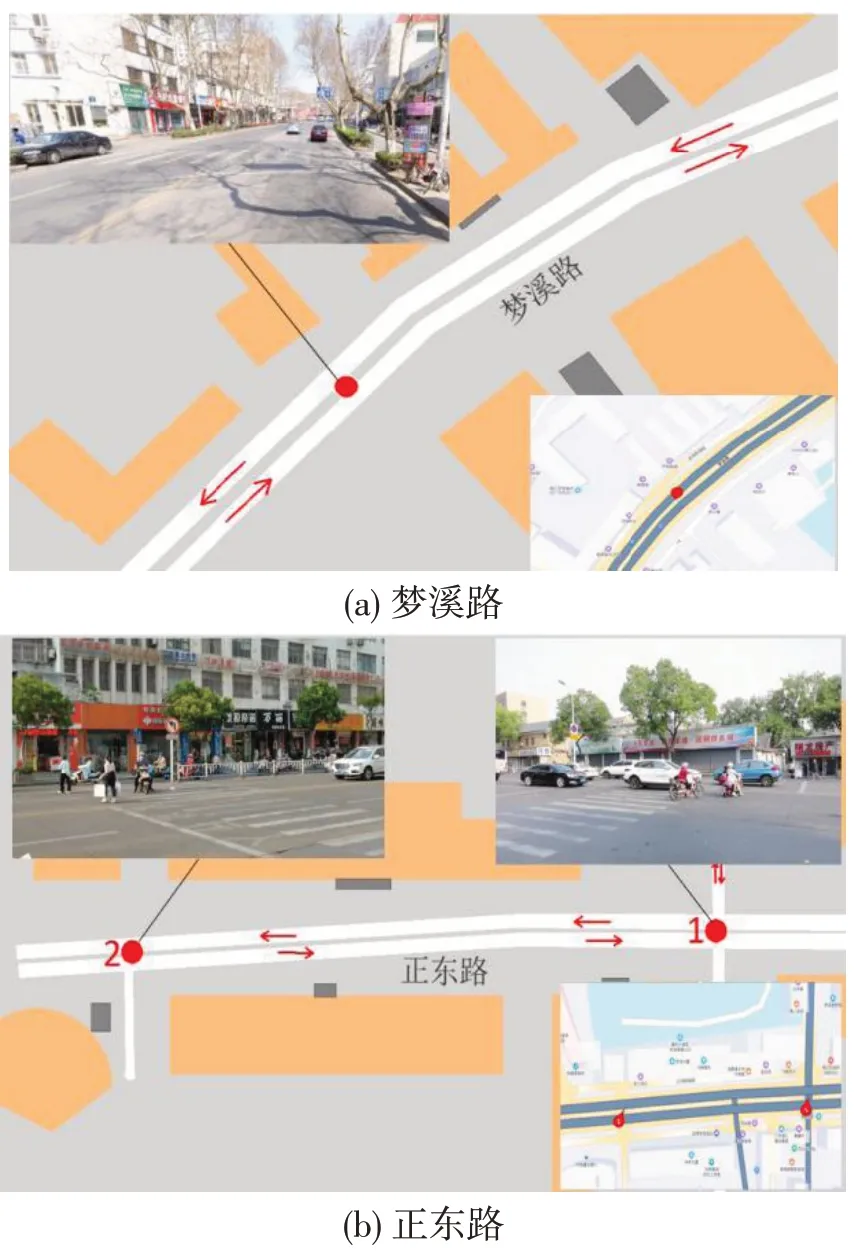
图2 数据采集实地Fig.2 Real map of data acquisition

根据3个地方的交通情况调查发现，存在较大的安全隐患，尤其是机动车不礼让行人或非机动车的情况较为突出，造成大量的交通冲突。每个路段在早晚高峰时连续观测1 h，具体数据如表1所示。

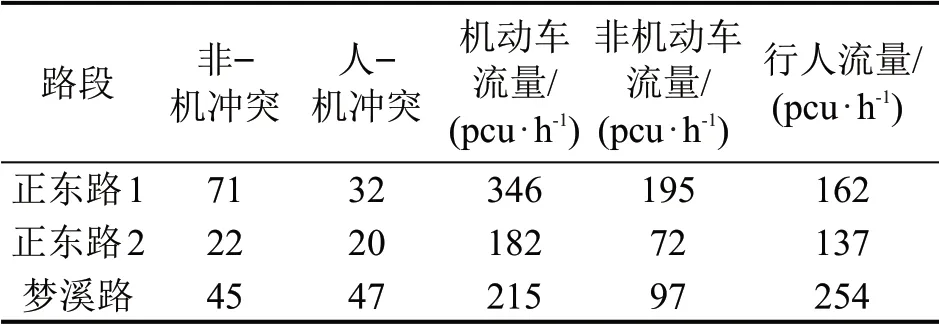
表1 无信控人行横道冲突数据Table 1 Conflicting data of uncontrolled pedestrian crosswalk

由表1可知，无信号人行横道不同，冲突的发生次数不相同，这与人行横道的机动车流量、非机动车流量以及行人流量相关。

1.3 冲突指标设计

为了量化交通冲突，选取相应的交通冲突指标。对于行人或非机动车和机动车之间的冲突，后侵入时间(Post Encroachment Time,PET)被认为是最佳测量方法[14]，因为它可以精确地捕捉每次冲突的靠近程度。安全减速度(Deceleration to Safety Time,DST)可体现出行人和非机动车的加速度变化，表征冲突的严重程度和变化。除此之外，根据多重威胁冲突的实际情况，本文设计了冲突时间TTZ。

(1)PET

PET指第1位道路使用者离开潜在冲突区域到第2位道路使用者到达冲突区域之间的时间，即后侵犯时间。

式中：ZPET为后侵犯时间计算值(s)；T1为非机动车离开冲突区域的时间(s)；T2为车辆到达冲突区域的时间(s)。

(2)DST

本文设安全减速度为DST，研究的冲突对象为行人和非机动车。然而，行人或非机动车在过街时，当意识到有车辆到达，他们会选择合适的时间过街。所以，将行人或非机动车过街分为两阶段计算DST，即

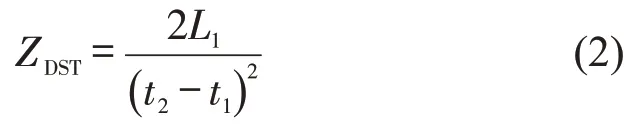
式中：ZDST为安全减速度计算值(m·s-2)；t1为行人或非机动车意识有车辆到达的时间(s)；t2为行人或非机动车到达冲突点的时间(s)；L1为t1到t2之间的距离(m)。

(3)TTZ

后侵入时间是双方通过冲突区域的时间差，在通过冲突区域时，机动车已知行人或非机动车的存在，从而进行加速或减速，而安全减速度不能表征机动车属性。对于多重威胁冲突，机动车和冲突对象之间存在视野障碍，机动车不知道行人或非机动车的存在，在靠近人行横道时速度变化是不确定的。所以，为了更好地表征多重威胁冲突，提出了冲突时间TTZ。

TTZ 为行人或非机动车意识到有机动车到达时，与其发生交通冲突的机动车离人行横道的距离与当前车速的比值。本文采用机动车的接近事件描述冲突，即

式中：ZTTZ为冲突时间计算值(s)；L2为机动车至人行横道前的距离(m)；V为行人或非机动车意识到有机动车到达时，机动车的速度(m·s-1)。

2 基于模糊C-均值的冲突严重程度聚类

2.1 模糊C-均值聚类分析方法

聚类是交通安全的常用研究方法之一。模糊C-均值聚类算法(Fuzzy C-Means,FCM)属于无监督学习算法，该算法具有结构简单、局部搜索能力强且收敛速度快的特点。适用于模糊和无清洗界限的交通冲突严重程度划分，为了融合多个冲突指标确定冲突严重性类型，采用FCM 算法进行研究。选取后侵入时间PET、行人安全减速度DST 和冲突时间TTZ 这3个冲突指标，对冲突严重性进行聚类。其最小化目标函数为

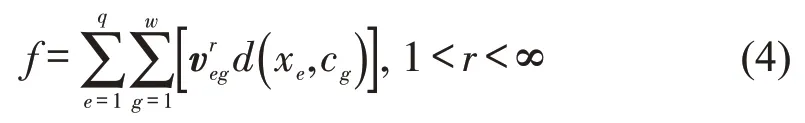
式中：f为模糊聚类的误差平方和；r为模糊指数；q为样本点总数；w为聚类簇的数目；为样本e属于g类簇的隶属度，通常为隶属度矩阵；xe为第e个参与聚类的样本点；cg为g类簇的聚类中心；d(xe,cg)为xe与cg的距离函数。

2.2 冲突严重程度聚类结果

本文基于后侵入时间PET、安全减速度DST及冲突时间TTZ 指标建立冲突样本数据库，通过Matlab 软件分析无信控人行横道的237 个冲突样本，按照FCM 算法流程，设定类中心c=2，聚类结果如图3所示。

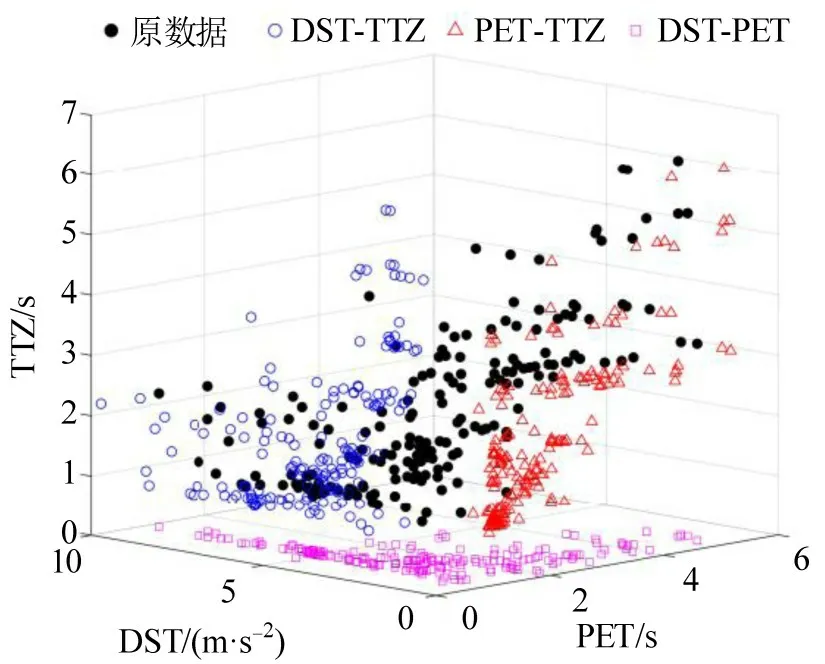
图3 冲突原始数据散点及各平面投影Fig.3 Scattered points of conflicting original data and projection of each plane

根据聚类结果，设置冲突严重等级为严重冲突和非严重冲突。通过算法迭代，得到聚类中心(PET、DST、TTZ)坐标，反映了两个不同冲突等级的指标特征，如表2所示。

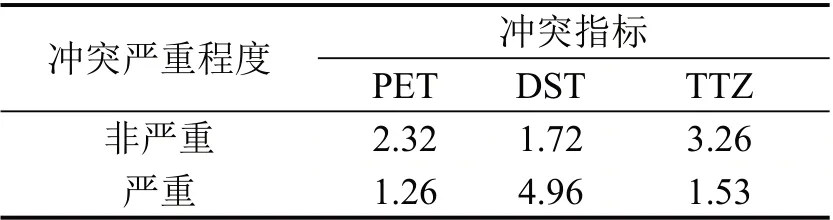
表2 冲突严重程度聚类中心Table 2 Cluster center of conflict severity

严重冲突表示非-车冲突或人-车冲突非常危险，极有可能发生碰撞事故；非严重冲突表示冲突危险系数小。PET 和TTZ 值越低，DST 值越大，发生的冲突越严重。

由图4可以直观地看到，越往左下方，冲突越严重。对于冲突次数来说，单次冲突要多于多重威胁冲突。然而，对于冲突严重性，多重威胁冲突的严重冲突比例比单次冲突大，对行人或非机动车过街安全将会造成更大的威胁。

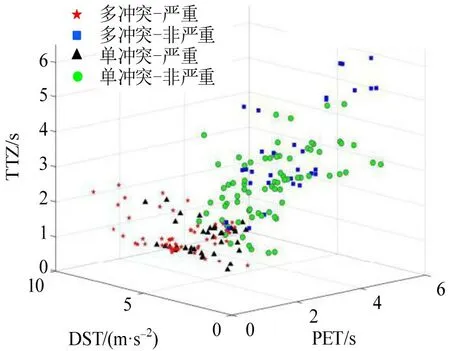
图4 两种类型冲突的严重程度聚类结果Fig.4 Clustering results of severity about two types of conflict

由图5可以直观地看到，非机动车的冲突次数不但比行人多，非机动车的冲突严重程度比例也比行人大。

图5 两种冲突对象的严重程度聚类结果Fig.5 Clustering results of severity about two conflicting objects

传统冲突严重程度是根据冲突指标阈值识别，以后侵入时间PET 为例，通过PET 累积频率的第85%分位数作为区分严重和非严重冲突的截点值，本文PET 的截点值计算为2.75。模糊聚类方法与传统指标阈值方法比较如图6所示。

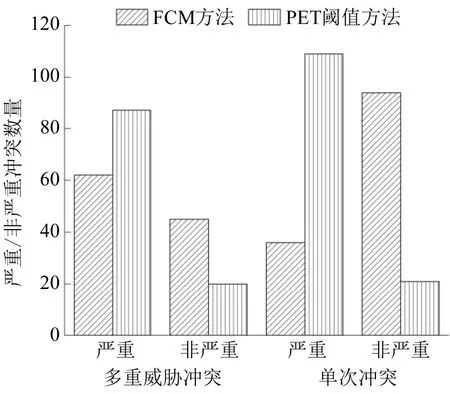
图6 不同方法冲突严重程度的判别结果Fig.6 Distinguished result of different methods for conflict severity

由图6可以看出，与FCM 方法相比，不论多重威胁冲突还是单次冲突，冲突指标阈值识别的严重冲突数量较多。而实际情况并非如此，因为当行人安全通过冲突区域后，机动车可能会加速通过冲突区域，得到的PET值较小，但行人过街是安全的，容易误判为严重冲突，因此，采用冲突指标阈值方法很难准确识别。而模糊聚类方法利用后侵入时间、安全减速度及冲突时间这3 个指标获取冲突严重程度的聚类中心，采用隶属度的大小判定属于哪种冲突(严重或者非严重)，与传统的阈值方法相比，提高了准确性和有效性。

3 冲突严重程度建模与结果分析

通过实地调查和数据分析，提取有关冲突严重程度的影响因素，由上述的聚类结果，将交通冲突分为严重冲突和非严重冲突。以冲突的严重程度为因变量，影响因素为自变量，构建二元Logit 模型，并用贝叶斯估计方法标定模型参数，运用弹性分析讨论显著影响因素。

3.1 侧面车辆礼让停车分析

根据视频数据分析，对于多重威胁冲突的侧面停车分为两种停车情况：(1)侧面车辆直接在礼让线处停车；(2)侧面车辆缓慢行驶越过礼让线，在人行横道上遇到行人或非机动车时停车，如图7所示。

对于上面的两种停车情况，本文重新定义。将在礼让线处直接停车的情况，定义为车辆合法停车行为；对于缓慢行驶越过礼让线停车的情况定义为车辆不合法停车行为。

3.2 影响因素提取

本文选取的影响因素主要包括：是否混合通行，机动车数量，行人和非机动车的过街速度和过街方向，前方车辆屈服行为以及侧面车辆合法停车行为等，具体变量名称及取值如表3所示。变量分为连续变量和分类变量，其中，分类变量取值为1或0，连续变量根据设定属性范围进行取值。

表3 关键变量描述Table 3 Description of key variables

3.3 多类型交通冲突严重程度预测模型

(1)模型建立

根据聚类结果，对于交通冲突，可能是严重的，也可能是非严重的。Logistic回归模型是研究二元关系最有效和广泛使用的方法[15]。假设Y是交通冲突严重性的二元结果，Y=1 表示严重冲突；Y=0表示非严重冲突。对于冲突对象n(n=1，表示行人；n=2，表示非机动车)，在第k种冲突下(k=1，表示多重威胁冲突；k=2，表示单次冲突)的冲突严重程度i(严重或非严重)的随机效用定义为

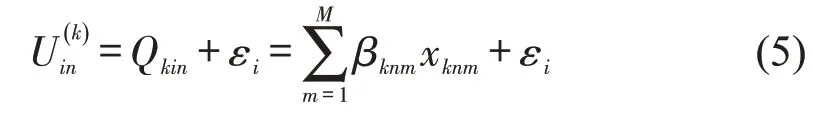
式中：M为解释变量个数；为第k种冲突下，冲突严重程度i的效用；Qkin为可观测的效用部分；βknm为冲突对象n在第k种冲突下，冲突严重程度i第m个解释变量的相应参数；xknm为冲突对象n在第k种冲突下，冲突严重程度i第m个解释变量，εi为随机误差项，假设εi～N(0，σ2ε)为服从均值为0，方差为σ2ε的正态分布。对于第k种冲突下，冲突对象n的冲突严重程度为i的概率为

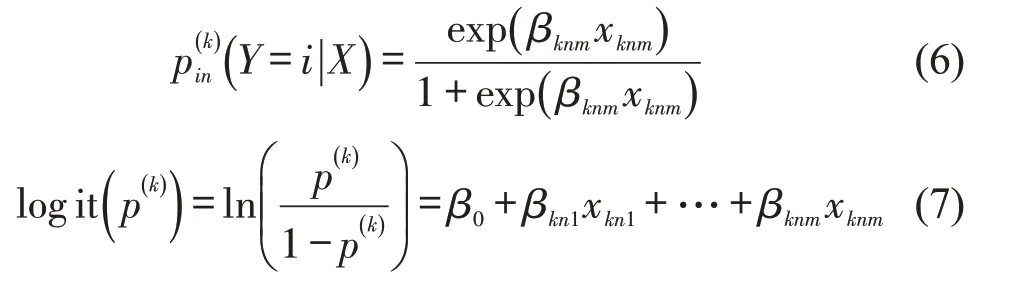
采用偏差信息准则(DIC)比较模型的拟合优度。DIC 结合了模型拟合的度量和对模型复杂性的惩罚[16]为

式中：ZDIC为偏差信息准则计算值；为模型拟合的后验均值偏差；PD为模型中参数的有效个数。一般来说，DIC值越小，模型越好[17]。

(2)弹性分析

为更好地清晰认识解释变量的影响，本文采用弹性分析。弹性可以用变量的1 个单位变化导致结果概率的变化解释，即代表了每个变量对不同类型冲突的严重程度概率的影响。计算式[18]为

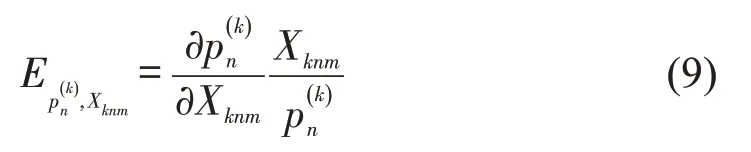
式中：为在第k种冲突下，冲突对象n与机动车之间的冲突概率；Xknm为k种冲突下，冲突对象n的第m个变量。对于二元分类变量，本文采用平均弹性[19]，即

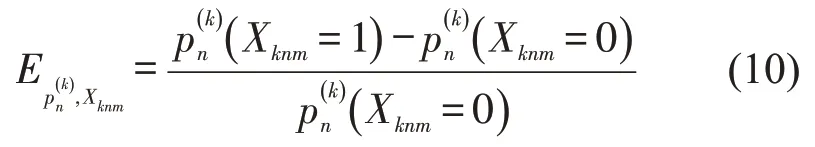
3.4 模型参数估计

本文通过贝叶斯估计方法标定模型的参数。贝叶斯估计方法可以应对更复杂的模型形式，解释数据中存在的不确定性，并产生更准确的模型估计，常采用马尔可夫链蒙特卡罗(Markov Chain Monte Carlo，MCMC)仿真完成参数标定。对于两种冲突，分别设置两个不同初始值的模型参数链，运行50000 次迭代，前20000 次样本丢弃，剩下的30000次迭代用于计算模型估计。模型参数估计结果如表4所示。由表4可以看出，对于行人来说，多重威胁冲突7个变量中有3个变量对模型存在显著影响，分别为等待时间、过街速度以及侧面车辆合法停车行为；单次冲突6 个变量中有3 个变量对模型存在显著影响，其中，等待时间、过街速度以及前面车辆屈服行为这3 个变量均在95%置信区间上显著。对于非机动车来说，多重威胁冲突7个变量中有4 个变量对模型存在显著影响，分别为：机动车数量、等待时间、过街速度以及侧面车辆合法停车行为；单次冲突6 个变量中有4 个变量对模型存在显著影响，其中，等待时间、过街速度以及前面车辆屈服行为这3个变量在95%置信区间上显著，机动车数量在90%置信区间上显著。

表4 模型参数估计结果Table 4 Model parameter estimation results

3.5 结果与讨论

(1)冲突指标分析

本文分析选取的冲突指标PET、DST、TTZ，根据人行横道上的每个冲突事件计算具体数值，冲突指标特征如表5所示。

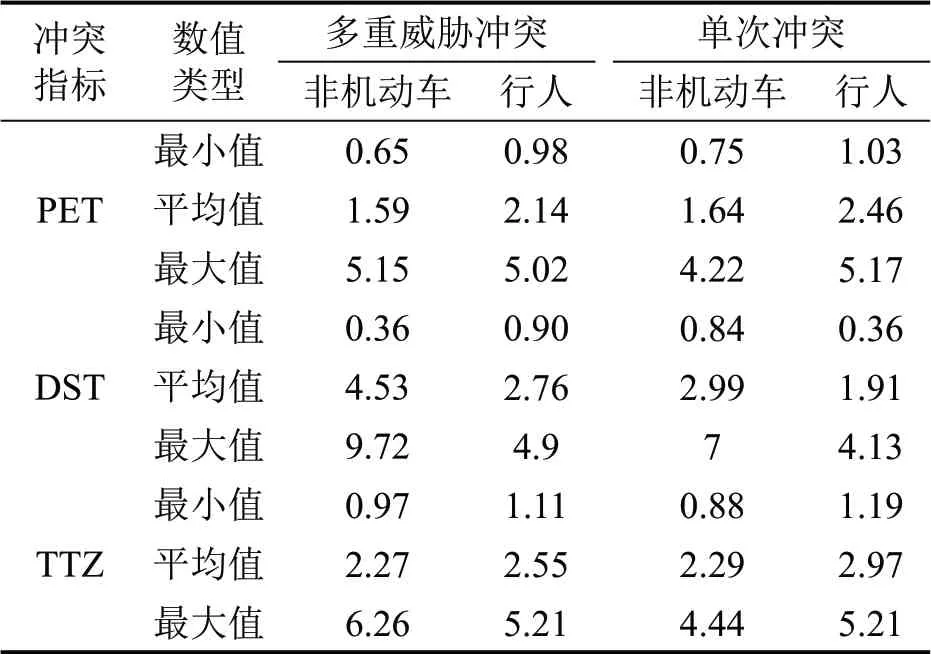
表5 冲突指标数值Table 5 Conflict index value

根据冲突指标定义和特征，PET 和TTZ 值越低，冲突发生概率越高；DST值越大，发生的冲突越严重。

由图8可知，其中“多-非”表示冲突类型为多重威胁冲突，冲突对象为非机动车，其余同理。不论非机动车还是行人，多重威胁冲突的PET和TTZ平均值较低，DST 平均值最高。结果表明，多重威胁冲突下，与机动车之间冲突较为严重。因为在多重威胁冲突情况下，行人和非机动车与机动车存在视野障碍，机动车无法观察到行人和非机动车的移动轨迹，减速靠近人行横道。对于两种类型冲突来说，非机动车的PET 和TTZ 平均值较低，DST 平均值最高。结果表明，两种类型冲突下，非机动车与机动车之间冲突较为严重。因为非机动车速度比行人速度快，过街需要的时间更短，相对于行人来说，非机动车更容易产生侥幸心里，更偏向危险过街。

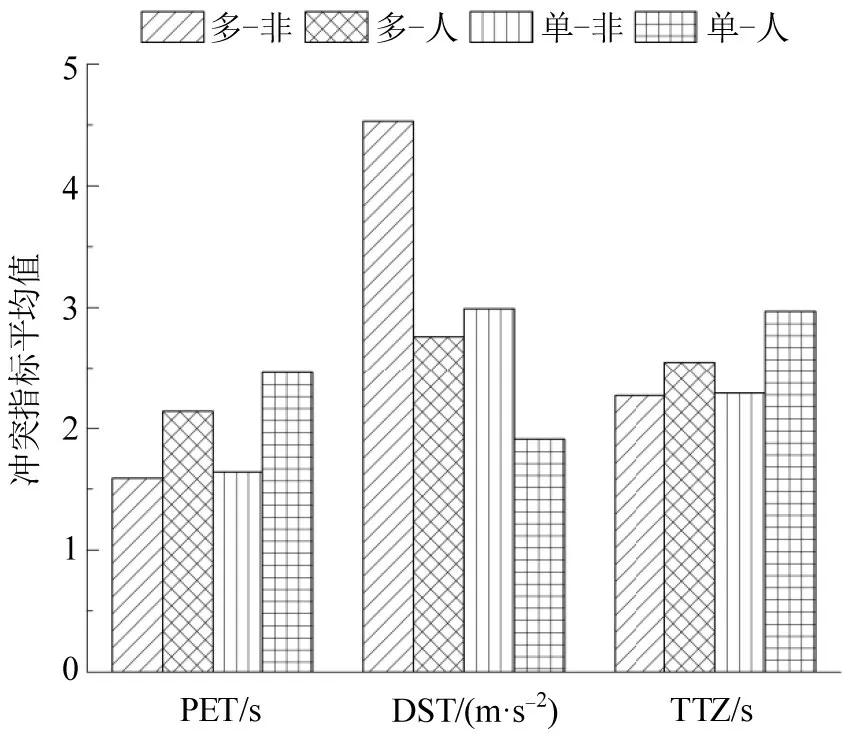
图8 冲突指标平均值Fig.8 Average value of conflict index

(2)显著影响因素弹性分析

对于多重威胁冲突，非机动车与机动车冲突有4 个显著变量，分别是机动车数量、等待时间、过街速度以及侧面车辆合法停车行为；行人与机动车冲突有3 个显著变量，分别为等待时间、过街速度以及侧面车辆合法停车行为。对于单次冲突，非机动车与机动车冲突有4个显著变量，分别是机动车数量、等待时间、过街速度以及前方车辆屈服行为；行人与机动车冲突有3 个显著变量，分别为等待时间、过街速度以及前方车辆屈服行为。这些显著变量的弹性(或平均弹性)如表6所示。

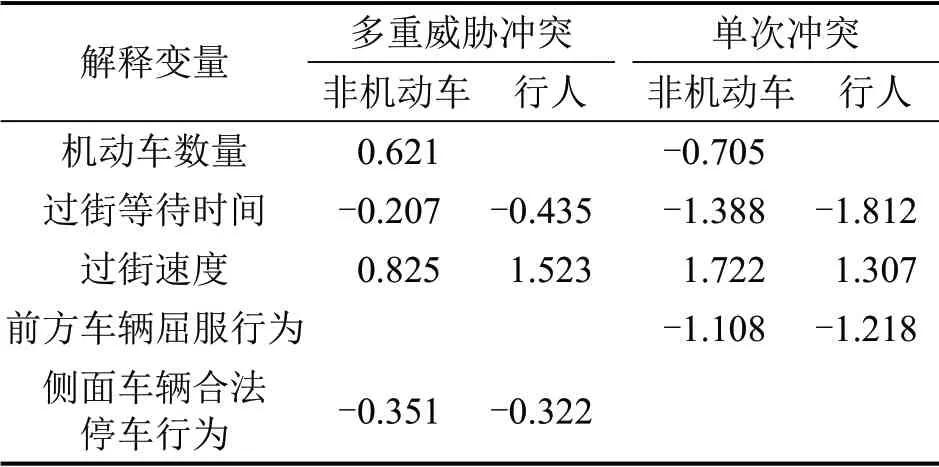
表6 显著变量的弹性(或平均弹性)Table 6 Elasticity(or average elasticity)of significant variables

对机动车数量来说，若机动车数量值增加1时，多重威胁冲突中，非机动车与机动车之间为严重冲突的概率增加了0.62%；单次冲突中，非机动车与机动车之间为严重冲突的概率降低了0.71%。

等待时间也影响不同类型的冲突，若等待时间值增加1 时，在多重威胁冲突情况下，非机动车与机动车之间的冲突属于严重冲突的概率降低了0.21%；行人与机动车之间的冲突属于严重冲突的概率降低了0.44%。在单次冲突情况下，非机动车与机动车之间的冲突属于严重冲突的概率降低了1.39%；行人与机动车之间的冲突属于严重冲突的概率降低了1.81%。

(3)过街速度

非机动车的过街速度对多重威胁冲突和单次冲突的严重程度均显著相关。由图9可知，非严重的多重威胁冲突和单次冲突平均速度较低，分布比较集中；严重的多重威胁冲突和单次冲突平均速度较高，分布比较离散。说明，非机动车过街平均速度较高时，非机动车与机动车更容易发生碰撞且风险高。一方面，较高的非机动车过街平均速度表明非机动车争取尽快通过人行横道，减少等待时间，与机动车争夺路权。尤其在多重威胁冲突情况下，非机动车速度快，反应时间短，碰撞的可能性更高，碰撞后的危险程度也更严重。另一方面，非机动车过街的平均速度是整个过街过程中速度的平均值，较高的车速表示非机动车在过街过程中更多的强行过街行为，意味着更高的冲突严重程度。

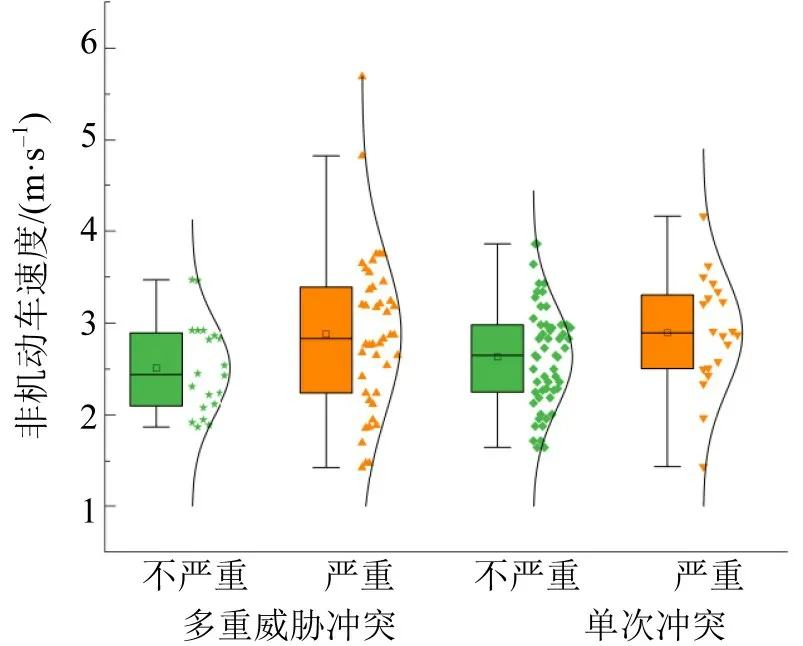
图9 冲突严重程度的非机动车速度分布Fig.9 Speed distribution of non motor vehicle for conflict severity

行人过街速度对多重威胁冲突与单次冲突的严重程度均有正显著影响。因为行人过街速度越快，越容易引起严重的冲突。越快的行人过街速度(例如跑步)，司机的反应时间越短，从而增加严重冲突的概率；反之，行人减速过街会减低严重冲突的概率。这可以解释为减速过街时，行人倾向安全过街，从而降低冲突概率。

(4)车辆屈服行为

前方车辆屈服行为仅对单次冲突严重程度有显著影响，侧面车辆合法停车行为仅对多重威胁冲突严重程度有显著影响，均呈负相关。3 个冲突指标在两种类型冲突不同屈服行为下的分布如图10所示。

由图10可知，前方车辆不屈服行为会增加单次冲突的冲突严重程度；侧面车辆的不合法停车行为会增加多重威胁冲突的冲突严重程度。原因是对于单次冲突，机动车司机可能会下意识地跟随前方车辆，从而忽略行人和非机动车的存在；侧面车辆的不合法停车行为会给旁边车道上的机动车司机一种假象，对于车速较快的机动车，司机分不清侧面车辆是即将停车还是启动行驶，造成机动车匀速驶向人行横道。

图10 车辆屈服行为冲突指标值分布Fig.10 Distribution diagram of conflict index value for vehicle yield behavior

4 结论

本文以后侵入时间(PET)、安全减速度(DST)以及冲突时间(TTZ)这3 个冲突指标作为数据集，运用模糊C-均值聚类方法识别严重冲突和非严重冲突，对比两种冲突的严重程度；以冲突严重程度作为因变量，建立基于二元Logit 模型的多类型交通冲突严重程度预测模型，分析两种冲突严重程度的影响因素。研究结果表明：

(1)行人和非机动车两个冲突对象与机动车之间的冲突严重程度为多重威胁冲突高于单次冲突；对于两种类型的交通冲突，非机动车与机动车之间的冲突严重程度高于行人与机动车之间的冲突严重程度。

(2)关于影响因素，机动车数量(非机动车0.391)、等待时间(行人-0.899，非机动车-0.359)、过街速度(行人2.042，非机动车1.056)和侧面车辆合法停车行为变量(行人-1.394，非机动车-1.653)对多重威胁冲突有显著影响；机动车数量(非机动车-0.365)、等待时间(行人-1.205，非机动车-0.509)、过街速度(行人1.784，非机动车0.890)和前方车辆屈服行为(行人-1.776，非机动车-1.49)变量对单次冲突有显著影响。

本文的研究结果有助于交通管理者采取适当的措施降低无信控人行横道交通冲突的发生率，提高行人和非机动车的过街安全，并为无信控人行横道交通冲突的研究提供新的方向和思路。