基于电子不停车收费数据的山区高速公路车速分布与车型分类研究

徐进，杨子邈，陈钦，陈正委

(重庆交通大学，a.交通运输学院；b.山区复杂道路环境“人车路”协同与安全重庆重点实验室，重庆 400074）

0 引言

近年来，高速公路货车重型化和轿车大型化趋势越来越明显，但汽车性能的迭代速度却远滞后于这种趋势。山区高速公路因地貌条件限制，驾驶环境复杂多变，常见连续弯道、长大纵坡及线形组合不良等高风险路段。不同车型对线形的适应性存在差异，尤其是重型化趋势下货车在长大纵坡的双向均表现出明显的性能衰减，车路协同矛盾导致山区高速公路事故频发[1]。与此同时，车型分类作为交通理论研究，道路线形设计以及速度管理方法制定的基础，面对当前山区高速公路交通组成的新变化，有必要对不同车型的速度特征以及车型分类展开研究。

行驶速度是决定道路安全的重要因素，也是控制道路几何线形和道路交安设施的核心指标，因此，一直是国内外学者研究的焦点，例如，LAN等[2]研究了大型卡车在山区公路不同坡度的速度特征，提出定义明确的卡车速度模型确定临界坡长；YUE等[3]在分析大小型车辆行驶速度稳定性的基础上，建立了陡坡和急弯组合路段的优化设计方法；徐进等[4]提出一种关于重载汽车在弯坡组合路段运行速度建模的新思路，在实现任意坡道位置速度预测的同时，用于确定临界坡长和道路评价；束海波等[5]测试了6 轴半挂式货车以不同入坡初速度驶入上坡的行驶特性，并分析其追尾事故的特征；许甜等[6]根据大小型车运行速度的分布特征、协调性以及一致性等，提出山区高速公路纵坡设计优化方法。除了分析速度与线形之间的关系外，众多学者也从车辆速度预测方面开展研究，例如，DONNELL等[7]在考虑平曲线和纵坡等参数影响下，建立双车道公路卡车速度预测模型；MORRIS 等[8]针对乘用车和卡车开发了多车道公路弯坡组合路段速度预测模型；孟祥海等[9]分析了小客车和大货车运行速度与曲线半径和纵坡之间的关系，建立用于预测平纵组合段运行速度的3种模型。

目前，多从车辆的轴距、比功率及载质量等方面对车型进行分类，例如，侯树展等[10]以轴距作为划分依据，将高速公路的车型划分小车、中车及大车这3 类；马捷等[11]基于车辆比功率等动力性能提出一种在客货分离道路系统中的车型分类标准。但基于山区高速公路车辆实际行驶速度的车型分类方法还比较少，ETC 数据作为一种新的数据来源，具有车型覆盖全面，记录连续及数据量大等优点，能够反映道路上车辆最真实的运行状态，国内外学者鲜有利用高速公路ETC 数据进行速度特征研究。

为此，本文通过采集重庆市包茂高速某段的ETC数据，分析山区高速公路典型路段不同车型的速度特征，运用k-medoids 聚类算法对山区高速一般路段和连续上坡路段车型进行聚类分析，提出基于ETC数据的车型分类方法，分类结果能够为山区高速公路安全研究、线形设计及速度管理等方面提供数据支持和理论依据。

1 数据采集及预处理

1.1 道路技术条件

数据采集道路为包茂高速水江-南彭段，路段为沥青铺装双向4车道高速公路，路面净宽24.5 m，即3.00+7.50+0.75+2.00+0.75+7.50+3.00，设计速度100 km·h-1，于2007年11月28日建成通车，全路段共有3 座隧道、6处立交互通以及1处服务区，本文研究路段为南川-水江段和接龙-石龙段主线道路，如图1所示。路段几何要素如图2所示。

图1 道路平面线位图Fig.1 Bitmap of road plane line

南川-水江段为平缓路段，全长21.60 km，有19处平曲线，其中，半径值1000～2000 m 的平曲线有13 处，2000～4000 m 的平曲线有4 处，4000 m 半径以上的有2 处；纵断面主要变化特征为上下坡交替，坡度值在-4%～3.5%之间，部分路段出现短距离连续上下坡，如图2(a)所示。接龙-石龙段为连续上坡路段，全长12.82 km，有8处平曲线，其中，半径值在2000 m 以下有7 处，2000 m 以上有1 处；纵断面变化特征为连续上坡，坡度值在-0.3%～4%之间，同时，路段内有两处隧道，隧道占比约33%，如图2(b)所示。

图2 路段几何要素示意图Fig.2 Schematic diagram of geometric elements of road section

1.2 数据采集

研究数据来源于高速公路电子不停车收费系统(ETC 收费系统)，系统主要通过安装在公路主线上的ETC 门架采集通行车辆信息。从重庆市高速集团ETC 收费系统后台终端采集包茂高速南川-水江段与接龙-石龙段出城方向ETC门架数据，样本采集时段为2020年7～8月。获取的ETC 门架原始数据按照1辆车1条信息记录在Excel表中，数据信息包含：门架编号、车牌号+颜色、交易时间、金额及计费车型等，其中通行介质OBU 为车载单元，CPC卡为手持车辆通行卡。ETC收费系统中，车型主要分为客车和货车两类，其中，根据车辆轴数、载客数以及载质量分别将客车划分为一型～四型，货车划分为一型～六型，部分车型如图3所示。部分ETC门架原始数据字段如表1所示。

表1 部分ETC原始数据字段Table 1 Partial ETC raw data fields

图3 ETC门架和部分车型示意图Fig.3 Schematic diagram of ETC gantry and some vehicle types

1.3 数据预处理

ETC 原始数据因为复杂环境和机器记录等方面的影响，存在一些无意义的错误数据，该类数据将影响速度特征分析结果的准确性，预处理是通过筛除和清理等方式提高数据质量[12]。

本文主要研究天气晴朗，路面条件良好，车流处于自由流状态下的速度特征，数据提取时段为8:00-18:00，南川-水江段提取有效数据21 d，接龙-石龙段提取有效数据13 d，最小采集样本量为379 个，能够反映车辆实际运行情况。筛除的数据主要为：短时内车牌在同一个门架连续出现2次及以上的数据；前一门架交易时间晚于后一门架交易时间的数据；车型无法识别的数据；速度异常的数据。其中，异常速度数据主要分为两类，第一类是异常低的速度值(研究路段未设服务区)；第二类是超过车辆极限性能的高速值。

速度计算通过比对相邻门架记录的车牌，获取车辆在相邻门架的出入时间，查阅ETC门架运营里程桩号，计算门架之间的里程，行驶里程与行驶时间的比值即为车辆的行驶速度。一天24 h 换算成以秒为单位，即为86400 s，将ETC门架原始时间格式转换为以秒为单位的数值格式后相减得到车辆的行驶时间。

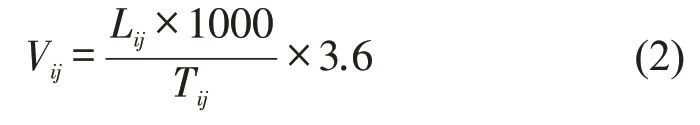
式中：Tij为通过i门架与j门架的时间差(s)；ti和tj分别为车辆通过ETC门架的时刻；Vij为i门架与j门架之间的行驶速度(km·h-1)；Lij为i门架与j门架之间的里程(km)。

2 行驶速度统计分布特征

高速公路行驶速度存在不确定性和随机性，行驶速度受路段线形条件和驾驶环境等因素影响会产生不同程度的差异；另外，不同驾驶人员的驾驶年龄、驾驶风格以及驾驶技能存在差异。统计学原理表明，在基于大量统计数据的分析下，随机现象会呈现出一定的规律性，通过研究山区高速公路大样本ETC行车数据，可以总结不同车型的速度分布特征。

2.1 行驶速度分布

将路段不同车型的行驶速度数据从小到大进行排序，按3 km·h-1间隔进行频数统计，得到不同路段速度频数分布直方图，部分车型速度频数分布如图4和图5所示。

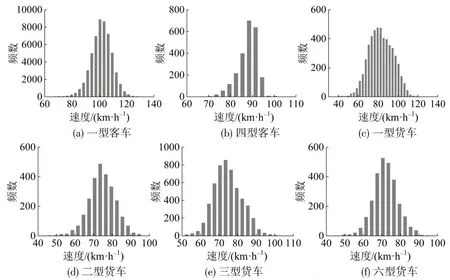
图4 南川-水江段(平缓路段)车型速度分布直方图Fig.4 Speed distribution histogram of vehicles in Nanchuan-Shuijiang section(gentlesection)

图5 接龙-石龙段(连续上坡路段)车型速度分布直方图Fig.5 Speed distribution histogram of vehicles in Jielong-Shilong section(continuous uphill section)

可以看到其中部分车型的速度分布有明显的特点，主要发现如下：

(1)一型客车速度分布在南川-水江段近似正态分布，在接龙-石龙段为负偏态分布，产生该现象的原因是接龙-石龙段道路线形为连续上坡，其中，33%的路段为隧道，一型客车的行车速度受其他车型的车流速度限制，低速行驶的车辆数明显增多。

(2)从图4(b)中可以看到，四型客车速度分布较为集中于最大速度，速度值约为92 km·h-1，超过92 km·h-1的频数显著减少，四型客车为40 座以上营运大巴车，由于营运车辆限速存在，使较少四型客车会超过限速值，而表现为集中于某个最大速度值。图5(b)中，四型客车速度未超过营运限速，速度分布没有表现出明显的集中性。

(3)从图5(d)可以看到，三型货车速度分布呈驼峰状，频数分别在51 km·h-1和68 km·h-1附近达到最大，三型货车是城市近郊货运的主要车型，空载车辆占比较高，其空载与满载工况下爬坡性能差异较大[13]，因此，与平缓路段不同，连续上坡路段三型货车速度分布会出现两个峰值点。

为便于对比分析不同车型速度分布特征，整理不同车型的速度频数数据，绘制相对频率直方图并利用Origin软件中高斯分布进行单峰或双峰拟合，全部车型拟合的R2均大于0.9，拟合效果是较为可靠的，部分车型拟合效果如图6所示。将不同车型的速度相对频率拟合曲线整理如图7所示。

图6 部分车型速度相对频率拟合图Fig.6 Fitting diagram of speed relative frequency of some models

图7(a)和图7(b)是全部车型的频率曲线图，可以看到各车型的速度分布曲线在南川-水江段总体上呈“山”字型分布，而在接龙-石龙段则呈“M”型分布，说明在平缓路段与连续上坡路段不同车型的速度分布有明显差异。

图7 不同车型行驶速度相对频率分布图Fig.7 Relative frequency distribution diagram of driving speed of different vehicles

从图7(c)和图7(d)中可以看到，在平缓路段一型客车和其他3型客车速度分布是错峰的，峰值差最大为14.9 km·h-1；在连续上坡路段4 类客车速度分布峰值相近，峰值差最大为5.9 km·h-1，相比一般路段减小了9 km·h-1。

从图7(e)和图7(f)中可知，在平缓路段一型货车速度分布峰值大于其他5 类货车车型，二型～六型货车速度分布峰值相近；在连续上坡路段不同货车车型的速度分布呈现出较明显的阶梯化差异，其中，三型货车(空载)速度分布峰值最大，六型货车峰值最低。

以上表明，道路线形和车辆性能对速度分布有强烈影响，客车车型速度分布在平缓路段表现为分散，在连续上坡路段则相对集中；货车速度分布变化趋势正好相反，在一般路段集中，在连续上坡路段分散。

2.2 行驶速度特征值

绘制各车型的行驶速度累计频率曲线如图8所示。

图8 不同车型行驶速度累计频率分布图Fig.8 Cumulative frequency distribution diagram of driving speed of different vehicles

从图8(a)和图8(b)中可以看到，对比平缓路段，在连续上坡路段一型客车与其他3 型客车的速度差异显著减小，进一步说明在连续上坡路段一型客车的速度受到较强的限制；二型客车在低速和高速部分占比较高，二型客车是8～19座中型巴士，含营运和非营运两类，个体驾驶员驾驶技能和驾驶风格的差异是造成该现象的主要原因。从图8(c)和图8(d)可以看到，部分货车车型间的频率曲线几乎是重合的，说明部分车型的运行特征有很强的相似性，连续上坡路段车型大致可以分为3类，第1类是一型货车和三型货车，第2类是二型货车和四型货车，第3类是五型货车和六型货车。

在累计频率曲线数据的基础上提取路段不同车型的速度特征值，如表2所示。

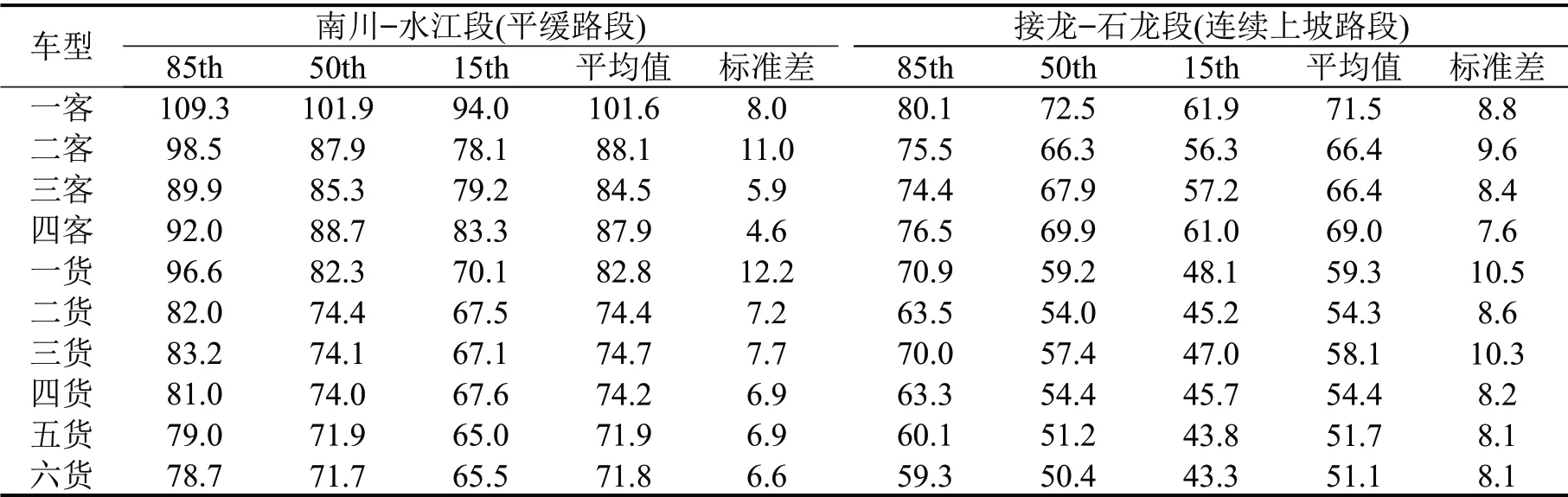
表2 不同车型速度特征值Table 2 Speed eigenvalues of different vehicles

表2中的数值可以为山区高速公路速度管理中限速值的确定提供参考，也能为道路线形设计中不同车型速度阈值的选择提供数据支撑。

从表2中可以看到，连续上坡路段各车型的速度特征值明显下降，但同路段部分车型间多个速度特征值仍较为接近，特别是各车型的速度平均值和标准差并非是连续值，而是呈现一定的聚集性，可考虑作为车型分类的指标。车速标准差也常用于描述速度的离散性，速度离散性越大，车辆间的纵向干扰越严重，连续上坡路段速度离散性总体上要大于平缓路段，路段发生追尾事故的风险水平更高。

3 车型聚类分析

由速度统计分布特征的分析发现，不同线形路段各车型的速度特征并不是按ETC 系统中的车型分类而规律变化，各车型间的速度特征具有一定的差异性和聚集性。基于此，从速度特征值分析中选择分类指标，利用现代统计学的聚类分析方法对不同车型进行聚类分析，实现基于速度特征的车型再分类。

3.1 k-medoids聚类

k-medoids聚类是基于划分的一种快速聚类算法，通过选取原有样本中的样本点作为簇中心点，计算其他样本点与簇中心点的距离进行簇的划分，簇中心点的选择方式使k-medoids 相比k-means 对噪音和孤立点有更强的鲁棒性[14]。k-medoids 通常使用距离度量相似性，目前，常用距离度量有欧式距离、曼哈顿距离、切比雪夫距离和明可夫斯基距离等，本文采用曼哈顿距离进行相似判断，算法通过不断迭代各簇内距离和，当各簇内距离和最小时得到最终聚类结果。

式中：d为样本点间的曼哈顿距离；(xm,ym)和(xn,yn)为样本点；E为各簇内距离的和，当E=Emin时得到最终结果；k为聚类簇的个数；Cl为第l个簇；(xc,l,yc,l)为第l个簇的簇中心点。

3.2 数据准备

相关研究表明，在晴朗白天自由流状态下，速度的标准差趋于稳定，平均速度轻微下降[15]。不同车型的速度平均值和标准差并非一个连续值，而是呈现一定的聚集性，两类特征值能很好地反应车辆本身的运行特性，因此，选取这两类值作为分析样本的聚类指标。南川-水江段全车型10 d交通量组成如图9所示。

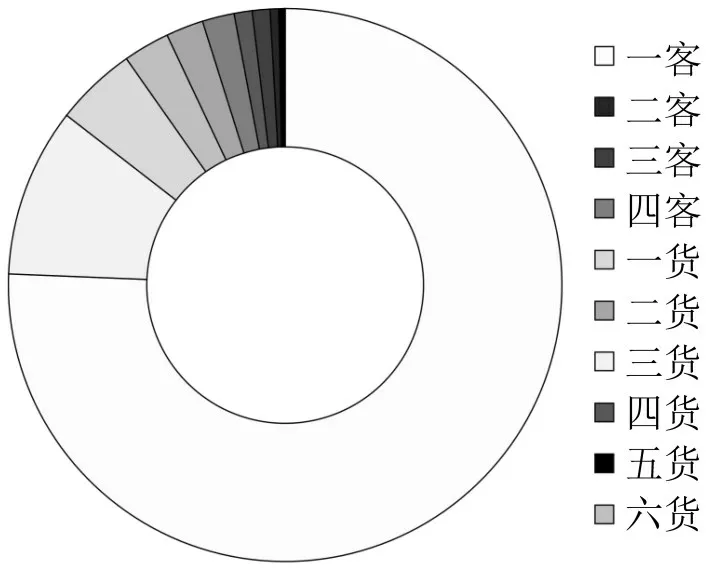
图9 南川-水江段交通量组成Fig.9 Traffic composition of Nanchuan-Shuijiang section

由图9可以看到，高速公路不同车型交通量有显著差异，为保证单个步长内和最终抽取样本点的数量，动态选择不同车型的分组步长，同时，考虑到二型客车和五型货车在样本采集数量中占比仅为0.49%和0.38%，因此，在聚类中暂不考虑这两类车型。

将同一车型行驶速度数据按照采集时序进行排列并编号(1 ～N)，然后，设定分组步长L进行统计分组，即取l1=1 ～L，l2=L+1 ～2L，l3=2L+1 ～3L,…,直至n=N L为止，分组后计算组内的聚类指标用于聚类，不同路段抽样分组结果如表3所示。

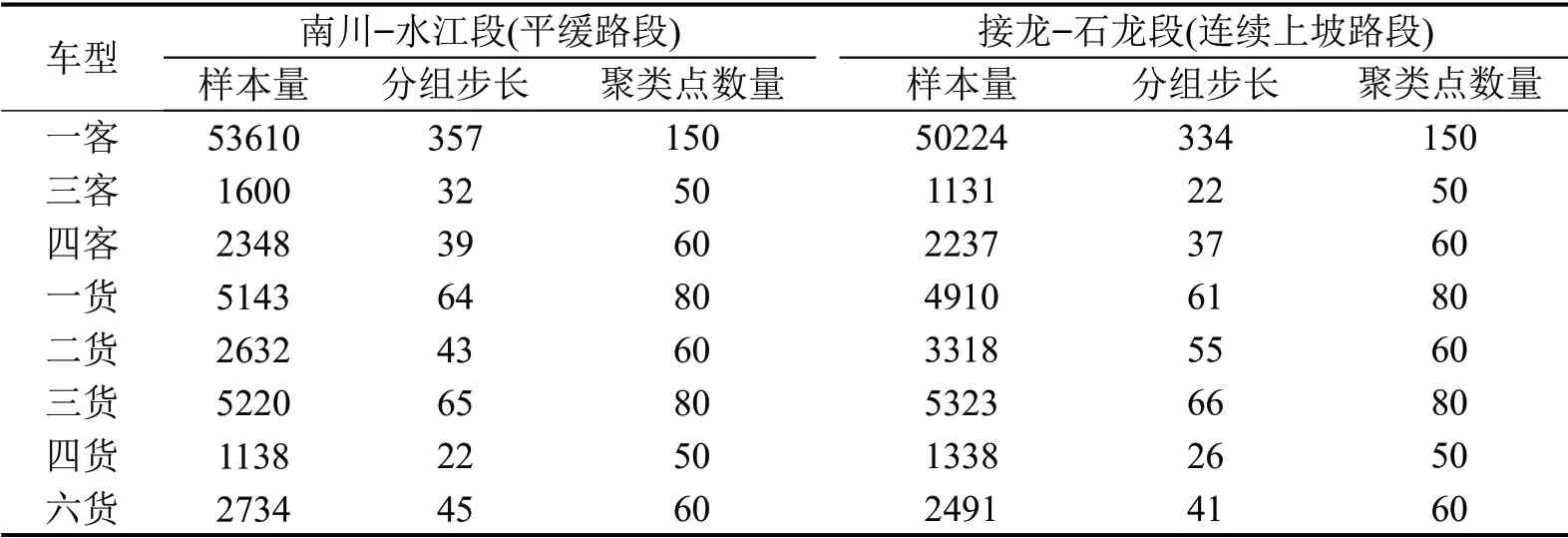
表3 不同路段抽样分组结果Table 3 Sampling and grouping results of different section

3.3 聚类实现

根据分析，初始聚类k值定为2～4，利用Matlab软件进行聚类，对比聚类结果发现南川-水江段和石龙-接龙段分别在k=4 和k=3 获得较理想的效果，如图10所示。

图10 不同车型最终聚类结果Fig.10 Final clustering results of different vehicles

可以看到，平缓路段各车型聚类点较分散，按指标能够聚成4类；连续上坡路段各车型聚类点分布相对集中，但总体上能够聚成3 类，其中，类别2和类别3都包含较多数量的三型货车聚类点，这可能与三型货车的工况有关，空载三型货车行驶速度更快，速度离散性相对较大，与一型货车有较强的相似性，而满载工况下则与二型、四型及六型货车相似，车型聚类统计结果如表4和表5所示。

从表4和表5中可以看到，不同路段聚类后各类别的簇中心点数值，对比表2中各车型样本总体的速度平均值和标准差发现，聚类结果的簇中心点能够较好地与之对应。

表4 南川-水江段(平缓路段)聚类结果统计表Table 4 Statistical table of clustering results of Nanchuan-Shuijiang section(gentle section)

表5 接龙-石龙段(连续上坡路段)聚类结果统计表Table 5 Statistical table of clustering results of Jielong-Shilong section(continuous uphill section)

基于车型聚类的结果，结合不同车型的速度分布特征对车型分类表进行优化。二型客车的速度特征与三型和四型客车相似，因此，二型客车在平缓路段和连续上坡路段分别归为类别2 和类别1；在速度累计频率曲线的分析中，连续上坡路段货车车型能够分为3类，据此将表4聚类结果中的类别3进一步划分为两类，其中，五型货车与六型货车归为一类，优化后的车型分类结果如表6所示。同时，在综合车辆速度特征、交通量组成以及车辆动力等因素，在每一分类中给出了1～2种代表车型。

表6 优化后车型分类表Table 6 Optimized vehicle classification table

4 结论

利用重庆市包茂高速某段ETC数据，分析了山区高速公路不同车型在平缓路段和连续上坡路段的速度分布特征，结合k-medoids 聚类算法对不同路段的车型进行聚类分析，得到主要结论如下。

(1)在不同线形路段上部分车型的速度分布有明显的特点，其中，最显著的是三型货车在连续上坡路段速度分布呈驼峰状，这是由近郊运输时满载与空载工况下的速度差异导致；四型客车因为营运速度的限制，在平缓路段速度分布较为集中于最大速度92 km·h-1。

(2)不同车型在相同线形路段速度分布显著不同，客车车型在平缓路段速度分布表现为分散，在连续上坡路段相对集中，货车车型速度分布在平缓路段集中，在连续上坡路段分散，变化趋势正好相反，因此，在山区高速公路采取分路段和分车型的速度管理方式是有必要的。

(3)相比平缓路段，连续上坡路段各车型的速度特征值明显下降，但相同路段上部分车型间的多个速度特征值仍较为接近；在车速离散性方面，连续上坡路段速度离散性大于平缓路段，发生追尾事故的风险水平更高，需要加强速度管理。

(4)运用k-medoids 算法对山区高速平缓路段和连续上坡路段不同车型进行聚类分析，并在此基础上根据车型的速度特征进行优化。优化后分类结果如下：平缓路段车型分为4 类，1 类为一型客车，2 类为二型～四型客车，3 类为一型货车，4 类为二型～六型货车；连续上坡路段车型分为4 类，1 类为一型～四型客车，2类为一型和三型(空载)货车，3类为二型～四型货车(三型为满载)，4类为五型和六型货车。在相应分类中给出了1～2种代表车型，该车型分类结果能够为山区高速公路速度管理和道路线形设计提供数据支持和理论依据。