面向设计重用的复杂机械三维CAD装配模型关键功能零件识别方法
2022-10-29韩周鹏周子涵田晨恺
韩周鹏,周子涵,田晨恺,刘 永,巴 黎
(西安理工大学 机械与精密仪器工程学院,西安 710048)
0 引言
随着计算机辅助设计系统在工业界的广泛应用,企业积累了大量的三维CAD装配模型,它们是企业新产品开发时,可借鉴、重用的重要知识资源。相对于零件模型,三维装配模型蕴含有丰富的设计信息,通过零件装配所体现的结构信息,不仅体现了设计者的设计意图、设计经验等知识,也能更好地与用户需求、产品功能、产品设计方案等问题对应和衔接[1]。
在借助计算机辅助设计系统进行复杂机械产品结构设计过程中,设计者通常是根据产品功能、性能、参数等需求,进行产品三维CAD模型的结构设计。产品原有设计者在产品设计过程中的设计意图、设计公理、功能、关键结构、模块结构等知识未能通过三维CAD装配模型直接体现[2],导致企业设计经验不足或缺少对原有产品知识储备的设计者较难理解、重用原有三维CAD装配模型。特别是对于企业引入的三维产品模型,模型相关信息可能存在丢失、不完整以及设计者自身设计知识与经验不足,仅仅通过三维装配模型信息较难理解三维装配模型的原有设计意图,进而制约着三维装配模型重用质量与效率。对复杂机械三维CAD装配模型的设计知识发掘,捕获三维装配模型所蕴含的功能、关键零件、关键装配结构[3]、通用设计结构[4]等知识,可以有效还原产品的设计意图,有助于其他设计者对原有设计知识的理解,启发设计者创造性思考,促进产品设计创新[5]。
对于单个复杂机械三维装配模型,零件数量繁多且装配约束关系也相对复杂,所蕴含的具有重用价值的潜在知识仅仅通过三维CAD装配模型难以显性体现。尤其是引进的外来产品三维模型,对原有设计信息进行捕获、吸收、理解,可以有效促进模型设计重用和产品设计创新。三维CAD装配模型的模块[6,7]识别弥补了产品模块设计意图缺失、不完整的缺陷。发掘三维CAD装配模型中重要的子装配体[8,9],设计者可以关注重用价值较高的重要结构信息以备设计重用。Han等人[3]考虑零件多源属性信息识别复杂三维CAD装配模型的关键装配结构,权重确定依赖于人员设定,主观性较强,所识别出的关键结构准确度不高。在此基础上,郝丽等人[10]利用粗糙集来确定零件多源属性权重,对装配体中关键零件进行识别,该过程相对复杂且侧重于零件自身属性信息,缺少对装配体拓扑结构特性分析。
为了提高复杂机械三维CAD装配模型关键功能零件识别的客观性与准确性,以促进设计者对三维装配模型隐藏知识的理解,提高三维装配模型重用质量与水平,本文提出一种复杂机械三维CAD装配模型关键功能零件识别方法。建立三维CAD装配模型的装配网络,借助复杂网络中心性指标分析三维装配模型拓扑结构特性,以此评价零件在三维装配模型拓扑空间位置的重要程度;设计一种基于AHP与TOPSIS的零件节点多属性重要度评价方法,从而识别出三维装配模型的关键功能零件。
1 三维装配模型的装配网络
1.1 三维装配模型的装配网络构建
为了便于分析机械三维装配模型中不同零件之间的重要性及零件装配约束关系,将装配模型中零件划分为两大类:紧固零件和功能零件。其中,连接件是指用于紧固连接的一类零件,主要包括螺栓、螺钉、螺母、垫片、键、销、轴承等起紧固、密封作用的零件;功能零件则指除紧固零件外的、具有一定的功能特性的零部件[3]。
三维CAD装配模型由多个零件组合而成,而且不同零件之间具有复杂的装配约束关系。若将三维装配模型中的零件看作为节点,零件属性信息作为节点属性;将装配零件之间存在的连接关系当作为节点间的边,装配连接属性作为边属性;那么三维装配模型实质可以看作为一个复杂网络模型。基于复杂网络的理论和方法,可以建立复杂机械三维CAD装配模型的装配网络,表示为:

其中,V表示三维装配模型的零件集合,V={v1,v2,v3,…vn},vi为装配模型的零件i,n为零件数量。E表示装配零件之间连接关系集合,E={e1-2,e1-3,e1-4,…eij},eij表示零件i与零件j之间存在装配连接关系。
VS表示零件节点属性信息集合,PS={ps1,ps2,ps3,…psn},n为三维装配零件数量,psi为零件i的属性信息集合。ES表示边的属性信息集合,ES={es1-2,es1-3,es1-4,…esij},ESij包括装配零件i、j的之间接触面信息、连接类型等装配连接信息。
1.2 装配拓扑结构特性分析
三维CAD装配模型依据一定的装配约束组合在一起,每个零件在装配体中具有其特定的空间位置和拓扑特性,以此来实现产品的性能与功能。复杂网络中心性指标如度数中心性、紧密度中心性介数中心性[11]和互信息中心性[12]可以有效衡量节点在复杂网络系统的重要程度。鉴于此,本文利用以上中心性指标来分析、评价三维装配模型的装配拓扑结构特性,从装配拓扑结构特性角度评价零件在三维装配模型中的重要程度。
1)零件节点的邻接矩阵A
三维装配模型中aij表示零件i和零件j之间的面接触连接关系。若零件i和零件j存在面接触,则aij=1;否则,aij=0。零件邻接矩阵ANÍN可表达为:

式(2)中N表示装配网络的零件节点总数。
2)零件节点的最短距离dsij
节点v1与vj之间的连通路径会存在多条,dsij表示节点i到节点j之间最短路径距离,三维装配模型中可反映出零件i与零件j的邻近程度。假设任意相邻节点之间的边距离为1,节点自身距离为0,零件节点之间的最短路径距离dsi采用Dijkstra计算[13]。
3)零件节点的度中心性
度中心性可以反映节点在网络中的影响力,装配模型中零件i的度中心性反映与零件i有装配连接关系的零件数量,度中心性越大,表明零件i对整个三维装配模型的影响越大。零件节点i的度中心性DC(i)可表达为:

式(3)中ki表示装配网络中与零件节点i相连接的边数。
4)零件节点的紧密中心性
零件节点的紧密中心性反映零件居于装配模型拓扑几何中心的程度。紧密中心性越大表明零件越靠近装配体拓扑空间中心位置,相应地该零件在装配模型中的空间位置越重要。零件节点紧密中心性CC(i)可表达为:

5)零件节点的介数中心性
复杂网络的节点介数用于衡量个体节点在整个复杂网络结构中的影响范围程度,节点i的介数与复杂网络中所有的最短路径经过节点i的数量有关。装配模型中零件i的介数反映出该零件在装配体中连通其他零件程度,可用来表征零件对装配体中其他零件的影响范围程度。零件节点i的介数越大,说明零件i在装配体中的影响范围越大。装配网络中零件节点介数为BC(i),则:

式(6)中σst表示零件节点s到节点t间的最短距离数量;为节点s到节点t之间最短路径中经过节点i的数量。
6)互信息中心性
互信息中心性从网络拓扑结构的特点来衡量节点重要程度,综合考虑节点的信息量来评估节点的重要性。零件节点的互信息中心性可以描述零件自身及装配信息的相对重要程度。零件节点i的互信息中心性CI(i)表示节点i与其他零件节点的互信息之和,表达为:

式(7)中deg(t)表示零件节点t的度数。
以三维装配模型的装配网络为对象,利用复杂网络中心性分析三维装配模型的拓扑空间特性,基于复杂网络中心性指标分别从装配零件空间位置、装配影响程度、装配接触面等方面定量评价三维装配模型中零件的重要程度,客观定量准确地识别出三维装配模型中重要度较高的关键功能零件,促进设计者对三维装配模型的吸收、消化与理解,在三维装配模型设计重用过程中更加重视关键零件,对关键零件的设计、制造、装配等环节提供全方位的质量与性能监测。
2 基于多属性决策的关键功能零件评价
零件节点中心性指标可以从网络拓扑结构的不同角度刻画零件在三维装配模型中的重要程度,避免了单纯地依赖一个指标来评价三维装配模型中零件的重要性具有一定的局限性,本文综合考虑以上节点中心性指标,将每个中心性指标作为一个条件属性,基于多属性决策实现对零件节点重要度的综合评价。
1)基于AHP的节点中心性指标权重确定
零件节点中心性指标权重影响着零件重要度评价结果,为了克服人为或专家打分设置权重带来的主观干扰,尽最大程度客观准确地实现三维装配模型零件重要度评价,本文利用层次分析法(AHP,Analytic hierarchy process)来确定零件节点中心性指标权重,具体过程如下:
(1)成对比较矩阵。通过标度法来对每一中心性指标进行两两比较,零件节点中心性指标重要度对比关系如表1所示。
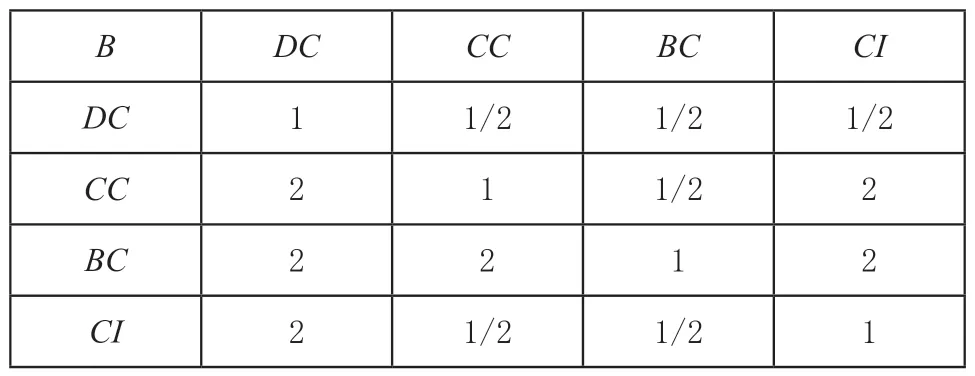
表1 节点中心性指标重要度对比值
(2)一致性检验。为了对比矩阵元素设置的更为合理,需要判断矩阵达到了规定标准,否则需要对对比矩阵进行修正,经一致性检验[14],得到各相关指标权重的值分别为wDC=0.1381,wCC=0.2761,wBC=0.3905,wCI=0.1953。
2)零件节点重要度综合评价的多属性决策模型
零件节点重要度评价实质上是将每个零件看作一个方案,零件节点中心性多个评价指标分别作为节点的属性,即各个方案的属性;那么零件节点重要度评价则可转化为一个多属性决策问题,决策准则为各个方案在装配网络的重要程度。
对于包含有N个零件节点的装配网络,对应的决策方案集合F可以表达为:
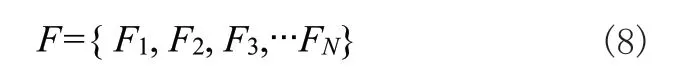
装配网络所对应的方案属性集合S可表达为:
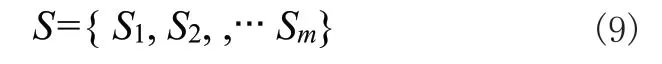
式(9)中m=4,S1-4分别代表零件节点中心性指标DC、CC、BC、CI。
决策矩阵X表达为:
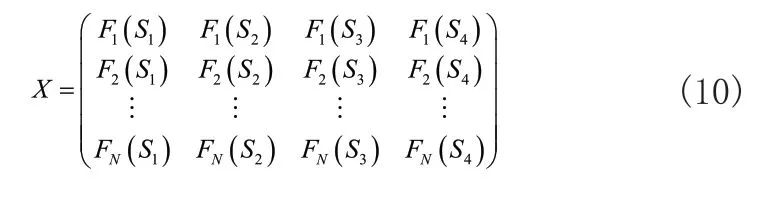
式(10)中Fi(Sj)表示零件节点i的第j个中心性指标值(i=1,2,…N;j=1,…m)。
零件节点重要度评价方案中各个指标之间存在关联性,且各指标量纲不同,为了便于计算,需要对决策矩阵X作归一化标准处理。由于本文中节点中心性度量的各个指标均为效益型,即数值越大重要度程度越高,采用如下归一化处理:

归一化处理后的规范决策矩阵表示为R=(rij)NÍm。则加权规范决策矩阵Y可表示如式(12)所示:

式(12)中权重wj的计算采用上述AHP确定,对应关系w1=wDC,w2=wCC,w3=wBC,w4=wCI。
(3)基于TOPSIS的关键功能零件评价
TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)是一种逼近理想解的排序法,作为多属性决策中有效的方法之一,其已经得到广泛应用[15]。其基本过程是构建多属性问题的正、负理想解,然后判断评价对象与正理想解、负理想解的接近度来评测方案的优劣。该方案简单易于实施,无属性数量限制,结合AHP方法能够相对客观定量地评价零件节点的重要程度。
在加权规范矩阵Y的基础上,确定正理想决策方案Y+与负理想决策方案Y-。

每个方案到正理想决策方案Y+与负理想方案Y-的距离D+、D-表达为:

方案i的贴近度Ci表达为:

基于TOPSIS的三维装配模型关键功能零件评价具体过程如下:
输入:三维装配模型的装配网络邻接矩阵A;
输出:C:零件节点的综合重要度;K:关键功能零件;
步骤1:零件节点中心性计算。根据式(3)~式(7)计算三维装配模型的复杂网络A节点度中心性DC、紧密中心性CC、介数中心性BC和互信息中心性CI。
步骤2:决策矩阵构建。根据式(8)~式(10)建立三维装配模型零件节点重要度决策矩阵X。
步骤3:规范决策矩阵R。根据式(11)、将决策矩阵X归一化、标准化处理。
步骤4:建立加权规范矩阵Y。节点中心性指标的权重利用AHP计算确定,利用式(12)建立加权规范矩阵Y。
步骤5:根据式(13)、式(14)确定正、负理想决策方案Y+和Y-。
步骤6:根据式(15)、式(16)计算每个方案Yi到正负理想决策方案Y+和Y-的距离D+、D-。
步骤7:根据式(17)计算每个方案Yi到理想决策方案的贴近度Ci。
步骤8:根据每个方案的贴近度C(即零件的重要度),进行方案排序择优确定关键功能零件。
步骤9:输出三维装配模型的零件重要度和关键功能零件。
3 实例验证
以某蜗轮蜗杆减速器三维CAD装配模型为例,提取该三维CAD装配模型的装配关系信息,构建对应的装配网络模型,利用本文所提方法对蜗轮蜗杆减速器三维CAD装配模型关键功能零件进行识别。图1为某蜗轮蜗杆减速器的三维CAD装配模型示意图,表2为该三维装配模型的零件信息。
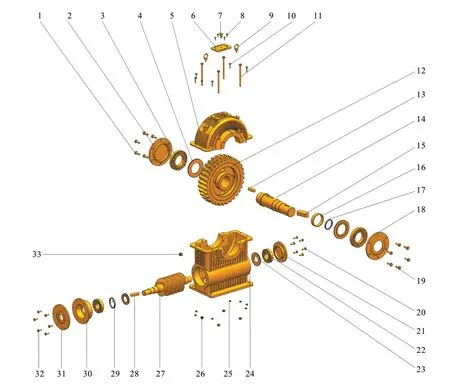
图1 蜗轮蜗杆减速器三维装配模型示意图

表2 蜗轮蜗杆减速器零件信息
通过提取蜗轮蜗杆减速器三维CAD装配模型的装配约束、零件属性信息,可获取零件之间的接触关系、零件名称等属性信息。以此可构建该装配模型所对应的复装配网络邻接矩阵A如图2所示。其中,功能零件节点集合为{v2,v5,v6,v12,v14,v16,v18,v21,v24,v27,v30,,v31},连接件节点集合为{v1,v3,v4,v7,v8,v9,v10,v11,v13,v15,v17,v19,v20,v22,v23,v25,v26,v28,v29,v32,v33}。

图2 蜗轮蜗杆减速器的装配网络邻接矩阵A
1)零件节点中心性指标计算
由于在三维装配模型装配关系提取过程中,已识别出了功能零件与紧固件,为了提高计算效率,本文方法只对已筛选出的功能零件进行重要评价。利用式(2)~式(7)计算蜗轮蜗杆减速器三维装配模型的装配结构拓扑特性,零件节点中心性指标计算结果如表3所示。
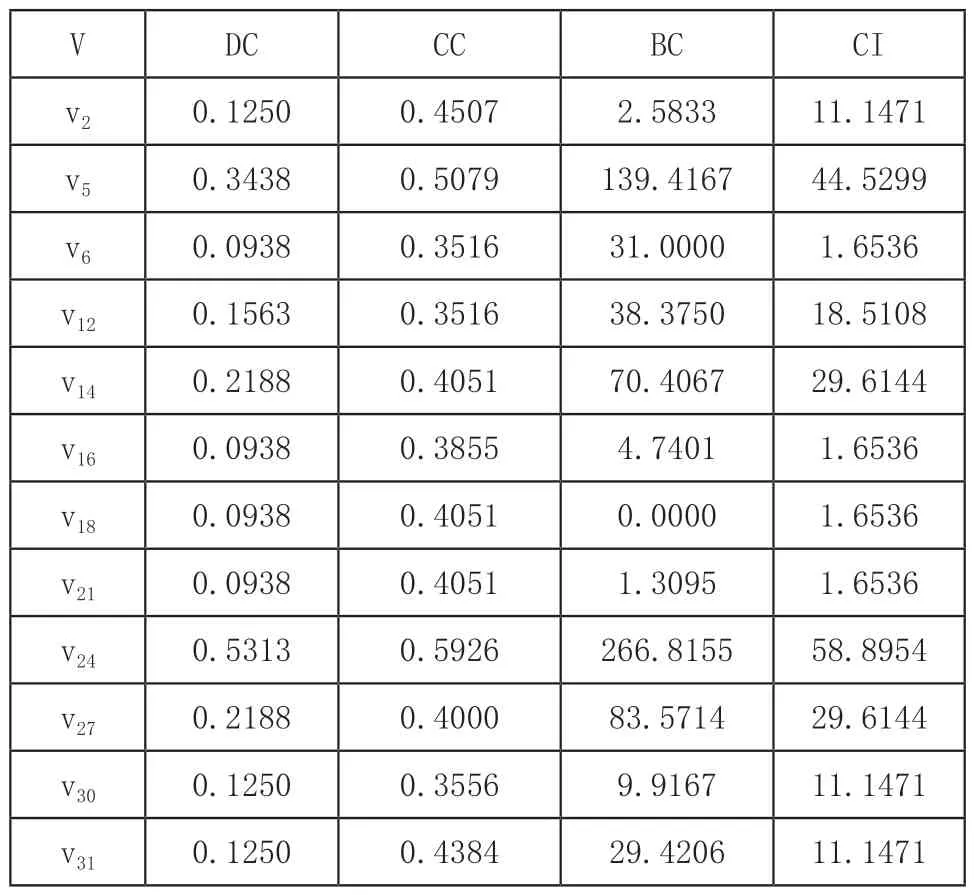
表3 零件节点中心性指标结果
2)决策矩阵构建及规范化
根据式(8)~式(10)可以建立蜗轮蜗杆减速器三维装配模型的初始决策矩阵X,如表4所示。
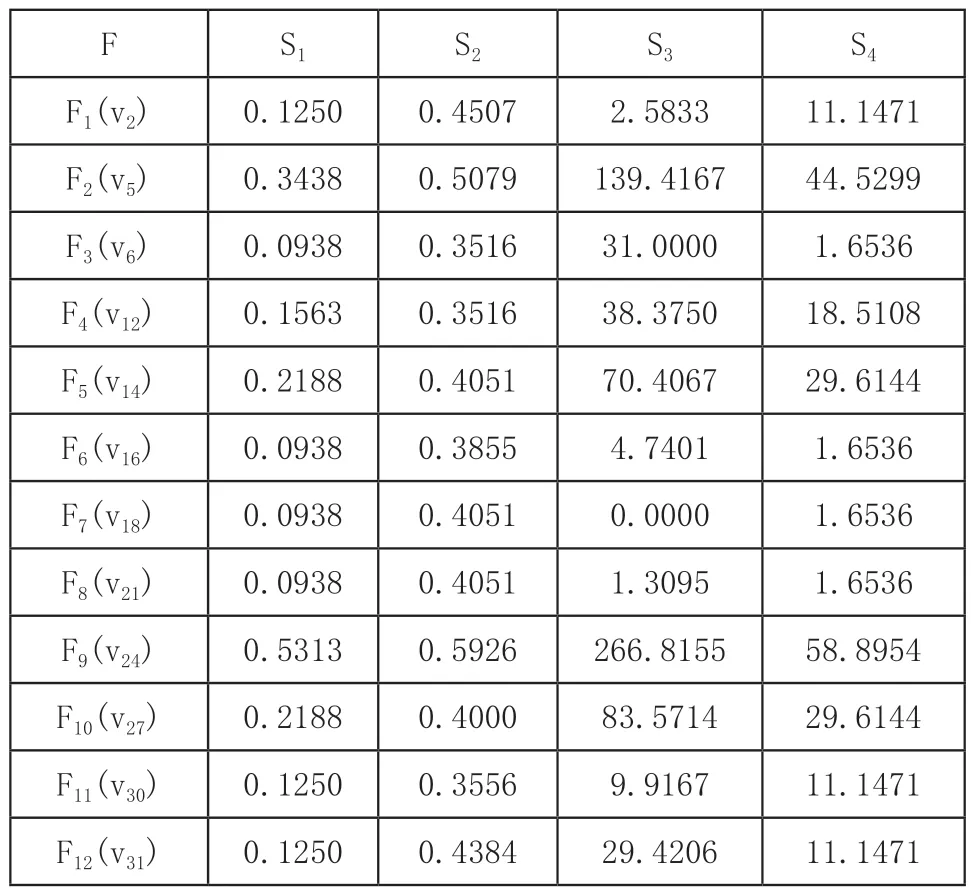
表4 初始决策矩阵X
利用式(11)对决策矩阵方案指标数值归一化处理,并基于AHP确定属性S1-S4各自的权重值,由上文可知w1=0.1381,w2=0.2761,w3=0.3905,w4=0.1953。根据式(12)可得到加权规范决策矩阵Y,如表5所示。

表5 规范决策矩阵Y
4)基于TOPSIS的关键功能零件评价
利用式(13)~式(17)计算每一种方案与理想方案的贴近度即得到零件的重要度,如表6所示。

表6 三维装配模型零件节点贴近度及排序
由于贴近度表示方案重要程度,由表6可知零件重要度排序前3的方案为F9(v24)、F2(v5)和F10(v27),分别代表着蜗轮蜗杆减速器的箱座、箱盖与蜗轮轴。因此,箱座、箱盖与蜗轮轴被当作蜗轮蜗杆减速器三维CAD装配模型的关键功能零件,其在设计、制造、装配过程中比较重要,在三维装配模型重用时需要重点关注以上关键功能零件。同时,本文方法与文献[10]方法进行了对比,这两种方法识别的关键功能零件基本一致,但该文献考虑了零件多源属性信息,采用粗糙集理论进行评价,增加了重要度评价的主观性与复杂性,本文采用AHP计算装配拓扑特性中心性指标权重更加客观,减少了人为主观干扰。
4 结语
通过本文方法可以提前识别三维CAD装配模型的关键功能零件,为设计人员在三维模型设计重用时提供参考、加深对重用模型的理解与吸收,让设计者关注关键功能零件的设计、加工与装配等环节。该方法基于复杂网络的拓扑特性指标分析三维装配模型中零件重要性,利用AHP与TOPSIS对三维装配模型零件重要度评价,相对客观准确地识别出三维装配模型所蕴含的关键功能零件。该方法减少了人为主观因素的干扰且具有较高的柔性,能够适应各类复杂机械三维CAD装配模型关键功能零件的识别,算法过程简便易于实施。
