基于蒙特卡罗抽样的简化核电站SBO事故的风险指引安全裕度分析
2022-10-29李朝君
李朝君,张 盼,韩 治,郑 洁,陈 妍,李 春,依 岩
(生态环境部 核与辐射安全中心,北京 102400)
从2008年起,美国核电站开始申请延寿至60年,一些核电站计划申请延寿至80年。美国早期核电站设计寿期一般是40年,寿期延长至设计寿期两倍的做法对美国核电运行和监管带来挑战。为应对挑战,美国爱达荷国家实验室(INL)发布了轻水堆可持续发展项目的综合计划[1],包括4个研发方向:核材料老化和退化、先进轻水反应堆燃料开发、先进仪控技术以及风险指引的安全裕度特性分析(RISMC)技术。目前,美国已基本搭建了RISMC的计算平台,并开展试点案例的分析计算[2]。法国电力研究所[3]、韩国原子能研究所等机构也陆续开展了有关RISMC的研究,近几年我国在RISMC方法等方面也开展了一些研究[4-6]。本文重点阐述风险指引安全裕度(SM)与核电传统安全裕度的区别,在风险指引的安全裕度的计算框架下对核电站全厂断电(SBO)事故进行研究,重点研究蒙特卡罗抽样方法下的SBO事故下的风险指引的安全裕度定量化技术,开展蒙特卡罗抽样下的简化核电站SBO事故的实例计算及分析。
1 风险指引的安全裕度
安全裕度是核电站早期设计中的重要理念之一。2016版的HAF 102《核动力厂设计安全规定》[7]关于安全裕度的规定“设计必须提供适当的裕度,以考虑有关老化、中子辐照脆化和磨损机理,以及与服役年限有关的性能劣化的可能性,从而保证安全重要物项在其整个设计寿期内执行所必需的安全功能的能力”。这里裕度的定义为安全变量的能力(Capacity,C)与负载(Load,L)的比值,也可定义为安全变量的能力与负载的差值,通常是确定性的安全裕度。在目前的核电站针对设计基准事故的设计和许可中,特定安全变量(如燃料包壳温度等)的安全裕度通常是安全变量的安全限值与负载的差值,其中安全限值通常被保守的设置在低于能力分布下限值的某个特定值,负载则通常是系统程序(如Relap、Melcor等)的计算值[8]。
核电站安全变量的能力分布不是一成不变的,随着核电站在运时间的不断增加,可能会随着老化等因素向承载能力变小的方向移动,而负载分布也可能随着高燃耗、功率提升等因素向负载变大的方向变化。这时传统的安全裕度评价方法计算的安全裕度可能过小,这将在制定核电站延寿、长期运行以及扩展功率等管理决策时造成重大影响。为了更客观现实的评价核电站在整个寿期内的安全裕度,保障核电站安全性的同时兼顾经济性,美国在RISMC方法中提出风险指引的安全裕度的概念,其可定义为:在模拟的大量事故情景下,核电站安全变量(如燃料包壳温度、燃料包壳应力、燃料包壳氧化物厚度等)的负载超过能力的概率,数学上表达为P(L>C)[9]。此裕度不再是能力与负载的比值或差值的确定性计算裕度方法,而是概率性的计算裕度方法,也称概率安全裕度,如图1绿色面积部分所示。

图1 风险指引的安全裕度示意图Fig.1 Scheme of risk-informed safety margin
2 风险指引的安全裕度的计算
2.1 风险指引的安全裕度的计算方法框架
美国INL在实施RISMC时,首先开展风险模拟和物理模拟产生各种情景以及相应的情景参数,然后将各情景参数传递给系统程序(如物理、热工等程序),系统程序计算的过程物理参数也动态反馈给情景,最后计算出各种情景下安全变量特性及情景概率,用统计分析方法计算安全变量的安全裕度及其不确定度,最终支持管理决策的制定,具体计算框架如图2所示。实现过程中,RISMC方法需要通过搭建计算平台,计算机编程自动产生各种情景参数,计算每个情景的发生概率,采用系统程序计算每个情景下的重要物理/热工参数,并判断这些参数在每个情景下是否失效,最后计算风险指引的安全裕度。

图2 风险指引的安全裕度的计算框架Fig.2 Framework of risk-informed safety margin calculation
在情景产生中,常用的方法有蒙特卡罗抽样方法、离散动态事件树方法和自适应算法等。本文重点研究基于蒙特卡罗抽样产生情景下风险指引的安全裕度方法在核电厂SBO事故分析中的应用,并以燃料包壳温度作为安全变量。
2.2 基于蒙特卡罗抽样的风险指引的安全裕度计算
在蒙特卡罗抽样方法下,将n个情景参数分别传递给系统程序进行模拟计算,比较模拟计算的燃料包壳温度与从能力分布随机产生的燃料包壳失效温度,统计所有情景模拟计算的负载大于随机能力的个数[8,10],则概率安全裕度定义为:
(1)
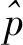
(2)

3 基于简化核电站的SBO事故风险指引的安全裕度计算
3.1 简化核电站SBO事故模型
为研究蒙特卡罗方法下RISMC中概率安全裕度的不确定性分析方法以及蒙特卡罗抽样次数的估算方法,探究RISMC方法应用到核电站事故分析中需要关注的关键因素,本文参考INL在RISMC研究中关于简化压水堆模型SBO事故分析的参数[12],建立了简化核电站的热工水力模型节点图,如图3所示。此简化核电站热工水力模型模化了反应堆压力容器模型的下降通道、下封头、堆芯和上腔室,堆芯部分的3个平行的燃料通道和1个旁通通道,两个主环路(每一个环路由热管段、1个热交换器及其二次侧管段、冷管段和1个主泵组成)以及稳压器。

图3 简化核电站的节点示意图Fig.3 Node diagram of simplified nuclear power plant
本文在进行简化核电站模型SBO事故计算时,假设如下:200 s瞬态开始SBO事故,201 s时厂外电丧失,电厂立即停堆,随后主泵惰转,应急柴油机失效,造成冷却系统不可用,丧失热阱。
3.2 计算流程
RISMC中考虑应急柴油机在不同恢复时间的需求失效,因此应急柴油机的恢复时间t是关键参数,并用恢复时间生成不同事故情景;同时要考虑燃料包壳失效温度分布,因此燃料包壳失效温度PCTfail也是关键参数。关于应急柴油机的恢复时间的分布,本文参考相关文献[8],假设应急柴油机的恢复时间(单位为s)服从正态分布,正态分布为Normal(2 900,200,50)。本文假设燃料包壳失效温度分布与参考文献一致,服从Triangular(1 255.37,1 477.59,1 699.82)的三角分布,可以看到三角分布的众数1 477.59 K对应确定论中燃料包壳损坏温度1 204 ℃。
基于蒙特卡罗抽样方法的SBO事故分析计算流程如图4所示,关键步骤如下:1) 基于上述对应急柴油机的恢复时间和燃料包壳失效温度分布的假设,采用蒙特卡罗抽样方法对两个参数随机抽取一定量数据,并组成相应个数情景;2) 将抽样参数传输给热工水力程序的SBO输入卡,生成对应个数的输入卡,进行并行计算;3) 计算任务时间内,计算每个情景下的燃料包壳的温度,并与相应情景下的燃料包壳失效温度比较,判断最大燃料包壳温度是否大于燃料包壳失效温度;4) 计算概率安全裕度以及不确定性。

图4 基于蒙特卡罗抽样方法的风险指引的概率安全裕度计算流程Fig.4 Calculation flow of risk-informed probabilistic safety margin based on Monte Carlo sampling
3.3 计算结果分析
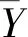
(3)
蒙特卡罗抽样次数估算为:
(4)
(5)
(6)
其中:zα/2为标准正态分布右尾面积是α/2时对应的横坐标,zα/2=1.96;ε为相对误差;s为样本标准差;Δ为绝对误差,本文给定Δ=0.01;n绝对误差估计为绝对误差方法下的抽样次数;n相对误差估计为相对误差方法下的抽样次数。
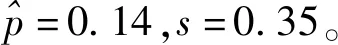
(7)

选择相对误差方法计算抽样次数。由式(6)计算得出,相对误差为5%时,抽样次数为9 604次。9 604次拉丁超立方蒙特卡罗抽样下,燃料包壳失效概率均值为0.125,样本标准差为0.33,在95%置信度下,均值的绝对误差为0.006 6。图6示出9 604组风险情景下风险指引的安全裕度负载和能力直方图。
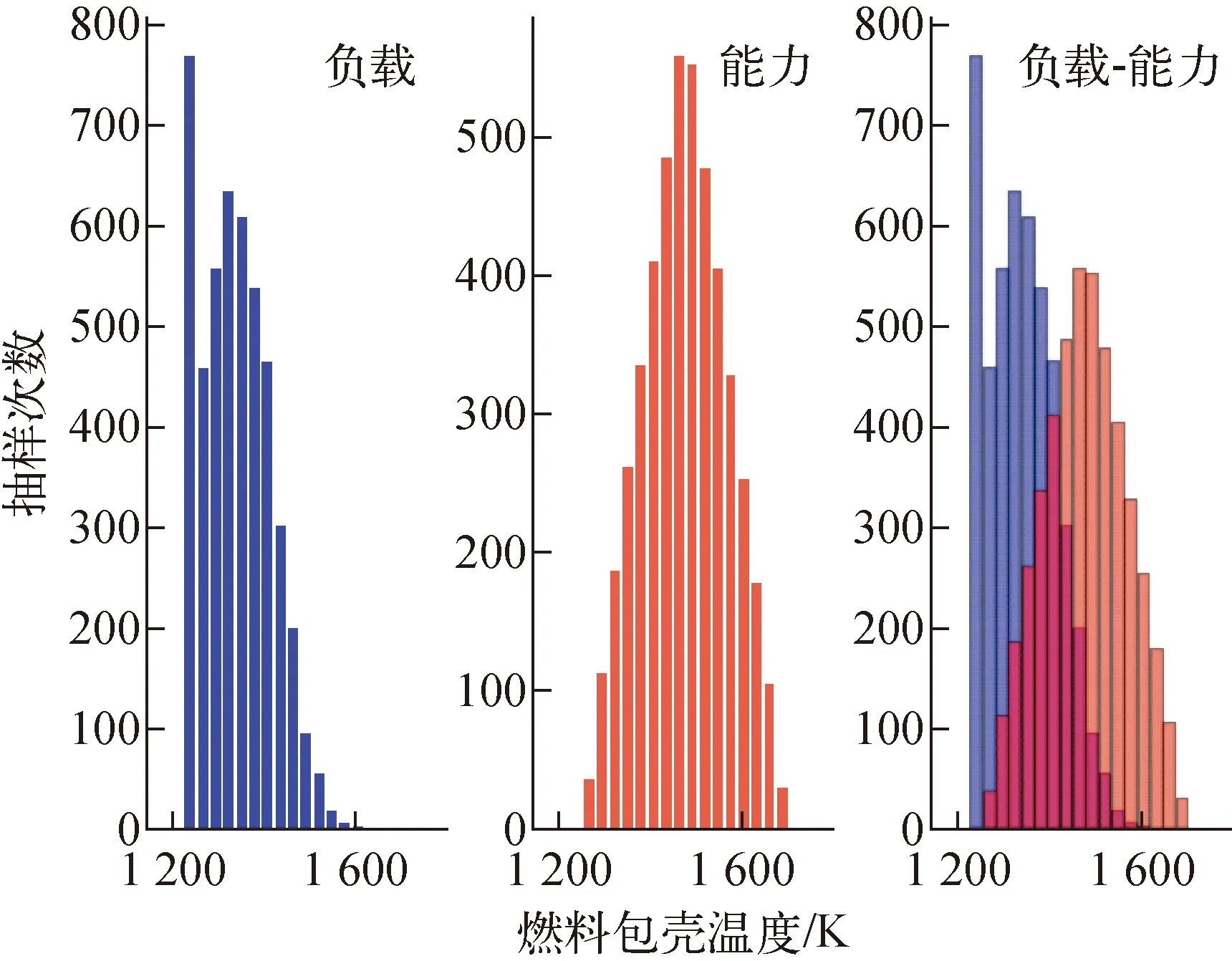
图5 4 706组风险情景下的风险指引的安全裕度负载和能力直方图Fig.5 Risk-informed safety margin load and capability histograms under 4 706 risk scenarios
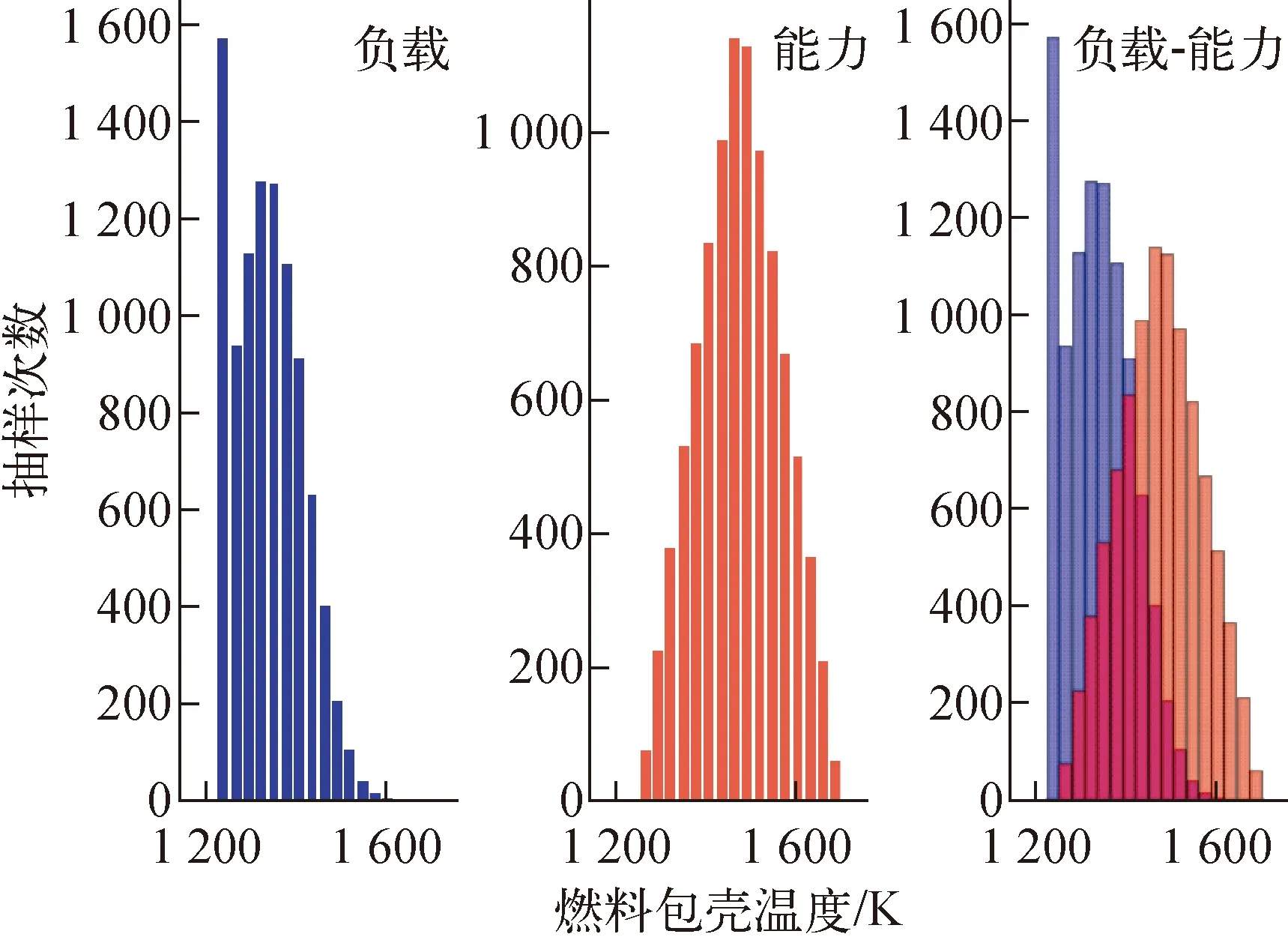
图6 9 604组风险情景下的风险指引的安全裕度负载和能力直方图Fig.6 Risk-informed safety margin load and capability histograms under 9 604 risk scenarios
可以看到,通过绝对误差和相对误差两种方法都可计算得出相应的抽样次数。绝对误差0.01下应抽样4 706次,燃料包壳失效概率均值为0.12,运行时间和存储需求为1 901 min和419 GB;相对误差5%下应抽样9 604次,燃料包壳失效概率均值为0.125,运行时间和存储需求为3 878 min和885.1 GB,燃料包壳失效概率均值存在约4.2%的差异。在实际工程中,可根据特定问题选择绝对误差或相对误差两种方法计算抽样次数。相对误差和绝对误差可相互转换,若采用相对误差计算抽样次数,由式(6)可看出相对误差要求越小、失效概率均值越小所需的抽样次数越多,计算所需的运行时间和存储需求也越多。5%相对误差要求下,由式(6)可估算得出失效概率均值大于0.1时,抽样次数在万次以下,失效概率均值小于0.1时,抽样次数可达数10万次。在现阶段通常计算资源配置下,建议失效概率均值大于0.1时,选择5%相对误差计算抽样次数;失效概率均值小于等于0.1时,选择10%相对误差计算抽样次数。
4 影响因素分析
4.1 抽样方法的影响
为研究抽样方法不同对计算结果的影响,完成随机抽样方法的50次和4 706次的抽样计算,并与拉丁超立方抽样方法得出的50次和4 706次的抽样计算结果进行比较,计算结果列于表1。计算过程中,应急柴油机的恢复时间t(单位为s)服从正态分布Normal(2 900,200)。
由表1可看出,抽样次数少时,随机抽样和拉丁超立方抽样两种不同抽样方法对燃料包壳失效概率均值有显著影响。抽样次数增大到一定数量后,两种不同抽样方法得到的燃料包壳失效概率均值相差不大。拉丁超立方抽样是一种分层抽样方法,相比于随机抽样具有更高的抽样精度。另外,拉丁超立方抽样相比于随机抽样给出的样本标准差更小,可有效减少抽样次数提高计算效率。在工程实践中,建议采用拉丁超立方抽样方法或其他更高效的抽样方法。
4.2 正态分布的影响
4.1节计算中假设应急柴油机的恢复时间服从正态分布,正态分布为Normal(2 900,200),为研究恢复时间的不同分布对计算结果的影响,选择应急柴油机恢复时间均值±5%来进行计算。分别对Normal(2 755,200)、Normal(3 045,200)两种分布进行计算,抽样方法采用拉丁超立方抽样,计算结果列于表2。

表1 不同抽样方法下核燃料包壳失效概率均值Table 1 Mean value of failure probability of nuclear fuel cladding under different sampling methods
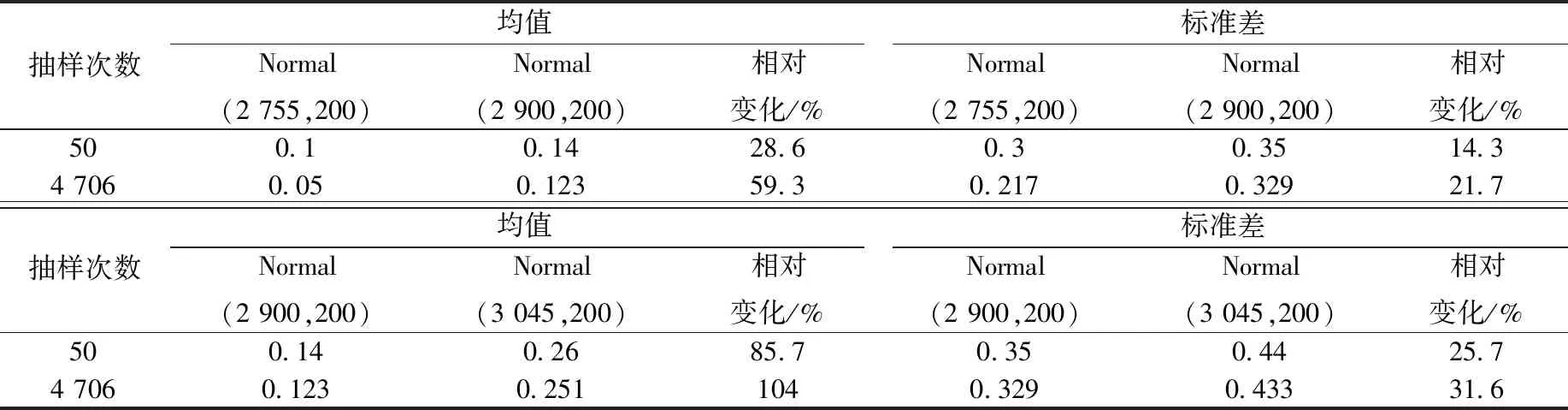
表2 不同均值分布下核燃料包壳失效概率均值Table 2 Mean value of failure probability of nuclear fuel cladding under different distributions
表2结果表明,应急柴油机恢复时间均值2 755 s时的核燃料包壳失效概率均值相比均值2 900 s时变小,均值3 045 s时的核燃料包壳失效概率均值相比均值2 900 s时变大,分布均值选择越大,平均燃料包壳失效概率越大。相比50次抽样,4 706次抽样下不同均值分布对平均燃料包壳失效概率的影响更显著。因此,在核电站风险指引安全裕度计算中,需根据试验、同类电厂数据以及工程判断等方法确定合理的关键参数分布。
5 总结
本文基于蒙特卡罗抽样产生情景的RISMC计算方法,提出了蒙特卡罗抽样方法下风险指引的安全裕度的不确定度计算方法,给出了风险指引安全裕度计算中蒙特卡罗抽样次数的估算方法。对于基于蒙特卡罗抽样的情景产生个数,本质上是需要保证计算结果准确度的可接受性,情景个数越多,概率安全裕度估计值的精度越高。具体计算情景个数时,首先可以选择绝对误差方法或相对误差方法,或将绝对误差方法和相对误差方法结合起来的方法,来确定概率安全裕度均值的精度,然后在给定绝对误差或相对误差后,可以估算模拟次数,并开展计算,最后通过终止条件等验证模拟次数的合理性。本文还对不同抽样方法、不同正态分布对核燃料包壳失效概率均值和标准差的影响进行了分析,计算结果显示这些因素对失效概率均值和标准差有显著影响。在工程实践中,建议采用拉丁超立方抽样方法或其他更高效的抽样方法以提高计算效率;同时建议失效概率均值大于0.1时,选择5%相对误差计算抽样次数,失效概率均值小于等于0.1时,选择10%相对误差计算抽样次数。