径向分层碎片床内流动特性研究

张拯政，李良星,*，马卫民，元一单，杨小明，马如冰

(1.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049；2.瑞典皇家工学院 核动力安全研究室，瑞典 斯德哥尔摩 10693；3.中国核电工程有限公司，北京 100840)

颗粒堆积多孔介质内的单相/两相流动在许多工程领域都有广泛的研究和应用，包括化学催化、农业、石油工程以及陶瓷材料等多个工程领域[1-4]。特别是在核反应堆堆芯熔融严重事故进程中，熔融堆芯材料与冷却剂相互作用后可能形成具有多孔介质结构的颗粒堆积碎片床。冷却水在碎片床内的流动阻力特性对碎片床冷却性课题研究至关重要，许多学者已针对碎片床内的单相/两相流动特性开展了相关实验和理论研究，其主要目的是研究流体在颗粒堆积床内的流动阻力特性及其控制机理[5-13]，进而开发流动阻力模型[14-18]。但已有的研究大多是基于均质颗粒堆积床进行的[19-20]，流体在颗粒堆积床内总体上沿一个方向流动，呈现一维流动特性。其中Ergun方程是目前应用最广泛的预测均质颗粒堆积床内单相流动阻力的公式，其基本形式如下：

(1)

式中：Δp/L为单位长度的阻力压降，Pa/m；μ为流体动力黏度，Pa·s；kp为渗透率，m2；ρl为流体密度，kg/m3；η为穿透率，m；J为流体表观流速，m/s；Dp为颗粒直径，m；θ为孔隙率。

(2)

(3)

然而在反应堆严重事故进程中形成的碎片床具有随机性，可能具有分层结构特征[21-22]，呈现多维流动换热特性。近期的研究[8]表明，存在多维流动换热现象的非均质结构颗粒堆积床内干涸热流密度可能远高于一维的情况，因此研究非均质的颗粒堆积床内的流动阻力特性对延缓和抑制反应堆严重事故具有科学意义以及工程价值[21,23]。

为研究非均质结构颗粒堆积床内的流动特性，本文使用两种不同尺寸的球形颗粒构建具有径向分层结构的颗粒堆积床。为对比分析，采用上述颗粒构建3个均质结构颗粒堆积床(包含2个单一尺寸颗粒堆积床、1个两种尺寸颗粒均匀混合堆积床)。首先实验研究4组床内的流动压降特性，分析其变化规律。随后开展针对性的数值模拟研究，进一步分析分层床内的流场分布，重点研究流体在分层界面处的流场，探讨其影响因素及控制机理。

1 实验研究

1.1 实验系统

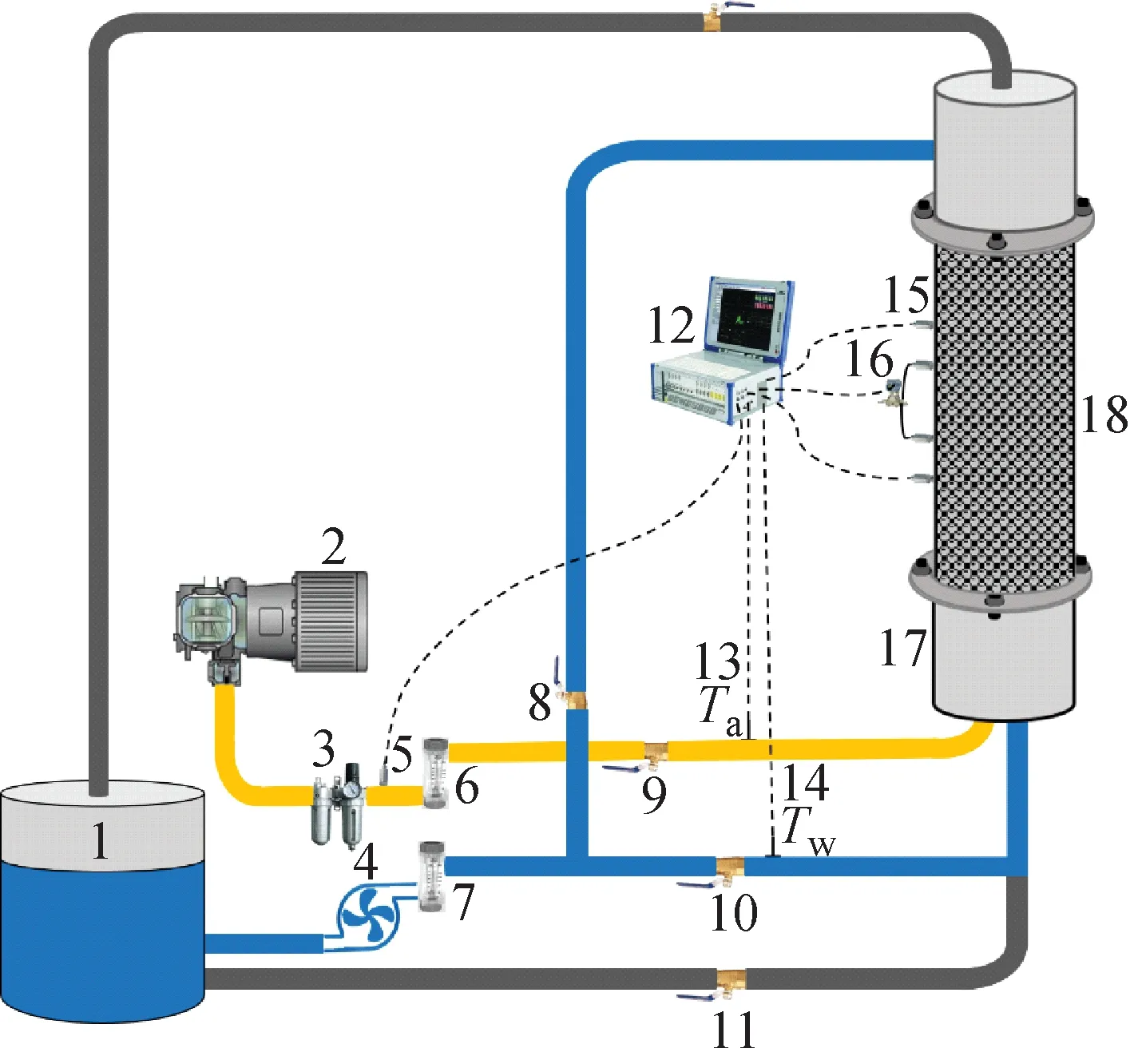
1——水箱；2——空气压缩机；3——油气分离器；4——水泵；5——压缩机出口压力传感器；6——气体流量计；7——液体流量计；8——顶部注水阀；9——气路截水阀；10——底部注水阀；11——水路旁通阀；12——数据采集系统；13——气路热电偶；14——水路热电偶；15——实验段压力传感器；16——差压变送器；17——气水混合段；18——实验段图1 DEBECO实验系统示意图Fig.1 Schematic diagram of DEBECO experimental system

为研究颗粒堆积床内的流动特性，设计并搭建了DEBECO实验系统，如图1所示。实验系统主要包括供水系统、注气系统、实验段以及数据采集系统。实验段由内径为120 mm、高度为600 mm的圆柱形有机玻璃管制成。实验段内不同测点位置的压力以及不同高度下的流动压差动态信号分别采用Omega高精度压力传感器和Rosemount3051压差变送器测量，并使用NI数据采集系统采集压力等信号，压力传感器和差压变送器的精度分别为0.25%和0.04%。为避免进出口效应影响，将取压点设计在距离实验段进出口两端一段距离处，确保压力测点落在流体的充分发展段。流体的流量由多个不同量程的Omega流量计(FL-2000)系列测控，测量精度为2%。实验过程中，去离子水在水泵的作用下自下而上流过实验段后回到水箱，实验均在大气压(约0.1 MPa)和室温条件下运行。

1.2 实验颗粒床

实验采用直径为2 mm和8 mm的玻璃圆球分别构建均质结构颗粒堆积床(Bed-1～Bed-3)和非均质结构颗粒堆积床(Bed-4)。其中Bed-1和Bed-2分别由2 mm和8 mm单一直径玻璃圆球堆积形成，Bed-3由两种颗粒按质量比为1∶1均匀混合后自由堆积形成。Bed-4由两种尺寸的颗粒分别沿实验段左右两侧自由堆积形成，两种颗粒层分别占实验段左右一半空间，因此Bed-4是具有竖直分层结构的分层颗粒堆积床。图2为4组颗粒堆积床的结构示意图。

孔隙率是颗粒堆积床流动阻力特性研究的重要参数之一，实验通过称重装填颗粒重量的方法计算颗粒堆积床的孔隙率θ，其计算公式如下：

(4)

式中：V0为实验段总体积，m3；mp为测试段内填充颗粒的质量，kg；ρp为填充颗粒的密度，kg/m3。

Bed-1～Bed-4中颗粒直径Dp、孔隙率θ、渗透率kp和穿透率η等信息列于表1。分层床Bed-4内左右两侧的颗粒各占实验段体积的1/2，实验过程中，两层中间无挡板。总体上，小颗粒堆积层的孔隙率和渗透率等均小于大颗粒堆积层。

表1 不同尺寸颗粒堆积层信息Table 1 Information of different particles layer

1.3 不同堆积结构颗粒床内单相流动实验

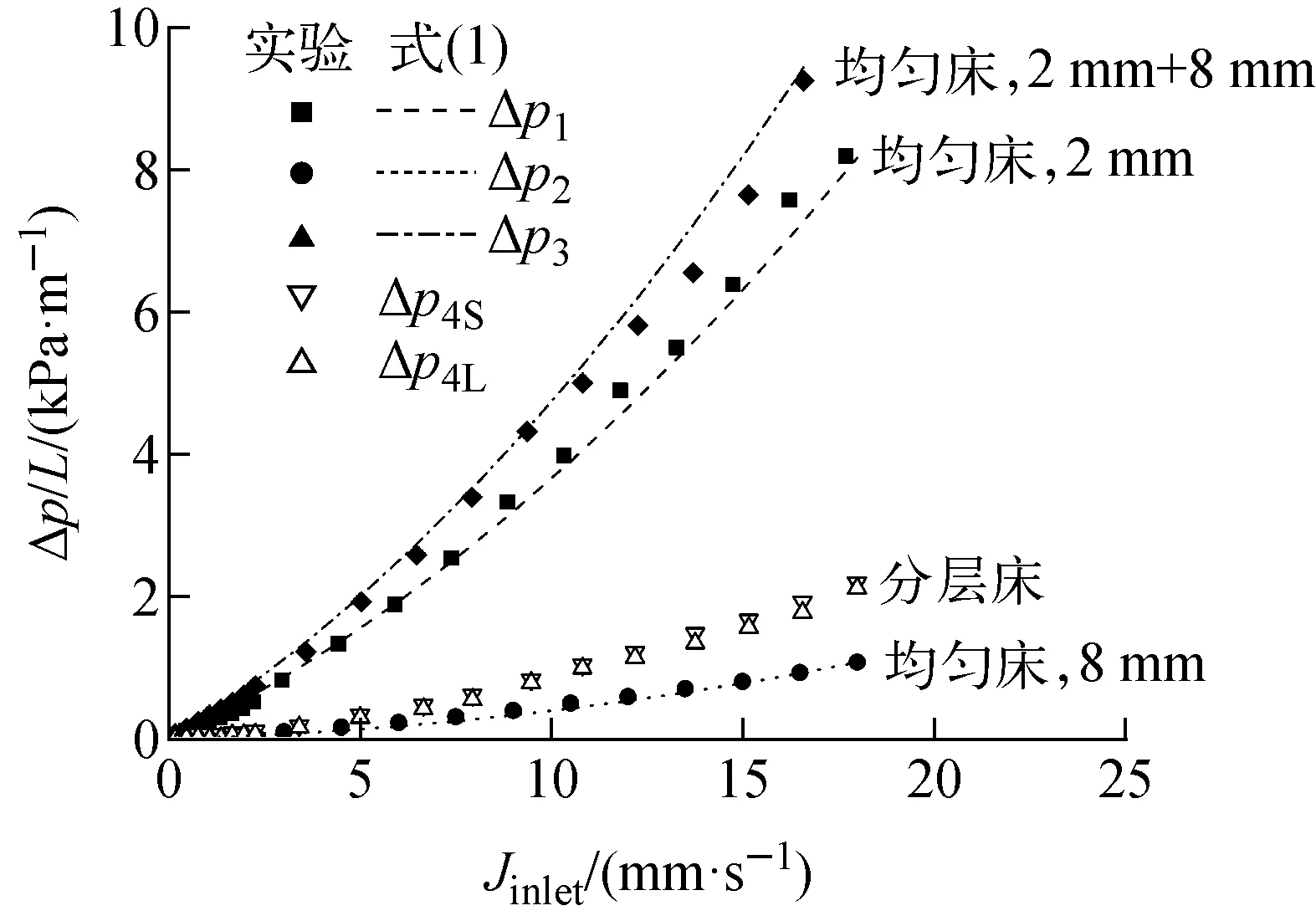
图3 Bed-1～Bed-4流动压降随流体表观流速的变化Fig.3 Variation of pressure drop with superficial flowrate of Bed-1-Bed-4

为研究不同堆积结构颗粒床内的流动阻力特性，尤其是径向分层颗粒堆积床内流动阻力特性，首先基于Bed-1～Bed-4开展了单相流动实验，去离子水自下而上通过颗粒堆积床，实验过程中利用NI数据采集系统实时监测和记录不同流速下颗粒堆积床内的流动阻力压降。不同流体流量下各堆积床内的流动压降及其变化趋势示于图3，流速对应的雷诺数Re为0～23.20，其中Re=ρlJDp/(1-θ)。图3中，Jinlet为流体表观流速；Δp1、Δp2和Δp3分别为Bed-1～Bed-3内的压降；Δp4S和Δp4L分别为组成分层床中的小颗粒和大颗粒组成的均质床中的压降；曲线分别代表采用Ergun方程(式(1))计算得到的相应均质床内的流动压降，对于均匀混合床(Bed-3)，基于文献[19]给出的中值直径计算Bed-3内的流动压降。

从图3可看到，Bed-1～Bed-4内的流动压降均随流体流量的增加而增大，Ergun方程计算值与实验测量值吻合较好，最大相对误差为10.85%。对于单一尺寸颗粒形成的堆积床(Bed-1和Bed-2)，同一流体流量下，2 mm颗粒堆积床内的流动压降显著高于8 mm颗粒堆积床内的流动压降。这主要是因为小颗粒堆积床的渗透率和穿透率较小，流动阻力较大。而同一流体流量下两种尺寸颗粒均匀混合堆积床(Bed-3)内的流动压降则大于单一尺寸颗粒形成的堆积床。分析认为，Bed-3由两种颗粒均匀混合后堆积形成，Bed-3中大颗粒形成的空隙被小颗粒进一步填充，因此Bed-3的孔隙率、渗透率和穿透率进一步降低，从而导致Bed-3内的流动压降大于Bed-1和Bed-2。

对于径向分层堆积床(Bed-4)，相同流体流量下，径向分层堆积床内小颗粒层流动压降与大颗粒层几乎相等，但远小于单一尺寸小颗粒堆积床(Bed-1)内的流动压降，略大于单一尺寸大颗粒堆积床(Bed-2)内的流动压降。根据图3中Ergun方程的计算结果，对于单一尺寸颗粒以及两种尺寸颗粒均匀混合后形成的均质堆积床，一维阻力预测模型能较好地预测其中的流动压降，这说明均质床中流体呈现一维流动特性。

对于分层床，左侧由小颗粒自由堆积形成，右侧由大颗粒自由堆积形成，每一层均可认为是单一颗粒堆积床。当流体进入分层床后，如果流体在分层床内均匀分布(类似于在均质颗粒床内的流动特性)，则由图3单一尺寸颗粒形成的堆积床结果分析可推测，分层床内小颗粒层的流动压降(Δp4S)将远大于大颗粒层内的流动压降(Δp4L)。然而实验测量得到两分层床内的流动压降基本相等。由表1可看出，小颗粒层的渗透率和穿透率均小于大颗粒层，在分层床的两颗粒层内压降相等的情况下，基于Ergun方程可得出小颗粒层的流体流量小于大颗粒层内的流体流量。换言之，流体在分层床内的流动特性与均质颗粒床内的不同，流体在分层床内可能因为渗透率不同而引起流体流量的重新分配。由于实验研究的局限性，无法获得分层床内的流场分布，为揭示分层床内的流量再分配特性，本文通过数值模拟研究，重点揭示分层堆积结构颗粒床内的流动特性，尤其是分层界面处的流场分布。

2 数值模拟研究

为进一步研究流体在分层床内的流场信息，揭示流体颗粒堆积结构变化时的流动特性，本文基于Bed-4开展径向分层床内单相流动数值模拟研究。

2.1 湍流模型

在目前的研究中，采用标准k-ε模型模拟多孔介质内的流场。

连续性方程为：

(5)

动量方程为：

(6)

其中：τij为表面张力；Fi为动量源项。

湍动能和湍动耗散率方程分别如下：

Gk+Gb-ρε-YM

(7)

(8)

(9)

其中：k为湍动能；σk为动量扩散率与湍流动能扩散率之比；Gk和Gb分别为由平均速度梯度和浮力产生的湍流动能；ε为湍动耗散率；YM为脉动膨胀对可压缩湍流的贡献；σε为动量扩散率与湍流耗散扩散率之比；C1ε、C2ε、C3ε和Cμ为经验常数；μT为湍流黏性系数。

2.2 多孔介质数学模型

在多孔介质中，流固相互作用较强，通过增加动量源项对多孔介质进行建模。在Fluent中，力的源项表示为：

(10)

其中，C2为惯性项系数。式(10)右边第1项为黏性损失项，第2项为惯性损失项，如果流体流动缓慢，第2项可忽略。文献中已有大量的实验来确定不同类型多孔介质的压降和速度之间的关系，Ergun方程是多孔介质填充床中最广泛采用的经验方程，通过对比式(1)、(10)可得到：

(11)

需要说明的是，已有的针对流体在非均质多孔介质结构内的流动现象，多采用在Darcy-Forchheimer模型(Ergun方程属于Darcy-Forchheimer模型)基础上添加Brinkman项进行计算，但同时有研究指出，只有当多孔介质空隙率大于0.6时Brinkman项才能使用[24]。由表1可看出，本研究中所有颗粒床的孔隙率均在0.38以下，因此数值模拟过程没有考虑Brinkman项。

2.3 数值模拟方法验证

根据已知参数对实验段进行几何建模，将实验段简化为一内径120 mm、高度600 mm的圆柱形管道，然后对几何模型进行网格划分。为保证网格质量，采用结构化网格，图4为实验段网格示意图，其中管道入口边界条件设置为速度入口，出口边界条件设置为压力出口。其中流体入口表观流速模拟范围为0.1～18 mm/s。

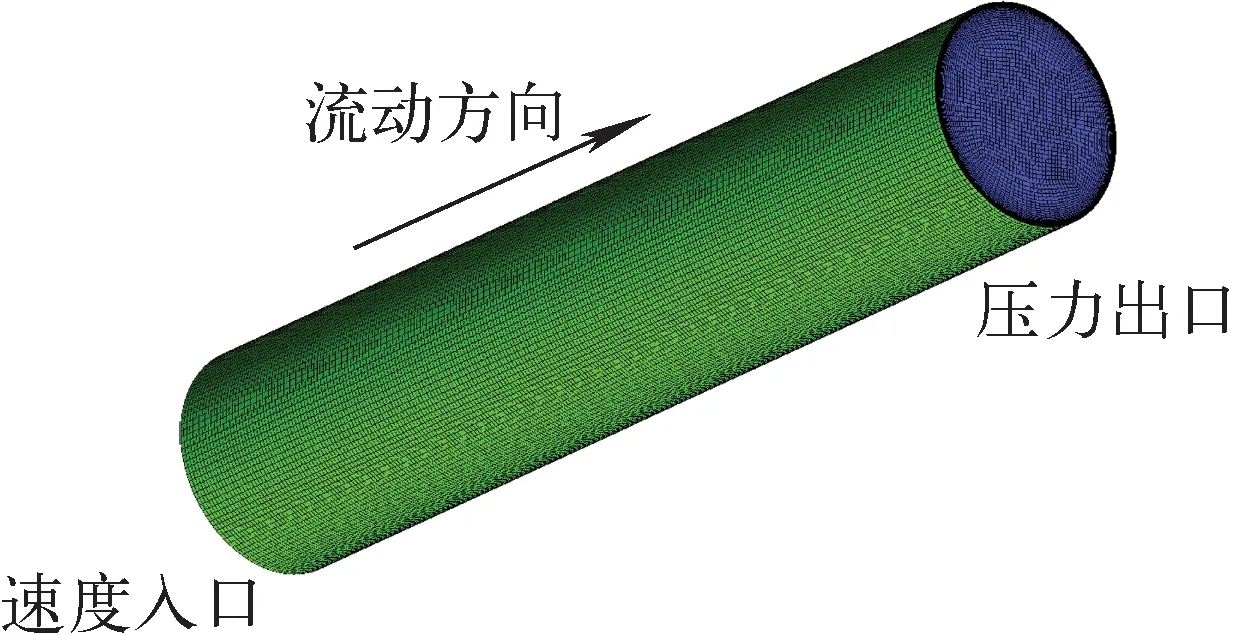
图4 实验段网格Fig.4 Mesh of experimental section

以分层床中小颗粒堆积层内的流动压降为参考，在流体入口表观流速为18 mm/s的情况下进行网格无关性检验，通过改变节点数量来改变网格数量，网格无关性检验结果如图5所示。图中，区域Ⅰ代表改变高度方向上节点数目的计算结果，区域Ⅱ代表改变横截面上节点数目的计算结果。需要说明的是，在网格无关性检验中，为准确获得流体在分层床沿高度方向上的流动压降特性，首先通过增加高度方向上的节点数目(区域Ⅰ)来增加网格数量，待分层床中小颗粒层的流动压降不随网格变化后，为准确获得分层床内的径向横流特性，通过增加横截面上网格节点数目进一步增加网格数量(区域Ⅱ)。从图5可看到，沿横截面加密网格会导致小颗粒层的压降突然增加(区域Ⅱ)。为验证横截面网格节点数量增加是否会影响高度方向上的网格无关性检验结果，在区域Ⅱ压力稳定后继续增加高度方向上的节点数目进行网格加密。可见，当网格数量大于18万时，无论从横截面方向还是从高度方向对网格进行加密，网格数量对计算结果的影响均较小。综合考虑计算精度和计算时间，最终采用214 200的网格进行计算。

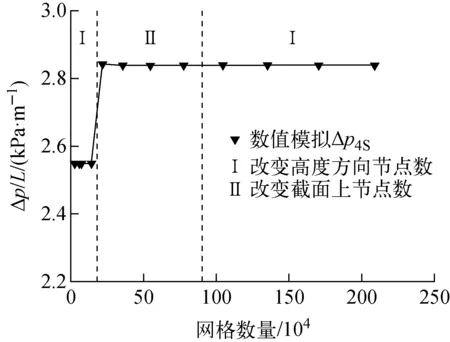
图5 压降随网格数量的变化Fig.5 Variation of pressure drop with number of mesh

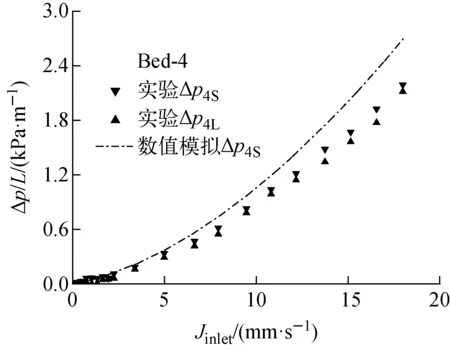
图6 实验及数值模拟流动压降随流体入口表观流速的变化Fig.6 Variation of flow pressure drop with superficial flowrate of experiment and numerical simulation

图6示出了分层床的小颗粒层中流动压降随流体入口表观流速变化的实验结果及数值模拟结果。从图6可看到，数值模拟计算相对误差随着流体流速的增加而增大。最大相对误差为18.7%，满足工业应用要求。

2.4 径向分层床内的二维流动现象

通过分析实验结果可推测，在径向分层床中，流体流量可能会发生再分配。图7示出了流体入口表观流速为18 mm/s时，分层床中径向横截面的速度矢量图。从图7可看到，在分层床入口段，流体流速除了存在竖直分量，还存在明显的水平分量，因此可说明分层床中存在流体流量再分配现象。

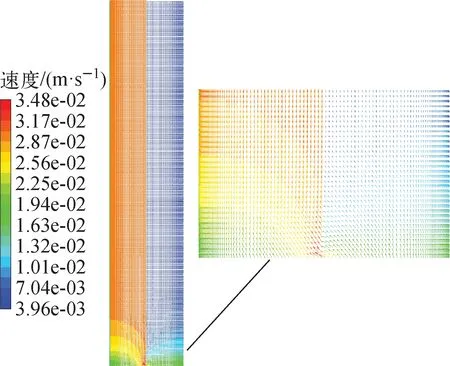
图7 分层床的径向横截面速度矢量图Fig. 7 Radial cross section velocity vector diagram of stratified bed

图8 加装挡板后分层床的径向横截面速度矢量图Fig.8 Radial cross section velocity vector diagram of stratified bed with baffle configuration

为排除入口效应的影响，在模型的两层分界面处增加了1个宽度为120 mm、高度为150 mm的挡板，防止流体在实验段入口发生横流，这种情况下，流体流量平均分布在两分层入口。图8为流体入口表观流速为18 mm/s时，安装挡板后分层床的径向横截面速度矢量图。从图8可看到，当床高小于150 mm时，两颗粒层中的流体流量相等，且流动均为一维竖直向上流动。当床高大于150 mm时，流体除了竖直向上流动，还有部分流体从小颗粒层流向大颗粒层，呈二维流动。分析认为，流体进入渗透率不同的分层颗粒堆积床后，由于两层的渗透率不同，导致部分流体由低渗透率的小颗粒层流向高渗透率的大颗粒层(横流)，促使流体在颗粒层内发生了流量的重新分配，导致小颗粒层内流体流量减少，流动压降降低；而大颗粒层内的流体流量增加，流动压降升高，最终分层床内两侧压降趋于平衡。这与图3中分层床内实验测量结果基本一致。

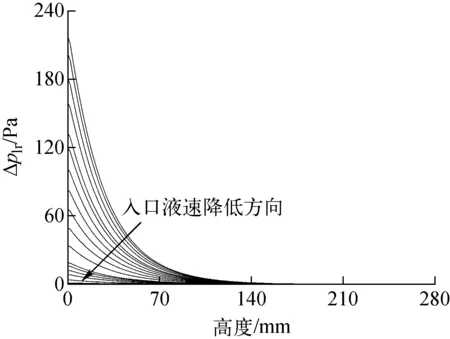
图9 径向分层床横向压降沿高度方向的变化Fig.9 Pressure difference between two layers of radial stratified bed along with bed height

由图7可进一步看出，横流仅发生在入口段较低的位置。分析认为，当流体进入径向分层床后，受堆积颗粒尺寸影响，小颗粒层内的压降将大于大颗粒层内压降，这导致同一高度下分层床左右分层内存在横向压差，部分流体将从小颗粒层流入到大颗粒层。随着横流的发生，小颗粒层内流体流量逐渐降低，大颗粒层内流体流量逐渐升高，两分层床内压降差异逐渐减小。当两分层内横向压差减小至0时，分层床内左右两侧压降达到平衡状态，此后沿分层床高度方向上不再发生横流。为研究横流发生的高度，图9示出了分层床小颗粒层和大颗粒层之间的横向压差(Δplr)沿分层床高度(h)的变化。图中不同的实线分别表示分层床中不同流体表观流速下的结果。

由图9可见，当床高低于150 mm时，分层床两分层的横向压差沿床高迅速减小；当床高大于150 mm时，横向压差为0。从某种意义上说，当床高小于150 mm时，横流流量沿分层床高度方向迅速减小，当床高度超过150 mm时，分层床内几乎不存在横向流动。基于该分析结果，可认为分层床内大部分横流流动仅发生在分层床的入口部分，现有工况条件下，仅发生在距离分层床入口高度150 mm范围内。

2.5 径向分层床内的横流流量特性

由2.3节分析可得，横流只发生在径向分层床入口段，为进一步研究横流发生的程度，采用式(12)计算累计横流分布百分比：

(12)

式中：Cn为不同高度下累计横流分布百分比；Qi为某一高度下分层界面处的横流流量，m3/s；Qtotal为分层界面处的横流总流量，m3/s。

图10为各流速下分层床中累计横流分布百分比沿分层床高度的变化。从图10可看到，随着分层床高度的增加，累计横流分布百分比迅速增加，且当分层床高度超过150 mm时，累计横流分布百分比达到99%，这进一步说明大部分横流发生在距离分层床入口150 mm范围内。

图10 累计横流分布百分比沿高度方向的变化Fig.10 Variation of cross flow cumulative distribution function along bed height

图11为分层床中平均横流流速(Jh)和横流流量占比(Ch)随入口表观流速的变化。其中，Jh代表分层床中模拟得到的横流流速在分层界面处的平均值，Ch代表分层床中横流流体体积流量与流体总体积流量之比。从图11可看到，整体上，随着流体入口表观流速的增加，分层床分层界面处的平均横流流速增加，但横流流量占比减小。分析认为，分层床两堆积层的横向压差随流体入口表观流速的增大而增大，从而导致横流流速随流体入口表观流速的增加而增大。

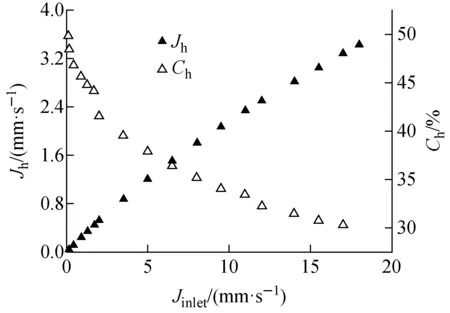
图11 径向分层床中平均横流流速和横流流量占比随流体入口表观流速的变化Fig.11 Variation of average lateral flowrate and cross flow ratio with superficial flowrate in radial stratified bed

3 结论

本文利用直径为2 mm和8 mm的玻璃圆球构建了2个单一尺寸颗粒堆积床、1个不同尺寸颗粒均匀混合堆积床和1个具有径向分层结构的颗粒堆积床，实验和数值模拟研究了颗粒堆积床内的流动压降特性，得到如下主要结论。

1) 对于均质床，3组床内的流动压降均随流体入口表观流速的增加而增大。对于径向分层床，两分层内流动压降相等。另外，分层床中小颗粒层对横流引起的压力变化更敏感。

2) 与均质床内的一维流动不同，在分层床中，由于分层床中左右两侧的渗透率不同，导致两分层内流动压降特性不同，引起流体从低渗透率层流向高渗透率层，流体在分层床中除了沿高度方向的流动，还存在沿径向的横流，出现了二维流动。二维流动主要发生在实验段初始部分(最大发生高度约为150 mm)。

3) 随着流体入口流量的增加，分层床分层界面处的平均横流流速逐渐增加，而横流流体体积流量与流体总体积流量之比逐渐减小。不同液体流量下，分层床的累计横流分布百分比几乎相同。