基于J-A模型的电工钢片磁致伸缩特性模拟与实验

李岱岩 张艳丽 荆 盈 王 振 张殿海

基于J-A模型的电工钢片磁致伸缩特性模拟与实验

李岱岩 张艳丽 荆 盈 王 振 张殿海

（沈阳工业大学电气工程学院 沈阳 110870）

电工钢片的磁致伸缩现象是引起电机、变压器铁心振动的一个重要原因。磁致伸缩特性与铁心的磁化方式密切相关。电机定子铁心存在大量旋转磁场，相比于交变磁化，旋转磁化会引起更大的磁致伸缩应变，准确模拟旋转磁化下电工钢片的磁致伸缩特性是实现电工产品性能优化的前提和基础。该文借鉴Jiles-Atherton（J-A）磁滞模型对磁化过程中磁畴畴壁移动和磁矩转动而产生滞后行为的表征方法，提出一种能够描述旋转磁化下磁致伸缩正应变和剪切应变矢量、滞后特性的磁致伸缩模型。基于电工钢片旋转磁特性测量系统提供的特性数据，采用粒子群优化算法实现了模型参数辨识，并验证了模型的准确性。制作并搭建硅钢叠片铁心局部磁致伸缩特性测量系统，给出了所提磁致伸缩模型计算铁心磁致伸缩形变的具体过程，通过与测量结果的比较，进一步分析了所提理论模型的有效性。研究表明，旋转磁化下电工钢片磁致伸缩具有滞后行为，该文从磁化机理角度提出的磁致伸缩模型可以有效地表征这种特性。

旋转磁化 磁致伸缩 电工钢片 J-A模型

0 引言

随着电工产品绿色、节能运行要求的不断提升，电工设备产生的振动噪声问题引起越来越多关注。电机、变压器铁心由电工钢片叠积而成，电工钢片的磁致伸缩效应（指磁性材料在周期性变化磁场中几何尺寸的微小变化）会加剧铁心的振动和噪声[1]。铁心的磁致伸缩特性与其工作中的磁感应强度大小、方向、频率等磁化方式密切相关。准确模拟电工钢片的磁致伸缩特性是研制高品质电工设备的前提和基础。

为了揭示磁致伸缩的物理本质，国内外学者基于不同的理论模型提出了模拟交变磁化下电工钢片磁致伸缩特性的方法。文献[2-3]基于Jiles-Atherton（J-A）磁滞理论，通过能量最低原理表征了发生在磁化方向的磁致伸缩应变特性。该模型只能模拟交变磁化的磁致伸缩应变，属于标量磁致伸缩模型。文献[4-5]基于亥姆霍兹自由能建立了标量磁致伸缩模型，该模型物理意义明确。但由于亥姆霍兹自由能函数无法准确获得，只能以多元函数的泰勒展开形式给出，展开后多项式的各项系数需要大量实验数据计算来获取。文献[6-7]基于神经网络法模拟了交变磁化下电工钢片的磁致伸缩各向异性特性。文献[8]基于硅钢中磁畴的旋转特性和J-A磁滞理论建立了取向电工钢片的标量磁致伸缩模型，并对交变谐波和直流偏磁下，取向电工钢片磁致伸缩特性进行了分析。文献[9]基于吉布斯自由能理论改进了考虑力-磁耦合效应的无取向电工钢片的标量磁致伸缩模型。

然而，除交变磁化外，电机定子铁心中同时存在旋转磁化，旋转磁化会产生更大的磁致伸缩应 变，且具有矢量特性[10]。近年来，国外学者率先基于自主研发的二维磁特性测量系统测试了旋转磁致伸缩特性，并提出了相应的模拟方法。日本学者M. Enokizono等对二维旋转磁化下电工钢片的磁滞特性和磁致伸缩特性进行了测量[11]。基于测量数据并类比E&S（Enokizono & Soda）模型提出了旋转磁化下ES-W（Enokizono & Soda-Wakabayashi）矢量磁致伸缩模型[12]，仿真计算了电机定子铁心的变形。ES-W基于实验数据拟合了旋转磁化下磁致伸缩主应变与磁通密度的关系。模型具有较好的精度，但模型参数较多、计算公式复杂，工程实用性有待提高。英国学者A. J. Moses[13]等基于旋转磁特性测量数据，类比机械弹性方程提出了一种旋转磁化下磁致伸缩矢量模型，该模型定义了磁杨氏模量、磁泊松比和磁剪切模量等参数，借助一阶惯性系统方程实现了对旋转磁致伸缩的模拟，但因为模型参数取为定值，无法反映旋转磁化轨迹的影响，限制了模型的计算精度。文献[14]基于轧制方向（Rolling Direction, RD）与垂直于轧制方向（Transverse Direction, TD）的磁致伸缩与磁通密度的测量数据，通过拟合两个方向上磁致伸缩与磁通密度的关系，建立了旋转磁化下的磁致伸缩模型。但是，单向磁化下的磁畴变化与二维旋转磁化下的磁畴变化完全不同，因此只能近似地使用RD和TD的磁致伸缩分量建立旋转磁致伸缩模型。国内针对电工钢片磁特性的研究主要集中在交变磁化及交变叠加谐波、直流偏磁、应力、温度等特性的测量和模拟[15-24]，而旋转磁化下磁致伸缩特性的分析和模拟研究正处于起步阶段，文献[25]基于ES-W模型表征了电工钢片的旋转磁致伸缩特性，但缺少对磁化现象的物理描述，模型参数过于依赖测量数据。

本文类比传统标量J-A磁滞模型对磁特性滞后行为的表述方法，从磁化理论出发提出一种旋转磁化下考虑磁致伸缩滞后效应的矢量磁致伸缩模型，模型中电工钢片平面磁致伸缩应变的两个正应变和一个剪切应变与旋转磁化轨迹密切相关。基于粒子群优化（Particle Swarm Optimization, PSO）算法对模型进行参数辨识，并制作了硅钢叠片局部磁致伸缩实验模型，通过与实验测试结果对比，验证所提模型的有效性。

1 基于J-A磁滞模型理论的旋转磁致伸缩应变特性模拟

1.1 传统J-A磁滞模型理论

磁性材料磁化过程伴随着磁畴的两种变动，即磁畴间畴壁的位移和磁畴内磁矩的转动。磁畴在磁化过程中要克服材料存在的杂质、空穴或因材料不均匀性产生的内应力等引起的钉扎效应，钉扎对磁畴移动的阻碍是造成磁滞现象和产生不可逆磁化的主要原因。基于这一磁化理论[26]，J-A磁滞模型将磁化强度分为可逆磁化分量与不可逆磁化分量两部分，即

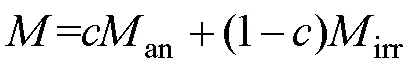
式中，为可逆磁化系数；an为理想的无磁滞磁化下的磁化强度，是可逆磁化分量；irr为不可逆磁化分量，通常用一阶常微分方程描述磁特性的滞后行为与不可逆性[27-28]，其表达式为

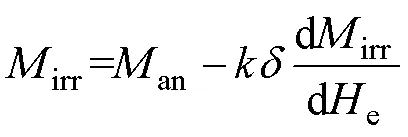
其中

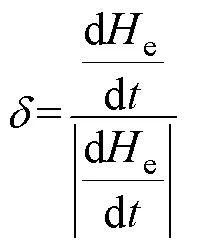
式中，为钉扎常数，与irr对e的一阶导数项共同描述了磁滞行为，即磁滞回环的形状；描述了磁化过程中的不可逆行为；e为有效磁场强度；为外磁场强度；为磁畴间耦合的平均场系数。

1.2 基于J-A磁滞模型理论的旋转磁致伸缩应变模拟

对于硅钢材料，磁致伸缩应变数量级为每米几微米或几十微米。磁化过程磁畴的移动、磁矩的转动也引起了磁性材料的磁致伸缩现象。交变磁化下，磁致伸缩与磁化强度在静态（不考虑磁致伸缩动态回环）且不考虑饱和的情况下通常可表示为二次方关系[11]，即

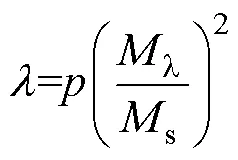
式中，Ms为饱和磁化强度；Ml 为磁畴畴壁移动和磁矩转动时引起磁致伸缩应变的磁化强度；p为待定系数，描述式（3）的抛物线函数的起始特性。然而，实际上一个交变磁化周期下磁致伸缩与磁化强度（或磁通密度）的动态关系曲线为动态回环（通常称为蝴蝶曲线），如图1所示[29]，磁致伸缩l 变化滞后于M（或B）的变化。

与磁滞回环的滞后类似，磁致伸缩的滞后行为也是由钉扎作用引起，为此，类比式（1），本文将引起磁致伸缩效应的磁化强度表达为

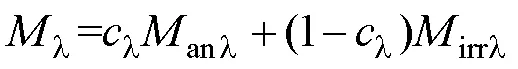
式中，anl为引起无滞后磁致伸缩行为的磁化强度；irrl为引起磁致伸缩的不可逆磁化分量，文献[30]指出磁致伸缩的不可逆磁化分量主要由与磁化方向夹角不为0°的畴壁位移产生；l为引起磁致伸缩的可逆磁化系数。于是，有

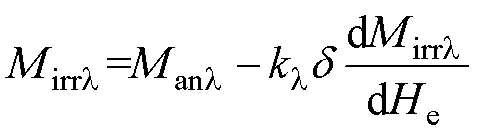
式中，l为磁致伸缩钉扎常数；l与irrl对e的一阶导数项共同描述磁致伸缩的滞后行为，即磁致伸缩动态回环。

将式（4）和式（5）代入式（3），将磁致伸缩应变表示为磁化强度的函数，得到交变磁化下描述磁致伸缩动态滞后行为的标量模型为

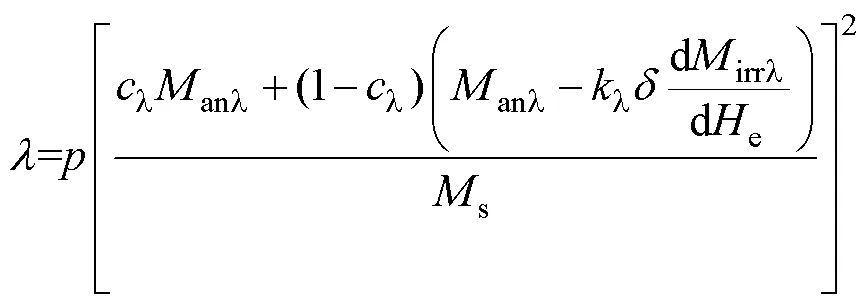
根据材料力学知识，平面应变包含两个正应变和一个剪切应变。为了模拟旋转磁化下的平面磁致伸缩应变特性，基于式（6），本文提出将平面磁致伸缩应变的3个分量表示为

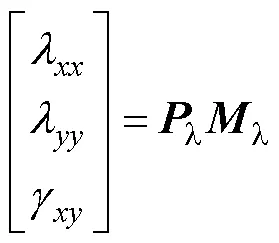
式中，、和分别为磁致伸缩在和两个正交方向的正应变和两个方向之间的剪切应变，本文取方向为电工钢片的轧制方向，方向为垂直于轧制方向；l定义为3×3系数矩阵，矩阵元素用于反映旋转磁化过程中磁化强度（或磁通密度）矢量在一个磁化周期内大小和方向的变化规律，后文详细介绍该系数矩阵的参数辨识过程。

式（7）中，l为磁化强度矢量，具体为

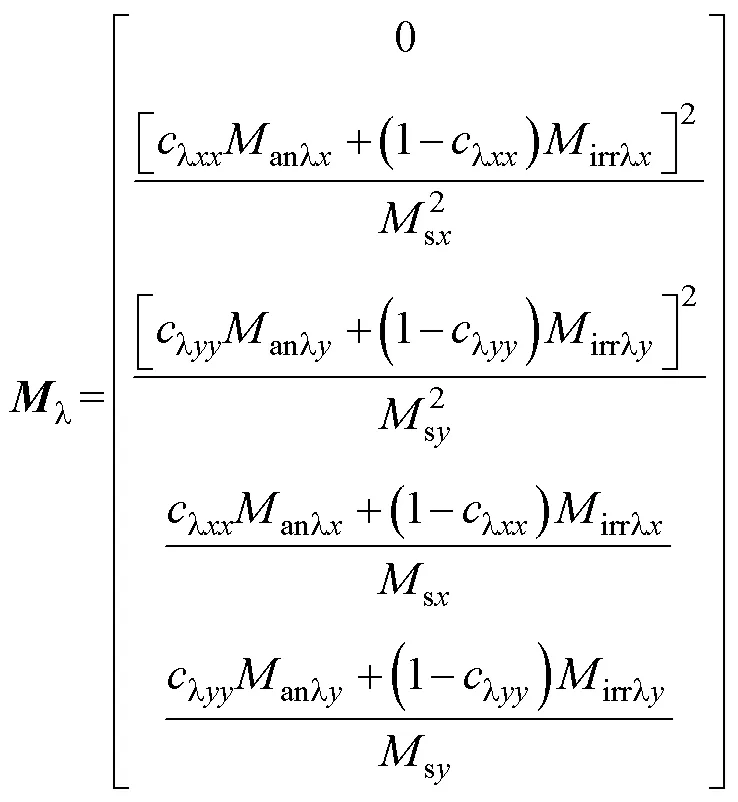
其中

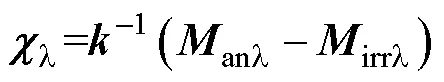
式中，sx和sy分别为饱和磁化强度的、分量；anl、irrl和e分别为引起无滞后磁致伸缩行为的磁化强度、引起磁致伸缩的不可逆磁化分量和有效磁场的矢量形式；为代表RD与TD钉扎常数的对角张量，包括lxx和lyy两个值，均为待定参数；lxx、lyy为待定的可逆磁化系数。这些待定参数需要通过RD和TD方向的磁致伸缩动态回环进行辨识，具体过程见第2节。

式（7）表征了旋转磁化下电工钢片平面磁致伸缩应变的矢量、滞后特性，同时，通过系数矩阵l进一步体现旋转磁化轨迹的影响。

2 模型参数辨识

2.1 旋转磁致伸缩特性分析

单片电工钢片旋转磁致伸缩测量系统如图2所示[21]。该装置通过闭环负反馈调节，实现了被测样片内磁通密度对给定的波形的跟踪；磁致伸缩的测量是通过三轴应变片实现的。具体原理已在文献[24]中详细介绍，本文不再赘述。

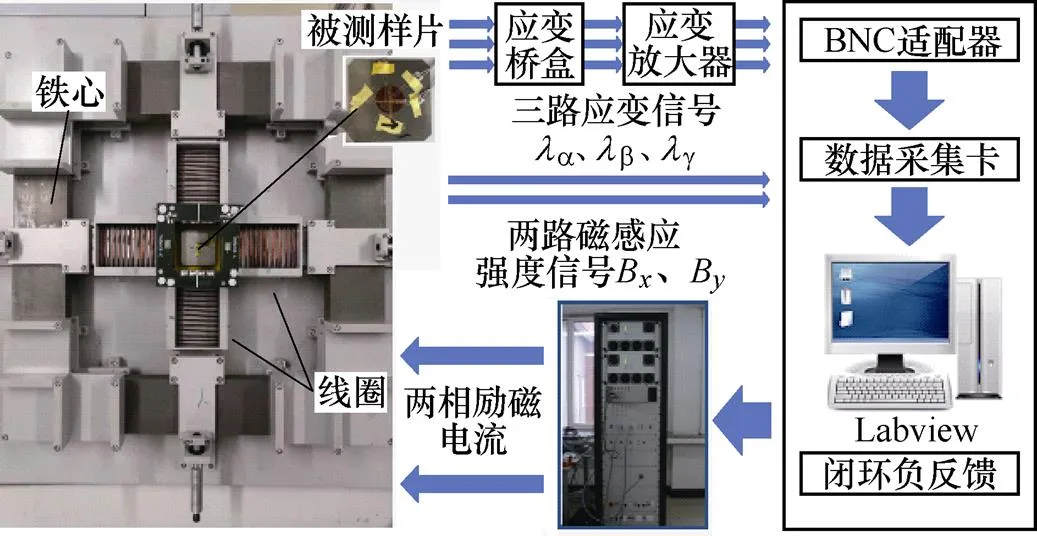
图2 旋转磁致伸缩特性测量系统

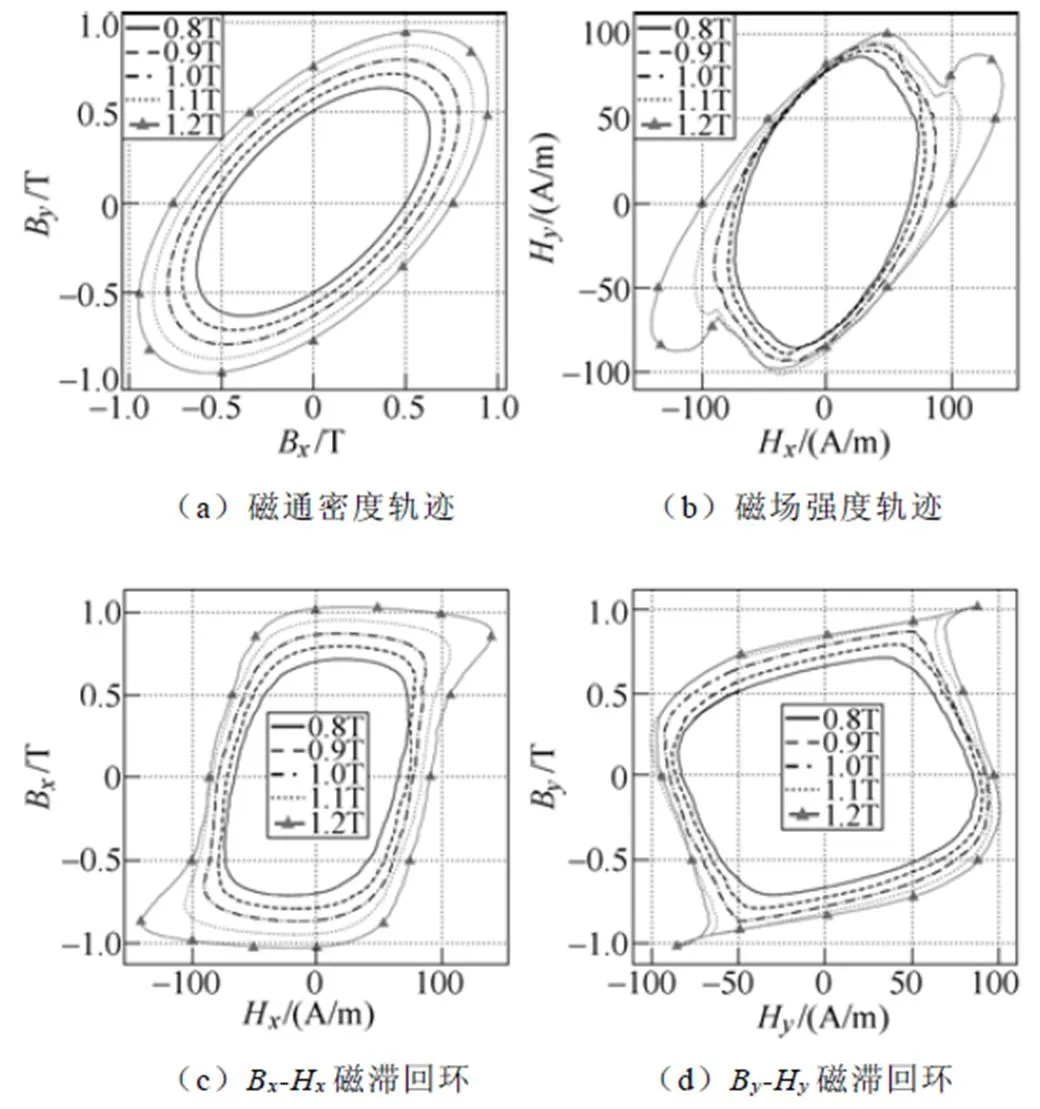
测量过程中，旋转磁化下功率放大器提供的电源励磁频率为50Hz；一个磁化周期内磁通密度矢量按照椭圆形轨迹旋转，椭圆的长轴max变化范围0.5～1.7T，间隔为0.1T；轴比由0～1.0变化，间隔为0.2；B由0°～90°变化，间隔为15°。图3为旋转磁化轨迹为 =0.5、B=45°时一个周期内max由0.8～1.2T变化、间隔0.1T的磁滞回环、磁致伸缩回环的测量结果。

由图3可以看出，在不同旋转磁化轨迹下，-磁致伸缩回环与-磁滞回环均表现为动态的、各向异性的滞后特性，反映了磁化过程中钉扎效应对磁畴移动的阻碍引起的不可逆磁化现象，同时这两种回环的相似特性也说明了本文用类比磁滞模型推演磁致伸缩模型的可行性。

2.2 磁致伸缩模型参数辨识

参数辨识是建模的重要部分，本文利用PSO对式（7）、式（8）中的参数进行辨识。参数辨识的数据来自2.1节的实验测量结果，旋转磁通轨迹变化范围是：max为0.5～1.7T，步长为0.1T；轴比为0～1，间隔0.2；磁化角度B为0°～90°，步长为15°，共计13×6×7=546种旋转磁化轨迹。模型式（7）中磁致伸缩两个正应变和一个剪切应变由三轴应变计测量得到，对应于不同的旋转磁化轨迹。寻优过程中，将参数l、l和l、l或l、l、l、l和g作为待优化变量，采用方差作为目标（适应度）函数，表达式为

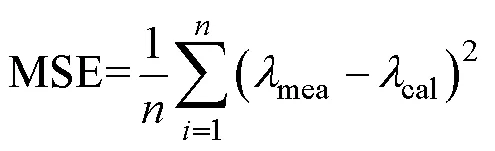
式中，为一个磁化周期内采样的离散点的数量；cal为式（7）计算得到的磁致伸缩应变计算值；mea为磁致伸缩的测量结果。特别地，对l、l和l、l这组参数进行寻优时，cal为RD和TD方向磁致伸缩应变的计算值，mea为测量值。对l、l、l、l和g这一组参数进行寻优时，cal则为平面磁致伸缩应变张量的计算值，即、和；mea为平面磁致伸缩应变张量的测量值。

粒子群算法执行过程如图4所示。参数寻优过程如下：设置最大迭代次数为200；初始化粒子群，设粒子个数为50个；初始化粒子运动速度；初始化粒子运动惯性系数；设置粒子加速度常数1和2。每次迭代时每个粒子的速度更新与位置更新公式分别为

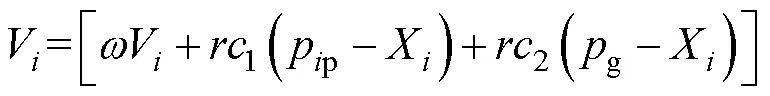
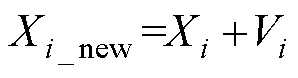
式中，为每次迭代的粒子序号；为一个（0, 1）的随机实数；pp为粒子在当前迭代次数中的最优解；g为全局最优解；为惯性系数，为一个（0, 1）的实数，其值影响粒子群的局部寻优和全局寻优能力，当较大时，粒子群的全局寻优能力较强，当较小时，粒子群的局部寻优能力较强；X为粒子当前位置；X_new为粒子在本次迭代后更新后的位置。基于此，本文采用变惯性系数寻优，计算公式为

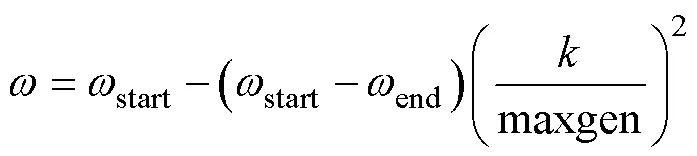
式中，start为初始的惯性系数；end为最终的惯性系数；为迭代次数；maxgen为最大迭代次数。在循环初期，利用式（12）计算得到较大的值，可以保证在全局范围内寻优。随着循环次数的增加，寻优过程基本已经确定最优解所在区域，此时式（12）将给出较小的值，进行局部寻优，加快寻优进程。经多次尝试，本文建议式（12）中start和end分别取为0.9和0.4。

对式（8）中的参数lxx、lyy和lxx、lyy进行辨识，确定磁致伸缩对磁化强度的滞后性。用到的旋转磁化轨迹为：max范围0.5～1.7T；轴比 =0；B=0°。辨识结果见表1。

表1lxx、lyy和lxx、lyy辨识结果

Tab.1 The values of klxx、klyyandclxx、clyy

基于不同旋转磁化轨迹下的磁致伸缩测量数据，利用粒子群优化算法对式（7）中系数矩阵l的各个参数值进行寻优。图5列举了在 =0.8、B= 45°以及max=0.9T的磁化轨迹下，参数lxx、lyy、lxx、lyy和gxy的收敛过程。

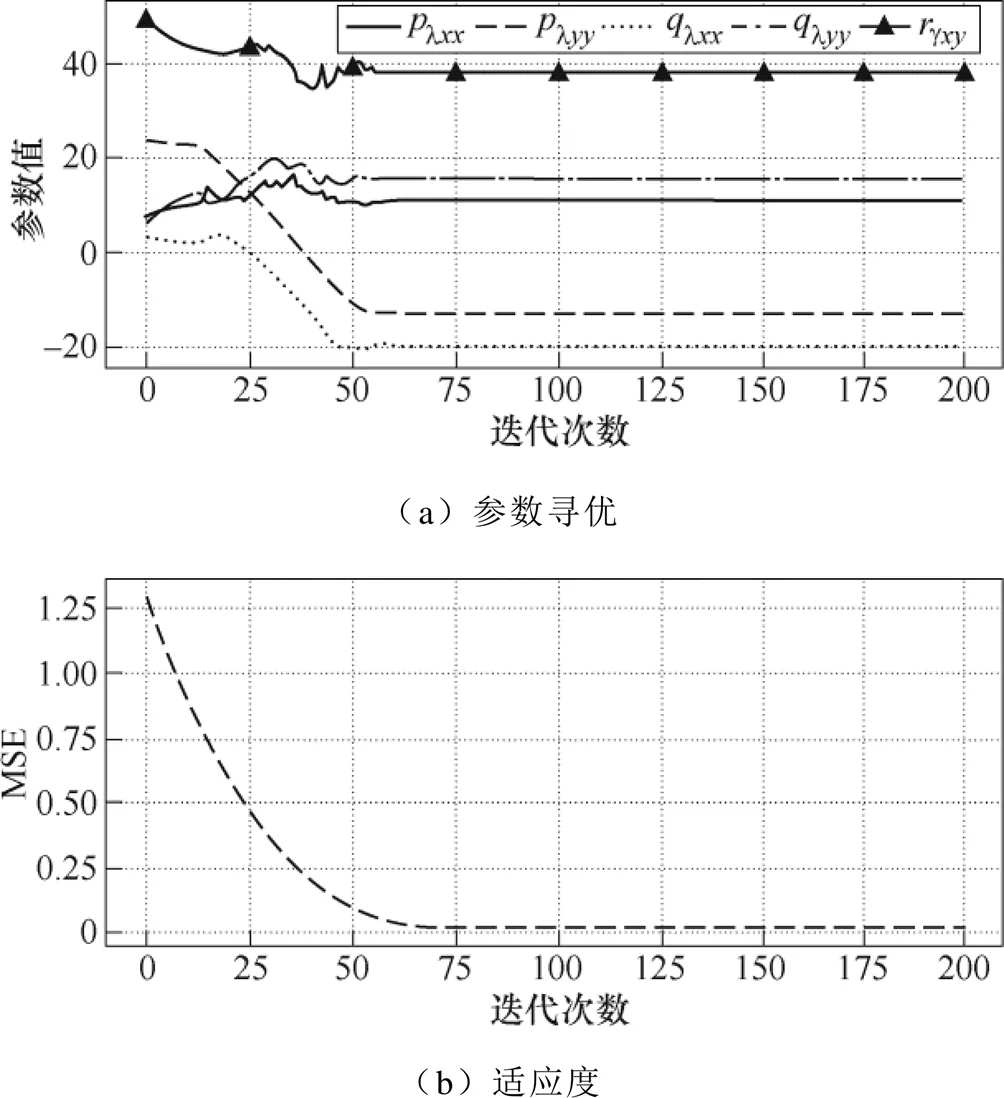
图5 待寻优参数收敛过程

参数lxx、lyy、lxx、lyy和gxy的值与旋转磁化轨迹有关，表2～表4列出了在部分旋转磁化轨迹下，lxx、lyy、lxx、lyy和gxy的值。

图6以曲面数据库的形式展示了更为全面的参数lxx、lyy、lxx、lyy和gxy的辨识结果。

表2 不同轴比下l、l、l、l、g值（max=0.9T、B=45°）

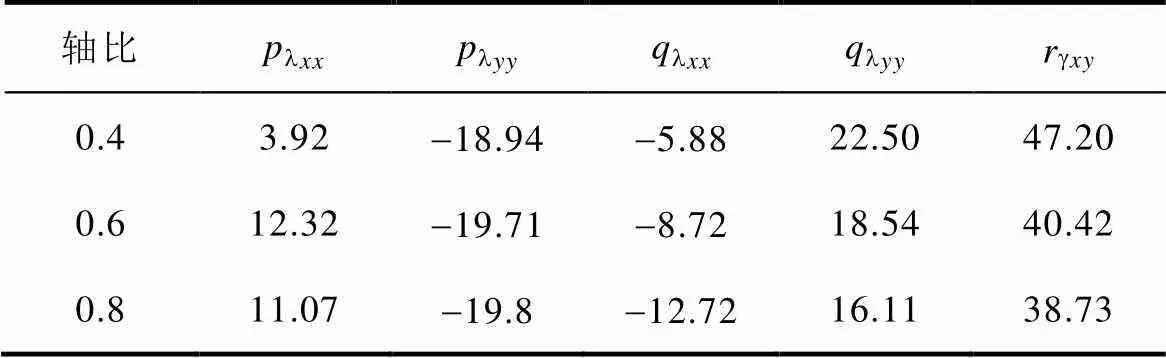
Tab.2 The values of plxx、plyy、qlxx、qlyy andrgxy under different a (Bmax=0.9T、qB=45°)

表3 不同磁化倾角下lxx、lyy、lxx、lyy、gxy值（max=1.2T、 =0.4）

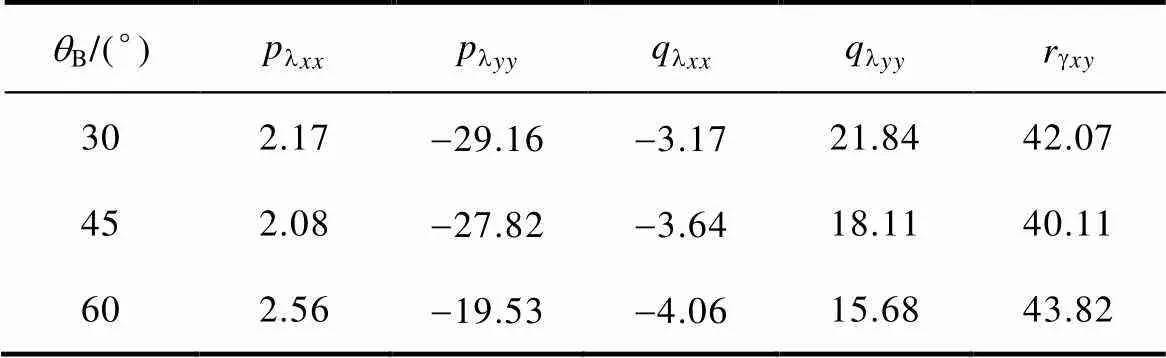
Tab.3 The values of plxx、plyy、qlxx、qlyy andrgxy under different qB (Bmax=1.2T、a =0.4)

表4 不同max下lxx、lyy、lxx、lyy、gxy值（B=30°、 =0.6）

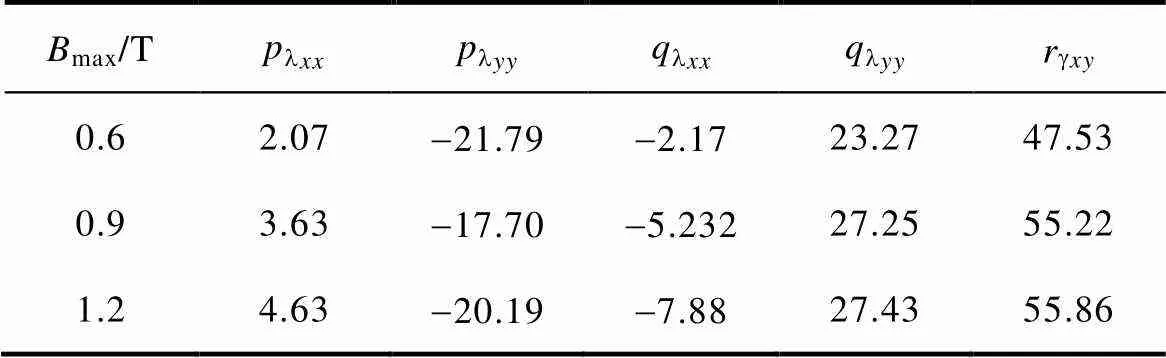
Tab.4 The values of plxx、plyy、qlxx、qlyy andrgxy under different Bmax (qB=30°、a =0.6)

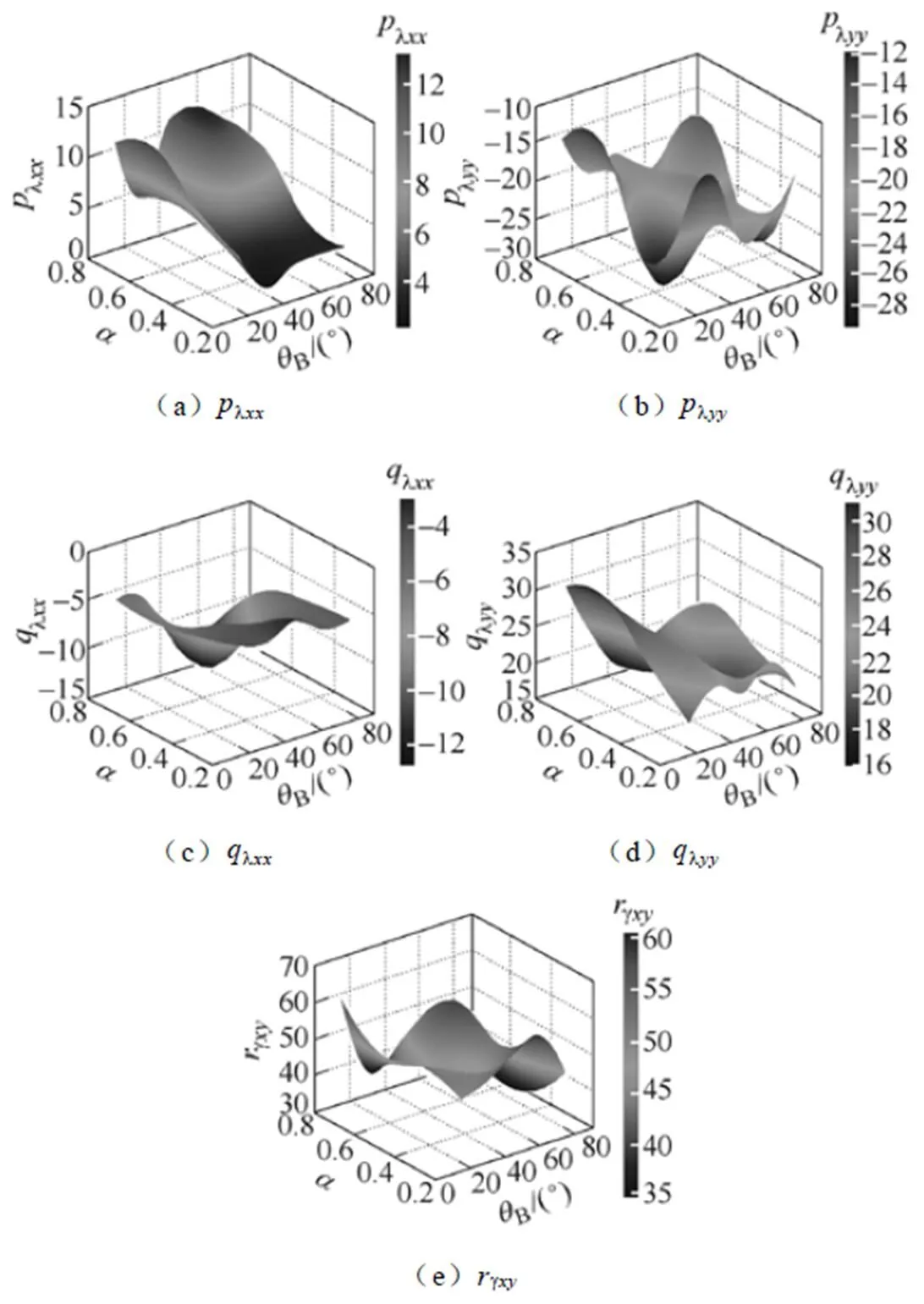
图6 plxx、plyy、qlxx、qlyy和rgxy辨识结果

2.3 模型验证

为了检验参数辨识的效果，本文对max=1.0T和max=1.6T（ =0.5、B=45°）两种不同磁通密度幅值的旋转磁化轨迹模型计算结果和测量结果进行了对比，对比结果如图7和图8所示。

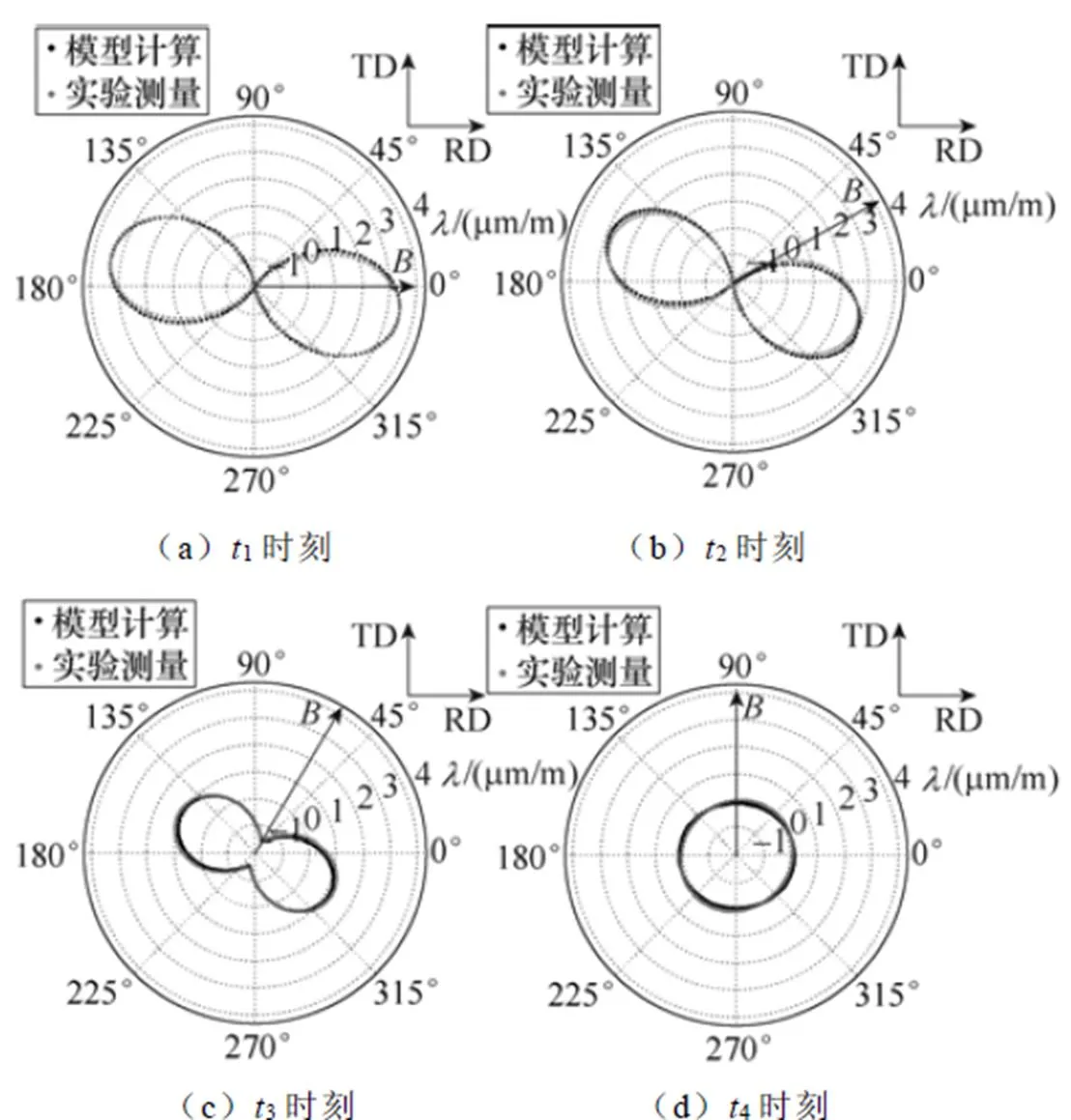
图7 旋转磁化下磁致伸缩应变计算值与测量值对比（Bmax=1.0T）

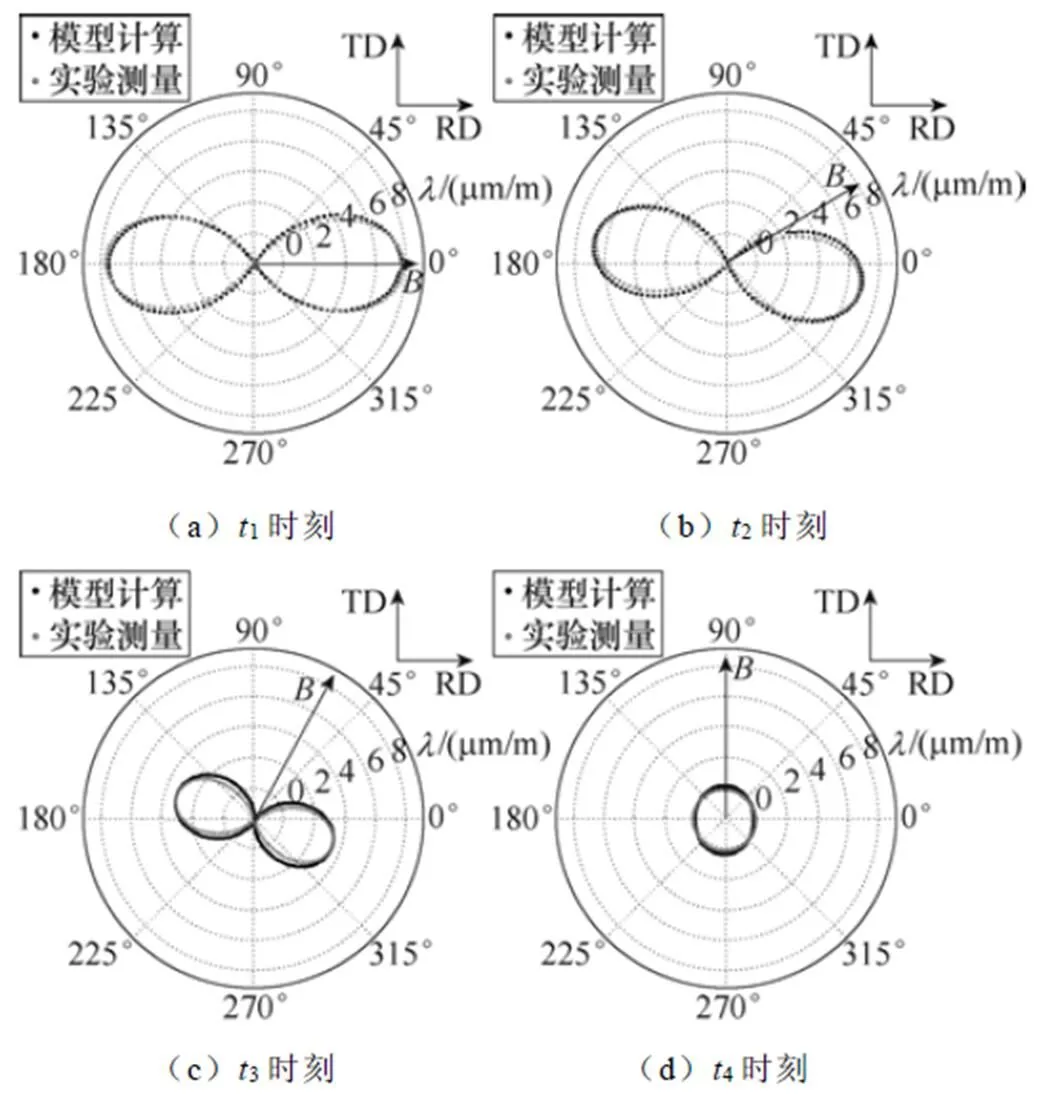
图8 旋转磁化下磁致伸缩应变计算值与测量值对比（Bmax=1.6T）

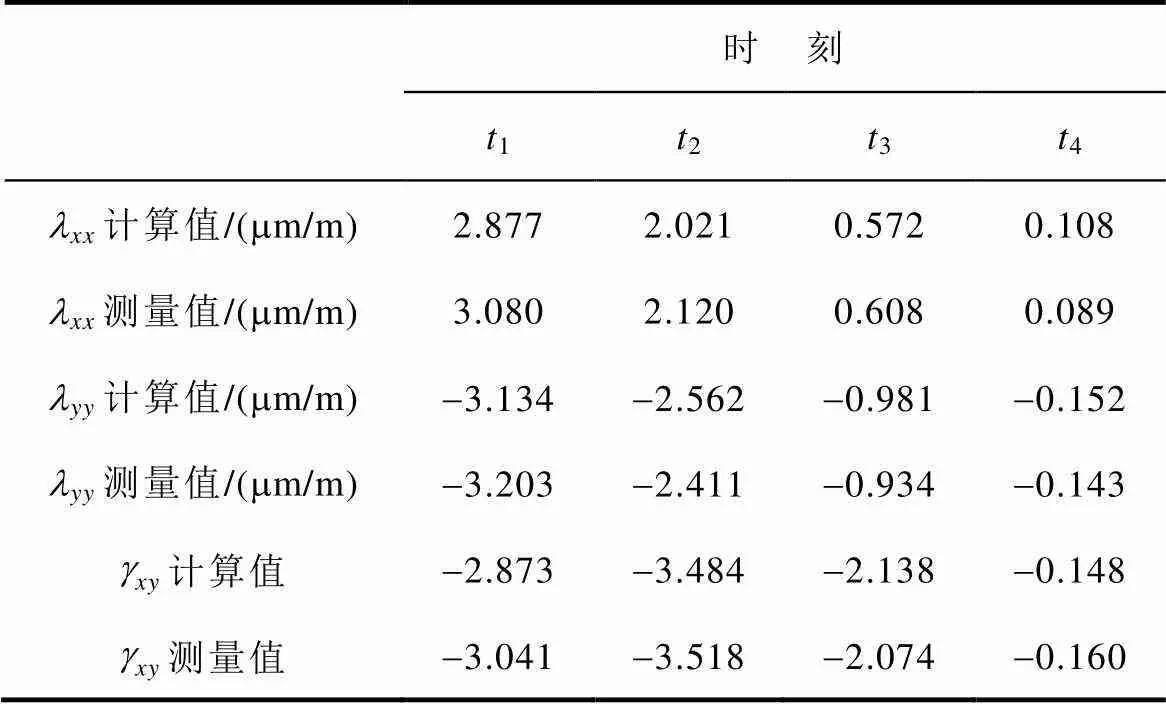
从图7和图8可以看出，模型计算得到的旋转轨迹与测量轨迹有很好的吻合性。为了进一步分析两者的对比情况，表5和表6列举了不同时刻旋转磁致伸缩应变的数值。表5中模型计算值和测量值的平均相对误差为5.88%；表6平均相对误差为6.92%。

表5、和的模型计算值与实验测量值的对比（max=1.0T、 =0.5、B=45°）

Tab.5 Comparison of the calculated values of the lxx, lyy and gxy models with the experimental measured values (Bmax=1.0T、a =0.5、qB=45°)

表6、和的模型计算值与实验测量值的对比（max=1.6T、 =0.5、B=45°）

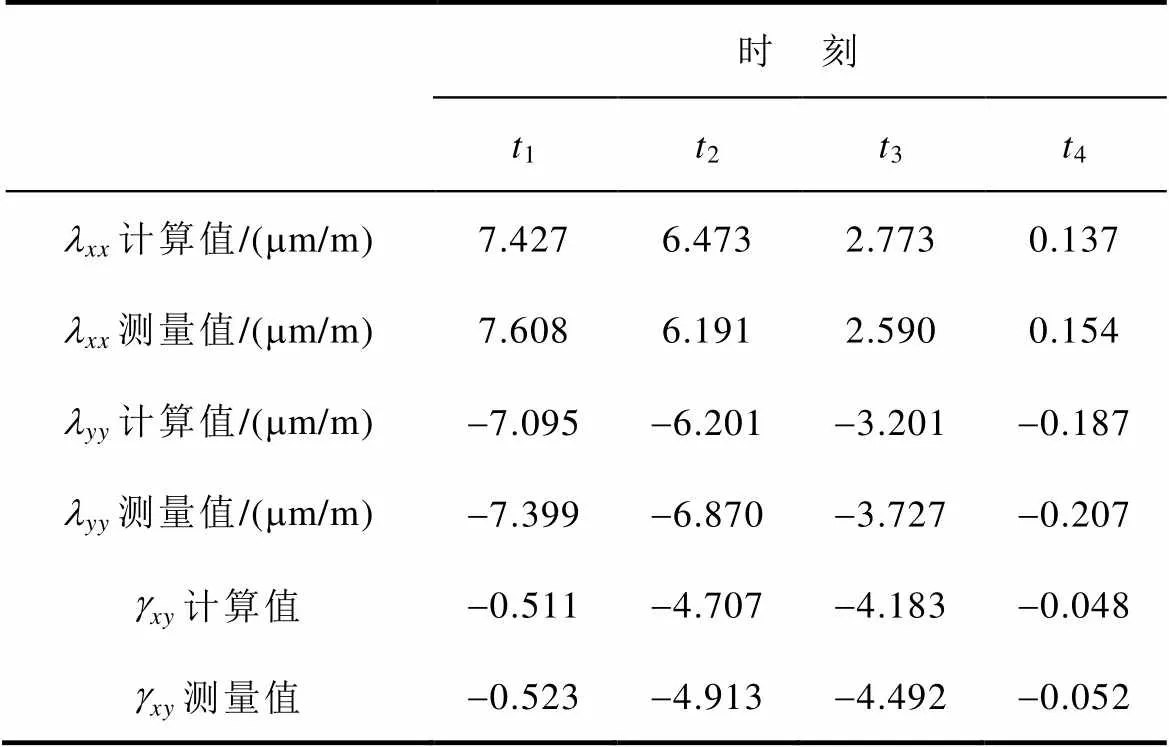
Tab.6 Comparison of the calculated values of the lxx, lyy and gxy models with the experimental measured values (Bmax=1.6T、a =0.5、qB=45°)

可以看出，模型计算值与实验测量值吻合度很好，验证了本文所提模型对不同磁通密度幅值的标准椭圆旋转磁化轨迹下磁致伸缩动态特性的模拟精度，所采用的粒子群算法能够有效地辨识模型参数。

3 模型在叠片铁心磁致伸缩应变计算中的应用与实验验证

将三相调压器输出端接铁心模型，调节调压器旋钮，即可以通过调节电压对磁场进行开环控制。通过B探头检测被测点的B、感应电压信号，B探头两个针脚相距9mm，测量误差低于0.25%[31]；通过三轴应变片测量被测点的磁致伸缩应变信号。检测到的信号再通过数据采集卡传送到上位机处理，检测系统如图10所示。

被测点选择在定子铁心的齿根部位，测得的磁感应强度轨迹如图10a所示，被测点在一个磁化周期任意选取4个时刻，图10给出了磁致伸缩应变在任意方向分布的计算结果与测量结果的对比情况。采用第2节所提矢量磁致伸缩模型计算铁心磁致伸缩应变的过程为：首先，进行铁心磁场仿真计算的建模和求解，得到铁心所有剖分单元磁通密度矢量在一个励磁周期的变化波形；然后，计算每个剖分单元中磁通密度变化轨迹的3个分量max和B，在模型参数辨识结果数据库中查取对应的模型参数值；最后，利用式（7）、式（8）计算铁心所有剖分单元的磁致伸缩应变的两个正应变和一个剪切应变，得到铁心不同位置的磁致伸缩应变分布。被测点不同时刻不同方向磁致伸缩应变计算值与测量值对比如图11所示。图11中，用箭头标出了对应时刻磁通密度矢量的方向。

图10 电机铁心局部磁致伸缩特性实验模型数据采集系统

从图11可以看出，模型的计算结果可以反映出铁心旋转磁致伸缩具有的矢量特性和滞后行为，并且与实验测量结果较为吻合。误差产生的原因分析如下：图8a测得的磁化轨迹是非标准的椭圆形状，与单片电工钢片旋转磁致伸缩测量时控制样片磁场为椭圆形轨迹不同，这是因为铁心是采用电压源且开环激励，以及电工钢片磁导率的非线性，所以会存在谐波成分。而计算模型是基于标准椭圆轨迹得到的，这也解释了计算值与测量值出现的差异。此外，被测点检测到的应变值也包含了电磁力引起的应变，尽管在测量结果中减去该部分值的影响（该值的确定方法是使用有限元方法计算了对应时刻下该点电磁力产生的应变），但仿真计算误差的存在也是图11误差出现的次要原因。

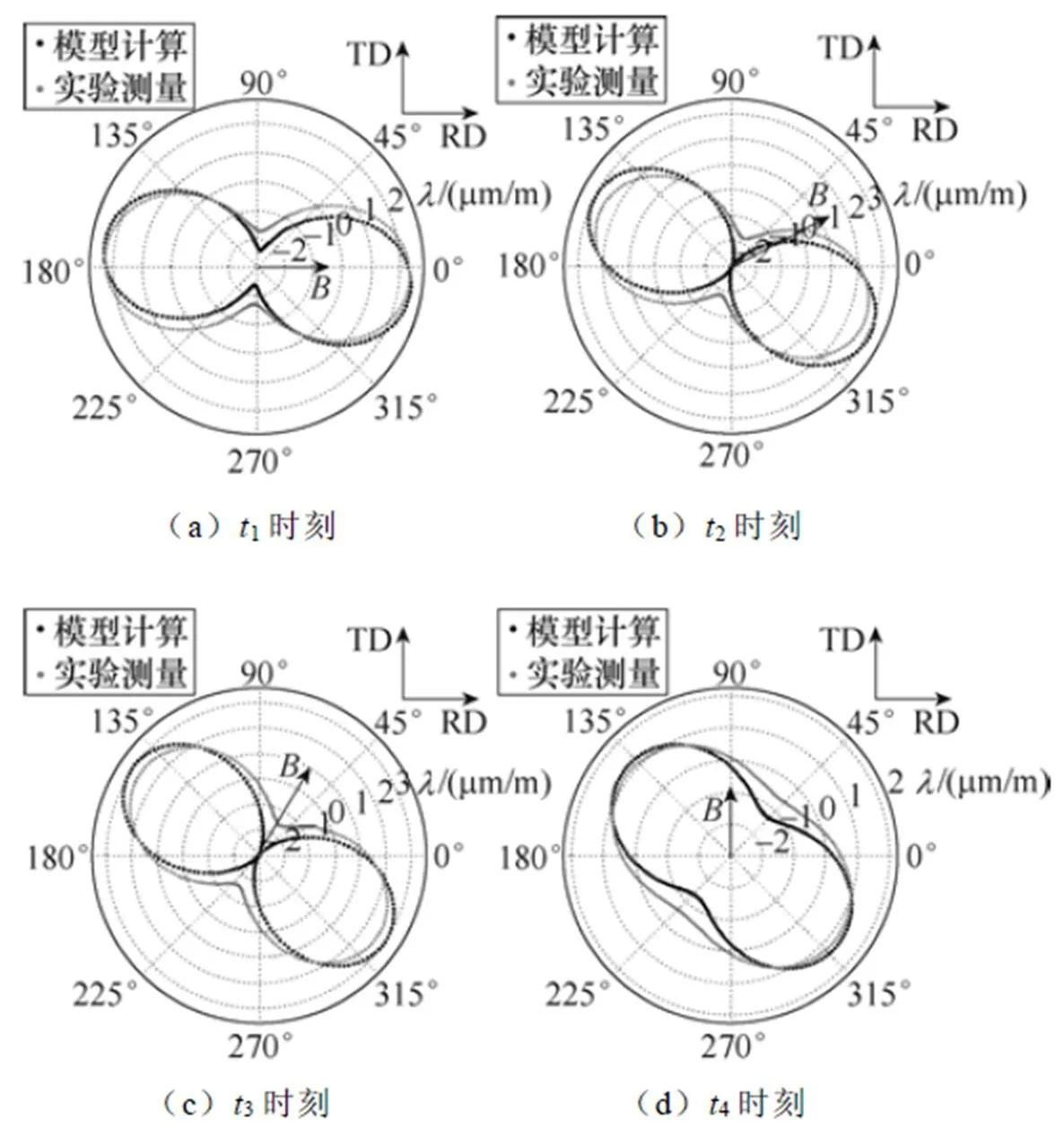
图11 被测点不同时刻不同方向磁致伸缩应变计算值与测量值对比

4 结论

本文基于旋转磁致伸缩测量系统，测量了旋转磁化下电工钢片的动态磁致伸缩特性。基于磁化理论、J-A模型理论和旋转磁致伸缩特性测量数据，提出了能够描述旋转磁化下磁致伸缩平面正应变和剪切应变的矢量磁致伸缩模型。采用粒子群优化算法对模型参数进行了辨识，并进行了模型验证。最后计算分析了该模型电机定子铁心的局部磁致伸缩应变，并与实验测量结果进行对比分析。得到结论如下：

1）对电工钢片旋转磁致伸缩的测量结果表明，旋转磁致伸缩具有复杂的动态特性、矢量特性和各向异性特性。与磁滞类似，磁致伸缩两个正应变分量分别与、方向的磁通密度在动态下呈现回环（蝴蝶曲线）的特性关系。

2）所提出的矢量磁致伸缩模型不仅能表征旋转磁化下磁致伸缩的矢量、滞后行为，还能通过模型参数模拟旋转磁化轨迹的变化特征。

3）对电机铁心磁致伸缩应变的测量结果验证了所提模型在工程应用的有效性，可以有效表征电工钢片旋转磁致伸缩特性。

上述研究成果提供了电工钢片旋转磁致伸缩特性的参考数据和测试手段，建立的特性模型也推动磁致伸缩表征方法向铁心服役工况靠近，为电机等电工装备本体振动噪声的研究提供了一定的参考。

[1] Somkun S, Moses A J, Anderson P I. Effect of magnetostriction anisotropy in nonoriented electrical steels on deformation of induction motor stator cores[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4744-4747.

[2] Sablik M J, Jiles D C. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis[J]. IEEE Transactions on Magnetics, 1993, 29(4): 2113-2123.

[3] Rasilo P, Singh D, Belahcen A, et al. Iron losses, magnetoelasticity and magnetostriction in ferromagnetic steel laminations[J]. IEEE Transactions on Magnetics, 2013, 49(5): 2041-2044.

[4] Belahcen A, Fonteyn K, Fortion S, et al. A coupled magnetoelastic model for ferromagnetic materials[J]. IEEE Transactions on Magnetics, 2008, 40(4): 1810- 1819.

[5] Fonteyn K, Belahcen A, Kouhia R, et al. FEM for directly coupled magneto-mechanical phenomena in electrical machines[J]. IEEE Transactions on Mag- netics, 2010, 46(8): 2923-2926.

[6] Wang Zhen, Zhang Yanli, Ren Ziyan, et al. Modeling of anisotropic magnetostriction under DC bias based on an optimized BP neural network[J]. IEEE Transa- ctions on Magnetics, 2020, 56(3): 1-4.

[7] Zhou Hang, Zhang Yanli, Zhang Dianhai, et al. An anisotropic magnetostriction model based on BP neural network combining Levenberg-Marquardt algorithm and particle swarm optimization[J]. International Journal of Applied Electromagnetics and Mechanics, 2017, 55: 193-201.

[8] 祝丽花, 李晶晶, 朱建国. 服役条件下取向硅钢磁致伸缩模型的研究[J]. 电工技术学报, 2020, 35(19): 4131-4138.

Zhu Lihua, Li Jingjing, Zhu Jianguo. Research on magnetostrictive model for oriented silicon steel under service conditions[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4131-4138.

[9] 贲彤, 陈芳媛, 陈龙, 等. 考虑力-磁耦合效应的无取向电工钢片磁致伸缩模型的改进[J]. 中国电机工程学报, 2021, 41(15): 5361-5371.

Ben Tong, Chen Fangyuan, Chen Long, et al. An improved magnetostrictive model of non-oriented electrical steel sheet considering force-magnetic coupling effect[J]. Proceedings of the CSEE, 2021, 41(15): 5361-5371.

[10] 李强. 基于三轴应变片测量的电工钢片矢量磁致伸缩特性研究[D]. 沈阳: 沈阳工业大学, 2016.

[11] Yamagashira M, Wakabayashi D, Enokizono M. Vector magnetic properties and 2-D magnetostriction of various electrical steel sheets under rotating flux condition[J]. IEEE Transactions on Magnetics, 2014, 50(4): 1-4.

[12] Wakabayashi D, Enokizono M. Two-dimensional magnetostriction analysis using E&S-W model in induction motor model core[C]//International Con- ference on Electrical Machines (ICEM), Berlin, Germany, 2014: 1468-1474.

[13] Somkun S, Moses A J, Anderson P I. Measurement and modeling of 2-D magnetostriction of nonoriented electrical steel[J]. IEEE Transactions on Magnetics, 2012, 48(2): 711-714.

[14] Belahcen A. Vibrations of rotating electrical machines due to magnetomechanical coupling and magnetostriction[J]. IEEE Transactions on Magnetics, 2006, 42(4): 971-974.

[15] 张黎, 王国政, 董攀婷, 等. 基于磁致伸缩本征特性的晶粒取向性变压器铁心振动模型[J]. 中国电机工程学报, 2016, 36(14): 3990-4001.

Zhang Li, Wang Guozheng, Dong Panting, et al. Study on the vibration of grain-oriented transformer core based on the magnetostrictive intrinsic characte- ristics[J]. Proceedings of the CSEE, 2016, 36(14): 3990-4001.

[16] 王佳音, 白保东, 刘宏亮, 等. 直流偏磁对变压器振动噪声的影响[J]. 电工技术学报, 2015, 30(8): 56-61.

Wang Jiayin, Bai Baodong, Liu Hongliang, et al. Research on vibration and noise of transformers under DC bias[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 56-61.

[17] Zhang Yanli, Wang Jiayin, Sun Xiaoguang, et al. Measurement and modeling of anisotropic mag- netostriction characteristic of grain-oriented silicon steel sheet under DC bias[J]. IEEE Transactions on Magnetics, 2014, 50(2): 361-364.

[18] 祝丽花, 石永恒, 杨庆新. 夹紧力对非晶合金磁特性及铁芯振动的影响研究[J]. 中国电机工程学报, 2020, 40(24): 8155-8164, 8252.

Zhu Lihua, Shi Yongheng, Yang Qingxin. Effect of clamping force on magnetic properties and core vibration of amorphous alloys[J]. Proceedings of the CSEE, 2020, 40(24): 8155-8164, 8252.

[19] Zhao Xiaojun, Du Yutong, Liu Yang, et al. Mag- netostrictive properties of the grain-oriented silicon steel sheet under DC-biased and multisinusoidal magnetizations[J]. Materials (Basel, Switzerland), 2019, 12(13): 2156-2170.

[20] 陈德志, 张玉庸, 白保东, 等. 不同温度及谐波下硅钢片电磁-力特性与变频电机振动[J]. 电工技术学报, 2020, 35(22): 4647-4656.

Chen Dezhi, Zhang Yuyong, Bai Baodong, et al. Electromagnetic-force and vibration of silicon steel sheetand variable frequency motor under different temperature and harmonic[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4647-4656.

[21] 张艳丽, 李强, 王洋洋, 等. 谐波磁场下硅钢片磁致伸缩特性分析[J]. 电工技术学报, 2015, 30(14): 545-550.

Zhang Yanli, Li Qiang, Wang Yangyang, et al. Analysis on magnetostrictive properties of silicon steel sheet under harmonic magnetic field[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 545-550.

[22] 迟青光, 张艳丽, 陈吉超, 等. 非晶合金铁心损耗与磁致伸缩特性测量与模拟[J]. 电工技术学报, 2021, 36(18): 3876-3883.

Chi Qingguang, Zhang Yanli, Chen Jichao, et al. Measurement and modeling of lossand magneto- strictive properties for the amorphous alloy core[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3876-3883.

[23] 杜杲娴, 杨鑫, 韦艳飞, 等. 稀土超磁致伸缩棒材特性测试平台优化与实验研究[J]. 电工技术学报, 2021, 36(18): 3867-3875.

Du Gaoxian, Yang Xin, Wei Yanfei, et al. Optimi- zation and experimental research on the test platform of rare-earth gaint magnetostrictive rod characteri- stics[J]. Transactions of China Electrotechnical Society, 2021, 36(18): 3867-3875.

[24] 赵志刚, 马习纹, 姬俊安, 等. 谐波激励条件下铁心动态Energetic建模与验证[J]. 电工技术学报, 2020, 35(20): 4241-4250.

Zhao Zhigang, Ma Xiwen, Ji Junan, et al. Dynamic energetic modeling and verification of core under harmonic excitation[J]. Transactions of China Elec- trotechnical Society, 2020, 35(20): 4241-4250.

[25] 王园弟, 张艳丽, 张殿海, 等. 旋转磁化下电工钢片磁致伸缩动态矢量特性模型[J]. 中国电机工程学报, 2018, 38(1): 292-299, 367.

Wang Yuandi, Zhang Yanli, Zhang Dianhai, et al. Dynamic vector property model of magnetostriction in an electrical steel sheet under rotational mag- netization[J]. Proceedings of the CSEE, 2018, 38(1): 292-299, 367.

[26] 戴道生. 物质磁性基础[M]. 北京: 北京大学出版社, 2016.

[27] Baghel A P S, Kulkarni S V. Dynamic loss inclusion in the Jiles-Atherton (JA) hysteresis model using the original JA approach and the field separation approach[J]. IEEE Transactions on Magnetics, 2014, 50(2): 369-372.

[28] Hussain S, Lowther D A. The modified Jiles-Atherton model for the accurate prediction of iron losses[J]. IEEE Transactions on Magnetics, 2017, 53(6): 7300504.

[29] 张艳丽, 孙小光, 谢德馨, 等. 无取向硅钢片各向异性磁致伸缩特性模拟[J]. 中国电机工程学报, 2014, 34(27): 4731-4736.

Zhang Yanli, Sun Xiaoguang, Xie Dexin, et al. Modeling of anisotropic magnetostriction property of non-oriented silicon steel sheet[J]. Proceedings of the CSEE, 2014, 34(27): 4731-4736.

[30] Ito S, Mifune T, Matsuo T, et al. Energy-based mag- netization and magnetostriction modeling of grain- oriented silicon steel under vectorial excitations[J]. IEEE Transactions on Magnetics, 2016, 52(5): 2002604.

[31] 王振, 张艳丽, 任亚军, 等. 铁心表面局部磁特性检测系统设计与实现[J]. 电工技术学报, 2018, 33(23): 5435-5441.

Wang Zhen, Zhang Yanli, Ren Yajun, et al. Design and implementation of detection system of local magnetic property on the surface of iron core[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5435-5441.

Modeling of Magnetostrictive Characteristics in an Electrical Steel Sheet Based on the J-A Model and Its Experimental Verification

（School of Electrical Engineering Shenyang University of Technology Shenyang 110870 China）

The magnetostrictive phenomenon in the electrical steel is an important cause of vibration of the iron core in motors and transformers. Magnetostrictive characteristics are close related to magnetization patterns of iron cores. There is a large amount of rotating magnetic field in the stator core of electric machines, and compared with alternating magnetization, the rotating magnetization will cause greater magnetostrictive strain. Therefore, accurately modeling the magnetostrictive characteristics in an electrical steel sheet under rotating magnetization is the basis and premise for optimizing the performance of electrical equipment. In this paper, using the Jiles-Atherton (J-A) hysteresis model to characterize the hysteresis behavior caused by the movement of the magnetic domain wall and the rotation of the magnetic moment during the magnetization process, a magnetostrictive model that can describe the vector and hysteresis characteristics of magnetostrictive normal and shear strains under rotating magnetization is proposed. Based on the characteristic data in an electrical steel sheet provided by the rotating magnetic characteristic measurement system, the particle swarm optimization algorithm was used to identify model parameters, and the accuracy of the model was verified. A measurement system of local magnetostrictive properties in silicon laminated cores was set up, and the specific process of calculating the magnetostrictive deformation of the core was presented. By comparing with the measurement results, the validity of the model was further investigated. It is shown that the magnetostriction of electrical steel sheets under rotating magnetization has hysteresis behavior, and the proposed model can effectively predict this kind of characteristics.

Rotating magnetization, magnetostriction, electrical steel sheet, J-A model

10.19595/j.cnki.1000-6753.tces.211404

TM275

国家自然科学基金资助项目（52277015）。

2021-09-03

2021-10-08

李岱岩 男，1993年生，博士研究生，研究方向为电工材料复杂电磁特性的测量、模拟与应用。E-mail: 1052870137@qq.com

张艳丽 女，1975年生，教授，博士生导师，主要研究方向为电工装备多物理场与电工材料特性。E-mail: ylzhang@sut.edu.cn（通信作者）

（编辑 崔文静）