基于模糊贝叶斯-ANP舰载机出动回收综合评估

邓嘉宁, 吴 宇, 许舒婷, 苟进展

(1. 重庆大学航空航天学院, 重庆 400044; 2. 北京航空航天大学航空科学与工程学院, 北京 100191)

0 引 言

航空母舰作为二战中及战后新世界的国家级战略装备,其具备的军事功能、科技与经济功能、外交功能、警察功能等为国家经济、安全、主权提供了强大保障。其中,舰载机的出动回收能力是衡量航母战斗力的重要指标,优化舰载机的出动回收流程能够使得单位时间内舰载机的起降数量得到大幅提升。舰载机在航母上的出动回收流程主要分为以下过程:舰载机起飞前的保障,机库调运,甲板调运、滑行、起飞,起飞后甲板保障,降落前保障、着舰,回机库和任务执行后的保障等流程。由于涉及的人员、设备、工序等错综复杂,提炼影响舰载机出动回收能力的关键性指标将会对提高航母战斗能力起到重要指导作用。

在舰载机出动回收流程关键指标的确立方面已有相关研究。对于舰载机的调运作业,文献[5]对比了舰载机在甲板上调度的3种模式,即自主滑行、无牵引杆的牵引系统和带牵引杆的牵引系统,结合智能算法进行仿真,对不同模式的优劣进行了分析。对于舰载机甲板调运作业,文献[6-7]提出了分层协同规划结构,建立了协同路径规划数学模型,对于舰载机多机协同起飞降落的动态多目标优化问题进行了研究。关于飞行甲板统一调度方面,文献[8]提出了关于下一代飞行甲板自动化调控辅助设备的原型,该设备基于人的行为准则、认知、行动建模,能够评估和比较潜在的自动化调控方案,并确定潜在的人机交互问题。文献[9]将舰载机着舰回收过程中的调度问题抽象为满足尾流间隔、剩余燃油及跑道复位等约束的随机规划模型,提出了基于飞机优先顺序指标函数的蒙特卡罗模拟-差分进化搜索的实时调度算法,解决了由于飞机故障、着舰复飞逃逸等因素产生的动态随机调度问题。为保障舰载机的安全,文献[10]对舰载机着舰环境进行了研究，在描述甲板环境后,对航母运动进行建模,包括确定性模型和随机模型，分析了大气扰动的变化规律,进而设计了水平尾流、横向尾流和垂直尾流3个组件,集成了舰载机着舰系统。

上述论文对于舰载机出动回收的单个或者多个流程进行了研究,但缺乏对于整个出动回收流程的关注。文献[11]通过对美国、英国、法国和俄罗斯几个典型案例的分析,对舰载机出动回收能力的基本概念：出动架次率、飞行日长度、特定任务等进行了研究,提出了衡量出动回收能力指标的主要特征,并从设备、工作人员和环境3个方面出发,分析了影响舰载机出动回收能力的主要因素。同时，文献[12]通过分析各因素之间的耦合影响度,建立了舰载机航空保障网格化指标体系。其中,指标体系以控制指挥、起飞保障、转运保障、拦阻着舰、舰面保障和维修支援6个方面为主,建立了相对完善的舰载机航空保障效能评估体系。此外，文献[13]以美军航母公开数据为基础,对其航母舰载机出动回收能力和飞行甲板控制策略进行了研究,采用调度模型台推演舰载机出动和回收过程,并对航空保障的限制因素进行分析,归纳出保证美军航母出动架次率的重要因素,进而总结出美军航母飞行甲板控制策略。

随着航母国产化进程的加快,上述关于舰载机出动回收的某个或多个环节的研究不能满足海军发展的需求,因而对于航母舰载机出动回收全过程中关键指标的研究将会对海军整体战斗能力的提升起到重要指导和参考作用。本文将基于以上文献的研究,结合实际情况从人、机、环3个方面出发,以文献[12]中舰载机保障评价体系为基础,扩展建立了由顶层指标、子系统层指标和设备层指标组成的描述舰载机出动回收能力的3层指标体系,以便更加详细具体地研究影响舰载机出动回收能力的关键性指标。同时，关于舰载机出动回收能力指标体系的分析方法,普遍使用较多的是面向内部独立递阶结构的层次分析法(analytic hierarchy process, AHP)和面向内部依存复杂结构的网络层次分析法(analytic network process, ANP),而由于航母舰载机出动回收流程的复杂性,即在子系统层内的设备层指标之间并非完全独立,AHP无法准确反映设备层指标的复杂联系,因此ANP比AHP更加适合。

本文将首先建立航母舰载机出动回收能力评价体系;然后结合三角模糊数和扩展贝叶斯融合法确定指标之间的相互关系,在此基础上建立用于计算分析的ANP模型;其次通过得到的ANP模型,基于提出的三角模糊数评价尺度标准和模糊数标准化方法,结合历史实验数据进行综合评价;最后进行了多组结果对比分析,验证了所提方法的有效性。

1 舰载机出动回收评价体系的建立与指标相互关系的确定

在本节研究中,首先建立能够系统、全面体现舰载机出动回收能力的评价体系;再根据建立好的评价体系设计问卷,专家将根据问卷,基于信心度和关系度,对指标之间的相互关系进行评判,最终评判的结果将决定评价体系中设备层指标的相互关系。

1.1 舰载机出动回收能力评价体系建立

建立舰载机出动回收效能评价体系,将涉及对舰载机保障的各个系统、各个流程进行系统完备的分析。本文重点关注关键性的评价指标,建立有序、有效的网络结构层次评价关系,进而提出能综合全面体现舰载机保障能力的有效评价体系,形成航母舰载机保障能力决策层向因素层的有效映射。

根据实际作战需求,以舰载机出动回收能力作为顶层指标;将舰载航空保障系统分为舰载机搭载能力、舰载机起飞保障能力、拦阻着舰保障能力、航空指挥控制能力、舰面保障能力、维修支援保障能力和人员保障能力7个部分的子系统层;位于最底层的为设备层指标,整个舰载机保障评价指标系统的组成如图1所示。

图1 舰载机出动回收能力评价系统Fig.1 Carrier aircraft’s dispatch and recovery capability evaluation system

1.2 基于三角模糊数的扩展贝叶斯融合法指标关系的确定

在利用ANP对舰载机出动回收能力评价体系进行综合评估之前,需要对体系内的设备层指标之间的相互关系进行确定,即区分设备层指标之间的因果关系,进而确定设备层指标从属的子系统层之间的相互关系。

1.2.1 扩展的贝叶斯融合法

在建立了完备的舰载机出动回收能力评价体系之后,需要专家对各底层指标之间的相互关系进行评判打分。基于专家评判打分的结果,采用以贝叶斯决策理论为基础的扩展贝叶斯融合法进行处理，其中，为描述两个指标之间的相互关系,引入信心度和关系度(表示为[,])进行综合评判,其中信心度和关系度均在0到1之间,即:0≤≤1,0≤≤1,根据扩展的贝叶斯融合法有:

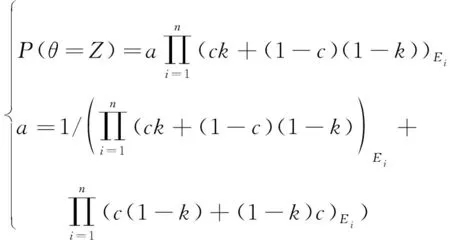
(1)

式中:是标准化因子;(=)表示在评判准则下,评价体系中指标与指标之间存在相互关系的概率;表示参与评判的第位专家。

根据式(1)得到的指标间存在的相互关系进行融合分析,建立指标之间相互影响度的判断矩阵=,,∈(1,),∈[0,1],表示在指标变化下指标对应受影响的程度。对于ANP所需要的网络化指标评价体系而言,只需要确定指标之间存在关系与否,在本体系中,将指标之间是否存在关系的概率阈值定为05,即:当0≤<05时,=0;当05≤≤1时,=1。当概率为0时表示两个指标与不存在相互关系,当概率为1时表示两个指标与存在相互关系,由此得到指标之间是否存在关系的0-1判断矩阵。

122 三角模糊数评判标准的建立与标准化方法

由于在舰载机出动回收能力评价体系中,各个指标间的相互关系比较复杂,对于复杂关系的评判无法用准确单一的数字进行具体描述。因此,引入模糊判断语言变量与三角模糊数变化量,对专家在评判时信心度和关系度的具体范围进行规定,如表1所示。

表1 模糊判断语言变量及数值表示Table 1 Fuzzy judgment language variables and numerical representation

表1所示的三角模糊数表明了专家在对指标影响关系及自身判断信心度的大致判断范围,为便于后续计算和计算结果的有效性,需要对判断矩阵里的三角模糊数进行去模糊标准化处理,去模糊化过程如下。

记三角模糊数的范围:(,,),位专家的评判分别记为:(,),(,),…,(,)。

(1) 专家判断语言数值信息的三角模糊数标准化

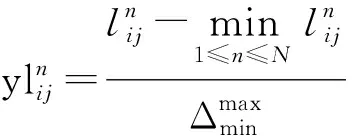
(2)

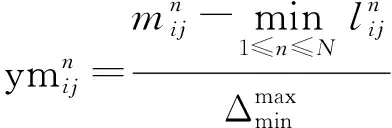
(3)

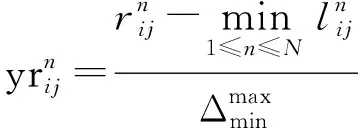
(4)

(2) 计算三角模糊数标准化数值的左右限值

(5)

(6)

式中：yls、yrs分别表示专家的信心度或关系度模糊数标准化过程中的最大最小限值。

(3) 计算三角模糊数标准化数值的总值

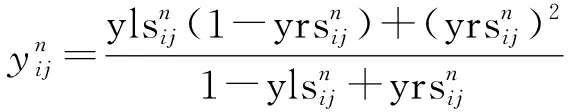
(7)

(4) 计算专家对于指标与指标的信心度或关系度的精确值

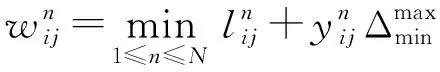
(8)

由于其中信心度和关系度均表示专家对于指标相互关系的判断,且数据结构相同,故均可由式(2)～式(8)处理。可表示各个专家模糊评判值(,)经过去模糊化得出的单一标准化数值(,)。

(5) 根据标准化后的信心度进行归一化处理

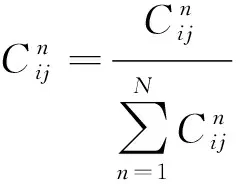
(9)

(6) 利用标准化后的关系度和归一化处理的信心度根据式(1),确定指标与指标存在相互关系的概率矩阵

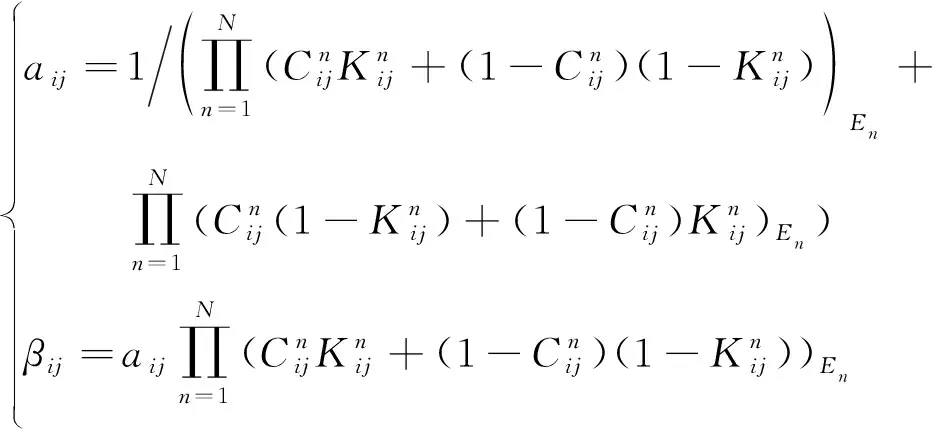
(10)

123 建立ANP分析模型

为了建立用于ANP分析的模型,首先需要由多位专家,根据表1的三角模糊数,对所有设备层指标之间的信心度和关系度进行评判;然后再按照式(2)～式(9)进行标准化处理得到标准化数值(,);最后再利用贝叶斯融合法,确定设备层指标之间的相互关系概率矩阵,同时对根据概率阈值进行0-1化处理。

根据得到的指标之间是否存在关系的0-1判断矩阵,建立的ANP模型如图2所示。

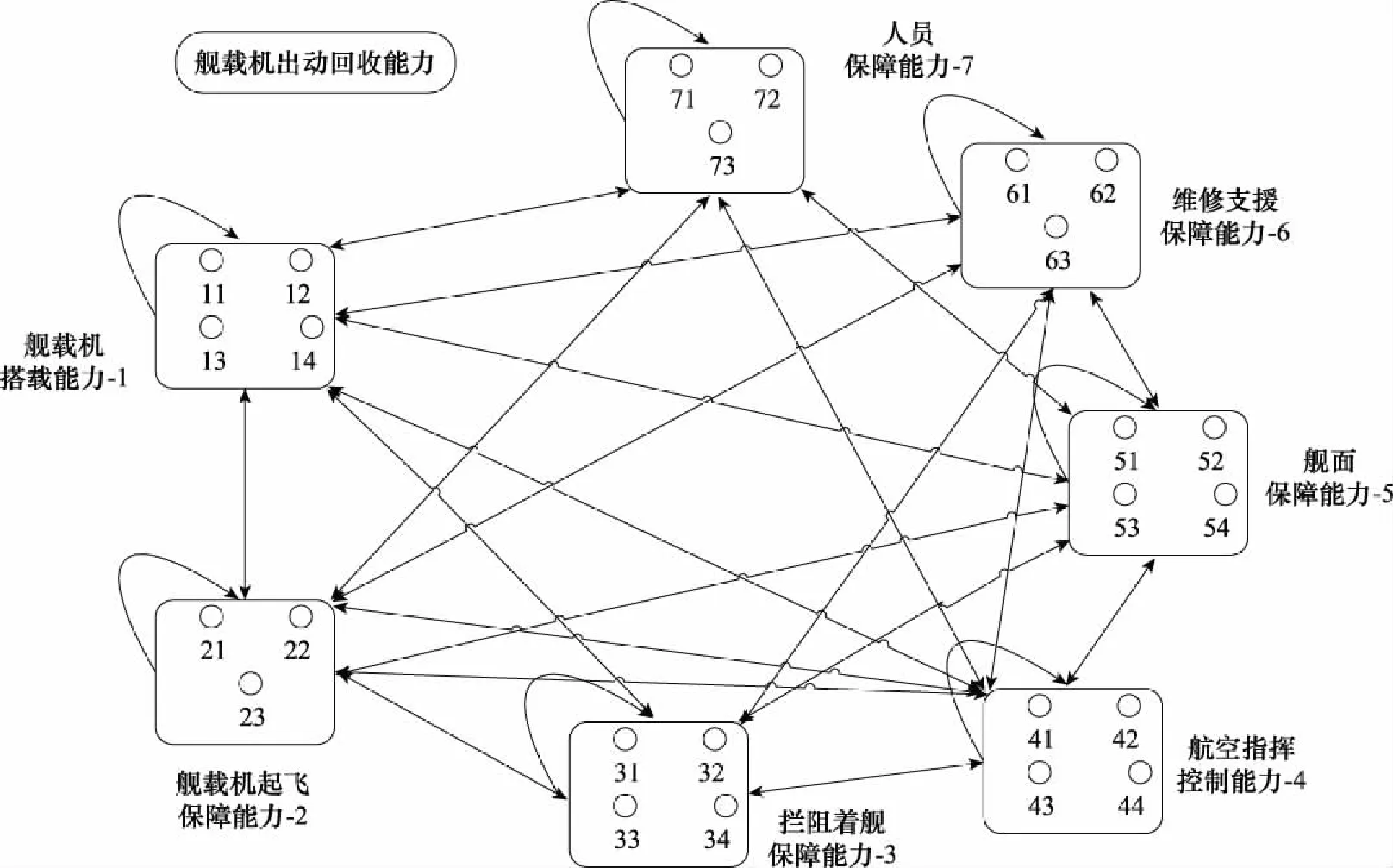
图2 舰载机出动回收能力评价模型示意图Fig.2 Schematic diagram of carrier aircraft’s dispatch and recovery capability evaluation model

在ANP的网络模型中,子系统层之间的关系由设备层指标决定,如:11→14、21、22、23、41、42、43、44、51、53、54、61、63、71、72,表示指标11的变化会引起箭头后其他指标的变化。同时，包含上述设备层指标的子系统层之间也存在关系:1→1、2、4、5、6、7,表示舰载机搭载能力-1的变化会引起保障能力-2、航空指挥能力-4、舰面保障能力-5、维修支援能力-6、人员保障能力-7的变化,其中指向自己的箭头表示同一子系统层内的设备层指标存在相互关系。

2 基于模糊数的多源数据综合权重确定

在利用ANP进行设备层指标在整个系统中权重占比计算之前,需要根据第12节确定的设备层指标之间的相互关系,基于相关准则尺度标准进行综合评判,常用的评判准则是经典1～9尺度标准,本文为了贴合人为评判的模糊性和不确定性,采用了一种基于三角模糊数的尺度标准,经去模糊化后,结合历史实验数据和专家评判确定最终综合权重。

2.1 基于三角模糊数的评判标准与去模糊化

在经典ANP中,设备层指标之间和分系统层指标之间的重要性评判普遍采用1～9标度法,为了保证专家的评判更加符合客观规律,本文采用了如表2所示的基于三角模糊数的评价法。

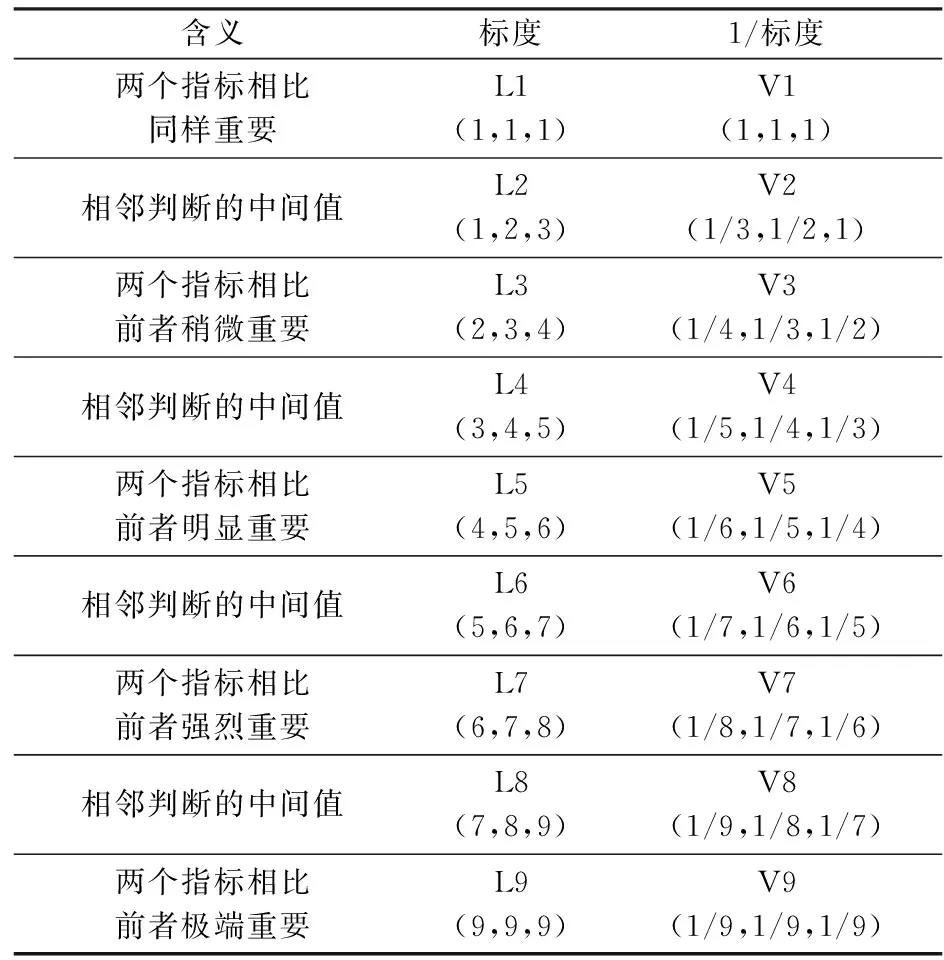
表2 基于三角模糊数的ANP评判标度Table 2 ANP evaluation scale based on triangular fuzzy number

在以1～9标度法的ANP判断矩阵中,对角线元素始终为1,并且关于对角线对称的元素相乘为1,为了保证基于模糊数的判断矩阵也具有上述特征,在新的判断矩阵中,对角线元素定为(1,1,1)。按照如表2所示的三角模糊数标度的判断矩阵,给出一个示例,如表3所示。

表3 三角模糊数标度判断矩阵Table 3 Judgement matrix of triangular fuzzy number scale

在表3中,第2行第3列中的(4,5,6)表示相比于指标2,指标3明显重要。

对于ANP判断矩阵中三角模糊数的去模糊化,需要综合考虑多个专家的判断矩阵时,每个专家的判断矩阵均采用式(2)～式(8)。虽然在进行指标之间重要性评判时未采用第1.2.1节中基于信心度与掌握度的融合贝叶斯法,但对不同专家意见采取了不同的考虑权重,同时配合文献[33-34]所提式(2)～式(8)采用的模糊数尺度标准,也能避免专家极端分歧产生结果失真的情况。同时，需要对去模糊后生成的判断矩阵进行一致性检验,如果判断矩阵的平均随机一致性比例大于等于0.1,则认为该矩阵的一致性是不能接受的,需要组织专家重新进行判断以满足一致性要求。

2.2 通过历史实验数据确定判断矩阵

通过收集航母舰载机系统出动回收过程中的相关数据,计算得到不同指标的历史实验数据,用于确定两个指标之间的相对重要度判断矩阵,设个影响指标的历史实验数据为=[,,…,],个被影响指标的历史实验数据为=[,,…,],其中对于指标之间的相互关系可采用最小二乘法进行确定,即两个指标的历史数据经过一维线性拟合得到关系模型=+,进而可以求得和,两个指标对应的比例关系为,令=[,,…,]，通过拟合得到的,对两个需要判断的指标进行一维线性关系斜率比较,得到历史实验数据的判断矩阵为

(11)

式中:对、取绝对值是为了消除指标之间负相关对于判断矩阵中出现负数的影响。在ANP中,任意两个设备层指标或者子系统层指标重要性对比的数值不能为负,若由历史实验数据线性拟合得到的斜率和不取绝对值,当其中一个为负数时,由式(11)得到的<0,不满足判断矩阵元素大于零的条件,无法进行接下来的权重占比计算,进而无法完成未加权超矩阵的建立。同时,若判断矩阵中存在负元素,计算得到的权重占比的数值存在负数,不符合实际。

由式(11)产生的判断矩阵不符合1～9标度判断标准,可能会造成ANP的极限超矩阵不收敛,因此将判断矩阵进行标准化处理:

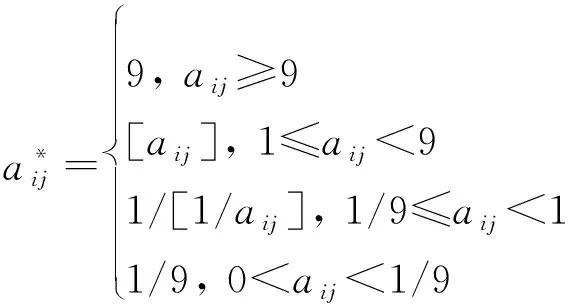
(12)

2.3 专家评估与历史实验数据融合

通常在对设备层指标之间或者子系统层指标之间根据ANP判断尺度标准进行评判时,有两种途径:一是通过收集专家基于经验略带主观性的判断矩阵,二是通过对采集的历史实验数据对某些指标进行定量分析后,确定指标之间的关联度,从而构建基于历史实验数据的判断矩阵。为了使得到的指标判断矩阵更加准确,将具有主观性的基于专家经验的判断矩阵和客观性更强的历史实验数据得到的判断矩阵进行融合处理,同时根据不同判断矩阵的来源、重要性、权威性,设置不同的参考权重。

以融合两个判断矩阵为例,设=()×,=()×为两个不同的判断矩阵,和为和分别所占的比重且+=1,定义判断矩阵、融合后的判断矩阵为:

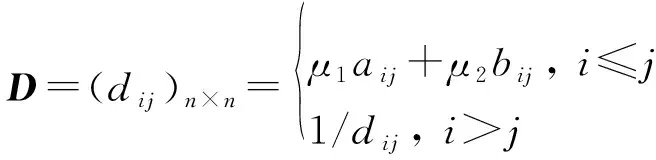
(13)

对于融合专家评估和历史实验数据所得到的判断矩阵进行一致性比例判断,若符合一致性要求,将判断矩阵进行和法权重计算:

(14)

2.4 ANP权重计算

241 子系统层指标之间权重超矩阵

由式(14) 可以得到关于多评价源的综合判断矩阵权重列向量,将其作为子系统层指标之间权重超矩阵子列向量,得到权重超矩阵;指标集间权重超矩阵表示了指标集之间的权重占比(列和为1),指标集间权重超矩阵将为指标间未加权超矩阵提供加权处理。

为了之后与指标之间的超矩阵所对应,将扩展为如表4所示形式。

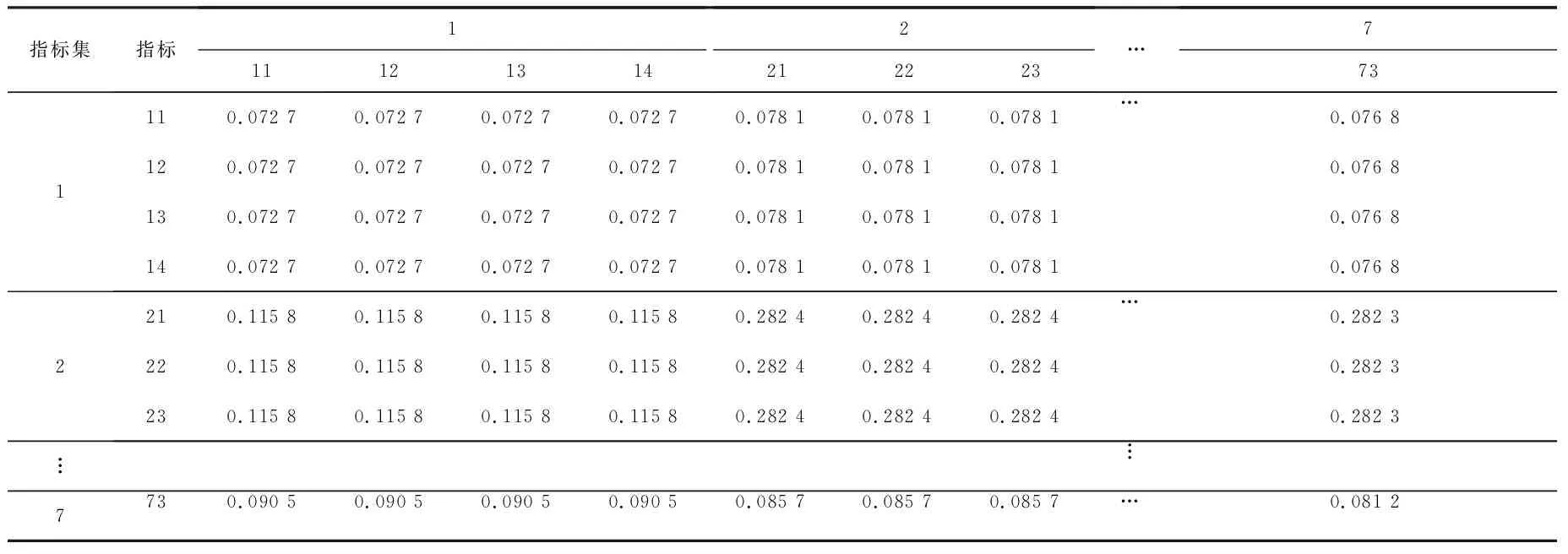
表4 扩展后的子系统层指标之间权重超矩阵Z25×25Table 4 Extended weight super matrix Z25×25 between the indicators of subsystem layer

2.4.2 设备层指标之间加权超矩阵

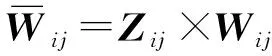
(15)

式中：是第241节中表4所示扩展后的子系统层指标之间权重超矩阵。

243 极限超矩阵与权重

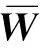
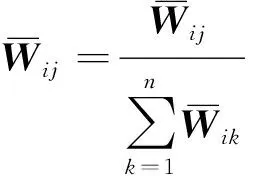
(16)

3 仿真算例研究

本文采用模糊ANP方法与经典ANP方法进行对比,从采用的尺度标准及融合历史实验数据与否两个方面进行算例仿真对比分析,模糊ANP方法与经典的ANP方法的主要特点如表5所示。(对于本文所涉及的程序计算,采用spyder进行计算:python版本3.8.0)。

表5 经典ANP与模糊ANP比较Table 5 Comparison between classical ANP and fuzzy ANP

3.1 融合专家评价和历史实验数据方法的验证

为了验证专家评价结果和历史实验数据所得到数据的一致性,将融合专家评价与数据同仅考虑专家评价的最终权重占比排序进行对比分析,得到的权重具体占比如表6所示。其中，权重1和排序1是综合了专家和数据得到的结果,权重2和排序2是只有专家评价的最终结果。

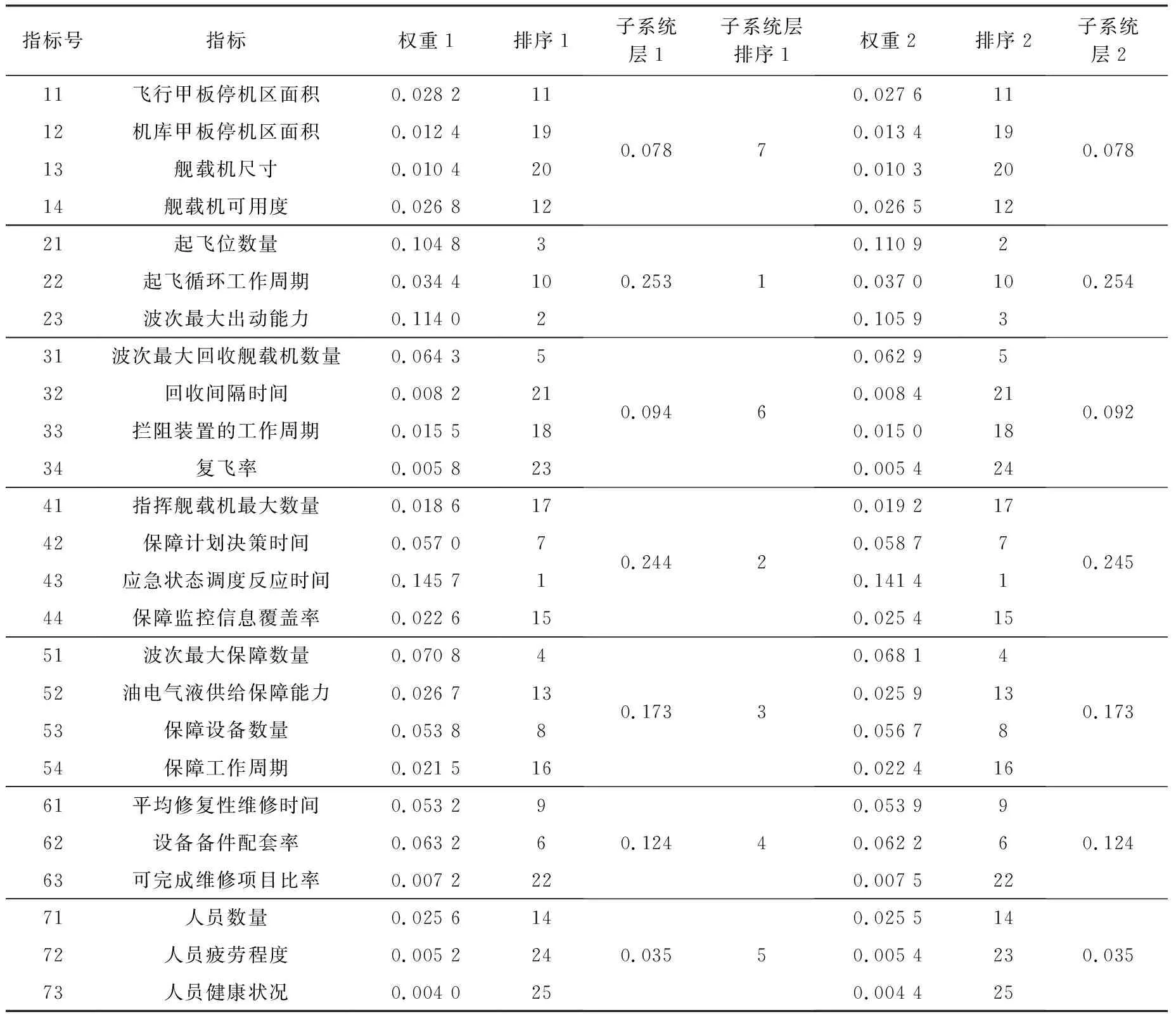
表6 舰载机出动回收能力评价体系指标权重排序(融合历史实验数据与否)Table 6 Indicator weight ranking of carrier aircraft’s dispatch and recovery capability evaluation system (Combined with historical experimental data or not)

对表6中的数据进行分析,可得到如下结论:

(1) 排序靠前的关键性指标有起飞位数量和波次最大出动能力,排序靠后的非关键性指标有人员疲劳程度和复飞率,以上4个底层指标在整个舰载机出动回收能力权重占比排序中存在差异,而其他指标的权重占比无差异;并且两种方法关于子系统层的权重排序无差异,说明综合专家评判与融合专家和数据的评判大致相符。

(2) 关键性指标起飞位数量和波次最大出动能力存在差异,说明在未融合数据仅靠专家主观评判存在一定程度的结果失真,为了更好地体现结果的客观真实性,需要综合考虑专家意见和历史实验数据。

(3) 在舰载机出动回收能力评价体系指标权重排序中,排在前五的分别是:应急状态调度反应时间、波次最大出动能力、起飞位数量、波次最大保障数量、波次最大回收舰载机数量。以上5个指标分别涉及了航空指挥控制能力、舰载机起飞保障能力、舰面保障能力、拦阻着舰保障能力4个方面。并且由文献[11]可知，在战时紧急状态下,应急状态下调度反应时间至关重要,同时起飞位数量，最大的出动、保障、回收能力也对于舰载机的出动回收能力影响极大,关注并改善这些因素对于提升舰载机出动回收能力将有显著效果。

3.2 模糊ANP与经典ANP对比分析

为了验证模糊ANP相对于经典1～9尺度标准ANP的合理性,采用模糊标度进行评判的底层指标最终权重排序和采用1～9尺度标准评判的结果进行对比分析,得到的权重具体占比如表7所示。其中，权重3和排序3是采用模糊标度得到的结果,权重4和排序4是采用1～9尺寸标度得到的最终结果。

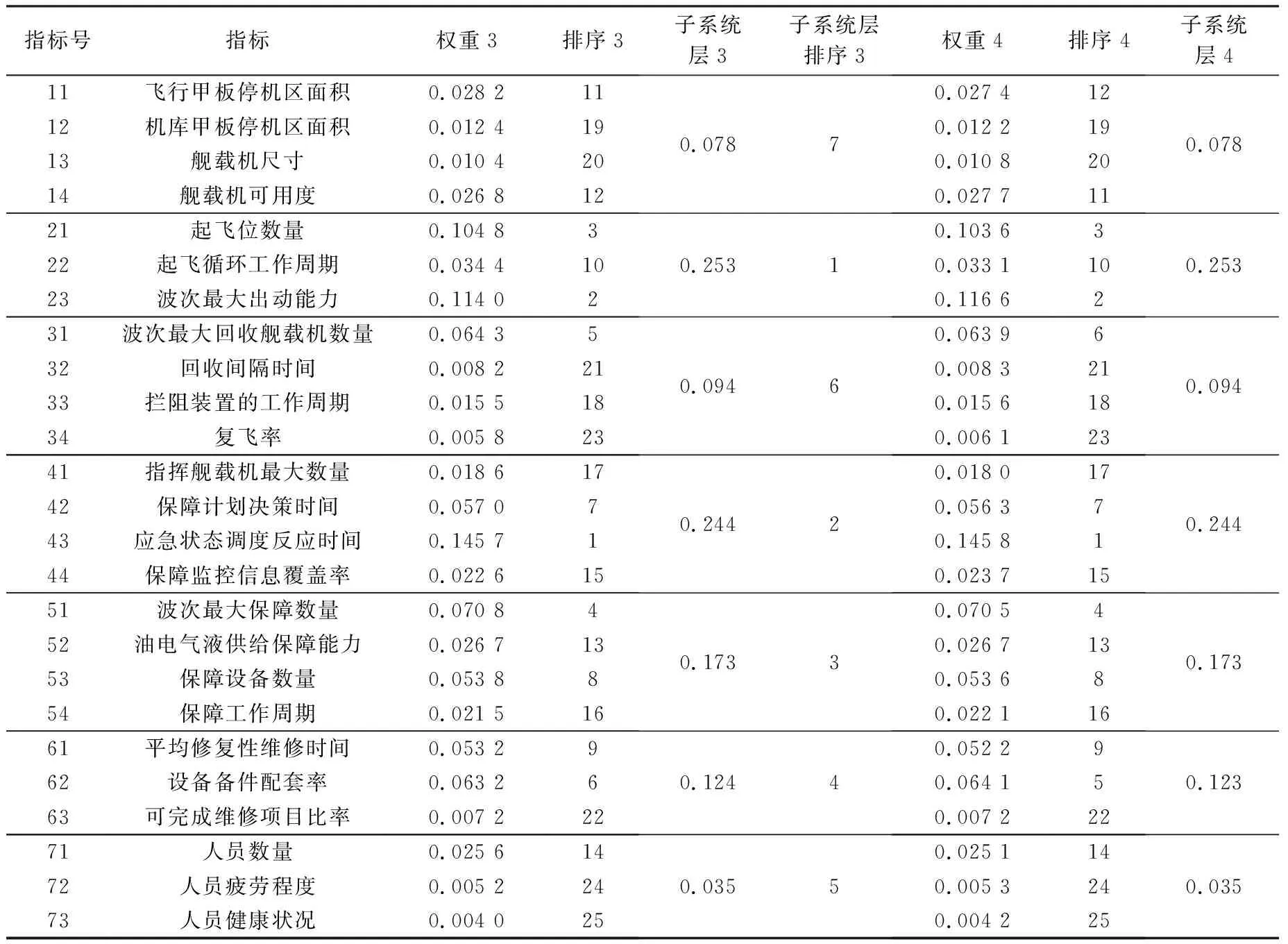
表7 舰载机出动回收能力评价体系指标权重排序(模糊ANP与经典ANP)Table 7 Indicator weight ranking of carrier aircraft’s dispatch and recovery capability evaluation system (fuzzy ANP and classical ANP)

在表7中,设备备件配套率、波次最大回收舰载机数量,以及舰载机可用度和飞行甲板停机区面积,上述4个设备层指标的排序存在差异,其他的指标排序无变化。同时，子系统层权重排序也无差异,说明基于三角模糊数的ANP具有和经典ANP具有一致的合理性。

4 结束语

科学评价舰载机出动回收效率对于提升航母舰载机系统战斗力具有重要意义。本文首先根据文献和实际情况建立了综合考虑人员、设备、环境的舰载机出动回收能力评价体系;然后根据建立的评价体系设计问卷,基于三角模糊数,由综合专家信心度和掌握度的扩展融合贝叶斯法确定设备层指标之间的相互联系;最后通过基于三角模糊数的尺度标准,对子系统层指标之间、设备层指标之间进行重要性评判,经由计算出设备层指标权重占比,完成算例的仿真研究。在确定指标相互关系时,对于提出的基于三角模糊数的扩展贝叶斯融合法,在信心度和关系度对于判断的相互约束与相互补充下,比经典ANP中单个数值进行评判更加符合人为主观判断的模糊性和不确定性。同时，基于三角模糊数的ANP评价尺度标准,相比于经典ANP准确数字1～9尺度标准,判断更具客观性。改进的模糊ANP与经典ANP分析得到的权重无明显差异,也表明了本文所采用方法的相对正确性。此外，在评判中加入历史实验数据,与专家评判相融合后,使得评判结果比只靠专家评判的经典ANP更具客观性。综上，本文采用的模糊ANP更加适合舰载机出动回收效率的评估。