联合准则下的认知雷达波形设计

曹亚丽, 李梅梅, 屈诗涵, 宋 昕

(1. 东北大学秦皇岛分校计算机与通信工程学院, 河北 秦皇岛 066004;2. 西安交通大学信息与通信工程学院, 陕西 西安 710049)

0 引 言

认知雷达从目标回波中获得环境信息,充分利用目标与环境知识改善发射信号的能量分配,不断优化发射波形,实现其自适应性。目前,波形优化主要以提高雷达目标参数估计性能、检测性能、信号分辨率、杂波抑制能力和抗电子干扰能力为目的。设计波形时常用的优化准则有最大化互信息、最大化信干噪比、最小均方误差(minimum mean squared error, MMSE)、最小化模板匹配误差准则等。

信息论在波形设计方面有着广泛的应用,文献[2]首先提出最大化雷达目标和回波之间的互信息来设计发射波形的方法,接收信号与目标冲激响应之间的互信息越大,目标识别或目标参数估计性能越好,以最大化互信息为优化准则,通过拉格朗日乘子法求解最优波形。文献[3]提出一种基于双互信息优化准则的自适应波形设计方法。该方法同时以接收信号与目标冲激响应之间的互信息最大和接收信号与杂波冲激响应之间的互信息最小为优化准则,在发射信号能量有限的约束条件下,建立优化模型,通过最大边缘分配算法求解最优波形。文献[4]推导了互信息的边界和信干噪比的作用阈,并在信号相关杂波环境下,提出一种信干噪比约束下基于最大化互信息的波形设计方法,证明了在有目标且杂波弱的频率点可优化波形并提取目标信号。文献[5]通过设计接收滤波器和发射波形来最大化信干噪比,最大程度地提高雷达的探测能力。文献[6]提出了一种博弈条件下的雷达波形设计方法,采用 Stackelberg 博弈框架进行建模,以优化雷达能量谱分布为策略,采用最大互信息准则建立效用函数，经过多次迭代,双方达到纳什均衡,实现了雷达发射波形的优化。文献[7]以雷达发射功率作为约束条件,以最大化目标与接收回波间的互信息为目标,对认知多输入多输出雷达的波形设计问题进行建模,并采用卡尔曼滤波一步预测的方法对快速运动扩展目标的冲激响应进行预测,实现对目标的精准估计。文献[8]提出了一种基于信噪杂比最大能量分配方法，该方法通过离散化的能量进行合理分配,获取回波的最大信干噪比,从而得到认知雷达的最优发射波形。文献[9]针对不同干扰环境、目标模型、天线配置等波形设计关键要素及主要思路进行了总结梳理，从不同干扰与目标知识的利用角度出发,充分利用目标与环境先验信息,设计雷达波形以提高目标检测、跟踪以及抗干扰等性能,从而实现自适应探测和处理。

本文在上述研究基础上,提出了将互信息与信干噪比联合作为优化准则,使用最大边缘分配算法,求解最优波形。依据参数的变化,联合准则下的雷达信号模型既可同时提高互信息和信干噪比值,又可根据发射需求分别优化互信息或信干噪比值,实现雷达信号模型的多模式和多任务化,为雷达波形优化朝着多功能模型设计提供参考和依据。

1 系统模型的建立

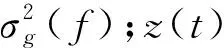
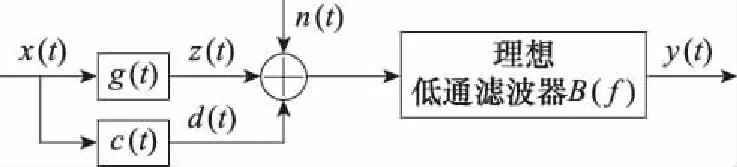
图1 独立杂波背景下的信号模型Fig.1 Signal model in the independent clutter background

()=()·()+()·()+()=()+()+()

(1)

其傅里叶变换为

()=()+()+()

(2)

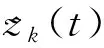
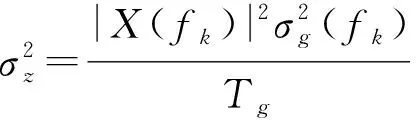
(3)

杂波信号的方差为

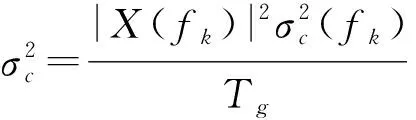
(4)

噪声信号的方差为

(5)

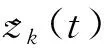
(6)

令互信息谱密度为

(7)

在整个信号频带内,随着区间带宽Δ→0,这些频率区间的数目不断增加,经过理想低通滤波器后,在极限思想下,得到目标和回波的互信息的积分表达式为

MI=(();()|())=()-(|)=

(8)

信干噪比是反映雷达检测性能的一个重要参数,在图1信号模型下,对于目标冲激响应(),可以得到信干噪比谱密度为

(9)

由于信号在一定时间内是平稳的,则在信号带宽内,定义在杂波背景下针对观测时间的目标接收端信干噪比为

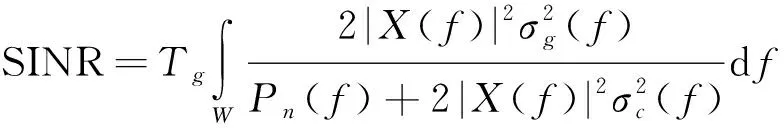
(10)

2 联合互信息与信干噪比准则

2.1 波形优化准则的建立

最大化互信息是衡量雷达目标识别和目标参数估计性能的优化准则,称为MI准则，最大化信干噪比是增强雷达目标检测性能的优化准则，称为SINR准则。由于认知雷达系统需要更加灵活的设计模型,该模型不仅针对单一任务的雷达波形设计,还能够满足多种雷达任务的发射波形设计。将互信息和信干噪比两个参数作为设计雷达波形优化准则的依据,同时定义参数、分别为联合准则中互信息和信干噪比的权重系数。在实际系统中,根据各种环境信息和发射需求,改变、值,可以使雷达发射波形的优化准则根据雷达发射需求不断调整,从而实现雷达的目标检测性能或目标参数估计性能的优化。联合互信息与信干噪比(mutual information and signal to interference noise ratio, MS)准则为

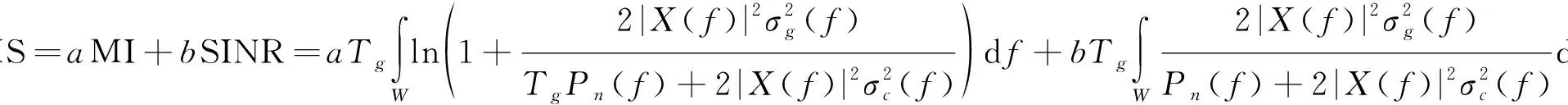
(11)

式(11)为雷达波形优化问题的目标函数,能量约束条件为

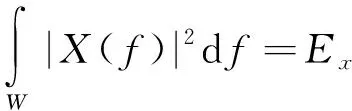
(12)

由于互信息与信干噪比谱密度存在指数关系,当最大化MS时,互信息和信干噪比值可同时最大化,也可分别最大化。互信息值越大,雷达目标参数估计越精确,因而最大化互信息通常作为目标参数估计和识别性能的准则。信干噪比值越大,雷达目标检测概率越高,所以信干噪比通常作为雷达检测性能的准则。MS可根据工作环境和发射需求,通过较少次观测数据实现雷达目标参数估计或目标检测性能的增强。

2.2 最大边缘分配算法求解优化波形

当杂波不存在时,信号模型可以通过拉格朗日乘数法求解,若存在杂波信号,在求解最优波形时,需要对乘子进行搜索,计算量大且繁琐。因此,采用最大边缘分配算法,通过能量的合理分配求解雷达最优波形。在最大边缘分配算法下,可以在相同的小频段Δ内对互信息和信干噪比的谱密度之和进行求值,将式(11)离散化为

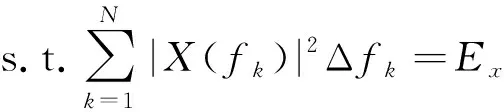
(13)

令：

()=|()|

(14)

(15)

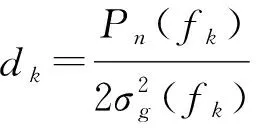
(16)

因此,可得

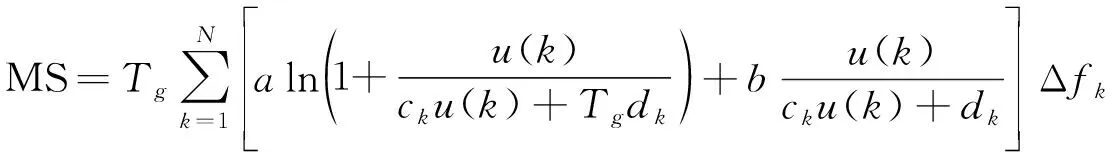
(17)

对MS约束下的雷达波形设计的优化问题,就转化为在能量约束下,最大化。其中：

(18)

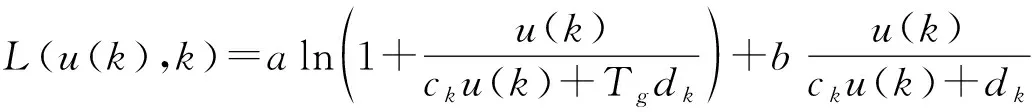
(19)

3 仿真结果和数值分析

3.1 仿真性能分析

为了分析最优波形的互信息和信干噪比的变化率以及联合优化准则中不同、值对雷达性能的影响,首先讨论当==1时,雷达波形的性能,其模型参数如下:假设杂波的功率谱密度和目标能量谱方差是已知的,信号的总能量为1,采样点数为512,目标长度和发射信号长度均设置为31,采样频率为2,信号的频率为∈[0,1],噪声功率谱密度为01,雷达波形如图2所示。

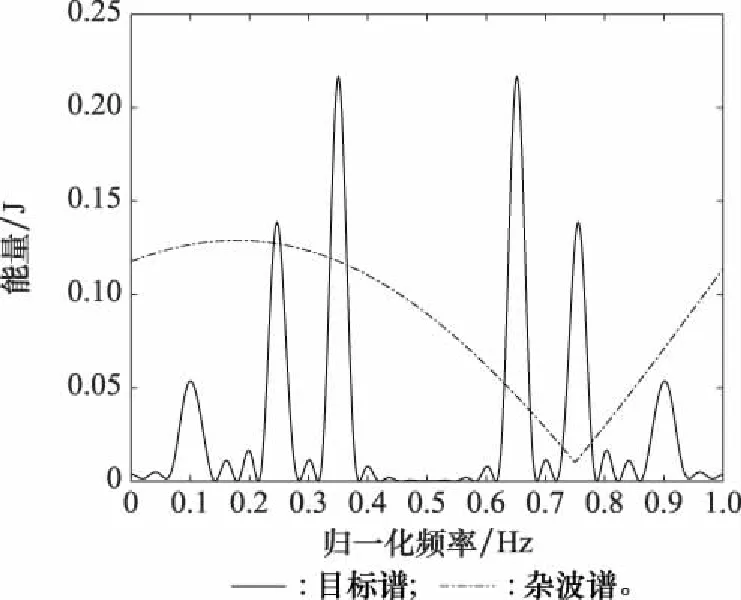
图2 目标谱和杂波谱Fig.2 Target spectrum and clutter spectrum

根据式(11)得到信号优化波形的能量谱如图3所示,从图3中的最优发射波形图可以看出,在某些杂波较小或为零的频带中,优化后的波形为该频带分配更多的能量,而在杂波影响较强的频带中,即目标波形相对虚弱的地方,将分配较少的能量,但仍得到了目标频谱。

图3 基于MS的优化波形能量谱Fig.3 Optimal waveform energy spectrum based on MS

表1为3种优化准则下,雷达波形设计的仿真数据,从表中可以看出,MS下的互信息值和信干噪比值优于单独任一准则下的数据,并且随着值的增加,Δ越小,最优波形不断精确,从而接近于一条光滑的曲线。但随着的增加计算量不断加大,本文综合考虑，值取为1 000,此时得到的最优波形较平滑且计算量适中。(基于MS的优化波形的互信息处于最大化互信息的优化波形的互信息和最大化信干噪比的优化波形的互信息数值之间,基于MS的优化波形的信干噪比处于最大化互信息的优化波形的信干噪比和最大化信干噪比的优化波形的信干噪比数值之间)。因此，MS则可以根据实际环境和发射需求,改变、值,实现雷达波形的不同性能需要。

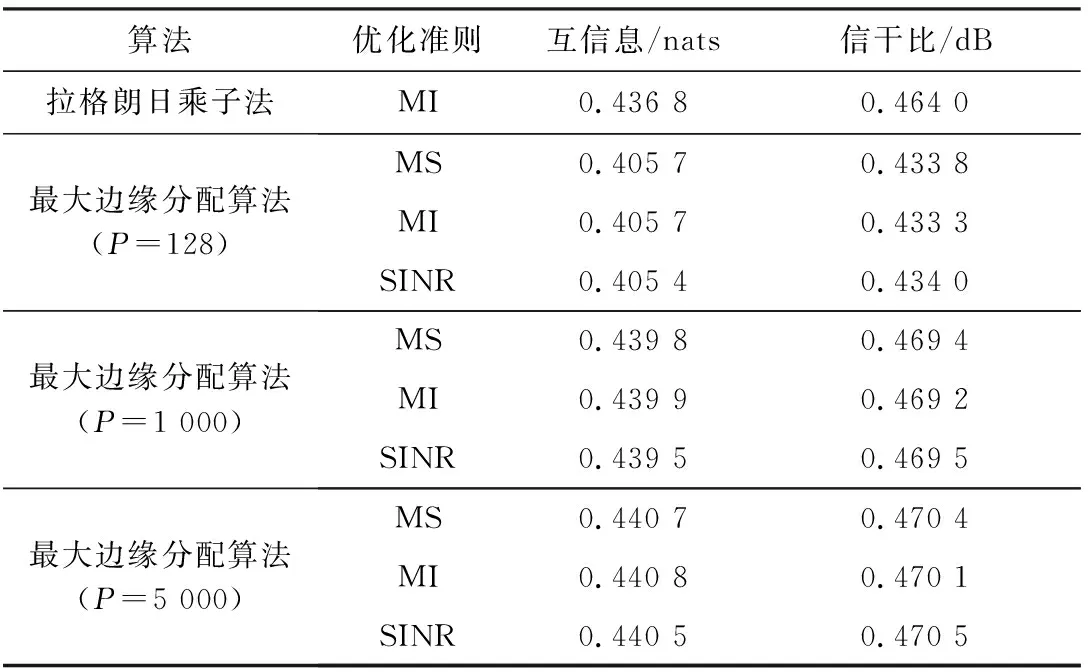
表1 不同优化准则下的互信息和信干噪比Table 1 Mutual information and SINR under different optimization criteria

3.2 关于系数的讨论

在=情况下分析了MS优化下雷达波形的性能后,下面讨论、取不同的值时,MS对雷达目标参数估计性能或检测识别性能的影响。当≠时,假设=1,=1,=,=,则MS()=MI+SINR,同时定义=mean(MI-SINR),mean指对括号内的一维矩阵求均值。图4为互信息和信干噪比关系的比较图,讨论了不同、值下,雷达波形最优时()=mean(MI-SINR)的解。

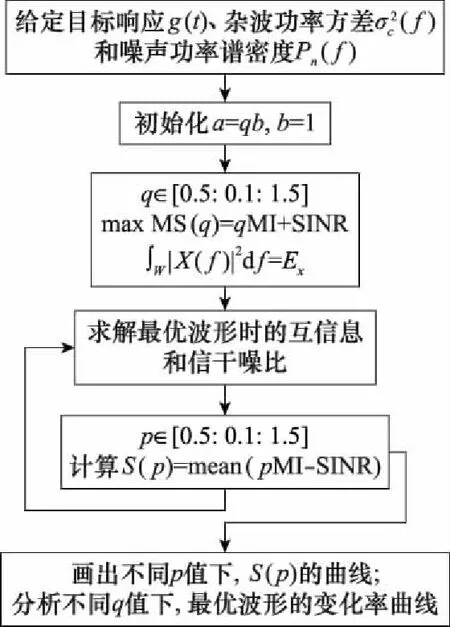
图4 互信息和信干噪比关系图Fig.4 Chart of the relationship between mutual information and SINR

当∈[05,15],取值间隔为01,可以得出()和的曲线如图5所示。拟合后发现()与轴的交点是(1058,0),因此,当=1058时,互信息和信干噪比在性能分析中的权重相同。当<1058时,相对于互信息而言,信干噪比权重大,此时雷达波形设计更偏向于优化信干噪比,雷达的检测性能会更好;当>1058时,互信息值权重大,说明对雷达波形的目标参数估计更精确,优化模型识别性能更好。

图5 S(p)和p关系曲线 Fig.5 Relationship curve of S(p) and p

为了进一步验证联合准则的性能,记录下最大边缘分配算法的每一步选择最大值的位置,画出不同值下能量分配到不同位置的变化率曲线,如图6所示。与=1点相比,最大边缘分配算法下的每一步选择最大值的位置变化率较大,因此可根据发射环境、发射需求、杂波特点等实际情况分配信号能量位置,实现波形优化。

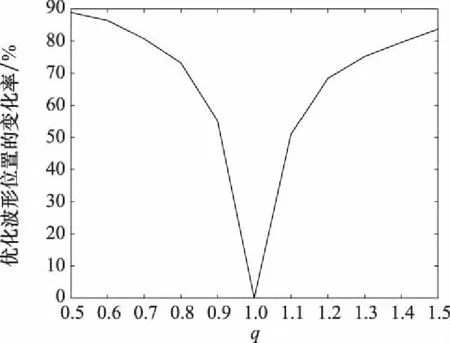
图6 不同q值下能量分配的位置变化率Fig.6 Position change ratio of energy distribution under different q

同理,使用最大边缘分配算法得到不同值下最优波形()的变化率,与=情况下的优化波形相比,波形变化的比率非常小。说明改变,雷达优化波形能量谱的趋势基本无变化,如图7所示。

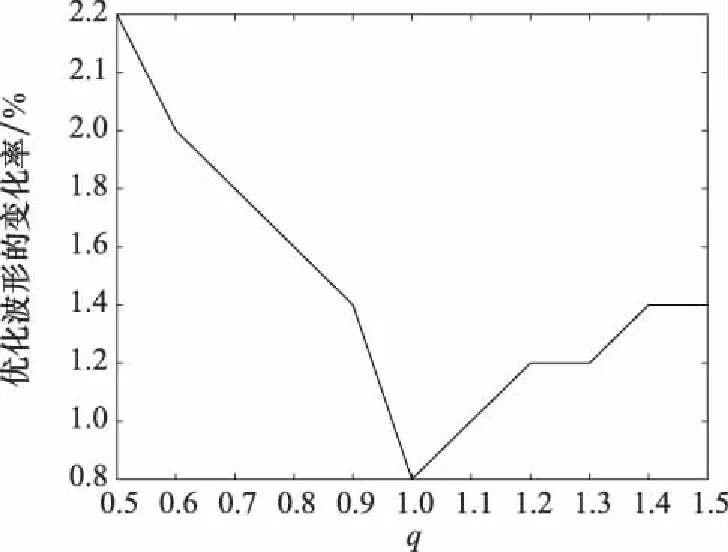
图7 不同q值下的X(f)的变化率Fig.7 Change ratio of X(f) under different q

3.3 关于增减率的分析

为了进一步探究MS的性能,设置参数和来讨论互信息谱密度和信干噪比谱密度之间的增减性,和的定义如下所示:

(20)

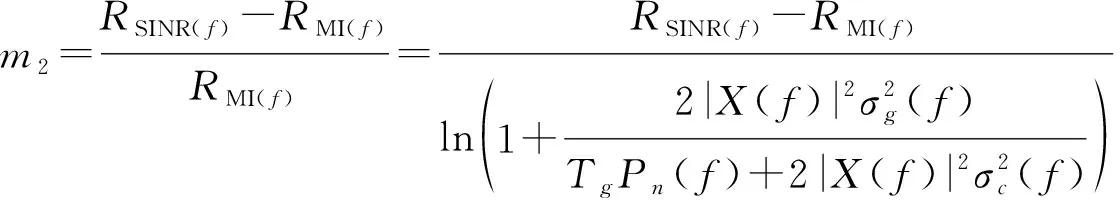
(21)

令∈[0,1],绘制式(20)和式(21)的曲线,如图8所示。由图8可见，互信息谱密度和信干噪比谱密度有着相似的增减率,最优发射波形形状基本不会发生变化。也就是说，改变、值时,MS可以实现不同权重的互信息或信干噪比优化波形,使得信号模型在雷达目标检测或识别性能方面达到各自的最优状态。

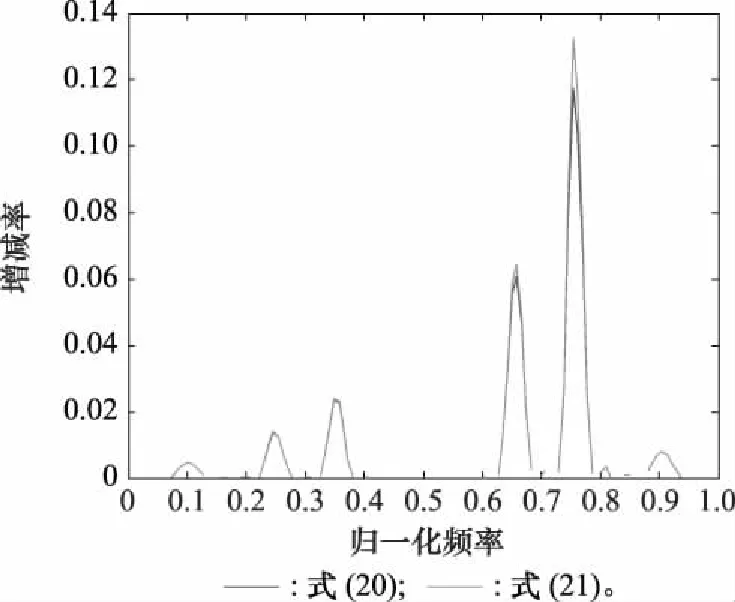
图8 互信息和信干噪比谱密度的增减率Fig.8 Gradient ratio in spectral density of mutual information and SINR

4 结 论

本文提出了一种MS下的波形优化设计方法,该方法综合考虑了目标与回波信号之间的互信息与信干噪比。由于互信息谱密度和信干噪比谱密度存在一定的指数关系,MS既可最大化互信息又可最大化信干噪比值。当改变、值时,优化波形的特征参数属性不变,通过改变、的取值,MS下的雷达信号模型可以实现多种模式和多种任务工作。最终,系统通过一次或较少次数的观测数值完成目标参数估计、检测或估计性能的分析,为雷达波形设计朝着多种任务发展提供参考和依据。