基于逻辑回归算法的某公司Offer申请结果预测研究
2022-10-28王祖斌
王祖斌,王 鑫
(兰州职业技术学院 汽车工程与交通运输系, 甘肃 兰州 730070)
一、引言
我国改革开放以来,历经40余年发展,在政治、经济、国防、科技和民生等诸多领域都取得了举世瞩目的成就。国家的发展离不开科技,科技是推动现代社会发展的源动力。特别是近年来,国内科技公司如雨后春笋般遍地开花,其中不乏有很多国际知名企业,如华为、小米、腾讯、大疆和字节跳动等,在享誉海内外的同时也创造出一座座科技里程碑。这些公司为高级求职人才提供良好的晋升空间和广阔的发展前景,进入这些企业工作是求职者实现人生价值的理想途径之一。然而此类公司对人才的要求也比较严苛,在正式获得公司offer之前,往往要通过几轮考核,只有真正有实力的求职者才会被公司吸纳。由于事关自身发展,广大求职者通常会多手准备,在积极准备当前公司入职考核的同时,还会关注其他单位的招聘情况,以免耽误自己就业。目标公司的offer申请是否成功是广大求职者相当关切的问题。如何能够较为准确地预测某公司offer的申请结果,及时调整自身求职计划是具有一定应用价值的研究;从国家宏观角度考虑,也可为调整高级人才就业相关政策提供数据参考。
在参考数据样本特征变化的情况下,对事情的结果进行预测其实是典型的分类问题。解决此问题可以根据数据样本的分布情况采用不同的方法,例如,当数据样本是连续的,可以使用多重线性回归[1];如果数据样本满足二项分布,可以采用逻辑回归[2];若是Poisson分布则应该考虑Poisson回归[3];数据样本是负二项分布,负二项回归[4]则是较好的选择等。目前利用逻辑回归进行分类的应用研究很多,如在流行病学领域中就有不少相关的应用研究,可以利用逻辑回归探索某种疾病的致病成因,根据不同的致病因素对某种疾病发生的概率进行预测。如郭志恒[5]等学者使用逻辑回归等方法对脑卒中患者进行相关研究并构建脑卒中疾病的判断算法,以便在疾病发生前提供一定的预警参考。段振云[6]等学者针对高精度零件图像的亚像素边缘提出了一种依靠逻辑回归算法的边缘定位方法,该方法有效地补偿了由于光源强弱所导致的边缘定位误差等。逻辑回归的应用已经较为广泛,但用于预测申请公司offer是否成功的案例相对较为稀少。本文构建了一个逻辑回归模型,该模型对目标公司offer申请的历史考核数据进行学习后,便可以大致掌握考核成绩与录取结果间的相关规律,从而能够较准确地通过新的考核数据来判断某职位的申请结果,是一项可以落在实处的研究课题。
二、理论建构
(一)逻辑回归(Logistic Regression)
在广义线性模型(Generalized Linear Model)领域中,逻辑回归与多重线性回归[1]存在许多相似之处,它们最大的区别其实就在于因变量的不同,所以可以将这两种回归归属于同一个范畴。逻辑回归模型的因变量既可以是二分类的,又能够是多分类的,但在实际使用时,二分类的情况既比较常用又较易解释,所以普遍使用逻辑回归来解决二分类问题。逻辑回归基本由以下几个部分构成,它们也是实现逻辑回归的几个基本步骤,分别为:
1.预测函数
尽管逻辑回归名称中包含“回归”二字,但如前所述,它其实是一种分类算法且主要用于解决二分类问题,可以用逻辑函数[7](也可称为Sigmoid函数),可以表示为:
(1)
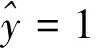
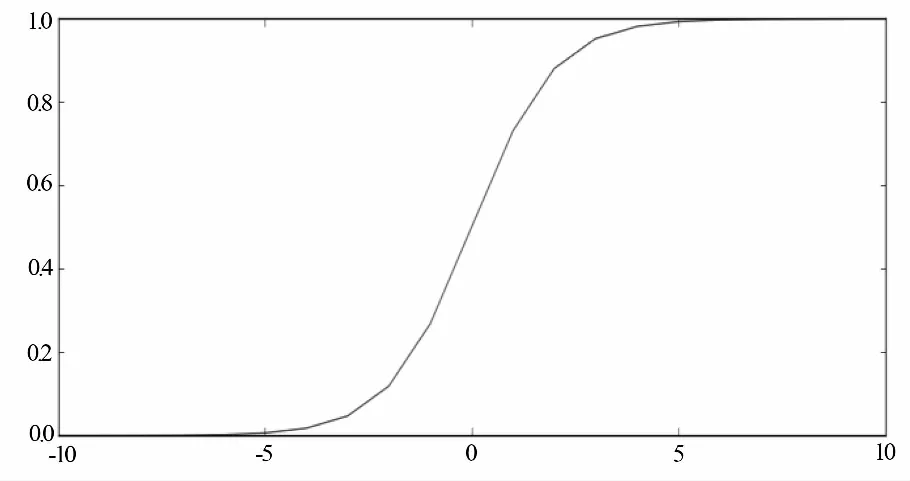
图1 Sigmoid函数曲线
所有使得θT·x=0的点,形成一条决策边界(Decision Boundary)[8]。例如当x含有两个特征x1和x2时,则有θT·x=θ0+θ1x1+θ2x2=0为一条直线,它将所有数据样本分割成两个部分,是一条线性决策边界。如图2所示。
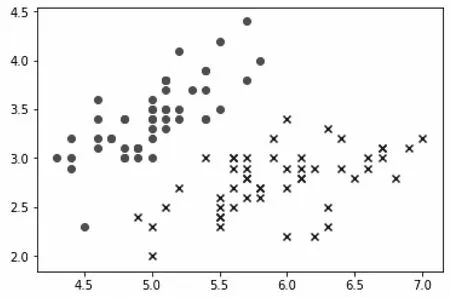
图2 二分类数据样本分布示例
其为鸢尾花数据集的样本分布状况,便可以利用线性决策边界将其分割成两个部分。如图3所示。

图3 线性决策边界
既然有线性决策边界,那么也存在非线性决策边界(Nonlinear Decision Boundary),其主要用于分割数据分布比较复杂的数据样本是非线性分布的情况,如图4所示。
图4 非线性数据分布散点图
它是由随机数生成的非线性分布形式的二分类数据。简单归纳一下上述内容,对于线性决策边界的情况,线性决策边界可以用公式(2)表达如下:
(2)
根据(2),可以构造预测函数g为:
(3)
其中,fθ(x)的取值为表达了预测结果为1的概率,由此可以推出当输入为x时的分类结果分别为类别1与类别0的概率为:
(4)
2.损失函数
接上一小节,将公式(4)整合为:
p(y|x,θ)=(hθ(x))y(1-hθ(x))1-y
(5)
对(5)取似然函数为:
(6)
其中m表示m个预测结果,其对数似然函数则为:
(7)
根据最大似然估计[9]来求解使l(θ)取最大值时的θ,如果使用梯度上升法进行求解便会求得满足需要的最优θ。若取
(8)
那么当J(θ)取到最小值时的θ则为满足要求的最优参数。
(二)梯度下降法
上一节,在梯度下降[10]法中,J(θ)不断趋向最小值的过程中,θ的更新过程可以用公式(9)表达:
(9)
简化表示为:
(10)
三、预测模型
本文在逻辑回归算法的基础上,针对求职者在申请某公司offer过程中为了最大化自己的边际机会,减少因为考核引起的求职成本,从而及时调整自己的就业规划等问题,利用某公司offer申请的历史数据,结合梯度下降法搭建了一个机器学习模型。该模型通过学习历史数据所蕴含的普遍规律所产生的算法模型可以根据申请者给定的具体输入数据样本给出合理的预测结果,其工作流程简述如下:
(一)通过两个数据特征进行二分类结果预测的逻辑回归架构
由于本文解决的实际问题是要根据输入的数据特征给出申请某个offer成功与否的结果,该结果只有两种,要么申请成功(可以用1表示),要么申请失败(可以用0表示),而要解决二分类问题,逻辑回归是比较有效的不二选择。对于需要分析学习的历史数据样本而言,这些数据的特征无论是在使用逻辑回归算法进行数据集学习的时候,还是面对随机陌生数据样本的时候,所要分析和处理的数据特征都是从数据文件中直接读取的,而非类似从图像数据样本中通过专门的过滤器进行提取,所以并不需要构建复杂的特征提取装置,也意味着其对于数据的处理并不需要巨大的计算开支,对于普通CPU来说已经能够完成目标,相应地也使得将本文方法所构建的机器学习模型部署在智能手机这样较为普及的弱算力设备上成为可能。本文针对具体的任务,根据公式(3)构建预测函数为:
(11)

(二)运用梯度下降法更新η
对于本文研究对象,将公式(8)推广至当前任务,则有:
(12)
其中m为2,实际上可以根据具体数据样本的特征项数量来确定m的取值,如果所涉及的具体任务不同、数据集数据样本的内容不同,可以因地制宜地继续进行普适化推广,这里不再赘述。求得当J(η)取得最小值时的η,这是一个不断更新的过程,需要算法持续对导入的公司offer申请历史数据进行学习,这个进程可以根据公式(10)表示为:
(13)
(三)实验分析与评价
1.实验环境
尽管本文用于实验的机器已经搭载了较高算力的GPU,但考虑到用于学习的数据样本仅含有两个特征项且不需要进行特征提取等复杂运算,也为了验证本文方法对于低算力设备的适应性,本文实验在不使用GPU的情况下,仅依靠CPU实施了具体实验。具体实验环境配置情况为:CPU是Intel i5-8300h@2.3 GHz(8核),内存8 G;操作系统采用Windows 10家庭中文版,Python 3.6开发环境,Jupyter NoteBook编辑器。
2.数据集
本文采用一个含有100个数据样本的文本文件作为数据集,其中每一行具体数据样本共同构成了整个微小规模数据集,作为本实验的训练数据集,每个数据样本包含两次考核成绩的特征项与是否申请成功的标签项。该数据集的具体结构及其包含的数据样本容量图5所示,其中显示了读取的前五个样本的具体内容,从数据列维度上来讲,前两列是两个具体的特征项,最后一列为标签项。整个数据集可以看成是一个100行3列的二维矩阵。随着研究的不断深入,该数据集可以无限扩充。为了保证训练效果,本文考虑了正、负样本数量均衡的问题,所参与训练的数据样本大体分布是比较均衡的,可以用散点图的形式将该数据集的分布情况较为直观地表示出来,如图6所示。
四、有效性验证
首先建立要件模块:(1)Sigmoid函数,它将输出结果映射到预测概率。(2)自定义向量点乘Model模块,它将返回输出的预测结果。(3)Cost函数将根据权重参数计算损失。(4)定义Gradient模块来计算各个权重的梯度方向。(5)定义Descent模块对权重持续更新。在本文实验中,根据比较迭代次数、损失以及梯度与阈值的差异采用了三种不同的梯度停止策略。在具体进行数据训练之前,通过使用Shuffle进行了一定的数据增强,以使得本文方法具有更好的稳定性。

图5 某公司offer申请历史数据集

图6 某公司offer申请历史数据样本分布图
(一)根据迭代次数更新权重
对于所有数据样本进行梯度下降训练,那么Batchsize设为100。将迭代次数设为5000次,学习率设为0.000001。经过0.83s的训练,权重更新完成,此时的模型损失为0.63,更新后的权重向量为array(-0.00027082,0.00715918,0.00367182),效果比较差,如图7所示。

图7 迭代5000次的训练结果
(二)根据损失值更新权重
设定阈值为0.000001时, 经过112649次迭代,耗时18.17s后,得到权重向量为array(-5.25282519,0.04820083,0.0421662),此时的损失已经大幅下降到了0.37,说明根据阈值更新权重的方式要明显优于根据迭代次数更新权重的方式,该方式训练结果如图8所示。

图8 根据设定阈值的训练结果
(三)根据梯度变化情况更新权重
当学习率为0.01且梯度小于0.05的情况下,算法才会停止训练,在经过6.89s且40760次迭代后的训练结果如图9所示。
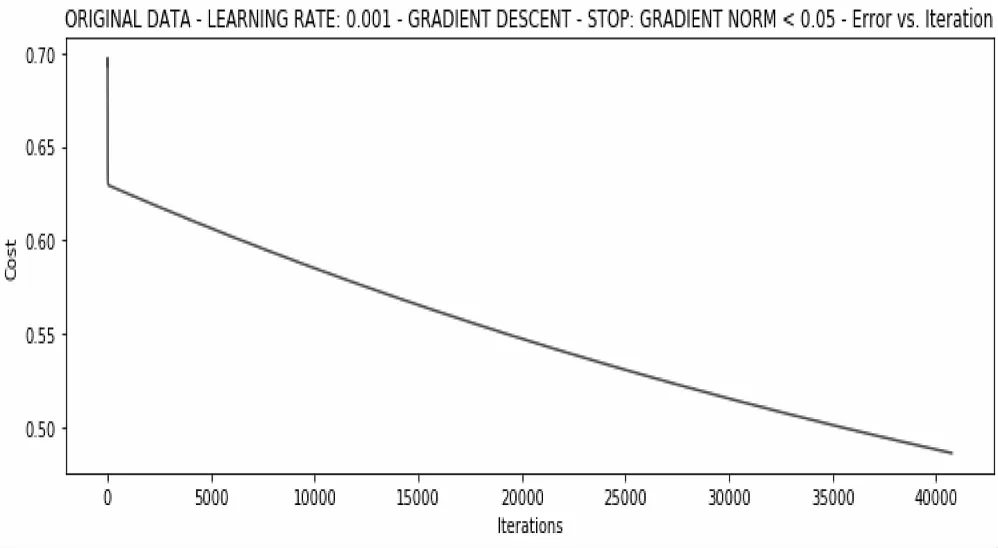
图9 根据梯度变化的训练结果
此时得到的权重向量为array(-2.40994356,0.02743917,0.01943823),损失达到了0.49,效果不及根据损失值更新权重的方式,但该方式的训练效率远超根据损失值更新权重,耗时仅仅是根据损失值更新权重方式的三分之一。
(四)进一步探索实验
在不使用数据增强的情况下,将学习率设定为0.001,采用随机梯度下降法对原始数据直接进行5000轮迭代训练,经过0.42s后,损失超过了1.59,效果很差,如图10所示。
其训练图像波动非常严重,梯度已有爆炸的迹象,十分不稳定,说明数据增强是非常必要的。
继续尝试对数据进行标准化处理,将数据按其特征项减去其均值,再除以它的方差。最后对每个数据特征项而言,所有数据都将汇聚在0的邻域范围内且方差值为1,再次训练在经过0.97s后停止更新权重,其结果如图11所示。

图10 对原始数据的5000轮迭代训练情况

图11 标准化数据的5000轮迭代训练情况
算法损失已经大幅降至0.38。那么更多的迭代次数会产生的结果如何呢?继续使用随机梯度,学习率依然是0.001,在耗时4.05s并经过了67336次迭代训练后,损失已经降至0.20,此时取得的权重向量为array ( 1.07426115,2.80678968,2.59430823),如图12所示。

图12 标准化数据的67336次迭代训练情况
在对若干个测试数据样本进行导入测试,可以得到的平均精度已经达到90%,已经满足实际应用的需要,即本文最终确定采用融合了数据增强、数据标准化、逻辑回归算法及随机梯度下降法并在满足梯度小于一个指定的微小阈值的情况下,经过充分数据训练后所得到的模型是一个具有实际应用价值的文件模型。
五、结语
本文在逻辑回归算法的基础上构建了一个机器学习模型,该模型充分利用梯度下降法,通过对某公司职位申请的历史数据进行充分学习,并达到了平均精度90%的测试效果。由于该类任务中的数据样本特征显著,也可以说特征一目了然,所以直接使用这些特征就可以完成数据训练,也并不需要高算力设备支持,因此可以将该方法部署在类似于移动手机这样的设备上,对于当下智能手机普及的时代而言,该方法针对某公司offer申请结果预测具有较好的实用价值。
