基于松鼠搜索算法的跨孔电阻率溶洞探测
2022-10-28梁森陈建华李宏涛罗威力罗盈洲艾姣姣廖伟
梁森,陈建华,李宏涛,罗威力,罗盈洲,艾姣姣,廖伟,
(1. 中建四局第一建设有限公司,广东 广州 510800; 2. 广州大学 土木工程学院,广东 广州 510006)
0 引言
近年来,中国城市化进程加快,基建工程项目越来越多。在岩溶地区修建建筑物易造成地基失稳、地表塌陷等危害,且该危害往往具有突发性和不可预测性。因此,提前探测出地下溶洞并加以处理,对建筑物施工和运营安全具有重要意义。常用的地下溶洞探测方法有电阻率法[1-2]、瞬变电磁法[3-5]、地震波法[6-7]等。20世纪90年代后,日本学者提出了跨孔电阻率法[8-9]。跨孔电阻率法的反演算法常采用基于Tikhonov正则化的灵敏度迭代法,但研究发现该方法对初值、噪声敏感,且容易陷入局部最优,导致反演结果失真[10]。
群智能算法是通过模拟某种生物群体的某一行为而实现的一类基于群体搜索的智能优化方法,它的优点是全局搜索能力强、无需灵敏度信息、对初值不敏感。比如粒子群算法[11](PSO)、云模型果蝇算法(CMFOA)[12]、JAYA算法[13]、松鼠搜索算法(SSA)[14]等。本文通过数值算例对比分析,选出了4种算法中性能最优异的算法——松鼠搜索算法,提出一种基于松鼠搜索算法的跨孔电阻率溶洞探测方法,以改善传统算法的缺陷,提高反演精度。通过构建小型、大型和串珠状充水型溶洞这3种工况的地下溶洞模型,分析对比Tikhonov正则化的灵敏度迭代法和松鼠搜索算法在溶洞位置定位、溶洞轮廓、多解性等的反演效果;通过室内物理模型和现场实验,验证松鼠搜索算法在跨孔电阻率溶洞探测领域中的实际应用效果。
1 跨孔电阻率溶洞探测基本原理
1.1 基本原理
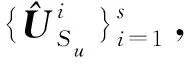
(1)
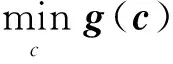
该优化问题为典型的非线性最小二乘优化问题,一般采用灵敏度迭代法进行求解,即先对公式(1)的R(c)进行Taylor展开,从而得到线性化的优化问题,然后引进Tikhonov正则化求解。该求解过程写成迭代形式为
(c-ck-1))‖2+λ‖c-ck-1‖2}=ck-1+
k=1,2,…,itermax。
(2)

其中u=[u1;u2;…;un],包含了所有节点电势;itermax为最大迭代次数。
由上可知,传统的基于Tikhonov正则化的反演算法需要对初值集合c0进行估计,也没有脱离局部最优解的数学手段。因此,该反演算法对测量噪声敏感,容易陷入局部最优解,最终导致反演结果与实际相差较大。
1.2 观测模式

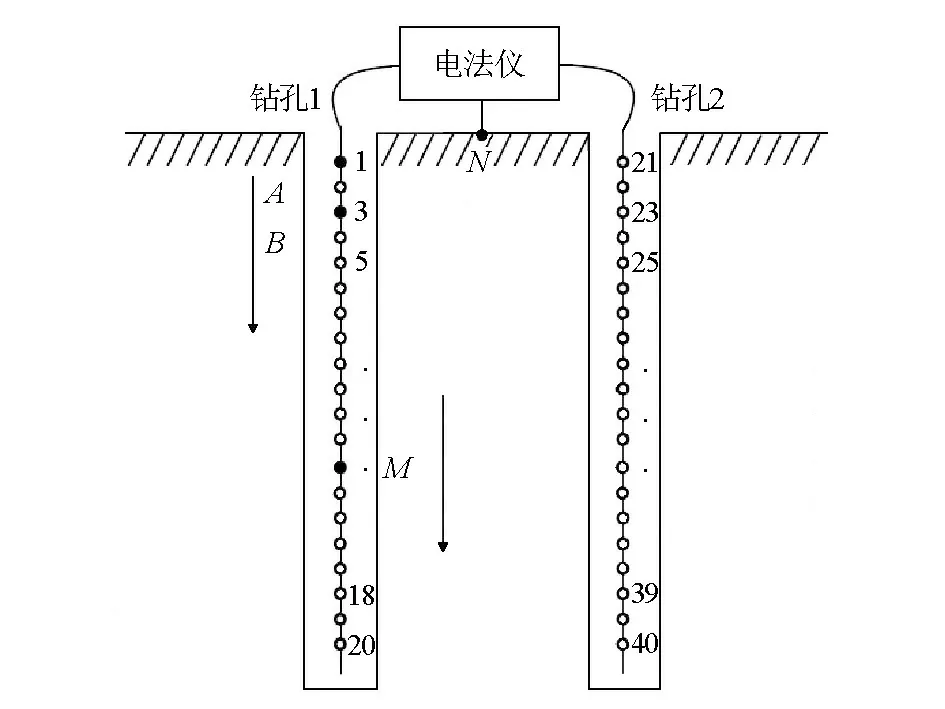
图1 观测模式示意Fig.1 A sketch of observation mode
2 松鼠搜索算法
2.1 方法原理
为了解决基于Tikhonov正则化的灵敏度迭代法存在的缺陷,本文引入松鼠搜索算法构建跨孔电阻率溶洞探测反演方法以提高反演精度。松鼠搜索算法(SSA)是Mohit Jain于2018年提出的一种基于松鼠的动态觅食行为的群体智能优化算法[14],该算法平衡了全局和局部搜索能力,在保证精度的情况下寻找全局最优解。松鼠搜索算法的核心包括以下6个步骤。
1) 随机初始化松鼠位置。假设森林中有NP个松鼠(FS),其中,FSi,j表示第i只松鼠的第j维。森林中每只松鼠的初始位置由下式分配:
FSi=FSL+U(0,1)·(FSU-FSL) 。
(3)
式中:FSU和FSL是FSi的j个维度的上下限向量,U(0,1)是[0,1]范围内的随机数。
2) 松鼠适应性评估。由目标函数计算出每只松鼠FS的适应值,相应的值存储在数组f中:
(4)
式中:f(·)是目标函数,用于计算每只松鼠的适应值;n是松鼠FSi的维度;NP是种群数量。
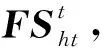
4) 产生新松鼠位置。在松鼠动态觅食过程中,可能会出现3种情况。
情况1:在橡树上的松鼠可能会向山核桃树移动:
(5)
情况2:正常树上的松鼠可能会向橡子树移动,以满足它们的日常能量需求:
(6)
情况3:一些松鼠在正常的树上已经吃了橡子坚果,它们可能会向山胡桃树移动,以便储存山胡桃坚果,以便在食物短缺时食用:
(7)
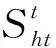
5) 判断季节性监测条件。季节变化显著影响松鼠的觅食活动,与秋天相比,气候条件迫使它们在冬天不那么活跃。在算法中引入了一个季节性的监测条件,可以防止算法陷入局部最优解。模拟行为步骤如下。
t=1,2,3,…,itermax。
(8)
c.如果季节监测情况属实,将无法在森林中寻找最佳冬季食物来源的松鼠随机迁移。
6) 冬季末随意搬迁。松鼠在冬季无法在森林中寻找最佳食物来源,但仍然存活下来,它们可能会向新的方向觅食。在建模中引入这种行为可以增强算法的探索能力,可同过方程式模拟:
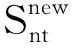
(9)
式中的Lévy(n)是研究人员用来提高各种元启发式算法的全局搜索能力的一种强大的数学工具[15]。
2.2 基于松鼠搜索算法的反演
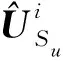
(10)
FS=c=[c1,c2,…,cN]T。
式中:f为目标函数值即松鼠的适应值;s为电极方案数量;FS表示松鼠位置。在本文中,停止准则设置为最大迭代次数iter≥itermax。图2为采用松鼠搜索算法进行溶洞反演的流程。

图2 松鼠搜索算法反演流程Fig.2 An inversion flowchart of the squirrel search algorithm
3 数值算例
3.1 不同智能算法计算结果对比
为了检验松鼠搜索算法在跨孔电阻率溶洞探测的算法优势,本文选取了3种常用的群智能优化算法进行对比,即:云模型果蝇算法(CMFOA)、粒子群算法(PSO)和JAYA算法。采用二维的四节点矩形单元进行网格划分,并采用Matlab编写程序和计算。图3中红色框线是溶洞真实位置轮廓线。模型参数为:孔间距5m,孔深度10m,单孔电极10个,围岩电阻率263Ω·m,溶洞电阻率10Ω·m,溶洞坐标为(1.75m,2.75m)。所有群智能算法的参数设置一致,最大迭代数量itermax=100,种群数量NP=250,最小电阻率值ρmin=10Ω·m,最大电阻率值ρmaxρmax=263Ω·m。
图3、图4对比了4种群智能优化算法的反演计算结果。图3显示,只有松鼠搜索算法(SSA)可以精确地反演出溶洞的位置和大小,其他算法均不能反演出溶洞真实位置。从图4可以看出,云模型果蝇算法(CMFOA)和粒子群算法(PSO)虽均已收敛,但都陷入局部最优解;JAYA算法虽然未陷入局部解,但收敛速度弱于松鼠搜索算法;松鼠搜索算法的收敛速度快,最终的适应值趋近于0(即趋近于精确解)。综上,相对于其他3种常用的群智能优化算法,松鼠搜索算法收敛速度快且可以跳出局部最优解,精确度高。
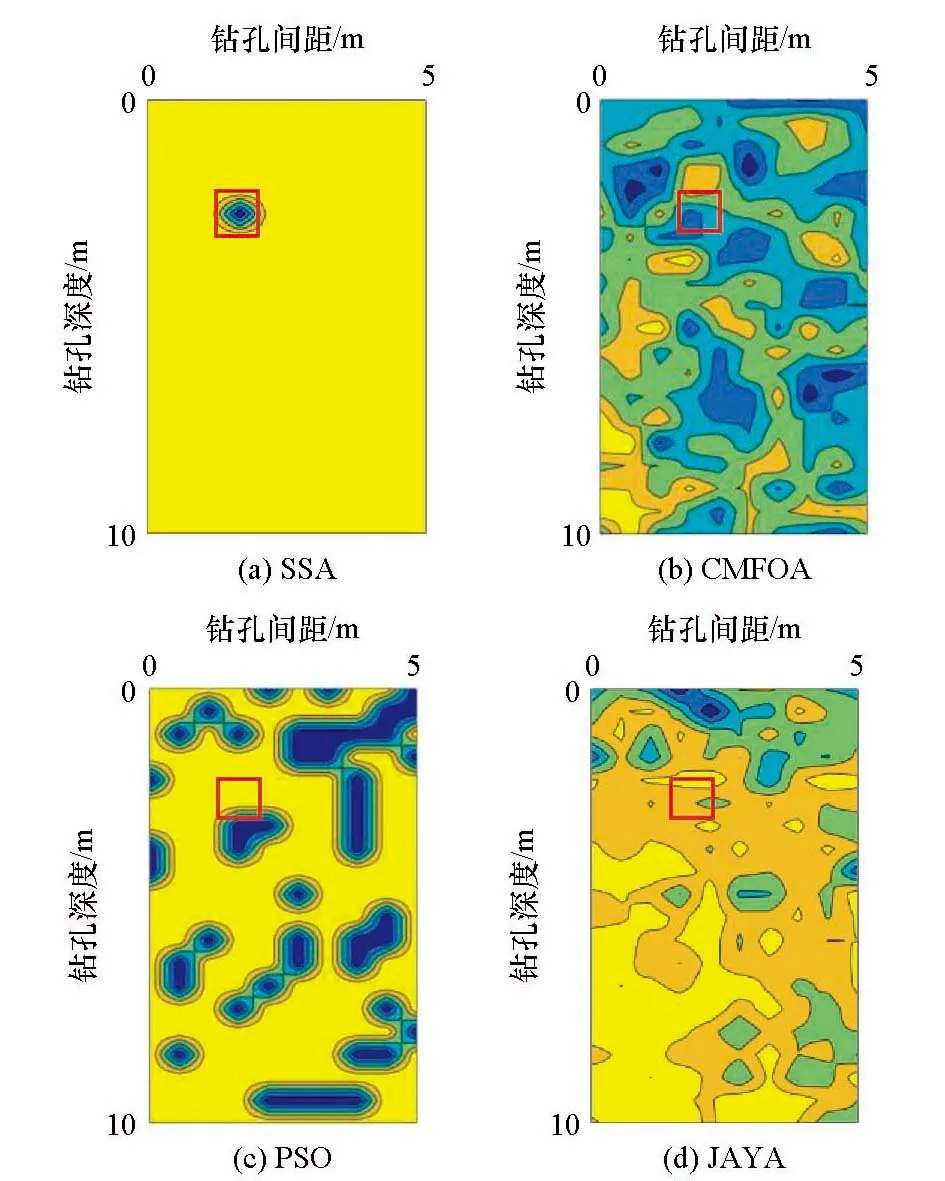
图3 不同智能优化算法反演结果Fig.3 Inversion diagrams of different intelligent optimization algorithms

图4 不同智能优化算法的反演迭代结果Fig.4 Inversion iterations of different intelligent optimization algorithms
3.2 松鼠搜索算法与灵敏度迭代法计算结果对比
为了对比松鼠搜索算法与灵敏度迭代法的反演精确度,设计了3种数值算例,分别是小溶洞模型、大溶洞模型和串珠状溶洞模型(小溶洞尺寸为2m×3m,大溶洞尺寸为3m×4m,串珠状溶洞为小溶洞和大溶洞呈串珠状排列的两溶洞模型)。模拟区域范围为20m×10m,单孔布置20个电极,围岩电阻率为263Ω·m,溶洞电阻率为10Ω·m。松鼠搜索算法初始参数设置为:最大迭代数量itermax=100,种群数量NP=250,最小电阻率值ρmin=10Ω·m,最大电阻率值ρmax=263Ω·m。
图5给出了3种溶洞(图中红色线框)的灵敏度迭代法反演结果。可以看出,灵敏度迭代法可以清晰地反演出小溶洞和大溶洞的形态和位置,其中大溶洞反演结果在电极附近显示较多假异常体;在反演串珠状溶洞时,探测区域的中部出现了一个大块假异常体,探测结果显示了3个独立的溶洞。灵敏度迭代法的反演结果呈现出了多解性,严重影响了溶洞的准确定位和形态的辨别。

图5 灵敏度迭代法反演结果Fig.5 The inversion results of the sensitivity iterative method
图6为3种溶洞的松鼠搜索算法反演结果。从图中可以看出:对3种溶洞,反演结果均可以精确地定位出溶洞位置,其形态轮廓基本对应,并且几乎没有大块的假异常体。这表明反演结果没有多解性,可以提供精确的溶洞识别结果。
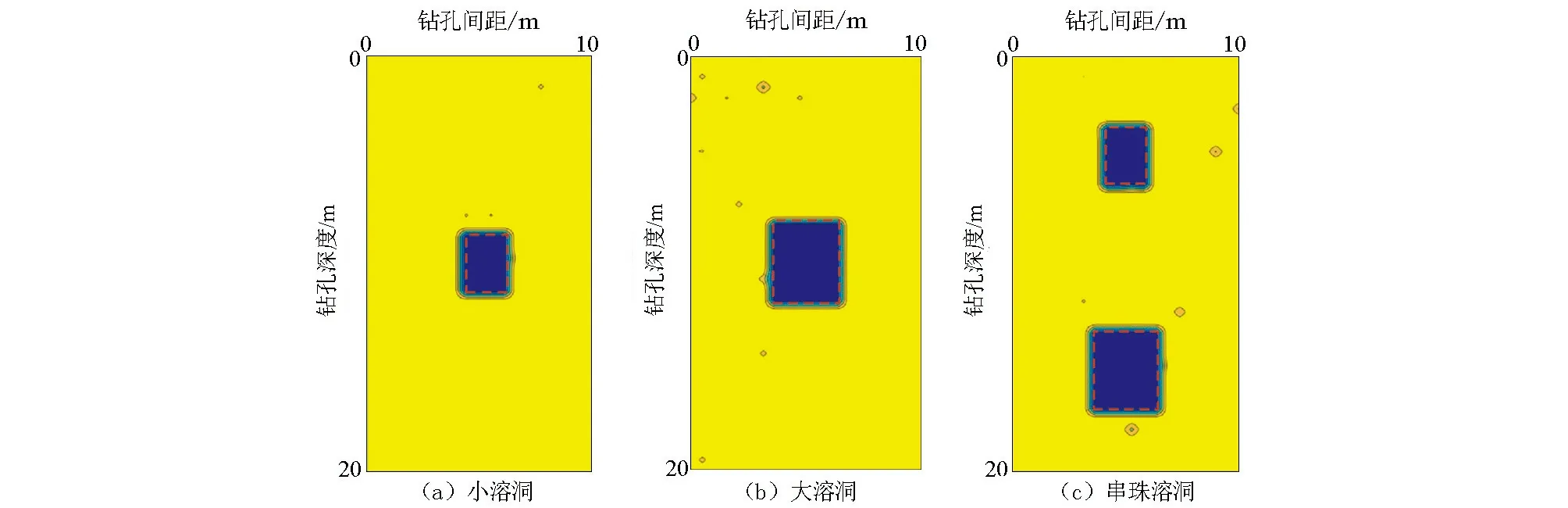
图6 松鼠搜索算法反演结果Fig.6 The inversion results of the squirrel search algorithm
图7为松鼠搜索算法的迭代曲线,可以看出算法基本在第10步左右就已经收敛,收敛速度极快且精确度高。

图7 松鼠搜索算法迭代曲线Fig.7 Iterative graphs of the squirrel search algorithm
表1总结了松鼠搜索算法和灵敏度迭代法的反演结果。整体上看,灵敏度迭代法虽可以很好地定位小溶洞和大溶洞的位置,却无法准确定位串珠状溶洞,而松鼠搜索算法可以精准地定位出3种溶洞的位置。在溶洞轮廓反演方面,灵敏度迭代法虽可以较好地反演小和大溶洞的轮廓却无法很好地反演出串珠状溶洞的真实轮廓,而松鼠搜索算法可以精准地反演出3种情况下溶洞的真实轮廓。在反演多解性方面,灵敏度迭代法的反演结果在测量电极附近显示出较多假异常体,尤其在反演串珠状溶洞时,探测区域的中部出现了大块假异常体,严重影响溶洞的准确定位;与之相比,松鼠搜索算法可以有效抑制反演的多解性,反演结果精确,假异常体少。

表1 反演结果对比Table 1 Contrast of inversion results
综上所述,无论是溶洞位置定位还是溶洞轮廓反演的表现,松鼠搜索算法均优于灵敏度迭代法。同时灵敏度迭代法的反演结果呈现多解性,而松鼠搜索算法则能有效抑制多解性,使得反演结果的精确度显著提升。
4 实验验证
室内模型实验采用国产集中式高密度电法探测仪,主要由多功能直流电法仪、电极转换器、高密度电缆、电源箱和电源组成(图8)。

图8 高密度电法探测仪Fig.8 High-density electric detector
图9为制作的室内溶洞物理模型,原型与模型的几何相似比G为10。表2为各几何因素原型尺寸与模型尺寸的对照。基于相似性原理,模型需要满足以下两个方面的要求:① 几何因素比值统一为10,几何因素包括地质体的大小、埋深、位置、电极位置等;② 各电性不均匀体的比值参数须与实际地质条件一致。采用粉质黏土模拟灰岩,其电阻率约为263Ω·m;采用边长为0.1m的六面体空心导电铁块模拟充水溶洞,20 ℃(常温)时的电阻率为78×10-8Ω·m;采用边长为0.2m 的六面体混凝土块模拟充气溶洞,20 ℃(常温)干燥时的电阻率约为 1000Ω·m。

图9 溶洞模型Fig.9 Cave models

表2 各几何因素原型尺寸与模型尺寸对照Table 2 The comparison of the prototype dimensions of each geometric factor with the size of the model
本次实验主要采集电流数据和电压数据。按新型的四极观测模式跑极并记录电势差数据,将每种A-B组合下测量到的10次电流值加和后取平均值,该平均值即为同种输入输出A-B组合下的电流值。由于仪器的测量结果只能反映出一个正值电流,实际上输入输出的电流值应互为相反数,故将上述的平均值取相反数,其相反数即为输出的电流;另一方面,也是为了确保边值问题上解的存在性,所有输入输出的电流总和必须为0。电势差是每个测点相对于中间测点N的电势差,在进行反演计算时,需要在Matlab上模拟出中间测点N的电势值,然后用测量的电势差值加上N点的电势值即可近似为每个测点的电势。有限元方法下边界条件的方程为
(11)
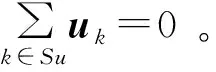
对电势值具体的处理方式为:同种输入输出组合下的电势值加和并求平均值,然后用每个电势值减去所求的平均值。
模拟区域设置为1.5m×1.0m;松鼠搜索算法参数设置为itermax=500;充水溶洞模型参数设置为:NP=250,ρmin=0.1Ω·m,ρmax=263Ω·m;充气溶洞模型参数设置为:NP=250,ρmin=263Ω·m,ρmax=1000Ω·m。将处理好的电流和电势差数据导入松鼠搜索算法的跨孔电阻率探测反演程序进行反演计算,通过迭代反演得到最终的反演成像结果。
图10为充水溶洞模型的反演结果和迭代曲线,图中红色方框表示导电铁块的实际埋设位置。反演结果显示:在框线内有一个大小为0.05m×0.1m、电阻率为0.1Ω·m的低阻体,此外,在框线外有少量的假异常体。从迭代曲线图可以看出,适应值在第200次迭代反演计算中趋于0,说明反演结果已收敛,收敛速度较快。反演结果基本与实际情况相符。
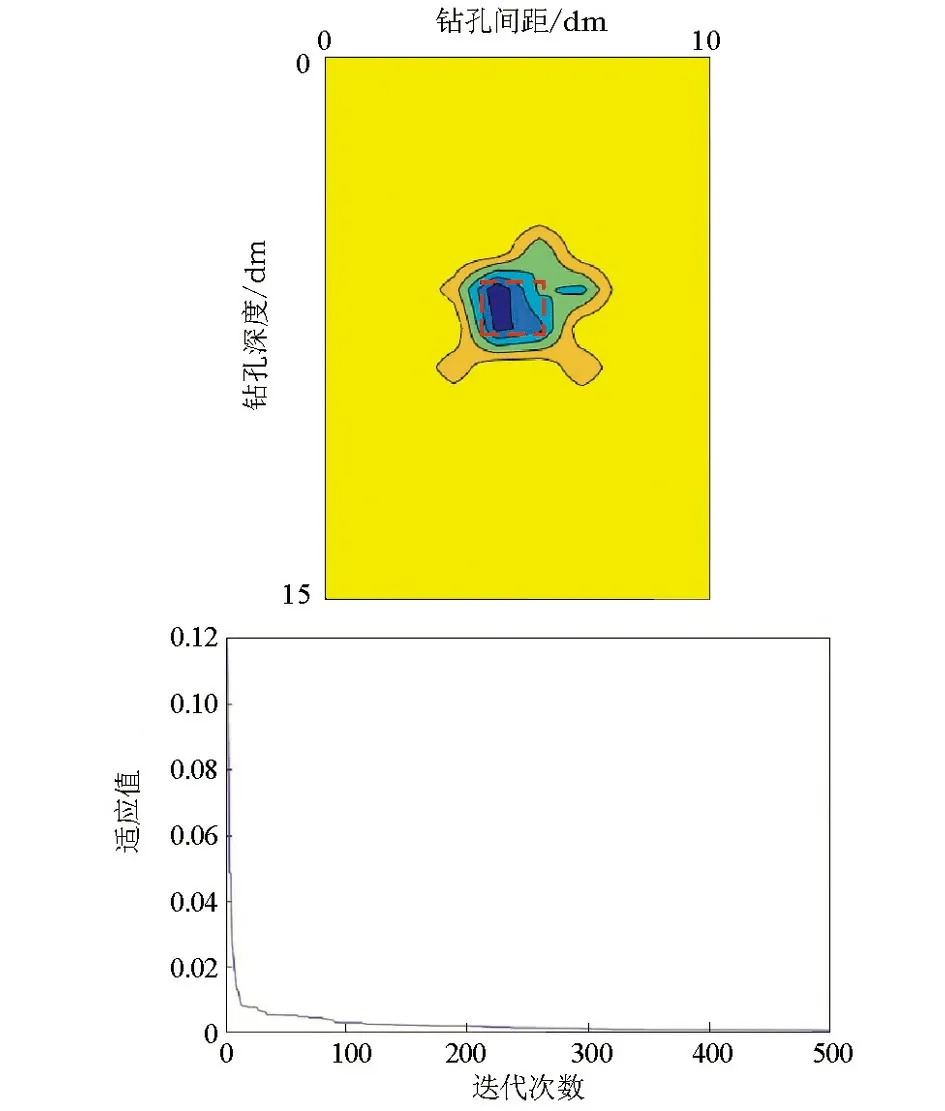
图10 充水溶洞模型反演结果(a)与迭代曲线(b)Fig.10 Inversion results of water-filled karst cave model (a) and iterative curve (b)
图11为充气溶洞模型的反演结果和迭代曲线,图中红色方框表示混凝土块的实际埋设位置。图11a显示框线内有一个0.05m×0.05m、电阻率值为1000Ω·m的高阻体,框线外有少量的假异常体。图11b与图10b同样,适应值也在第200次迭代反演计算中趋于0。
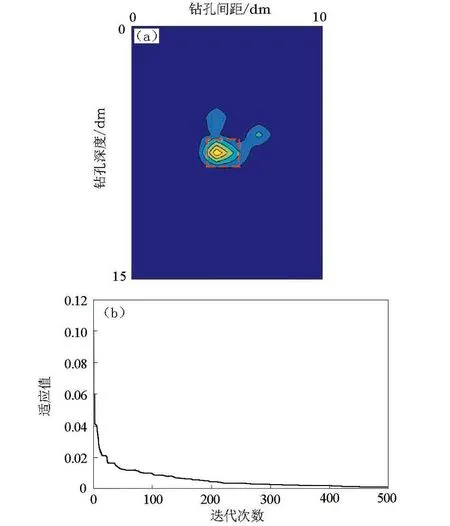
图11 充气溶洞模型反演结果(a)与迭代曲线(b)Fig.11 Inversion results of the gas-filled cave model (a) and iterative curve (b)
综上,不管是充水还是充气的溶洞模型,在考虑有测量误差、模型误差和背景土体非均质性的影响下,反演结果都基本反映了室内模型的真实情况。
5 实际工程应用
为了进一步检验改进观测模式和反演方法的有效性,在广州市花都区花山镇平西村、新和村美华航空电子研发项目工程建设工地开展了溶洞探测现场实验。根据钻探揭露,施工场地下伏石炭系灰岩,大部分地段溶洞极发育,勘察中钻遇溶洞和土洞的钻孔有47个,见洞率达32.6 %,见溶洞层数为1~2层,为岩溶强发育区;大部分溶洞顶板较薄,多为串珠状,半充填—全充填,部分为空洞,充填物为软塑状或流塑状黏性土及少量风化岩块。
根据地质调绘、物探和钻探资料,测区内大致有6类不同介质的地层:素填土、粉质黏土、砾砂、溶洞、中风化石灰岩和微风化石灰岩,地电断面大致分为5层,详见表3。溶洞与围岩存在较大的电性差异,具备直流电法勘探的物性前提。溶洞、软弱夹层、溶沟、富水带等强溶蚀带为此次探测的目标体。

表3 测区视电阻率分布Table 3 The visual resistivity distribution table of the measured area
现场实验选取了2个钻探好的孔位,两孔相距约10m,井口高程相差0.25 m,钻探深度分别为23 m和20 m(表4)。分析钻探结果可以推知,在钻孔深度13.2~18m处存在溶洞(充填粉质黏土),围岩为微/中风化石灰岩。两孔之间的具体溶洞分布情况未知。
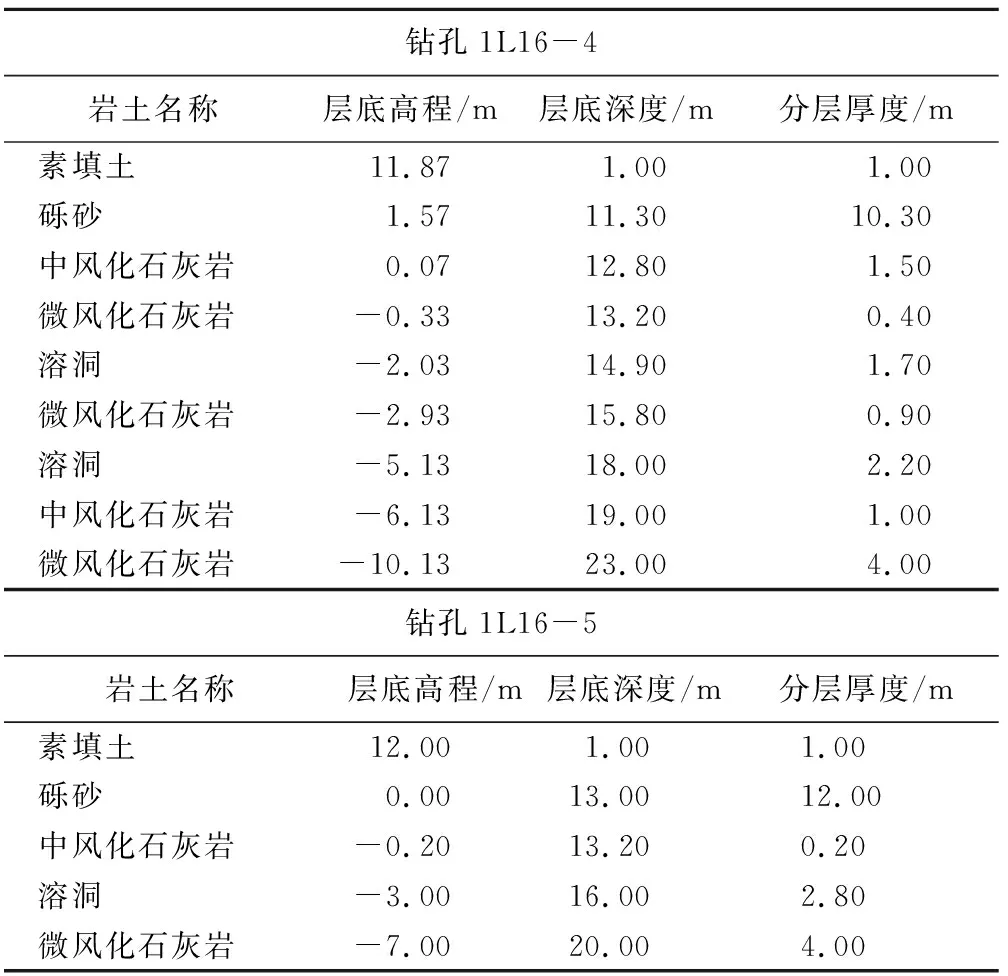
表4 钻孔柱状图部分结果Table 4 Summary of the results of the drilling bar chart section
根据新型的四极观测模式测量电势差数据,将得到的电势差数据导入反演程序中,模拟区域设置为20m×12m,单孔电极数量为16个。松鼠搜索算法参数设置为:itermax=1000,NP=250,ρmin=1Ω·m,ρmax=3000Ω·m。
钻孔剖面的基于松鼠搜索算法的反演成像结果见图12。从迭代曲线图(图12d)可以看出,适应值在第200次迭代反演计算中趋于0,说明反演结果已收敛,收敛速度较快。图12a显示:在深度0~3m范围电阻率较高,可以推断属于素填土层,含水率较低所以电阻率较高;在深度3~12m范围电阻率值大幅降低,推测此深度范围位于地下水位或发生土层电性改变,引起电阻率升高,部分区域的电阻率较高推测可能是孤石引起;在深度12m以下的探测范围内电阻率普遍升高,可以推测到达了石灰岩层;在深度14~18m范围内,出现了3个电阻率值与上层土相近的孔洞,推测石灰岩层出现了串珠状的溶洞,充填物为上层土(粉质黏土),这与2个孔位的钻探结果显示的深度13.2~18m处有串珠状溶洞基本相符。
由于剖面中部的溶洞是否存在未知,为进一步验证算法反演结果,在两孔中间打一个验证孔,其柱状图如图12b所示。将反演图与验证柱状图对比发现,在剖面中部位置确实存在溶洞,且溶洞位置与反演结果预报位置基本吻合。
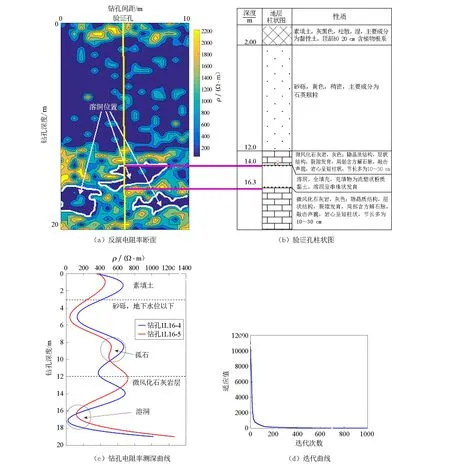
图12 现场实验反演结果Fig.12 Inversion results of field experiment
综上所述,基于松鼠搜索算法的反演结果与钻探结果基本吻合。
6 结论
1) 数值算例的反演结果表明:对比粒子群算法(PSO)、云模型果蝇算法(CMFOA)和JAYA算法,基于松鼠搜索算法的跨孔电阻率溶洞探测方法具有收敛速度快、精确度高、全局优化能力强的优势。
2) 数值模拟小溶洞、大溶洞和串珠状溶洞的反演结果表明:在溶洞位置定位、溶洞轮廓识别、多解性抑制方面,松鼠搜索算法均优于灵敏度迭代法。
3) 通过室内溶洞模型试验可知,基于松鼠搜索算法的跨孔电阻率溶洞探测反演结果基本反映了室内模型的真实地下情况。现场实验最终的反演结果与钻探结果对比分析,反演结果基本可以准确地反演出地下溶洞的真实位置和形态,进一步验证了基于松鼠搜索算法的反演方法实际工程应用效果。
