多分量重力梯度数据联合欧拉反褶积与软件系统设计
2022-10-28孙伯轩侯振隆周文月巩恩普郑玉君程浩
孙伯轩,侯振隆,周文月,巩恩普,郑玉君,程浩
(1.东北大学 资源与土木工程学院,辽宁 沈阳 110819;2.中国自然资源航空物探遥感中心,北京 100083)
0 引言
重力梯度数据是引力位数据沿坐标轴方向的二阶导数,具有分辨率高、抗干扰能力强的特点。近年来基于重力梯度数据的密度反演[1]、边界识别[2-3]和成像方法[4]等研究发展迅速。
在上述方法中,欧拉反褶积是一种能自动计算场源位置的方法,Thompson于1982年将欧拉反褶积拓展到重力异常数据中[5],但是在欧拉反褶积的应用过程中会产生发散解,降低计算精度,因此有必要改进方法,提高分辨率。许多国内外学者围绕该方法开展了研究并取得良好的效果:Cooper通过计算单个数据点的解和选择场源位置,提高了结果的准确性[6];Petar等拓展了Thompson[5]提出的构造指数的范围[7];Wang等[8]在欧拉反褶积计算中引入了奇异值分解技术,降低了噪声对计算结果的影响;Eric等[9]尝试将重力数据欧拉反褶积与震源边缘检测等方法结合,可以更清晰地显示细节;Zhang等[10]提出了利用重力梯度数据进行欧拉反褶积,提高了场源数据的解释精度;Majid等[11]进一步讨论了结构指数的使用,该参数能够减少地质体定位时的不确定性;周文月等[12]提出了不同高度观测数据的联合欧拉反褶积方法,拓展了欧拉反褶积的应用范围;侯振隆等[13]对重力梯度数据联合欧拉反褶积又做了进一步改进,避免了构造指数的选择和分量转换,提高了计算的精度。马国庆等[14]利用重力梯度张量及其导数改进了联合欧拉反褶积算法矩阵,降低背景异常差异的干扰。相对于重力异常数据的欧拉反褶积,使用重力梯度数据的方法对目标地质体具有更高的识别分辨率。
GeoProbe[15]、Geoquest[16]、GeoEast[17]等专业软件近年来发展迅速。许多国内学者在重磁处理解释软件架构与开发技术的自主研发方面做了很多研究:郑元满等[18]研发了针对金属矿勘探的重磁综合软件,利用协同交互操作提高了软件工作效率。陈靖等[19]设计了一种基于组件加插件的分层体系架构的重磁软件,实现多元数据集成分析解释。王浩然[20]基于重磁数据物性反演方法设计了一种卷积神经网络,降低了重力密度成像所需的训练量。张浩平等[21]用Visual C++6.0调用Matlab Engine,以Matlab脚本为核心开发了一种磁性数据的三维欧拉反褶积计算软件,为相关的软件开发提供了思路。从重磁数据处理解释软件的研发现状可知,当前已开发的商业软件较多,多数的功能较为完备和复杂,但不利于数据的高效解释和软件的二次开发。同时,在数据处理解释方法的研究中,绝大多数算法是通过编程语言单独开发脚本和函数实现的,缺少一个集成的软件平台。
可见,使用具有丰富函数库、可移植性高的语言,开发易用的可视化软件是十分必要的。这有利于降低方法二次开发与软件移植的难度,使研究人员减少对数据管理与可视化的开发成本,扩展解释方法的适用范围。因此,本文基于简洁实用的原则,利用Python语言及其函数库开发了一个支持数据/文件管理、二/三维可视化、边界识别、重力梯度数据联合欧拉反褶积等功能的软件系统,为今后的重磁数据解释研究提供技术支持。
1 方法原理
1.1 重力梯度数据联合欧拉反褶积
根据欧拉齐次方程的定义[13],欧拉反褶积公式如下:

(1)
式中:(x,y,z)与(x0,y0,z0)分别为笛卡尔坐标系中观测点和地质体中心坐标;f和B分别表示观测异常场和背景场;N为构造指数。将式(1)转化为向量积形式,即:

(2)
用引力位V在x、y、z方向的一阶导数Vx、Vy、Vz代替式(2)中各方向的f。因此,∂f/∂x、∂f/∂y、∂f/∂z在x方向分别转化为Vxx、Vxy、Vxz形式,y轴与z轴方向分量同理。由于求高阶导数影响计算精度,因此,利用式(3)计算引力位的三阶垂向导数:
(3)
最后,整理得出重力梯度数据联合欧拉反褶积公式:
(4)
重力梯度数据联合欧拉反褶积公式联合多个梯度分量建立方程组,将构造指数N与场源坐标一同视为未知数,有效地避免了选择构造指数所产生的系统误差,可以更准确地描述地质体空间位置。
1.2 基于方向总水平导数相关系数的边界识别方法
本文提出一种利用方向总水平导数生成的相关系数作为边界识别的方法:对方向总水平导数法(edge detector of total horizontal derivative,EDT)[22]归一化可得到归一化的方向总水平导数法(normalized edge detector of total horizontal derivative,NEDT)[3],计算EDT与NEDT的相关系数R,用此相关系数作为边界识别结果。公式如下:
(5)
其中:cov(EDT,NEDT)表示两种方法的协方差;D(EDT)与D(NEDT)分别表示两种方法的方差,故式(5)可改写为:
(6)
其中:EDTi与NEDTi分别表示窗口内第i个EDT与NEDT的值;N表示窗口内的测点数;R为EDT与NEDT结果的相关程度,无量纲,R∈[-1,1],R越接近-1,该处为地质体的边界的可能性越大,理想情况地质体边界处皆为极小值-1。本文称上述方法为基于方向总水平导数相关系数的边界识别方法(edge recognition based on correlation coefficient ofEDT,ERCC)。
1.3 基于相关系数边界识别约束的重力梯度数据联合欧拉反褶积
为降低重力梯度数据联合欧拉反褶积计算结果的发散性,可应用传统的水平梯度滤波、聚散度准则等方法[22]进行结果筛选,消除发散解。为了进一步提高筛选的精度,本文提出基于相关系数边界识别约束的重力梯度数据联合欧拉反褶积,首先通过ERCC预先划定地质体水平分布范围,然后使用重力梯度数据进行联合欧拉反褶积计算得到初步结果,之后删除划定范围外的发散解,最后联合传统筛选方法获取最终的可靠解。
除ERCC外,软件中内置的边界识别方法有:倾斜角法[23]、解析信号法[24]、总水平导数法[25]、归一化方向总水平导数法[3,26]和改进的方向总水平导数法[27]、方向总水平导数法[28]。使用模型试验来验证内置的边界识别方法的准确性,立方体模型在x轴与y轴水平方向分布范围为-400~400 m,埋深为200 m。边界识别方法效果如图1所示。

a—总水平导数法;b—方向总水平导数法;c—解析信号法;d—改进的方向总水平导数法;e—归一化方向总水平导数法;f—倾斜角法a—THDR; b—EDT; c—ASM; d—EEDT; e—NEDT; f—TILT图1 边界识别结果可视化(图中红色线框表示立方体边界)Fig.1 Visualization of edge detection results(the red wireframe in the figure indicates the boundary of the cube)
2 软件开发与功能
2.1 软件系统开发
软件是基于Windows10系统,其硬件配置为Intel Core i7-9750H处理器、8GB内存,利用Python语言的PyQt5.15.4、Numpy1.20.2和Matplotlib3.4.1等函数库开发的,软件结构图如图2所示。利用NumPy函数库实现边界识别与重力梯度数据联合欧拉反褶积的计算;利用Matplotlib函数库实现可视化功能,包括观测数据二维可视化、边界识别结果可视化、欧拉反褶积结果可视化等;软件界面与文件管理是通过PyQt5函数库实现的(主界面见图3),通过PyQt5还实现了重力梯度数据文件的选择、预览、输入、修改与储存等功能。

图2 软件结构Fig.2 Software architecture diagram

图3 软件主页面Fig.3 Main interface of software
在二次开发方面,为了方便算法的改进与软件功能的拓展,软件使用“信号槽”机制将界面与计算模块、可视化模块相连接,这种松散的耦合机制为二次开发提供便利条件。可利用“信号槽”机制将其他位场数据处理解释方法加载到软件中,增加软件的功能;也可将后续改进的算法直接写入软件计算模块替换当前算法;同时,由于对重力梯度数据联合欧拉反褶积算法、边界识别等计算模块进行了封装,可将其直接用于其他软件平台的后续开发。二次开发时只需重点关注算法代码的编写,降低了软件开发难度。
2.2 软件系统设计
软件系统以重力梯度数据联合欧拉反褶积计算为主要功能,使用直观的操作界面,得到可视化结果。基于边界识别结果约束的重力梯度数据联合欧拉反褶积方法的算法配准如下(见图4):①边界识别,划定地质体水平边界;②重力梯度联合欧拉反褶积计算,得到初步的计算结果;③最后对初步结果进行筛选,得出最终结果。根据算法流程和使用要求,软件系统应设计如下功能:①数据读取与管理功能;②边界识别功能;③重力梯度数据联合欧拉反褶积计算功能;④初步计算结果筛选功能;⑤结果可视化功能。
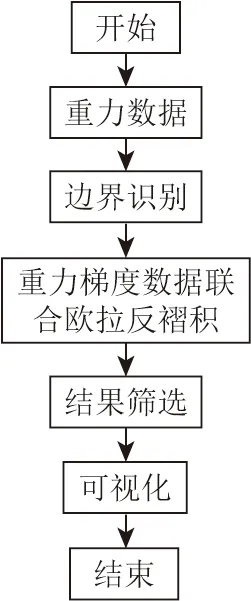
图4 算法流程Fig.4 Flow chart of algorithm
1)数据读取与管理功能:对数据进行操作时可能出现读取文件错误、数据可操作性低、数据不易查看的问题。为了降低误操作的可能性,设计数据预览窗口(图5),可在发现读取错误文件后及时退回文件选取窗口,重新选择数据文件。为了增加对读入数据的可操作性,在数据管理可视化窗口可以实现复制、粘贴、修改等操作(图6),文件导出功能可将修改后的数据以文本文档形式保存到计算机中(图7)。为了方便查看数据,根据重力梯度数据的获取方式,数据管理可视化窗口设计了分线功能(图8),以平行x轴方向作为测线布置方向,左上角下拉菜单可选择想要查看的测线。

图5 文件预览窗口Fig.5 File preview window

图6 数据操作窗口Fig.6 Data operation window

图7 文件储存路径选择窗口Fig.7 Window of file storage path selection
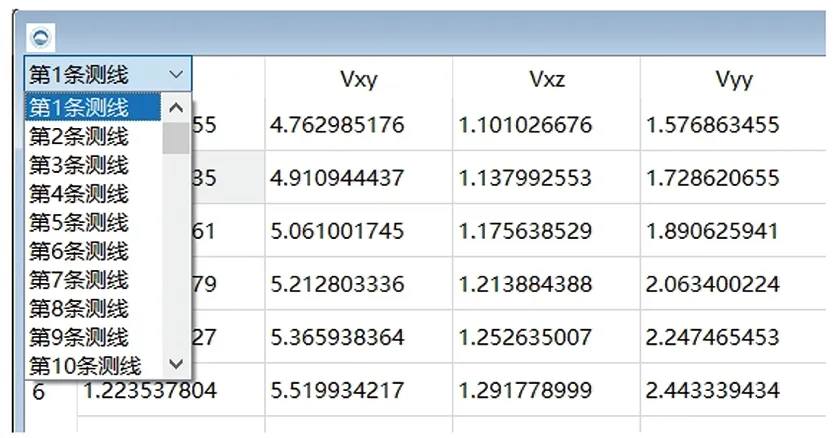
图8 测线切换窗口Fig.8 Line switching window
2)边界识别功能:引入边界识别方法并设置为联合欧拉反褶积计算的一个步骤,可以对地质体的平面分布具有初步的认识,为后续的计算结果筛选提供边界依据,减少误差。系统设置了包括总水平导数法、解析信号法、倾斜角法、方向总水平导数法、归一化的方向总水平导数法、改进的方向总水平导数法、倾斜角方向总水平导数法、相关系数法等边界识别方法,可以依据识别效果择优选用。筛选计算时只保留边界内的数据,降低后续筛选工作的计算量,提高计算效率。边界识别功能除了可以划定地质体边界范围外,也可将可视化结果单独以图片形式输出(图9)。

图9 软件输出的边界识别结果Fig.9 Edge detection result diagram from software
3)重力梯度数据联合欧拉反褶积计算功能:计算前要先确定地质体水平分布范围,为了方便对照边界识别结果,设计了如下的参数输入界面(图10)。只需要输入x与y轴方向的起止坐标作参数,即可划出形状为矩形的边界范围,简化了操作步骤。确定边界参数后,矩形线框会在边界识别可视化中显示(图11)。界面设置为交互式界面,边界参数可返回上一步修改,并实时更新图中线框位置,提高了便捷性。在输入计算窗尺寸与选择联合欧拉反褶积计算所需的梯度数据后,即可开始计算。参与计算的3个梯度数据分量可通过界面中(图11)的下拉框选择,软件依据式(4)预先设定选择的梯度数据分量为Vxz、Vyz与Vzz。软件的重力梯度数据联合欧拉反褶积计算公式与周文月等[12]提出的3个不同高度数据联合欧拉求解矩阵表达式格式一致,只是选取的数据类型不同,所以软件不仅能联合重力梯度数据进行联合欧拉反褶积计算,也可联合3种不同高度的重力异常数据进行联合欧拉反褶积计算。
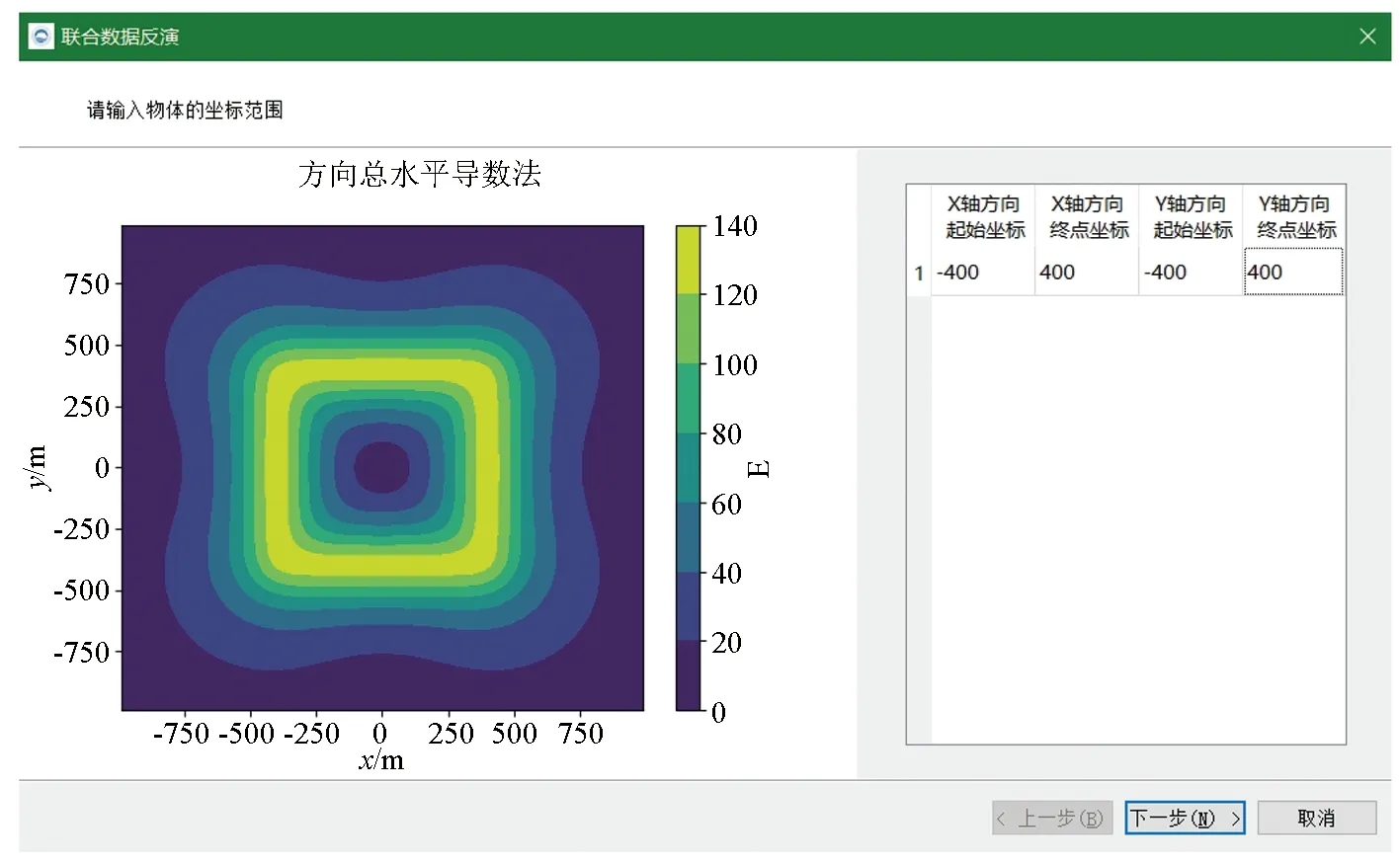
图10 划定地质体范围输入界面Fig.10 Delimit the geological body range input interface

图11 重力梯度数据联合欧拉反褶积计算参数输入界面Fig.11 Joint Euler deconvolution of multiple gravity gradiometry tensors calculation parameters input interface
4)结果筛选功能:当联合欧拉反褶积计算后的结果(图12)与地质体实际情况不相符时,需要通过有效的筛选方法筛选计算结果,使结果更加准确地描绘地质体位置与形状。软件内置的筛选方法有水平梯度滤波法[22]、聚散度准则[22]等(图13)。主要包括:①水平梯度滤波法:计算窗口内区域的水平梯度的模,并与用户输入的系数相乘得到筛选标准,删除水平梯度的模小于筛选标准的结果。用户输入的3个系数分别对应着先前重力梯度数据联合欧拉反褶积计算时选取的重力梯度分量。②主体异常距离准则:根据重力梯度数据联合欧拉反褶积计算的原理,计算结果的水平位置应该位于当前计算窗口范围内。对于超出计算窗口范围的点坐标,认定该计算结果误差较大,予以删除。③聚散度准则:根据重力梯度数据联合欧拉反褶积在地质体上方相邻多个滑动窗口所得到的计算结果相关性较强的特点,正确的计算结果应该比较密集的出现。过于分散的结果视为误差较大的结果,予以删除。用户可在筛选标准输入界面输入聚散度准则所需的作用半径与聚散度指数。④边界识别:重力梯度数据联合欧拉反褶积计算时依据边界识别结果可视化划定的范围作为筛选边界,删除边界外的计算结果,避免误差和屏蔽范围外的无效结果。筛选后的结果如图14所示。

图12 重力梯度数据联合欧拉反褶积初步计算结果Fig.12 Preliminary calculation results of joint Euler deconvolution of multiple gravity gradiometry tensors

图13 结果筛选标准输入界面Fig.13 Results filtering standard input interface

图14 重力梯度数据联合欧拉反褶积计算结果可视化Fig.14 Visualization of joint Euler deconvolution of multiple gravity gradiometry tensors results
5)可视化:为了可以直观地观察梯度数据的情况和边界识别结果,利用等势线图能够清晰地描绘数值的分布情况(图15)。图15显示的是x轴与y轴方向分布为-400~400 m、埋深为200 m的单立方体模型的重力异常数据与重力梯度数据等值线图,图中红色线框表示立方体模型的边界。在立方体边界处重力梯度数据的数值变化明显,重力异常数据可视化与模型实际位置相符。

a—Vxx分量;b—Vxy分量;c—Vxz分量;d—Vyy分量;e—Vyz分量;f—Vzz分量;g—Vz图15 重力异常数据与重力梯度数据等值线(图中红色线框表示立方体边界)Fig.15 Contour figure of gravity data and gravity gradient data(the red wireframe in the figure indicates the boundary of the cube)
利用三维散点的形式表现重力梯度数据联合欧拉反褶积计算结果的空间位置关系,简单且高效地将与x、y、z坐标相关的空间位置转化为易于观察的分布在三维空间的散点。同时,边界识别的结果也可置于三维散点图的上方(图14),使得结果展示得更为直观、全面。为了更准确地观察计算结果与正演模型相对位置关系,判断算法的分辨率,可视化模块中还具有添加辅助线框功能。软件可根据用户输入的坐标数据(图16)绘制立方体线框并显示在计算结果三维散点可视化中,辅助用户更好地对比正演模型与计算结果之间的区别,或辅助划定实测数据解释的地质体范围。
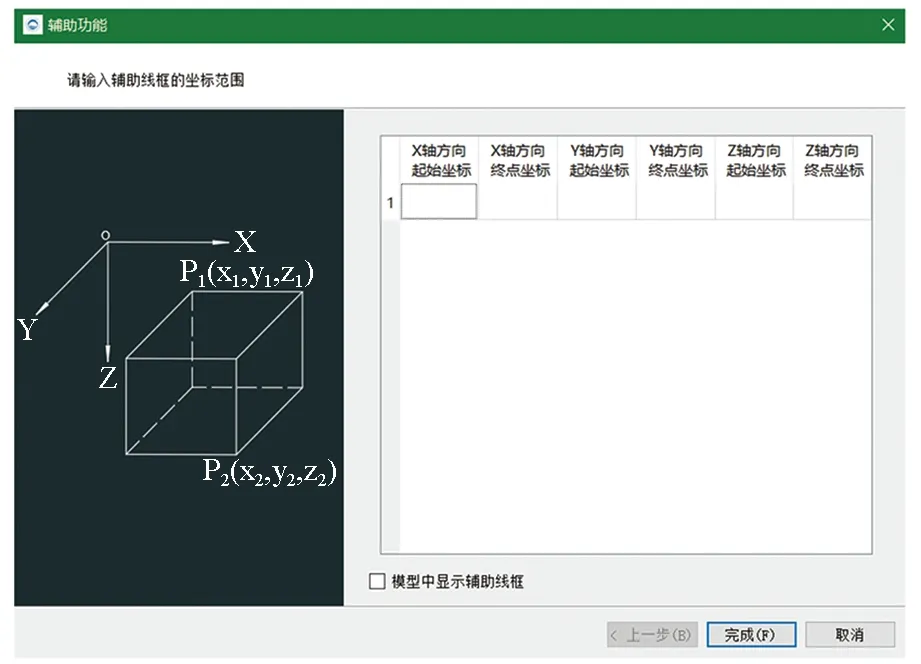
图16 辅助线框坐标输入界面Fig.16 Auxiliary wireframe coordinate input interface
3 数据试验
3.1理论模型数据试验
为了验证ERCC对不同深度地质体边界的探测精度,使用加入均值为0,标准差为0.01 mGal的高斯随机噪声的立方体模型数据进行试验。取x和y轴方向范围均为0~2 000 m、深度方向范围为0~1 000 m的空间,存在3个立方体模型,具体分布情况见表1。边界识别结果可视化如图17所示。

表1 立方体模型参数表Toble 1 Cube model parameters

图17 边界识别结果可视化(图中红色线框表示立方体边界)Fig.17 Visualization of edge detection(the red wireframe in the figure indicates the boundary of the cube)
地质体顶面埋深分别为100 m(A)、400 m(B)和700 m(C),由图17可知,随着地质体埋深的增加,相关系数变得越来越大。无地质体边界分布的区域相关系数范围为0.75~1,3个地质体边界的相关系数范围由A至C依次为:-0.75~-0.25、-0.25~0.25与0~0.5,埋深浅的地质体的相关系数小于深的,但都与0.75有一定差距。根据相关系数的极小值表示地质体边界的特性,埋深最浅的地质体A划定的范围为x轴向1200~1 850 m,y轴向150~850 m,最深的地质体C划定的x与y轴向的范围都是200~800 m,可见ERCC可以准确地识别出同一区域内不同深度的地质体的边界。同时ERCC也良好地压制了噪声的影响,结果中并未产生与实际情况不符的边界。
为验证基于相关系数边界识别约束的重力梯度数据联合欧拉反褶积的准确性和开发的软件的有效性,在笛卡尔坐标系下建立理论模型并进行模型试验。选取x和y轴方向范围均为-1 000~1 000 m、深度方向范围为0~1 000 m的空间,设地下有一个立方体形状地质体,长和宽为800 m,高为200 m,顶面埋深为200 m,测线间距为20 m,测线上测点间距为20 m,地质体剩余密度为1.0 g/cm3,并加入均值为0,标准差为0.01 mGal的高斯随机噪声。联合欧拉反褶积计算滑动窗口为19×19,水平梯度滤波法系数设为1,聚散度指数设为5、半径设为1.5倍测线间距。计算结果如图18所示,图中黑色线框为添加的辅助线框,表示模型所在位置。

图18 筛选后的重力梯度数据联合欧拉反褶积计算结果Fig.18 Screened results of joint Euler deconvolution of multiple gravity gradiometry tensors
由图18可知,筛选后的重力梯度数据联合欧拉反褶积的计算结果主要分布在200~280 m的深度范围,水平方向投影在立方体边界的位置上,在立方体顶点附近聚集着深度大于280 m的解。计算结果总体上分布在地质体的边界处,指示出地质体的分布范围与形状。通过模型数据试验,证明计算结果可以准确地标示出地质体的水平位置与埋深,验证了该方法的准确性与有效性。
3.2 实测数据试验
为了进一步验证方法和软件的适用性与准确性,采用文顿盐丘(Vinton Dome)地区的实测重力梯度数据进行试验。文顿盐丘位于美国路易斯安那州西南部与得克萨斯州交界处,地层以沉积岩为主[29]。该地区大陆架盆地的形成时间为新生代,地层以侵入岩为主。盐丘岩性主要为页岩和砂岩,剩余密度为2.2 g/cm3,盖岩的成分为石膏和硬石膏,该区域的重力梯度异常主要是其盖岩引起的。实测数据位于WGS84坐标系下,x轴代表EW方向,范围为440.5~444.5 km;y轴代表SN方向,范围为3 332.8~3 336.8 km。测区平均分布100条测线,每条测线平均分布100个测点。选取实测数据中Vxz、Vyz和Vzz这3个分量进行联合欧拉反褶积计算,计算滑动窗口为11×11,水平梯度滤波法系数设为1.5,聚散度指数设为6、半径设为1.5倍测线间距,结果见图19。
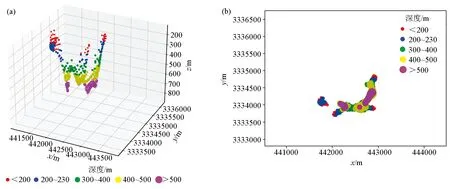
a—三维显示;b—z方向视图a—3D display; b—z-direction view图19 文顿盐丘数据联合欧拉反褶积计算结果Fig.19 Calculation results of joint Euler deconvolution of multiple gravity gradiometry tensors of Vinton Dome data
从图19a可以看出盖岩的埋深约为160~550 m,西侧盖岩埋藏较浅,埋深约为160 m;南侧盖岩埋藏较深,埋深约为550 m。从图19b可以看出岩盖整体呈现弧形,x与y轴向上分布范围分别为44 1700~442 900 m和333 380 0~333 480 0 m,盖岩的埋深由东南侧向东侧、南侧逐渐变浅。综上,软件计算结果与其他学者研究结果[30-31]一致,验证了软件计算的准确性。
4 结论
本文提出了基于相关系数边界识别约束的重力梯度数据联合欧拉反褶积,并开发了一种基于Python及其函数库的重力梯度数据联合欧拉反褶积可视化软件。提出的约束方法可以有效地减少欧拉反褶积的发散解,提高准确性;可视化软件具有数据/文件管理、二/三维可视化、边界识别、重力梯度数据联合欧拉反褶积等功能。经模型试验和实测数据试验,验证了计算的准确性和软件的有效性,且软件操作方法较为简单,可视化效果较好,为算法研究与应用提供了可靠的平台。同时,重力梯度数据联合欧拉反褶积算法已被模块化封装,方便后续研究进行二次开发。
致谢:感谢Bell Geospace Inc.提供文顿盐丘地区的实测数据。
