基于改进麻雀搜索算法的瑞利波频散曲线反演
2022-10-28孙旭计子琦杨庆义刘博政
孙旭,计子琦,杨庆义,刘博政
(1.山东电力工程咨询院有限公司,山东 济南 250014; 2.中国地质大学( 武汉) 地球物理与空间信息学院,湖北 武汉 430074)
0 引言
瑞利波是沿自由界面传播的一种弹性面波,由英国物理学家Rayleigh率先于1887年发现。在地震记录上,瑞利波通常成群出现,每一群面波按各自的频率散开,不同频率的瑞利波的传播特征反映了自由界面以下不同深度的信息,这一现象称为瑞利波的频散现象[1]。瑞利波的频散特性受地层各层的纵波速度、横波速度、密度、厚度的影响,其中以横波速度和厚度对瑞利波频散特性的影响最大[2],因此对瑞利波频散曲线进行反演可以较为精确地获取地层的横波速度和厚度信息。随着瑞利波理论的完善,瑞利波勘探已被广泛应用于浅地表地球物理工作中[3-4]。
目前广泛应用于瑞利波频散曲线反演的方法可分为线性和非线性方法。线性方法如共轭梯度法、牛顿法、最小二乘法等,具有计算量小、收敛速度快、结果稳定等优势。非线性方法在给定的参数搜索范围内对解进行搜索,对初始模型的要求较低,不依赖问题的梯度信息,具备较强的全局搜索能力,在频散曲线反演问题中具有重要的应用价值,因此近年来许多学者尝试将模拟退火法[5]、遗传算法[6-7]、粒子群算法[8-11]、差分进化算法[12]、蜂群算法[13]、蚱蜢算法[14]、蚁群算法[14]等多种非线性算法应用到频散曲线反演问题中。但尽管非线性算法在全局搜索方面具有一定的优势,由于频散曲线反演问题具有高维度、多局部极值的特征,因此使用非线性算法解决频散曲线反演问题时,仍不可避免地存在一定的概率陷入局部极值,一般需进行多次反演来得到可信的解,大大增加了非线性算法的计算量,给非线性算法的实际应用造成了一定的困难。因此如何优化非线性算法,在兼顾收敛速度的同时有效提高其全局搜索能力,进而增强解的稳定性和可靠性是一个有待进一步研究的问题。
麻雀搜索算法[15]作为一种新兴的非线性优化算法,具有收敛速度快、搜索能力强、稳定性好等特点,已在图像分割、路径规划等领域有了初步的研究和应用。本文将麻雀搜索算法引入频散曲线反演问题,同时针对频散曲线反演问题特征引入自适应t分布策略对算法进行改进,加强算法的全局搜索能力。理论模型数据实验表明,改进的麻雀搜索算法较好地克服了传统麻雀搜索算法易在迭代前期陷入局部最优解的缺陷,反演结果的准确性和稳定性得到显著提高,且具有较好的抗随机噪声干扰的能力,将改进的麻雀搜索算法与粒子群算法、差分进化算法等常见的非线性反演方法进行对比,结果表明改进的麻雀搜索算法在拥有较强的全局搜索能力的同时较好地兼顾了收敛速度,在多项性能评价指标上均取得了与粒子群算法和差分进化算法相比更好的结果。
1 原理方法
1.1 麻雀搜索算法
麻雀搜索算法是受麻雀觅食行为和反捕食行为启发而提出的一种新兴群体智能优化算法,假设在一个D维搜索空间中,存在N只麻雀,令第i只麻雀在D维搜索空间中的位置为xi=[xi1,xi2,…,xiD],其中i=1,2,…,N。麻雀搜索算法将N只麻雀分为发现者和加入者两类。其中发现者的适应度相对加入者较高,起着控制种群搜索的主要方向的作用,本文将种群中适应度位于前70%的麻雀划分为发现者。发现者的位置更新公式如下:
(1)
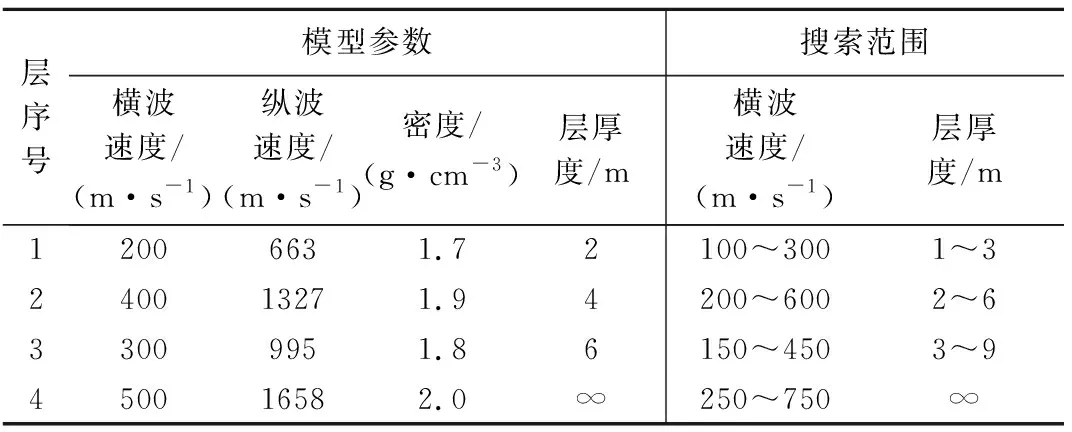
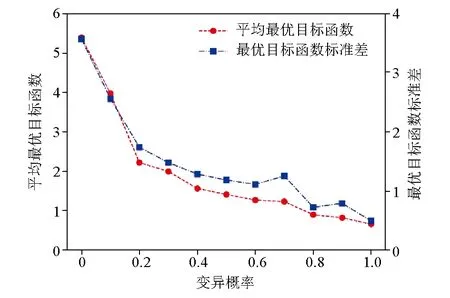
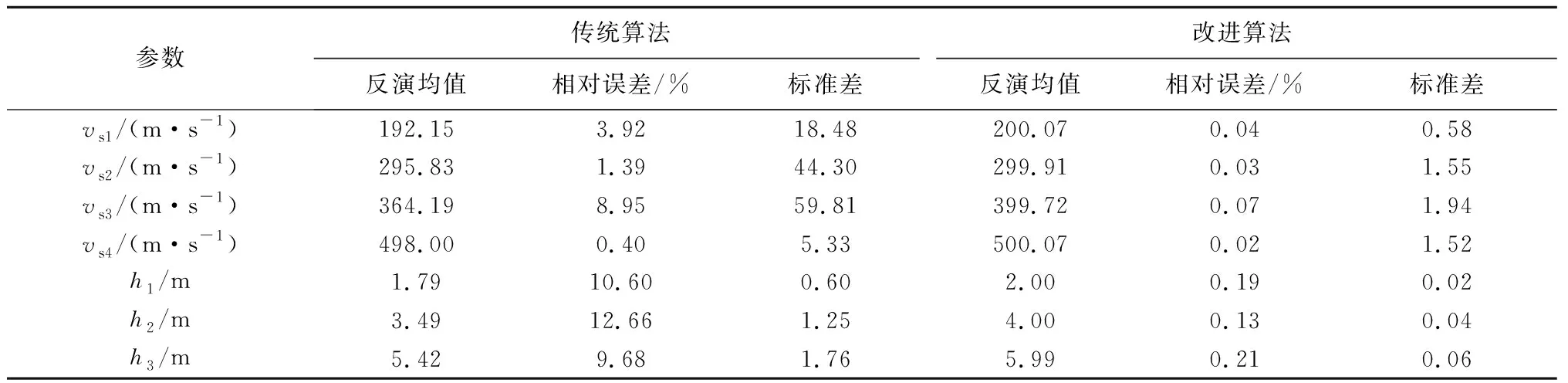
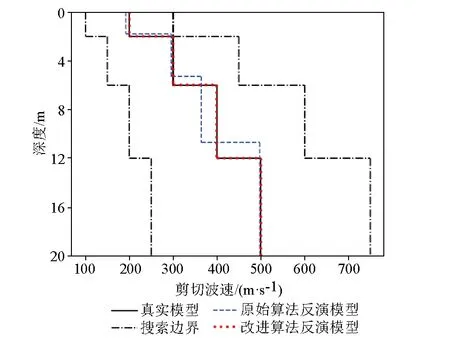
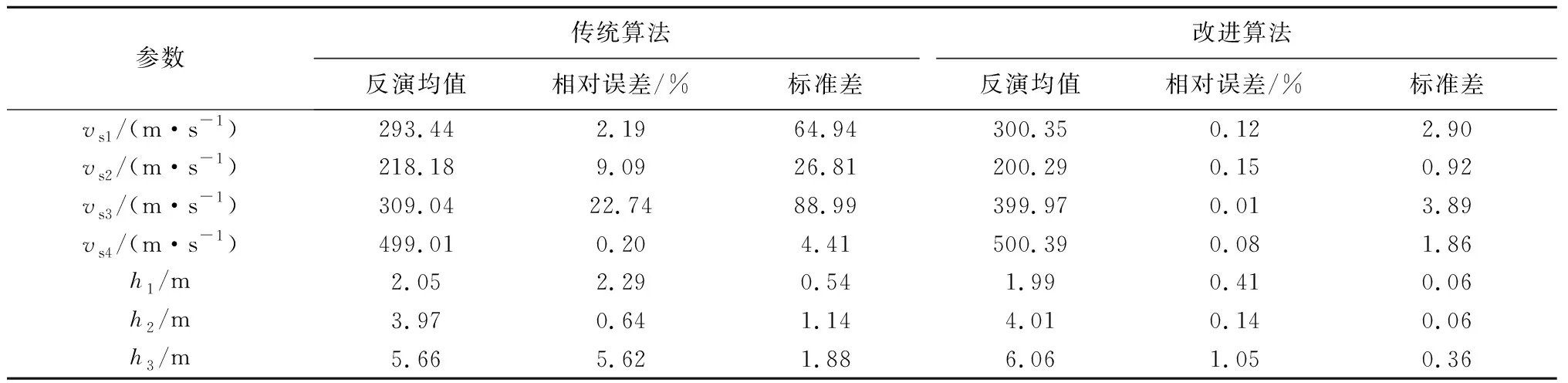
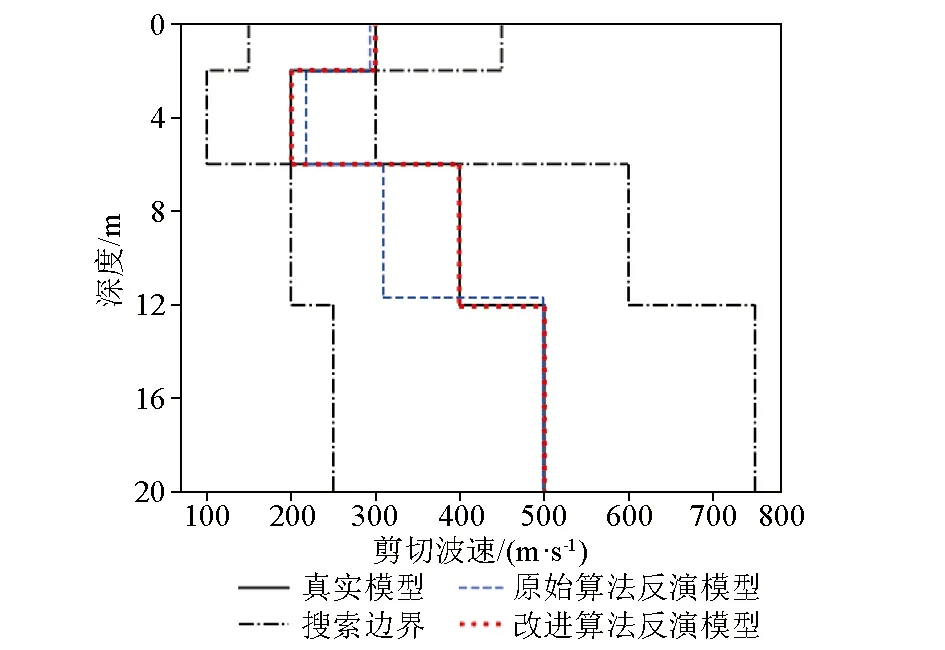
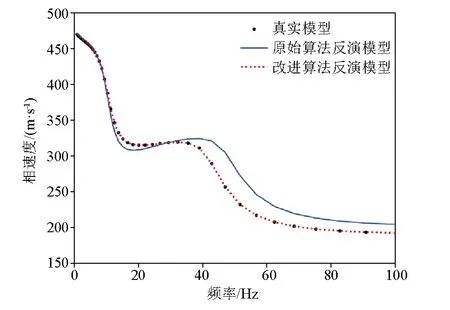
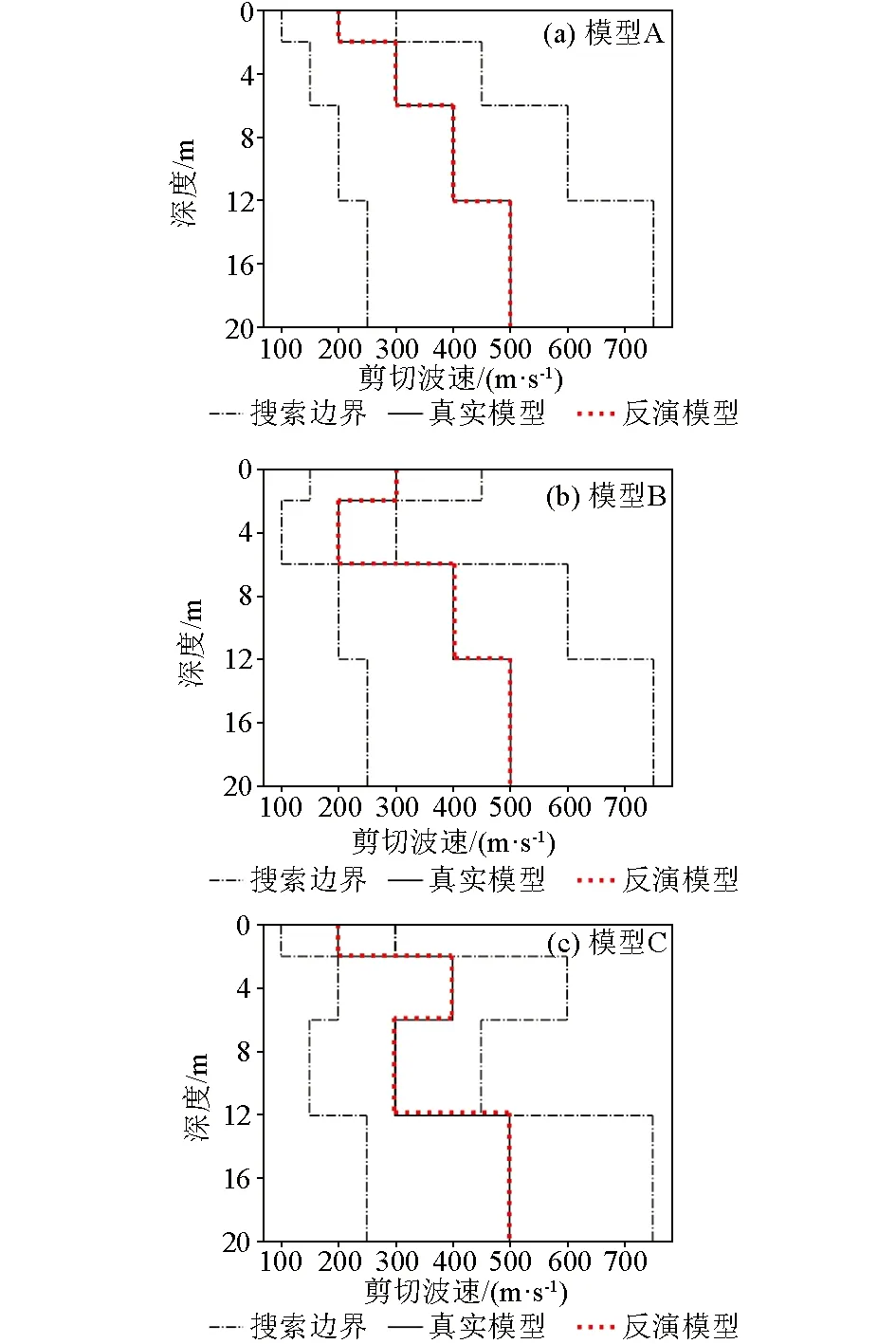
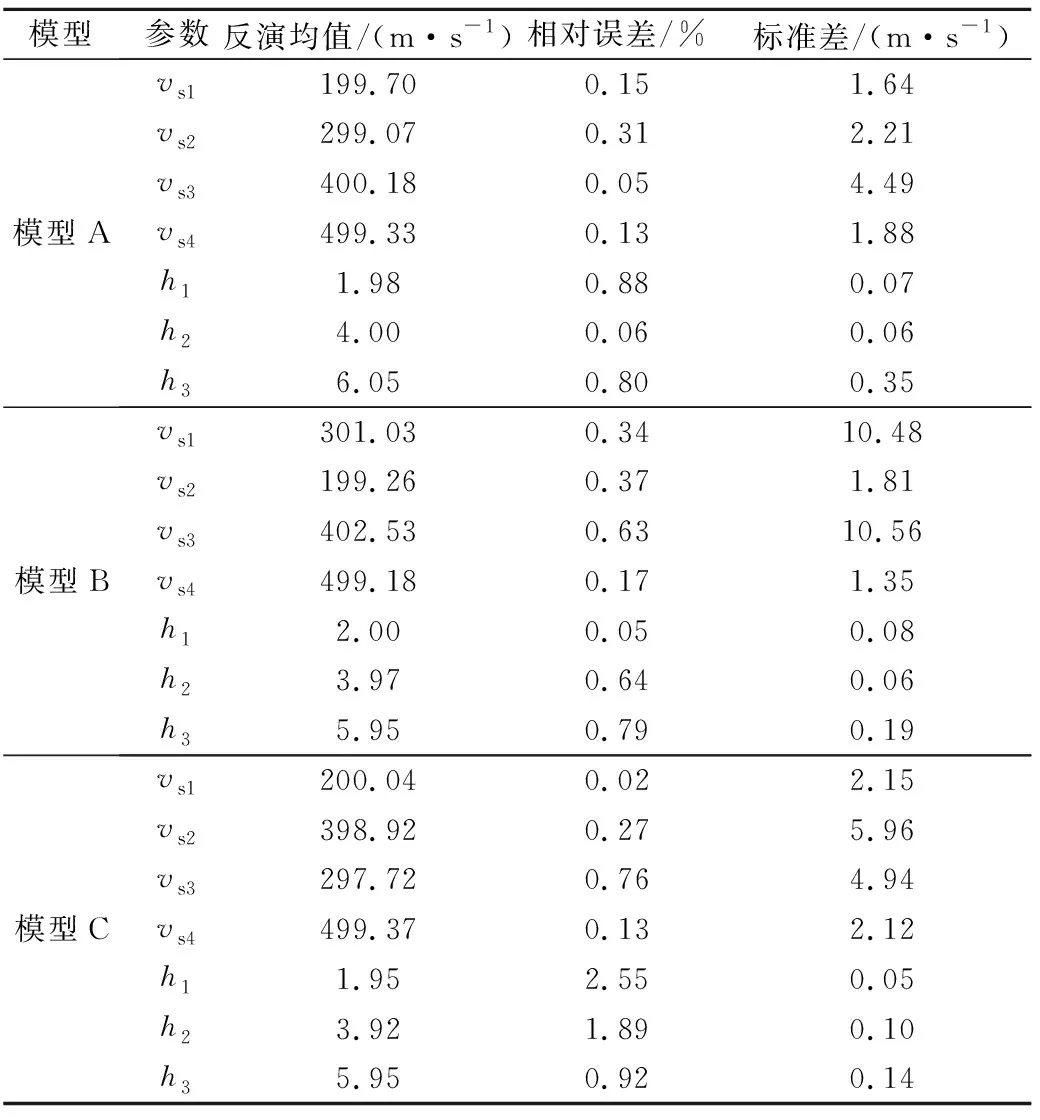
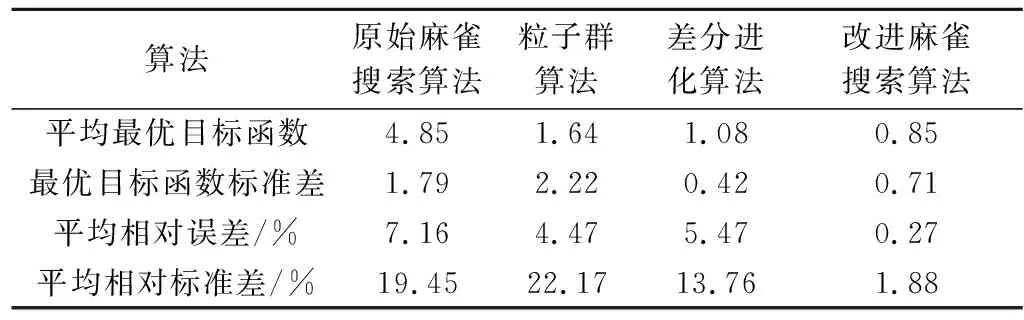
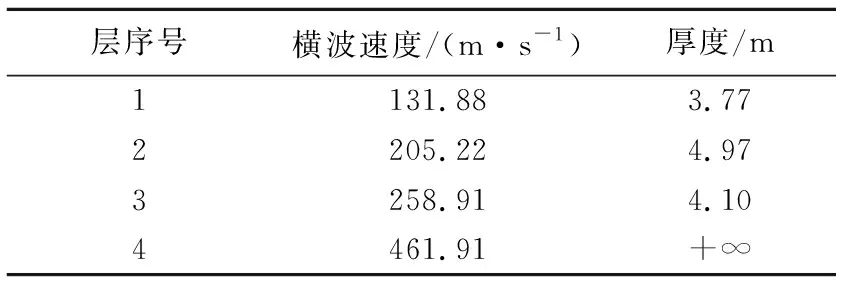
式中:t代表当前迭代次数;T表示最大迭代次数;α和R2为取值范围为(0,1]的均匀随机数;Q为服从标准正态分布的随机数;L表示大小为1×D、元素均为1的矩阵;ST表示预警值,取值范围为[0.5,1]。当R2 除发现者外,剩余的麻雀均划分为加入者,加入者的位置更新公式如下: (2) 无论属于发现者还是加入者,整个种群中的一部分麻雀也同时为警戒者。当危险靠近时,它们会放弃当前的食物移动到一个新的位置。本文在每次迭代时,随机选择种群中30%的个体为警戒者,其位置更新在发现者和加入者的位置更新之后进行,更新公式如下: (3) 式中:K为取值范围在[-1,1]之间的均匀随机数;ε是一个极小常数,用以避免fi=fworst时的除零错误;fi表示第i只麻雀的适应度值;fg和fw分别是当前的全局最优适应度和全局最差适应度。当fi>fg时,该麻雀将移动到全局最优位置附近;当fi=fg时,表明该麻雀已处于全局最优位置,将以一定步长在靠近或远离全局最差位置的方向上移动。 为提高传统麻雀搜索算法的全局搜索能力,避免早熟收敛,本文引入自适应t分布对算法进行改进。在发现者、加入者和警戒者的位置更新之后,以某一变异概率p对种群中的所有麻雀个体进行自适应t分布更新,更新公式如下: (4) (5) 为将改进麻雀搜索算法应用于频散曲线反演问题,定义目标函数如下式: (6) 式中:Vi表示真实模型频散曲线上第i个频散点的相速度;vi表示反演模型频散曲线上第i个频散点的相速度;N表示频散点总数。本文在1~100Hz范围内选取50个频散点来计算目标函数。此时频散曲线反演问题转换为目标函数的最小化问题,目标函数越小,表示反演模型频散曲线与真实模型频散曲线越接近。进行反演时,本文选取种群大小为35,同时考虑到相比于传统麻雀搜索算法,改进的麻雀搜索算法会在一次迭代中多次更新部分变异个体,为使两者的总计算量保持一致,本文令传统麻雀搜索算法的迭代次数为100次,改进的麻雀搜索算法的迭代次数为100/(1+p)次,其中p为变异概率。 为较全面地评估算法性能,本文建立了3种理论地质模型来模拟浅地表地球物理工作中的常见情形。3种理论模型的参数见表1~3。其中模型A 是一个速度递增的4层地质模型;模型B 是一个含有低速夹层的4层地质模型;模型C是一个含有高速夹层的4层地质模型。在水平分层介质中,瑞利波的频散特性主要受横波速度、纵波速度、密度、厚度的影响,其中横波速度和厚度对频散特性的影响较大。因此本文进行频散曲线反演时,将泊松比、密度视为已知参数,将横波速度和厚度视为待反演参数,纵波速度通过横波速度和泊松比的关系求得。考虑到实际工作中往往缺乏反演的地层参数的先验信息,本文设计各参数的搜索范围为真实值的0.5~1.5倍。 表1 四层速度递增模型参数和搜索范围(模型A)Table 1 Parameters and search range of four layer speed increasing model (model A) 表2 四层含低速夹层模型参数和搜索范围(模型B)Table 2 Parameters and search range of four layer model with low velocity interlayer(model B) 表3 四层含高速夹层模型参数和搜索范围(模型C)Table 3 Parameters and search range of four storey model with high-speed interlayer (model C) 自适应t分布改进策略通过以一定变异概率向个体施加变异扰动从而避免算法过早收敛于局部极值,提高算法的全局搜索能力,但当变异概率过高时,频繁施加的变异扰动可能会影响到算法的收敛速度。为确定变异概率的恰当取值,首先使用不同变异概率的改进麻雀搜索算法对模型A进行30次反演,图1展示了不同变异概率下取得的平均最优目标函数和最优目标函数标准差。可以看到随着变异概率的增大,平均最优目标函数和最优目标函数标准差始终保持总体下降趋势,当变异概率为1时,平均最优目标函数和最优目标函数标准差均取得了最小值。这说明自适应t分布改进策略通过在不同的搜索阶段自适应调整施加的变异扰动的大小,能够较好地避免频繁施加的扰动对算法收敛产生的不利影响,在提高算法全局搜索能力的同时也较好地兼顾了算法的局部搜索能力。本文之后所用的改进麻雀搜索算法的变异概率均为1。 图1 变异概率对改进算法反演性能的影响Fig.1 Effect of mutation probability on inversion performance of improved algorithm 为对改进前后的麻雀搜索算法在频散曲线反演问题上的性能进行对比,首先分别使用传统算法和改进算法对模型A进行30次反演,取30次反演的均值为最终得到的反演模型。图2、图3分别展示了反演模型和反演模型的频散曲线,表4统计了反演模型的相对误差和30次反演的标准差。可以看到改进算法和传统算法均比较好地拟合了真实模型频散点,其中改进算法的拟合效果相对更好。从各地层参数的反演精度上看,改进算法对各参数的反演值都与真实值十分接近,其中速度参数的相对误差均低于0.1%,厚度参数的相对误差均低于0.3%,而传统算法对各参数的误差均明显较大,特别是在第三层速度和第一、二、三层厚度上的相对误差都在10%左右;从各地层参数的反演稳定性上看,改进算法的优势同样显著,在速度参数上的标准差均低于2,厚度参数上的标准差均低于0.1,反映出使用改进算法进行多次反演获得的结果十分接近。 表4 模型A反演结果统计Table 4 Statistics of inversion results of model A 图2 模型A的原始算法与改进算法模型Fig.2 Original algorithm and improved algorithm model of model A 图3 模型A的原始算法与改进算法频散曲线Fig.3 Dispersion curve of original algorithm and improved algorithm of model A 为进一步评估反演算法在含低速夹层和含高速夹层等更复杂的地层环境下的性能表现,分别使用传统算法和改进算法对模型B和模型C进行30次反演,并取30次反演的均值为反演模型。图4、图5、图6和图7分别展示了反演所得模型及其频散曲线,表5和表6统计了改进算法与传统算法的相对误差和标准差。可以看到传统算法反演模型的频散曲线没有很好地拟合真实模型的频散点,反演得到的各参数特别是低速夹层和高速夹层的速度参数的相对误差也较大。与之相比,改进算法对模型B和模型C的频散点的拟合仍然十分理想,各参数的相对误差与模型A相比没有明显增大,准确反演得到了模型中低速夹层和高速夹层的相关参数,同时在反演稳定性方面也有着优异的表现,反映出改进算法对复杂的地层环境有着更好的适应性。 表5 模型B反演结果统计Table 5 Statistics of inversion results of model B 表6 模型C反演结果统计Table 6 Statistics of inversion results of model C 图4 模型B的反演模型Fig.4 Inversion model of model B 图5 模型B的反演模型频散曲线Fig.5 Dispersion curve of inversion model of model B 图6 模型C的反演模型Fig.6 Inversion model of model C 图7 模型C的反演模型频散曲线Fig.7 Dispersion curve of inversion model of model C 与理论频散曲线不同,实际频散曲线往往包含一定程度的随机噪声,可能会对算法的反演性能造成影响。为对此进行研究,向上述3种理论模型的频散曲线中分别添加10%的高斯白噪声,再使用改进算法对加噪频散曲线进行30次反演,并取其平均值作为最终的反演模型。图8展示了用于反演的加噪频散点和在无噪、加噪条件下得到的反演模型的频散曲线,图9展示了加噪频散曲线的反演结果。 图8 含噪频散曲线的反演模型Fig.8 Inversion model with noise 图9 有无噪声条件下地质模型的频散曲线Fig.9 Inversion results of geological model with or without noise 可以看到算法较好地克服了频散曲线中的随机噪声干扰,在加噪条件下反演得到的反演模型及其频散曲线均与无噪条件下的反演结果相近。表7展示了在加噪条件下对3种地质模型进行反演的相对误差和标准差,与无噪条件下的反演结果相比,加噪条件下反演的相对误差和标准差有较小程度的增大,从其绝对水平来看各地层的反演参数与真实值仍然是十分接近的,反映出改进算法对频散曲线中的随机噪声不敏感,能够较好地应用于含噪频散曲线的反演问题。 表7 加噪条件下3种地质模型的反演结果统计Table 7 Statistics of inversion results of three geological models under noise conditions 为进一步验证本文所述的改进麻雀搜索算法在频散曲线反演问题中的性能优势,将其与粒子群算法和差分进化算法这两种较为常见的非线性反演算法进行对比。两种算法的种群大小和迭代次数均为35和100。对于粒子群算法,令其惯性权重为0.6,全局学习因子为1.8,个体学习因子为2.2;对于差分进化算法,采用DE/rand/1/bin差分策略,令其缩放因子为0.5,交叉概率为0.7。使用每种算法进行30次反演,并将反演的平均值作为最终的反演模型。图10展示了原始麻雀搜索算法、粒子群算法、差分进化算法和改进麻雀搜索算法的30次迭代的最优目标函数曲线和平均最优目标函数曲线。首先可以看到原始麻雀搜索算法在迭代前期极易陷入局部最优解,反演得到的最优目标函数相比于其他3种算法明显偏大;粒子群算法在迭代前期的收敛速度最快,但迭代的中后期,部分次数的反演始终无法跳出局部最优,影响了算法的平均表现;差分进化算法在全局搜索方面的性能表现较好,从其最优目标函数曲线可以看到多次反演的收敛速度十分稳定,不易陷入局部最优,但同时注意到在迭代后期,差分进化算法的收敛仍不充分,最优目标函数集中在1附近,不容易取得最优目标函数更小的反演结果,反映出差分进化算法的局部搜索能力较弱,可能会对反演所得的地层参数的精度造成影响;改进麻雀搜索算法较好地克服了原始麻雀搜索算法在迭代前期易陷入局部最优的缺陷,同时在迭代中后期也具有较好的局部搜索能力,得到了一定数量的收敛较充分的反演结果,反映出改进的麻雀搜索算法较好地兼顾了算法的全局搜索和局部搜索性能。 a—原始麻雀搜索算法;b—粒子群算法;c—差分进化算法;d—改进的麻雀搜索算法a—original sparrow search algorithm;b—particle swarm optimization;c—differential evolution algorithm;d—improved sparrow search algorithm图10 30次反演的最优目标函数曲线和平均最目标函数曲线Fig.10 Optimal objective function curve and average optimal objective function curve of 30 inversions 表8展示了上述4种算法进行30次反演的平均最优目标函数、最优目标函数标准差、平均相对误差和平均相对标准差。其中前、后两个指标分别从频散曲线拟合和地层参数反演两个角度对算法的准确度和稳定性进行衡量,可以看到差分进化算法的最优目标函数标准差取得了明显优于其他算法的最小值,而其平均最优目标函数也与改进的麻雀搜索算法接近,但其平均相对误差和平均相对标准差却明显差于改进的麻雀搜索算法,这说明由于频散曲线反演问题的多解性特征,频散曲线拟合的好坏并不能完全反映地层参数的反演情况,而由于差分进化算法的收敛较不充分,其受多解性的影响也更大,最终导致了差分进化算法在频散曲线拟合和地层参数反演两方面的性能差异。 表8 不同算法的反演性能统计Table 8 Inversion performance statistics of different algorithms 为进一步验证改进的麻雀搜索算法的有效性,将其应用于三峡新能源庆云储能电站示范项目实测数据,工区拟建于山东省德州市。拟建场地地形较平坦,其岩性主要由粉土、粉质黏土、黏土、粉细砂构成,细分为素填土1、粉土2、粉质黏土3、黏土4、粉细砂5,其中K41钻孔(孔口高程38.53 m)的地层描述如表9所示。可见工区地层的分层情况较为复杂,本文进行反演时将其简化为4层模型,假定泊松比和密度已知,反演横波速度和厚度,各地层参数的取值及搜索范围如表10所示。 表9 工区K41钻孔地层描述Table 9 Description of the K41 drill of work area 表10 模型参数及搜索范围Table 10 Parameters and search range of model 使用改进的麻雀搜索算法对实测数据频散曲线进行30次反演,取30次反演的均值为最终得到的反演模型。表11展示了反演模型的各地层参数,图11对比了实测频散曲线和反演模型频散曲线。可见反演模型频散曲线较好拟合了实测频散曲线。将反演模型与钻孔数据进行比对,可见反演模型与钻孔所反映的地质分层情况能够较好对应,其中反演模型的第1、2、3和4层分别对应于表9所示1~2、3、4和5层,但同时也应注意到,实测数据所对应的实际地层分层情况较为复杂,岩性分层与波阻抗分层也并不完全一致,使得反演模型的地层厚度和钻孔所示的地层厚度存在一定的差异,有待于今后的进一步研究。 表11 实测数据反演结果统计Table 11 Statistics of inversion results of measured data 图11 实测数据反演频散曲线Fig.11 Inversion results of measured data 本文将改进的麻雀搜索算法应用于瑞利波频散曲线反演,与粒子群算法等常见的非线性算法相比,得出了以下结论: 1) 相较于传统麻雀搜索算法,改进的麻雀搜索算法的全局搜索能力显著增强,在频散曲线反演问题中具有更好的求解精度和稳定性。 2) 改进的麻雀搜索算法具有较好的抗噪能力。采用改进的麻雀搜索算法对加噪频散曲线进行反演,在反演精度、反演稳定性上改进的麻雀搜索算法仍然拥有较好的性能表现。 3) 改进的麻雀搜索算法在拥有较强的全局搜索能力的同时很好地兼顾了收敛速度,取得了与粒子群算法和差分进化算法相比更好的效果。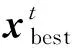
1.2 自适应t分布改进策略
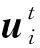
1.3 改进麻雀搜索算法在频散曲线反演问题中的应用


2 理论模型反演
2.1 无噪理论模型频散曲线反演




2.2 含噪理论模型频散曲线反演

3 与其他非线性算法的性能比较

4 工程验证



5 结论
