基于分段采样和MCA的地震数据重建

王德英,张凯,李振春,张医奎,许鑫

(1.中国石油勘探开发研究院西北分院，甘肃 兰州 730030；2. 中国石油大学(华东) 地球科学与技术学院，山东 青岛 266580；3. 物华能源科技有限公司，陕西 西安 710067)

0 引言

在实际地震勘探中，数据体内容复杂且容量巨大，加之野外地形条件和经济成本的限制，地震勘探数据在空间方向上经常进行不规则采样。在陆地上这种情况可能起因于地震道的布置受到建筑、湖泊、禁采区等复杂地形限制，另外人工放炮的不充分激发也可能起因于坏道或者严重污染道的出现，从而导致采集到的地震数据不规则、不完整或出现空间假频。在海上地震勘探中，则可能由于电缆的水平偏移等引起，这种稀疏分布的地震数据难以满足高分辨地震勘探的需要[1]。

压缩感知数据恢复的3个关键因素分别是：对待恢复数据的稀疏表示、对完整数据的随机采样和最优化差值重建算法。其中基于压缩感知的数据采样通常是完全随机采样，这种采样方式会导致采样点间隔过于稀疏或密集，当采样点过于稀疏时会导致重要信息丢失，影响恢复效果；采样点过于密集则造成多余采样，违背压缩感知节约经济成本的原则。唐刚[2]引入泊松碟采样方式，提高了重建效果，但该采样方式由于事先固定采样，也不能根据野外地质条件灵活调整，使其在实际应用中有一定局限。Leneman提出了Jitter采样方式[3]，首先应用于图像处理。Hennenfent G等[4]指出在利用非线性稀疏性促进求解方法时，随机采样相比等间距的规则采样可以获得更好的数据重建效果。Hennefent G等[4]、唐刚[2]将其引入到地震数据重建中，使采样点分布相对均匀，在一定程度上能够根据地质条件灵活调整。Herrmann F J等[5]使用Jitter采样进行了基于压缩感知的地震数据重建。Mosher C C[6]提出了NUOS采样方案并用于在感知成像技术(compressed sensing imaging,CSI)中寻找炮点和接收点的最佳位置。Yang等[7]在2015年完成CSI技术在陆地、海洋和OBN勘探中的生产和应用，提出了一种分段随机采样方法，并对其进行了理论分析。以上研究结果表明，与随机采样和Jitter采样相比，相同次数下分段随机采样的重建效果优于其他两种方法。

压缩感知理论的一个重要前提是信号的稀疏性。由于地震数据通常不是稀疏的，因此如何找到合适的稀疏字典，使得信号在该字典下的系数是稀疏的，即能对信号进行稀疏表示，就显得尤为重要。现今已有多种数学变换被用于地震数据重建，如Fourier变换[8]、Curvelet变换[5]、Wavelet变换[9]、Dreamlet变换[6]、Shearlet变换[10]等。由于地震数据通常由不同类型的元素组成，单一变换往往不能充分、有效地将其全部表达，李海山等[11]提出形态分量分析(morphological component analysis，MCA)方法。该方法主要利用不同信号之间成分的差异对信号进行分离，最早由Starck等提出并将其应用于图像的去噪与修复，且取得良好效果，目前被广泛应用于信号的去噪、重建、分隔、修复以及融合等多种领域。李海山等[11]将MCA方法引入地震数据重建领域，取得了较好效果。周亚同等[12]在MCA框架下定量评价了多种不同稀疏字典组合的数据重建效果，判定离散余弦变换(discrete cosine transform,DCT)与Curvelet字典组合具有最高的重建精度。刘成明等[10]和张良等[13]指出Shearlet变换作为一种新型的多尺度几何变换，具有比Curvelet变换更好的方向性以及其自身所具有的各向异性特点，从而拥有更突出的稀疏表达能力，认为基于Shearlet变换的重建算法可望取得精度更高的重建结果。

受上述研究的启发，将Shearlet变换应用到MCA中，它能准确地描述数据的局部特征，因此，有必要寻求一种全局型变换来与之配合。经过反复测试，确定Shearlet+DCT的重建效果优于单一数学变换和其他字典组合。此外，我们还比较了不同采样方法的重建结果，证明了SRS(segmented random sampling)更有利于CS的重建。本文采用SRS和Shearlet+DCT对实际资料进行处理，均取得理想结果。

1 基本理论

1.1 压缩感知理论

缺失地震数据的恢复可以看作一个压缩感知问题，一个不满足奈奎斯特采样定理的信号可以通过某些稀疏变换在特定的稀疏域来恢复。地震数据的重建问题可以描述为由一组不完整数据通过线性算子的作用恢复出完整的数据，假设线性正演模型：

y=Rx+e,

(1)

其中：y代表采集的地震数据；x表示待恢复的数据；R表示随机采样矩阵；e代表随机噪声。

压缩感知技术的第一条件是信号可以在某一稀疏域被稀疏表示，假设数据x′是数据x在稀疏域F的稀疏表示，则方程(1)可以改写为：

y=Ax′+eA=RFH,

(2)

其中，FH是稀疏变换F的共轭转置矩阵，如果x′中有k个非零元素且k≪L，我们视x′是稀疏的，它可以通过凸优化问题来恢复[12]。

(3)

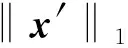
y′=FT〈x〉 。

(4)

1.2 基于形态分量分析的地震数据重建

MCA方法认为，信号是由形态不同的多个分量线性组合而成，每个分量都能找到一个字典，该字典只能稀疏表示对应的形态分量，而无法稀疏表示其他分量。

给定二维信号X，假设它由K个不同形态的分量线性组合而成，即

(5)

式中：Xk为K个形态分量，它可被字典Dk稀疏表示；ak为对应的稀疏系数。

地震数据的重建可表示为：

Y=RX，

(6)

式中：X表示理想的完整地震数据；Y表示实际采集的含缺失道地震数据；R表示采样矩阵。

在MCA框架下，式(6)可被表示为：

(7)

将式(7)改写为无约束最优化问题，求解得：

(8)

式中：λ为拉格朗日乘子，用来平衡l1范数项和l2范数项所占比重。

1.3 MCA求解方法

对于恢复算法的求解，Sardy等[9]结合块坐标松弛(Block coordinate relaxation，BCR)算法给出如下基于形态分量的求解方法。

输入：采样矩阵R，字典组合D=[D1,…,DK]，缺失地震数据Y，总迭代次数N

输出：重建地震数据X

1) for:n=1:N；

2) 残差r(n)=Y-R·sum(X1,…,XK)

3) for:k=1∶K

6) 应用阈值模型减小λ

7) end

8) end

9)X=sum(X1,…,XK)

其中：D-1表示字典D对应的逆变换；Tλ为阈值函数，其公式为：

(9)

除了阈值λ外，我们还有另一个独立参数p可以灵活选择，以获得更好的性能。在泰勒级数的基础上，指数阈值可被认为是一个光滑的0范数约束。当|x|≫λ时，它是p阈值算子的近似，可简化为p=0时的Stein阈值算子和p=1时的软阈值。在求解算法时，需要调整拉格朗日乘子来得到最优解。步骤如下:首先选取较大的变换域系数作为阈值，得到稀疏近似解。其次，不断减小该值以包含更多的变换域系数，并通过连续迭代逼近最优解。阈值选择策略称为阈值模型，它影响算法的速度和精度。标准阈值模型包括线性模型、指数模型和数据驱动模型。本文采用指数模型，其形式为：

(10)

式中：λmax、λmin分别为所选最大、最小正则化参数；qmax和qmin是用户定义的百分比；N是迭代次数。

1.4 稀疏字典的选取

稀疏字典的选取是MCA方法的核心问题，不同的字典对稀疏表示的效果影响很大。周亚同等[12]已对Curvelet字典的不同组合方案进行了实验，最终认定离散余弦变换(DCT)与Curvelet字典组合具有最高重建精度。Curvelet具有刻画多尺度、多方向各向异性的能力，能够很好地表达地震信号中的曲线状边缘特征；但与Shearlet变换相比，其稀疏表示能力相对弱一些。Shearlet变换的数学结构较简单，它通过对一个函数进行伸缩、平移、旋转来生成基函数，该特点与小波类似，却正是Curvelet变换所欠缺的，所以Shearlet字典非常适用于图像恢复重建。DCT变换是一种在信号和图像处理中常用的数学变换，它具有一个很重要的特性——能量集中，即经DCT变换后信号能量非常集中，且大多数系数都集中在低频部分。经过多次的对比实验得出利用MCA框架下Shearlet和DCT字典组合的方法进行数据重建的效果最好。

2 采样方法

压缩感知的关键技术之一是随机欠采样方法，因为它可以把混淆真实频率的相干噪声转化成容易滤除的不相干噪声，即使这些随机噪声和真实频谱相互叠合在一起，仍然可以通过迭代的方式检测出真实频率。因此，相干噪声的程度很自然地就成为衡量一种欠采样方法效果的重要标准之一。然而单纯的随机采样会造成采样点过于聚集或者过于分散的情况，难以达到理想的重建效果，同时也不能根据野外实际地质条件灵活调整，因此引入Jitter欠采样方式，以控制采样间隔，更加适合地震数据重建。Jitter采样方法首先将待处理区域划分成若干个子区域，然后在每个子区域内都随机地强制采一个点。由于每个子区域都有采样点，相邻缺失地震道之间的间隔也就得到了控制，同时也保持采样点的随机性，可将假频转化成低幅度噪声，使真实频率更容易检测[14-23]。但是Jitter欠采样过程中会存在剩余采样点，不容易使Jitter参数与离散随机变量相等，导致无法达到最优Jitter采样。分段随机采样在保证采样点的规则性与随机性的同时，很好地克服了这一缺点。

分段随机采样的设计主要分为两个步骤：第一步是根据项目要求及工区实际地质条件，设计一个充分完整规则的观测系统。压缩感知的作用与目的就是尽可能地减少炮点和检波点的数量，不仅可以节约成本也可以扩大地震勘探区域或提高空间分辨率[21,24-26]。第二步则是对第一步生成的完整观测系统进行优化。非规则观测系统设计步骤如下：

1)根据地震勘探项目与客观条件确定欠采样缺失因子P。

2)假设一条有N个检波器的接收道可以表示为：

X=[x(1),x(2),…,x(N)] 。

(11)

3)给定一个分段长度L，X被分成若干个长度为L的Si，在Si内根据欠采样缺失因子P确定采样点数量，则实际的接收点可以表示为：

Xr=x(h(m)),X0=0 ，

(12)

其中，h(m)代表随机采集m个点，0代表未采集的点。

4)炮点的不规则化方法与采样点相同。

5)将不规则的炮点和检波点输出到SPS文件中。

图1是分段随机采样的示意，表现了规则采样点不规则化的过程。从图中可以看出几个采样点共同位于一个小段(P=50%)中，黑色代表采样点，白色代表未被采样的点。每一小段的长度L=4，欠采样缺失因子。沿着这条检波道，每4个点被分成一段，段中50%的点被随机选择。每小段的采样点个数为L×P=2，此检波道的最大采样间隔为4。在选择分段长度L时也要考虑欠采样缺失因子的大小，尽量使L×P的结果是整数[5]，最大采样间隔也是由这2个参数来决定。如果L=4，P=25%,则采样间隔是6。从图2f、g、h可以看出，最后3种采样方法所采集的缺失数据没有假频，频谱中只存在部分噪声。相比之下，分段随机采样所产生的噪声最小。从时间域图像分析，分段随机采样能更好地保留有效信息。

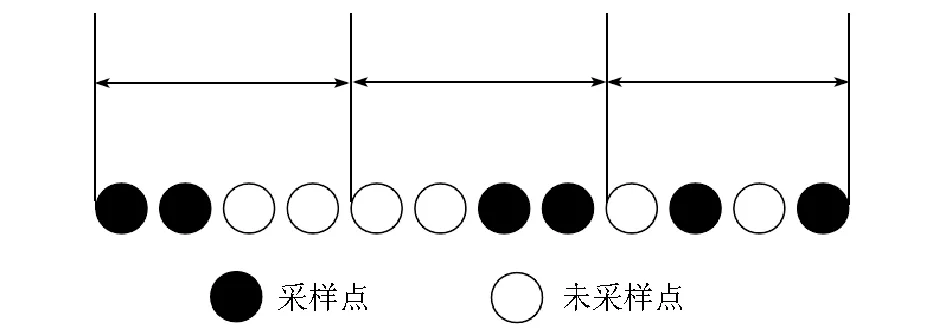
图1 分段随机采样示意Fig.1 Schematic diagram of segmented random sampling

a—合成地震记录;b—合成地震记录频谱;c—规则欠采样数据;d—规则欠采样数据频谱;e—完全随机采样数据;f—完全随机采样数据频谱;g—分段随机采样数据;h—分段随机采样数据频谱a—synthetic seismic record;b—spectrum of synthetic seismic record wavenumber;c—synthetic seismic data after regular sampling;d—spectrum of synthetic seismic data after regular sampling wavenumber;e—synthetic seismic data after random sampling;f—spectrum of synthetic seismic data after random sampling wavenumber;g—synthesized seismic record after SRS;h—spectrum of synthesized seismic record after SRS图2 欠采样数据及其频谱Fig.2 Sampled data and spectrum

3 数值实验

3.1 评价参数

为了对重建结果进行定量描述，本文引入两个评价参数，其定义如下：

1)信噪比RS/N

(13)

其中，X表示完整地震数据；X′表示重建地震数据。

(14)

其中，MSE表示均方差，其计算公式如下：

(15)

3.2 实际数据模型试算

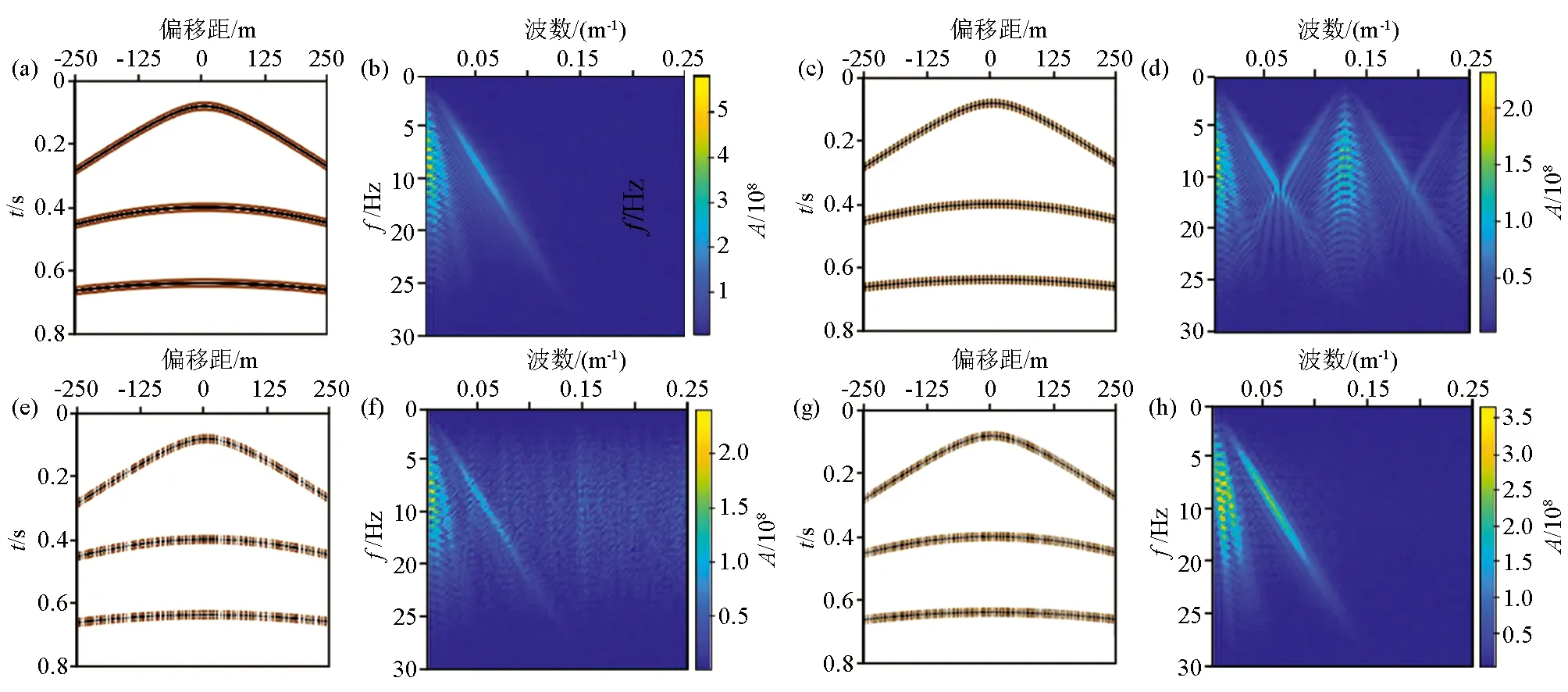
为了充分说明分段随机采样与MCA重建技术的优越性，选用3种随机采样方法(完全随机采样、Jitter采样和分段随机采样)对原始数据进行采样，得到3种缺失数据，比较它们单一DCT字典、单一Shearlet字典和MCA框架下Shearlet和DCT字典组合的重建效果。本文选择了某地区真实的炮记录进行实验(为便于观察重建质量，数据已经过去噪处理)，其时间采样频率为1 ms，含有200道，每道有600个采样点。图3b、c、d分别是与数据大小相等的随机采样矩阵、Jitter采样矩阵和分段随机采样矩阵，采样点的缺失率均为50%；图3e、f、g分别是图3a经过3种采样矩阵作用得到的3种缺失数据，可以看出图3e中存在多连续道缺失，过多的连续数据缺失是影响重建效果的主要原因。相反，图3f、g保留了缺失道的随机性也控制了采样点的最大间隔，对比图3c、d可以看出分段随机采样的这种控制能力更强。

a—原始数据;b—随机采样矩阵;c—Jitter采样矩阵;d—分段随机采样矩阵;e—完全随机采样数据;f—Jitter采样数据;g—分段随机采样数据a—original data;b—Random sampling matrix;c—Jitter sampling matrix;d—segmented random sampling matrix;e—missing data after random sampling;f—missing data after Jitter sampling;g—missing data after segmented random sampling图3 原始数据、采样矩阵和缺失数据Fig.3 Original data, sampling matrix and missing data

此实验在使用单一稀疏域进行重建时选用DCT字典和Shearlet字典，它们分别通过DCT变换和Shearlet变换生成，求解算法为FPOCS算法，其迭代次数均是120次。图4是利用单一DCT字典的重建结果和所对应的差值剖面。差值剖面通过重建数据与原始数据作差来得到，在没有造影参与的情况下可用来表示重建误差。从图中可以看出在单一DCT稀疏域中，无论随机采样、Jitter采样和分段随机采样都获得不理想的重建效果。这是因为DCT字典的特征是能量集中且大多数系数都集中在低频，使其在重建较为复杂的实际资料时具有一定的局限性。对比图4a、b、c可以明显的看出，图4c的同相轴最为光滑、连续，对比图4d、e、f也可以看出分段随机采样的重建误差的浮值(分段随机采样重建误差绝对值0.03；Jitter采样重建误差绝对值0.04；随机采样重建误差绝对值0.06)低于前两者，这也说明了分段随机采样的优越性。

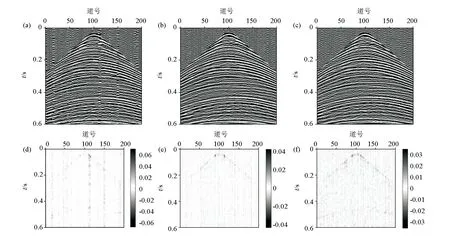
a—随机采样的DCT重建结果;b—Jitter采样的DCT重建结果;c—分段随机采样的DCT重建结果;d—随机采样的DCT差值剖面;e—Jitter采样的DCT差值剖面;f—分段随机采样的DCT差值剖面a—DCT reconstruction result of random sampling;b—DCT reconstruction result of Jitter sampling;c—DCT reconstruction result of segmented random sampling;d—DCT reconstruction result of segmented random sampling;e—DCT difference profile of Jitter sampling;f—DCT difference profile of segmented random sampling图4 DCT字典重建数据与差值剖面Fig.4 Reconstruction results and difference profiles of DCT dictionary

对比图4和图5可以发现单一Shearlet字典总体重建效果远好于单一DCT字典。这是因为Shearlet变换是基于具有合成膨胀的仿射系统构建的新型多尺度几何变换，用于对图像等高维数据进行更为稀疏的表示。相比于DCT变换以及其他稀疏变换，Shearlet变换具有更简单的数学结构及更突出的稀疏表示能力。现阶段，综合时间成本与重建效果的双重因素，在恢复实际资料时Shearlet变换是非常实用的选择。从图5可以看出无论哪一种采样方法，Shearlet变换都可以取得良好效果，但观察图5d会发现由于完全随机采样的缺点，在连续多道缺失的地方仍然会存在部分误差，相比之下Jitter采样和分段随机采样可以很好地解决这一问题。

a—随机采样的Shearlet重建结果;b—Jitter采样的Shearlet重建结果;c—分段随机采样的Shearlet重建结果;d—随机采样的Shearlet差值剖面;e—Jitter采样的Shearlet差值剖面;f—分段随机采样的Shearlet差值剖面a—Shearlet reconstruction result of random sampling;b—Shearlet reconstruction result of Jitter sampling;c—Shearlet reconstruction result of segmented random sampling;d—Shearlet reconstruction result of segmented random sampling;e—Shearlet difference profile of Jitter sampling;f—Shearlet difference profile of segmented random sampling图5 Shearlet字典重建数据与差值剖面Fig.5 Reconstruction results and differences profile of Shearlet dictionary

图6展示了Shearlet与DCT字典组合的重建数据，可以看出重建效果优于单一Shearlet字典和单一DCT字典。虽然误差最大绝对值略高于单一DCT字典误差最小绝对值(Shearlet+DCT重建误差绝对值0.04；DCT重建误差绝对值0.03；Shearlet重建误差绝对值0.06)，但误差集中于直达波区域，对后期处理无过大影响，而字典组合的中深层误差基本为0。对比3种字典的重建结果也可看出图6所示结果的图像更为干净，同相轴更为连续清晰。对比图6e、f可知，字典组合对重建Jitter采样数据和分段随机采样数据的效果都很理想，但在对数据边界处理的方面来看，分段随机采样仍具有一定优势，两者差别见图中红圈部分。

a—随机采样的Shearlet+DCT重建结果;b—Jitter采样的Shearlet+DCT重建结果;c—分段随机采样的Shearlet+DCT重建结果;d—随机采样的Shearlet+DCT差值剖面;e—Jitter采样的Shearlet+DCT差值剖面;f—分段随机采样的Shearlet+DCT差值剖面a—Shearlet+DCT reconstruction result of random sampling;b—Shearlet+DCT reconstruction result of Jitter sampling;c—Shearlet+DCT reconstruction result of segmented random sampling;d—Shearlet+DCT reconstruction result of segmented random sampling;e—Shearlet+DCT difference profile of Jitter sampling;f—Shearlet+DCT difference profile of segmented random sampling图6 字典组合重建结果及差值剖面Fig.6 Reconstruction results and difference profiles of Dictionary Combination

基于压缩感知的数据重建不只是一个找回丢失数据的过程，同样也是一个提高信噪比的过程。表1展示了3种采样数据在使用不同稀疏字典重建前后的信噪比和峰值信噪比，两者的计算方法在3.1节给出。从表中可以看出本文提出方法(分段随机采样与Shearlet+DCT组合)的重建结果无论信噪比和峰值信噪比均有最大的提升。

表1 重建结果评价参数Table 1 Evaluation parameters of reconstruction results

不同的拉格朗日乘子数值对恢复重建的效果不同。从图7中可以看出选取拉格朗日乘子为0.95时，重建后信噪比较0.90时具有更高值，图7a、b的迭代次数分别是100和200。迭代次数越多，重建结果信噪比越高，但也要承担相应的时间成本。在本文的实验中，迭代次数选120次时，已经能够达到很好的重建效果。

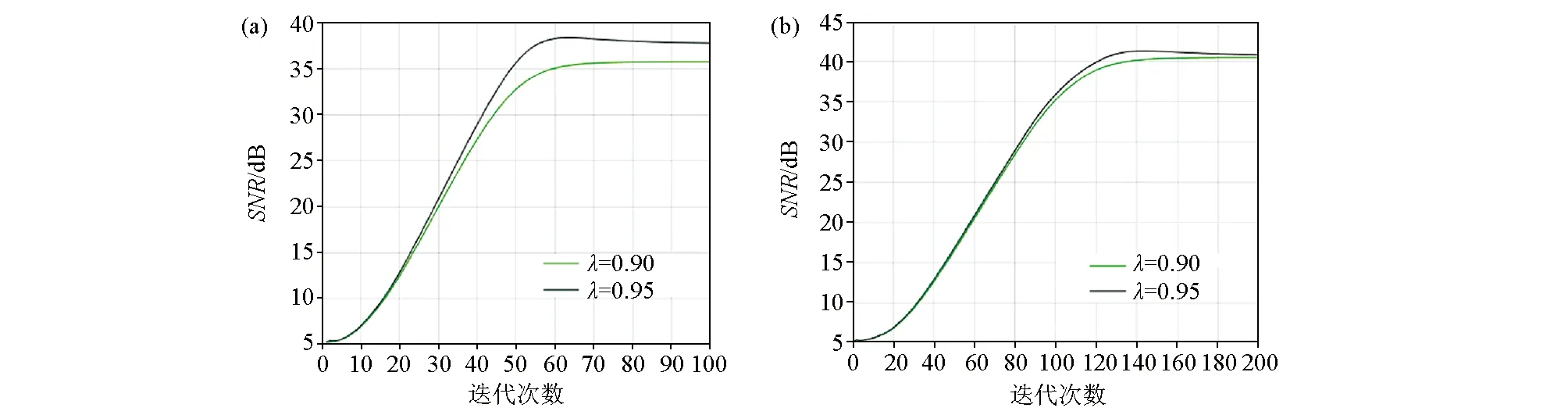
图7 拉格朗日乘子及迭代次数与重建信噪比Fig.7 Lagrangian multiplier and number of iterations and reconstruction signal-to-noise ratio

3.3 含噪模型试算

为更深地探究地震数据重建对信噪比的影响，对含噪合成地震数据进行欠采样及重建实验。为突出所提方法的优势，选择DCT、Shearlet、Shearlet+DCT进行实验，并对比3种方法的重建效果及定量评价值。含噪合成地震记录共500道，每道含800个时间采样点。图8为数据的分段随机采集过程，图8a、b分别展示了原始数据及分段随机欠采样数据。图9展示了3种重建方法的重建结果，从图中可以看出本文所提方法(Shearlet+DCT字典)的重建数据具有更少的噪声干扰。从表2中可以看出本文所提方法对原始数据的信噪比具有明显提升作用，且提升量高于单一DCT字典与单一Shearlet字典。

a—原始含噪数据;b—分段随机采样50%数据a—original noise data;b—50% missing data图8 含噪合成地震数据欠采样Fig.8 Under sampling of noise synthetic seismic data

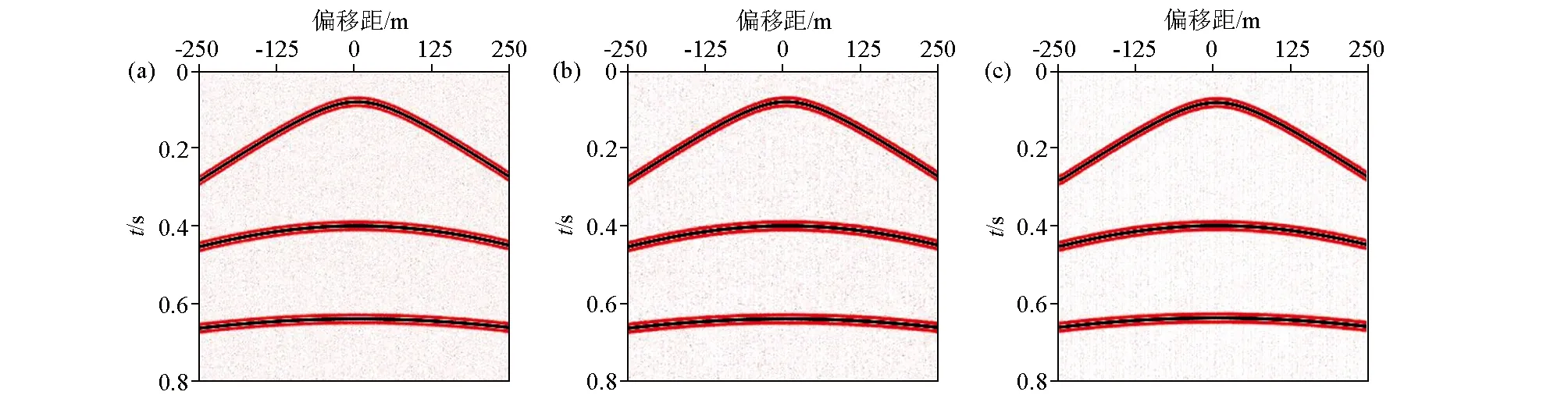
a—DCT重建结果;b—Shearlet重建结果;c—Shearlet+DCT重建结果a—DCT reconstruction result;b—Shearlet reconstruction result;c—Shearlet+DCT reconstruction result图9 三种重建结果Fig.9 Three reconstruction results

表2 重建结果评价参数Table 2 Evaluation parameters of reconstruction results

3.4 连续缺失模型试算

以上采样方法基于压缩感知技术，压缩感知的理论基础是随机采样方式。但在实际生产中，由于实际工区地形限制，经常会出现地震道连续缺失的情况，难以满足随机采样的假设，因此我们添加复杂实际地震图像连续缺失重建实验。本节不设置对比实验，仅验证所提方法重建连续缺失地震数据的有效性。图10显示了分层介质的局部图像。为不失一般性，本文依次从原始图像中提取出11道和22道，然后使用所提出的方法进行重建。连续缺失数据、重建结果和重建误差分别如图11和图12所示。可以看出，两种情况下都能获得较好的重建结果，说明所提方法具有一定的空间表示能力，能够重建有限范围的连续缺失道。

图10 原始剖面Fig.10 Original profile

a—连续缺失11道图像;b—重建结果;c—绝对误差a—11 consecutive missing images;b—reconstruction result;c—absolute error图11 连续缺失11道Shearlet+DCT重建Fig.11 Shearlet+DCT reconstruction of 11 consecutive missing

a—连续缺失22道图像;b—重建结果;c—绝对误差a—22 consecutive missing images;b—reconstruction result;c—absolute error图12 连续缺失22道Shearlet+DCT重建Fig.12 Shearlet+DCT reconstruction of 22 consecutive missing

4 结论及讨论

由于缺道坏道等问题，地震数据往往是不完整的。从反演的角度看，不完整图像重建是一个病态反问题。CS技术利用较少的随机采样数据重构出完整信号，其主要思想是利用信号在某一变换域的稀疏性。

本文在MCA框架下提出了一种新的字典组合:Shearlet+DCT。Shearlet变换是多尺度、多方向的，可以得到更稀疏的系数，DCT是一种用于重建平滑构造的全局型变换。因此，Shearlet+DCT得到的信号系数更加稀疏，无论对局部细节还是整体图像趋势都有很好的重建效果。通过数值实验对Shearlet、DCT和Shearlet+DCT这3种方法进行了比较。结果表明，本文提出方法的重建结果的相对误差较小，可以很好地重建局部细节和深弱反射信号。但随着数据的复杂度的提升，数学变换的局限性会逐渐暴露出来。我们现在也在使用学习算法来训练自适应基函数，以获得更好的结果。

本文还证明了分段随机采样比Jitter采样更有利于数据重建。CS的理论基础是随机采样，但在实际应用中，地震道往往在大范围内连续缺失，难以满足随机采样的假设。对于有限数量的连续缺失案例，本文提出的重建方法也是有效的。但对于大连续缺失区域，例如超过 22 道连续缺失，重建结果并不是很理想。经反复实验，我们得出对于复杂实际资料来说，压缩感知可以接受原始数据10%以内的连续缺失，这一范围随数据量的大小、数据复杂程度及层位密集程度的整加而减小，随三者的降低而增加。因此，下一步的研究重点将是开发大连续缺失信号的空间表达，利用有限的信息进行重建并开发更好的重建方法，如字典学习或机器学习重建方法等。